FC-RRT*: الگوریتم برنامه ریزی مسیر بهبود یافته برای پهپاد در محیط پیچیده سه بعدی

در محیط‌های پیچیده، برنامه‌ریزی مسیر کلید وسایل نقلیه هوایی بدون سرنشین (UAV) برای انجام مأموریت‌های نظامی به صورت مستقل است. این مقاله الگوریتم جدیدی به نام ستاره درخت تصادفی کاوش سریع مبتنی بر هزینه پرواز (FC-RRT*) پیشنهاد می‌کند که ستاره استاندارد درخت تصادفی با کاوش سریع (RRT*) را برای مقابله با الزامات ایمنی و محدودیت‌های پرواز پهپادها در یک مجتمع گسترش می‌دهد. محیط سه بعدی ابتدا، یک تابع هزینه پرواز که شامل قدرت تهدید و طول مسیر است برای ارزیابی جامع ارتباط بین دو گره مسیر طراحی شد. دوم، به منظور حل مشکل برنامه ریزی مسیر پهپاد از قسمت جلویی، تابع هزینه پرواز و محدودیت های پرواز برای الهام بخشیدن به گسترش گره های جدید استفاده شد. سوم، تابع هزینه طراحی شده برای هدایت به روز رسانی گره والد استفاده شد تا به الگوریتم اجازه دهد تهدید و طول مسیر را هنگام ایجاد مسیر در نظر بگیرد. نتایج شبیه سازی و مقایسه نشان می دهد که FC-RRT* به طور موثر بر کاستی های استاندارد RRT* غلبه می کند. FC-RRT* قادر است مسیری بهینه را برنامه ریزی کند که به طور قابل توجهی ایمنی مسیر را بهبود می بخشد و همچنین کوتاه ترین فاصله را حفظ می کند و در عین حال محدودیت های پرواز را در محیط پیچیده برآورده می کند. این مقاله دارای ارزش کاربردی در برنامه ریزی مسیر جهانی سه بعدی پهپاد است. FC-RRT* قادر است مسیری بهینه را برنامه ریزی کند که به طور قابل توجهی ایمنی مسیر را بهبود می بخشد و همچنین کوتاه ترین فاصله را حفظ می کند و در عین حال محدودیت های پرواز را در محیط پیچیده برآورده می کند. این مقاله دارای ارزش کاربردی در برنامه ریزی مسیر جهانی سه بعدی پهپاد است. FC-RRT* قادر است مسیری بهینه را برنامه ریزی کند که به طور قابل توجهی ایمنی مسیر را بهبود می بخشد و همچنین کوتاه ترین فاصله را حفظ می کند و در عین حال محدودیت های پرواز را در محیط پیچیده برآورده می کند. این مقاله دارای ارزش کاربردی در برنامه ریزی مسیر جهانی سه بعدی پهپاد است.

کلید واژه ها:

برنامه ریزی مسیر ؛ ستاره درخت تصادفی در حال کاوش سریع (RRT*) ؛ وسایل نقلیه هوایی بدون سرنشین (UAVs) ؛ الگوریتم های مبتنی بر نمونه برداری

۱٫ مقدمه

در دهه گذشته، وسایل نقلیه هوایی بدون سرنشین (پهپاد) به تدریج نقش مهمی در عملیات های مختلف نظامی ایفا کردند [ ۱ ]. پهپادها می توانند قابلیت دفاع غافلگیر کننده هدف تهدید، قابلیت فرار سریع از میدان نبرد، قابلیت سرکوب آتش خصمانه و قابلیت رزمی متنوع چند بعدی را تا حد زیادی بهبود بخشند. برنامه ریزی مسیر یکی از مهم ترین مشکلاتی است که می تواند در طول پرواز ناوبری خودمختار پهپادها رخ دهد [ ۲ ، ۳ ]، که معمولاً به عنوان یافتن مستقل مسیر بهینه از گره شروع تا گره پایان تعریف می شود [ ۴ ].]. انتخاب مسیر بهینه باید بر اساس محدودیت‌های عملکرد پرواز، الزامات مأموریت خاص، و محدودیت‌های محیط پرواز تعیین شود [ ۵ ، ۶ ]. محققان تحقیقات زیادی در مورد مسئله برنامه‌ریزی مسیر پهپاد انجام داده‌اند و مجموعه‌ای از الگوریتم‌ها، مانند روش‌های بهینه‌سازی مبتنی بر نمودار، از جمله الگوریتم نمودار دید (VG) [ ۷ ] و نمودارهای Voronoi [ ۸ ] را پیشنهاد کرده‌اند. روش های مبتنی بر جستجو، از جمله الگوریتم Dijkstra [ ۹ ]، الگوریتم A* [ ۱۰ ] و الگوریتم D* [ ۱۱ ]. روش‌های مبتنی بر نمونه‌گیری، مانند الگوریتم PRM [ ۱۲ ] و الگوریتم RRT [ ۱۳ ]]؛ روش های الهام گرفته از طبیعت، مانند الگوریتم ژنتیک (GA) [ ۱۴ ]، بهینه سازی کلنی مورچه ها (ACO) [ ۱۵ ]، الگوریتم میدان پتانسیل مصنوعی [ ۱۶ ]، بهینه سازی ازدحام ذرات (PSO) [ ۱۷ ] و الگوریتم مبتنی بر سیال [۱۷] ۱۸ ]; و روش های دیگر، مانند روش های مبتنی بر نظریه کنترل [ ۱۹ ].

به عنوان یک الگوریتم برنامه‌ریزی مسیر مبتنی بر نمونه‌برداری، RRT* به‌طور صریح کل فضای برنامه‌ریزی و مرزهای آن را به عنوان یک روش مبتنی بر جستجو نمی‌سازد، اما در عوض مستقیماً نمونه‌هایی را از طریق نمونه‌گیری برای تشکیل درخت جستجو به دست می‌آورد. این رویکرد از مشکلی که در آن زمان جستجو با تعداد ابعاد فضایی به طور تصاعدی رشد می‌کند، اجتناب می‌کند، بنابراین زمان جستجوی موجود برای برنامه‌ریزی مسیر در فضاهای با ابعاد بالا را به طور قابل‌توجهی کاهش می‌دهد [ ۲۰ ، ۲۱ ]. در همین حال، در مقایسه با روش‌های هوشمند مانند GA و ACO، RRT* دارای پیچیدگی الگوریتمی کمتری در فضای سه‌بعدی است [ ۲۲ ، ۲۳ ]]. به این ترتیب، برای حل مسئله برنامه ریزی مسیر در فضای سه بعدی مناسب تر است. علاوه بر این، RRT* از نظر مجانبی بهینه است. به عبارت دیگر، وقتی تعداد نمونه ها به بی نهایت میل می کند، راه حلی که توسط RRT* به دست می آید، راه حل بهینه ای است که با جواب احتمال همگرا می شود [ ۲۴ ]. بنابراین، برای برنامه ریزی مسیر پهپاد در یک محیط پیچیده، RRT* می تواند اطمینان حاصل کند که یک مسیر امکان پذیر در فضای سه بعدی به سرعت پیدا می شود. به طور خلاصه، RRT* برای برنامه ریزی مسیر پهپاد نسبت به سایر الگوریتم ها در محیط های پیچیده مناسب تر است.

پیشرفت‌های تحقیقاتی اخیر بسیاری از الگوریتم‌های بهبود یافته RRT* را با استفاده از رویکردهای مختلف برای بهبود عملکرد RRT* پیشنهاد کرده‌اند. از یک طرف، برخی از محققان از نمونه گیری بایاس برای بهبود RRT* استفاده می کنند [ ۲۵ ، ۲۶ ، ۲۷ ، ۲۸ ]. این رویکرد تلاش می‌کند تا نمونه‌ها را از طریق روش بایاسینگ در ناحیه مطلوب توزیع کند، مانند تتا*-RRT* [ ۲۷ ] و A*-RRT* [ ۲۸ ].]. اگرچه این رویکرد می تواند کیفیت نمونه برداری اولیه و سرعت همگرایی الگوریتم را بهبود بخشد، مسیر برنامه ریزی نمی تواند محدودیت های پرواز و محیطی پهپاد را برآورده کند. از سوی دیگر، برخی از الگوریتم‌های بهبود یافته RRT* مبتنی بر اطلاعات اکتشافی برای هدایت نمونه‌گیری محلی نیز پیشنهاد شده‌اند [ ۲۹ ، ۳۰ ، ۳۱ ، ۳۲ ]. این الگوریتم‌ها از اطلاعات اکتشافی برای هدایت جستجو پس از اینکه RRT* برای اولین بار یک مسیر عملی را پیدا کرد به منظور یافتن سریع مسیر بهینه استفاده می‌کنند. علاوه بر دو رویکرد بهبودیافته ذکر شده در بالا، رویکرد دیگری وجود دارد که می‌تواند برای بهبود عملکرد RRT* پیاده‌سازی شود که آرامش بهینه مجانبی [ ۳۳ ، ۳۴ ]، ۳۵ ]، مانند از طریق LBT-RRT پیشنهاد شده توسط سالزمن [ ۳۳ ]. مسیری که توسط این الگوریتم به دست می آید در نهایت با احتمال یک به مسیری در ضریب همگرا می شود.

(1 + ε)

از مسیر بهینه، بنابراین مجانبی نزدیک به بهینه نامیده می شود. در مقایسه با RRT، این الگوریتم راه‌حل‌های با کیفیت بالا را سریع‌تر تولید می‌کند و کیفیت راه‌حل‌ها اساساً با راه‌حل‌های RRT* یا RRG قابل مقایسه است. الگوریتم های دیگری که از این رویکرد بهبود یافته استفاده می کنند SST [ ۳۴ ] و NoD-RRT [ ۳۵ ] هستند. این رویکردها می توانند به طور موثر عملکرد RRT* را بهبود بخشند، اما راه حل مجانبی تقریباً بهینه است.

تعیین اینکه الگوریتم‌های RRT* بهبود یافته توسط این سه رویکرد مختلف برای برنامه‌ریزی مسیر پهپاد مناسب نیستند، دشوار نیست زیرا آنها نه تأثیر محیط‌های پیچیده بر ایمنی مسیر پهپادها و نه محدودیت‌های پرواز را در نظر نمی‌گیرند. توجه داشته باشید که در این مقاله، ایمنی مسیر به این موضوع اشاره دارد که چگونه وقتی مسیر پهپاد تحت تأثیر تهدیدات با تشخیص یا محدوده حمله قرار می‌گیرد، مسیر برنامه‌ریزی‌شده این امکان را برای پهپاد فراهم می‌کند تا از تهدید شدن اجتناب کند و ایمنی آن را تضمین کند. اگر ایمنی مسیر و محدودیت های پرواز تعیین شده توسط یک محیط پیچیده پس از ایجاد مسیر بهینه با استفاده از این الگوریتم های بهبودیافته در نظر گرفته شوند، در آن صورت بهینه بودن مسیر نهایی تحت تأثیر قرار می گیرد و ممکن است حتی یک مسیر امکان پذیر نیز پیدا نشود. از این رو، برای برنامه‌ریزی و بهینه‌سازی مسیر پهپاد در محیط‌های پیچیده سه‌بعدی، تأثیر تهدیدات مختلف بر ایمنی مسیر و محدودیت‌های پرواز باید به طور کامل در هنگام یافتن مسیر بهینه در نظر گرفته شود تا اطمینان حاصل شود که مسیر برنامه‌ریزی نهایی، مسیر بهینه‌ای است که هر دو ایمنی را برآورده می‌کند. و محدودیت های پرواز در الگوریتم پراکنده A* [36 ]، نویسندگان محدودیت‌های پرواز را هنگام جستجوی فضا در نظر گرفتند، که امکان دستیابی به یک مسیر بهینه قابل پرواز را فراهم می‌کرد و در عین حال دامنه جستجو و پیچیدگی را بسیار کاهش می‌داد. به طور مشابه، در برخی از الگوریتم‌های تکاملی [ ۳۷ ، ۳۸ ]، تأثیر تهدید محیط پیچیده و محدودیت‌های پرواز نیز در تابع هدف گنجانده شده است تا با برآورده کردن ایمنی و محدودیت‌های مسیر، مستقیماً مسیر بهینه برنامه‌ریزی شود. با این حال، پیشرفت های کمی که برنامه ریزی مسیر پهپاد را در محیط های پیچیده مناسب می کند برای الگوریتم RRT* مشاهده شده است.

برای محدودیت های مکانیک پرواز پهپادها، دو مطالعه، [ ۳۷ ، ۳۹]، برخی از محدودیت های پرواز معمولی را برای برنامه ریزی مسیر پهپاد ارائه می دهد. بیشتر این محدودیت ها در سطح هندسی متمرکز می شوند تا نقاط مسیر را در مسیر برنامه ریزی شده محدود کنند (مانند محدودیت های زاویه پهپاد و غیره). اگر فقط طول مسیر برنامه ریزی شده به عنوان استاندارد برای ارزیابی مسیر استفاده شود، آنگاه این محدودیت ها امکان پذیر هستند. با این حال، در این مقاله، ما باید هزینه تهدید مسیر پهپادها را نیز در نظر بگیریم. ارزیابی هزینه تهدید مسیر تنها با تکیه بر نقاط مسیر امکان پذیر نیست. گاهی اوقات، موقعیت‌هایی پیش می‌آید که نقاط مسیر مجاور محدودیت‌ها را برآورده می‌کنند، اما بخش‌های مسیر اینطور نیستند. بنابراین، این مقاله برخی از بهبودها را در محدودیت های پرواز در [ ۳۷ ، ۳۹ ] ایجاد می کند]. برای برخی از محدودیت‌هایی که باید در بخش مسیر ارزیابی شوند، در نظر بگیرید که آیا قسمت مسیر با محدودیت در تضاد است در حالی که نقطه مسیر با محدودیت مواجه است یا خیر.

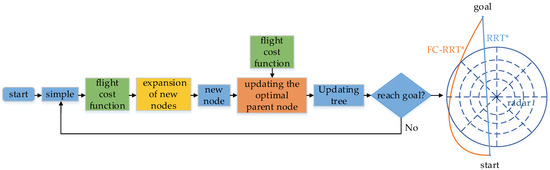
بنابراین، برای مسائل برنامه ریزی مسیر پهپاد در محیط های عملیاتی نظامی پیچیده، این مقاله الگوریتم جدیدی به نام FC-RRT* را پیشنهاد می کند که از A* پراکنده و الگوریتم های تکاملی بهبود یافته الهام گرفته شده است. ما یک تابع هزینه پرواز طراحی کردیم که از هزینه مسافت و هزینه تهدید به عنوان مبنای FC-RRT* استفاده می کند. در گسترش گره های درختی، تابع هزینه پرواز و محدودیت های پرواز را به طور جامع در نظر می گیریم و از آنها به عنوان اطلاعات اکتشافی برای هدایت گسترش گره های درختی استفاده می کنیم. پس از آن، تابع هزینه پرواز و محدودیت های پرواز نیز برای هدایت به روز رسانی گره های والد استفاده می شود. با هدایت تابع هزینه پرواز و محدودیت پرواز با هم دو بار، الگوریتمی برای یافتن یک مسیر بهینه با کوتاه ترین طول ایجاد می شود که ایمنی مسیر و محدودیت های پرواز را برآورده می کند. این مسیر نیازمندی‌های برنامه‌ریزی عملیات نظامی مانند نظارت و شناسایی، قابلیت سرکوب آتش متخاصم، قابلیت فرار سریع از میدان نبرد و قابلیت دفاع غافلگیرانه تهدید-هدف را برآورده می‌کند. مشارکت ها را می توان به شرح زیر خلاصه کردشکل ۱ :

یک تابع هزینه پرواز شامل قدرت تهدید و طول مسیر برای بهبود ایمنی مسیر پهپاد در محیط‌های پیچیده ایجاد شد. ایمنی مسیر یکی از مهمترین الزامات در برنامه ریزی مسیر پهپاد است. بنابراین، قضاوت در مورد مسیر تنها با استفاده از فاصله اقلیدسی اتخاذ نمی شود. با در نظر گرفتن این مشکل، یک تابع هزینه پرواز که شامل طول مسیر و قدرت تهدید است برای هدایت برنامه ریزی مسیر پهپاد پیشنهاد شده است. این امر پهپاد را قادر می سازد تا به طور موثر از تهدیدات جلوگیری کند و با به دست آوردن کوتاه ترین مسیر، ایمنی مسیر خود را بهبود بخشد.
این مقاله رویکردی را برای هدایت گسترش گره‌های جدید با استفاده از اطلاعات اکتشافی پیشنهاد می‌کند. برای حل مشکل قدرت تهدید در برنامه‌ریزی مسیر پهپاد از جلو، هم طول مسیر و هم هزینه استحکام تهدید و همچنین محدودیت‌های پرواز باید در نظر گرفته شود که FC-RRT* توسعه گره جدید را انجام می‌دهد. بنابراین، ما رویکردی را پیشنهاد می‌کنیم که از تابع هزینه پرواز به‌عنوان اطلاعات اکتشافی برای هدایت مستقیم گسترش گره در حالی که برای اولین بار محدودیت‌های پرواز را به آن معرفی می‌کند، استفاده می‌کند. علاوه بر این، ساختار الگوریتم برای بهبود کارایی عملیات FC-RRT* بهینه شده است. با استفاده از این رویکرد، قدرت تهدید مسیر از گسترش اولیه گره جدید کاهش می یابد تا ایمنی مسیر پهپاد تضمین شود. علاوه بر این، FC-RRT* همچنین منجر به پراکندگی نمونه کمتر در فضای برنامه ریزی می شود.
این مقاله یک رویکرد جدید برای به‌روزرسانی گره والد بهینه در منطقه همسایه پیشنهاد می‌کند. پس از اینکه گره جدید توسط تابع هزینه پرواز و محدودیت های پرواز هدایت شد، رویکردی برای معرفی تابع هزینه پرواز و محدودیت های پرواز برای به روز رسانی گره والد برای هدایت یافتن مسیر بهینه پیشنهاد شده است. این رویکرد گره‌های والد را با کوتاه‌ترین طول مسیر انتخاب می‌کند و می‌تواند به طور موثری از تهدیدات هنگام به‌روزرسانی گره والد جلوگیری کند تا از کشف شدن توسط دشمن یا برخورد با موانع و اطمینان از ایمنی مسیر جلوگیری شود.

بقیه این مقاله به شرح زیر سازماندهی شده است: بخش ۲ برنامه ریزی مسیر پهپاد در محیط های پیچیده را توصیف می کند که پایه و اساس کار فعلی را می گذارد. بخش ۳ الگوریتم FC-RRT* را به تفصیل از پنج جنبه تجزیه و تحلیل می کند: چارچوب FC-RRT*. تعیین تابع هزینه پرواز؛ معیارهای ارزیابی مسیر؛ رویکرد انتخاب گره جدید، که توسط اطلاعات اکتشافی هدایت می شود. و رویکرد به روز رسانی گره والد بهبود یافته است. بخش ۴ FC-RRT*، از جمله کامل بودن احتمالی و بهینه مجانبی آن را تحلیل می‌کند و پیچیدگی محاسباتی مجانبی آن را با RRT* مقایسه می‌کند. نتایج شبیه سازی و مقایسه در بخش ۵ مورد بحث قرار گرفته است. بخش ۶شامل نتیجه گیری و چشم انداز آینده است.

۲٫ شرح کار و مشکل مرتبط

ما به طور خلاصه الگوریتم A*، الگوریتم RRT و الگوریتم RRT* را به عنوان شرح کار مربوطه در بخش ۲٫۱ خلاصه می کنیم . سپس، مشکلاتی که در این مقاله توضیح داده می شود، در بخش ۲٫۲ مورد تجزیه و تحلیل و بحث قرار می گیرند .

۲٫۱٫ کار مرتبط

الگوریتم A* یک الگوریتم کلاسیک جستجوی کوتاه ترین مسیر است که بر اساس الگوریتم Dijkstra است. جهت جستجو با معرفی اطلاعات اکتشافی فاصله از گره تا نقطه پایانی در فرآیند گسترش گره به منظور بهبود کارایی جستجو و کوتاه کردن زمان جستجو تعیین می‌شود. الگوریتم A* امکان آن گره را اندازه گیری می کند

n

نقطه ای در کوتاه ترین مسیر است که از طریق یک تابع تخمین تعیین می شود

f (n)

در طول گسترش گره تابع ارزش گذاری

f (n)

را می توان به صورت بیان کرد

f (n) = g (n) + h (n)

، جایی که

g (n)

نشان دهنده هزینه واقعی از گره اولیه به گره است

n

، و

h (n)

هزینه برآورد شده از گره n تا گره هدف را نشان می دهد. از آنجایی که عبارت اکتشافی به گره هدف مربوط می شود، جهت جستجوی گره در الگوریتم A* به منظور بهبود کارایی جستجو به نقطه هدف هدایت می شود.

الگوریتم RRT نقطه شروع را به عنوان گره ریشه می گیرد و یک درخت جستجوی سریع متشکل از بخش های مسیر امکان پذیر را به صورت تدریجی می سازد. در ابتدای الگوریتم، یک درخت جستجو تنها با استفاده از گره اولیه به عنوان گره ریشه ساخته می شود. اول، نقطه هدف گسترش

x_{r a n d}

با نمونه گیری تصادفی، و سپس، گره برگ تعیین می شود

x_{n e a r e s t}

نزدیکترین به

x_{r a n d}

از گره های درخت فعلی یافت می شود. اگر فاصله بین

x_{r a n d}

x_{n e a r e s t}

پس در محدوده خاصی قرار دارد

x_{r a n d}

به عنوان گره جدید گرفته می شود

x_{n e w}

; در غیر این صورت، یک گره را در محدوده مشخصی در اطراف گره برگ انتخاب کنید

x_{r a n d}

جهت بودن

x_{n e w}

. سپس، سعی کنید وصل شوید

x_{n e w}

به درخت اگر ارتباط بین

x_{n e w}

x_{n e a r e s t}

با موانع محیطی برخورد نمی کند، وصل شوید

x_{n e w}

در درخت جستجو به عنوان یک گره برگ جدید. هنگامی که گره برگ درخت تصادفی حاوی هدف است یا در ناحیه اطراف هدف قرار دارد، مسیری از ابتدا تا هدف که از گره های درختی تشکیل شده است در درخت تصادفی یافت می شود.

در مقایسه با الگوریتم RRT *، الگوریتم RRT فرآیند بهینه سازی را هنگام اتصال نقاط نمونه گیری در طول درخت جستجو افزایش می دهد. روش انتخاب گره والد برای

x_{n e w}

به شرح زیر است: مجموعه را پیدا کنید

X_{n e a r}

از همه گره ها

x_{n e a r}

در فاصله معینی از

x_{n e w}

و سپس نقطه in را انتخاب کنید

X_{n e a r}

که می توان با آن ارتباط برقرار کرد

x_{n e a r}

بدون برخورد و کوتاه ترین طول را به عنوان گره والد دارد. سپس،

x_{n e a r}

نزدیک

x_{n e w}

در درخت بررسی می شود. زمانی که مسیر از

x_{n e a r}

به

x_{n e w}

کوتاه تر است، ارتباط بین را حذف کنید

x_{n e a r}

و گره والد، و گره والد این نقاط را به عنوان نقطه تنظیم کنید

x_{n e w}

۲٫۲٫ شرح مشکل

در محیط‌های پرواز واقعی که پهپادها در حال انجام عملیات نظامی هستند، معمولاً انواع مختلفی از موانع و تهدیدها از جمله تهدیدات زمین، تهدیدات راداری، تهدیدات ضد هوایی و تهدیدات منطقه پرواز ممنوع وجود خواهد داشت. انواع مختلف تهدیدها به روش های مختلف مدیریت می شوند. بنابراین، این مقاله به منظور بازیابی واقعی محیط پرواز پهپاد، یک محیط پیچیده حاوی تهدیدات فوق را شبیه سازی کرده و مسیر پهپاد را در این محیط برنامه ریزی می کند. تعریف محیط پیچیده در این مقاله به شرح زیر است:

تعریف ۱ (محیط پیچیده )

. اگر محیطی که برنامه ریزی مسیر پهپاد در آن صورت می گیرد فضایی سه بعدی با تهدیدات زمین، تهدیدات راداری، تهدیدات ضد هوایی و موانع منطقه پرواز ممنوع باشد و همین نوع تهدید بارها رخ دهد، پهپاد محیط برنامه ریزی مسیر به عنوان پیچیده بودن تعریف می شود .

تعریف و مدل سازی انواع موانع در یک فضای پیچیده نیز متفاوت است. در زیر تحلیل می شوند:

(۱) تهدیدات زمین: به دلیل تسکین توپوگرافی بزرگ، اگر تقریباً با پیکربندی اولیه نشان داده شود، اطلاعات بیشتری از دست خواهند رفت. به این ترتیب، نمایش این اطلاعات توپوگرافی با استفاده از پیکربندی اولیه دشوار است. به منظور نمایش دقیق اطلاعات زمین و بهبود کارایی عملیات، توجه می‌کنیم که داده‌های ارتفاعی عمدتاً در شبکه ذخیره می‌شوند، بنابراین تبدیل داده‌های ارتفاعی به یک مدل محیط شبکه سه‌بعدی آسان است. بنابراین، این مقاله از اطلاعات نقشه ارتفاعی جزیره هاوایی به عنوان تهدید زمین استفاده می کند.

(۲) تهدیدات راداری و تهدیدات ضد هوایی: تهدیدات راداری و تهدیدات ضد هوایی را نمی توان به عنوان منطقه پرواز ممنوع تلقی کرد. این به این دلیل است که تهدیدات رادار و ضد هوایی هم برد تشخیص و هم برد حمله دارند. اجتناب از خود تهدید، که خطرات پنهانی را برای امنیت مسیر به همراه خواهد داشت، کافی نیست. بنابراین، هنگام اجتناب از چنین تهدیداتی، همچنین لازم است تا حد امکان از مرکز درمان دور بمانید تا درجه تهدیدی که یک پهپاد در هنگام عبور از محدوده تشخیص رادار یا محدوده حمله ضد هوایی تجربه می کند و کاهش یابد. ایمنی مسیر پهپاد را تا حدی تضمین کنید.

(۳) موانع منطقه پرواز ممنوع: برای جلوگیری از موانع در منطقه پرواز ممنوع، موانع برج را شبیه سازی کردیم. برای چنین موانعی، اگر یک پهپاد مسیری را طراحی کرده باشد که به آن امکان می دهد با موفقیت از برخورد با آنها اجتناب کند، در این صورت پهپاد با موفقیت از چنین موانعی اجتناب کرده است.

این شرایط پیچیده محیطی و عملکرد پهپاد، محدودیت های پروازی زیادی را برای برنامه ریزی مسیر ایجاد می کند. نگاهی دقیق به محدودیت‌های مسائل برنامه‌ریزی مسیر پهپاد نشان می‌دهد که اکثر آنها در سطح هندسی با استفاده از نقاط مسیر مجزا محدود می‌شوند (برنامه‌ریزی مسیر عموماً محدودیت‌های دینامیکی را در نظر نمی‌گیرد). از آنجایی که این مقاله به جای ایجاد محدودیت‌های پروازی جدید، بر مسئله برنامه‌ریزی مسیر پهپاد متمرکز است، ما مستقیماً مجموعه‌ای از محدودیت‌های پروازی مناسب برای این مقاله را بر اساس محدودیت‌های نماینده موجود در [ ۳۷ ، ۳۹ ] انتخاب و استخراج می‌کنیم تا محدودیت‌های عملکرد کلیدی و الزامات محیطی پیچیده در برنامه ریزی مسیر پهپاد

محدودیت ها به صورت زیر محاسبه می شوند.

۱٫: محدودیت طول مسیر

طول مسیر برای نشان دادن فاصله پرواز پهپاد استفاده می شود. اجازه دهید $L_{\max}$ حداکثر فاصله پرواز پهپاد باشد. سپس، محدودیت طول مسیر به صورت محاسبه می شود

f L = \sum i = ۰ ن (ایکس من + ۱ - ایکس من) ۲ + (y من + ۱ - y من) ۲ + (z من + ۱ - z من) ۲ ——————————-\sqrt \leq L حداکثر

(۱)

جایی که $(x_{i}, y_{i}, z_{i})$ ، $i = 1, 2, \dots, N$ ، نشان دهنده مختصات است $i$ -مین نقطه مسیر در محیط برنامه ریزی سه بعدی و $N$ تعداد کل نقاط مسیر است.

۲٫: محدودیت زاویه چرخش

صافی مسیر را در نظر بگیرید، جایی که حداکثر زاویه چرخش است $ϕ_{\max}$ برای محدود کردن زاویه چرخش معرفی شده است. فرض کنید بردار $a_{i}$ برابر است با ${[x_{i} - x_{i - 1}, y_{i} - y_{i - 1},]}^{T}$ ، و $| | a_{i} | |$ هنجار بردار است $a_{i}$ . محدودیت زاویه چرخش پهپاد است

ϕ من = آرکوس (آ تی من آ من + ۱ | | آ من | | | | آ من + ۱ | |) \leq ϕ حداکثر

(۲)

۳٫: محدودیت زاویه صعود/سرخوردن

مشابه زاویه چرخش، زاویه صعود/سرخوردن را می توان به صورت محاسبه کرد

- γ حداکثر \leq γ من = آرکتان (z من - z من - ۱ | | آ من | |) \leq γ حداکثر ،

(۳)

جایی که $γ_{\max}$ حداکثر زاویه صعود است و $- γ_{\max}$ حداقل زاویه سر خوردن است.

۴٫: محدودیت بخش مسیر

پهپاد باید قبل از تغییر وضعیت پرواز یا بعد از چرخش فاصله مستقیم خود را حفظ کند. علاوه بر این، پهپادها معمولاً انتظار ندارند که به طور مکرر بچرخند تا خطاهای ناوبری را کاهش دهند. بنابراین، لازم است که قطعات مسیر بین نقاط مسیر مجاور، بزرگتر از طول قطعه کوتاه‌ترین مسیر باشد. $l_{\min}$ . محدودیت قطعه مسیر را می توان با بیان کرد

ل دقیقه - | | پ من + ۱ - پ من | | \leq ۰ ،

(۴)

جایی که $p_{i + 1}$ است $(x_{i + 1}, y_{i + 1}, z_{i + 1})$ ، و $p_{i}$ است $(x_{i}, y_{i}, z_{i})$ . $p_{i + 1}$ و $p_{i}$ دو نقطه مسیر مجاور هستند.

۵٫: محدودیت زمین

برای محاسبه محدودیت های زمین، تکیه بر نقاط مسیر به تنهایی ممکن است باعث شود که بخش های مسیر مربوطه با زمین برخورد کنند، بنابراین محدودیت های بخش های مسیر نیز باید در نظر گرفته شود. از این رو، اجازه دهید $p_{i, k}$ هر نقطه مسیر در قطعه مسیر باشد $(p_{i}, p_{i + 1})$ ; $H_{s a f e}$ حداقل ارتفاع پرواز ایمن پهپاد است و $z_{i, j}^{m a p}$ ارتفاع زمین در نقطه مسیر است $p_{i, k}$ . سپس، محدودیت زمین است

g 1 ، j = {۰ پ من ، ج \geq اچ s a f ه + z m a p من ، ج ۱ در غیر این صورت

(۵)

ما معمولاً از طول مسیر به عنوان تابع هزینه برای ارزیابی مسیرهای برنامه ریزی شده استفاده می کنیم. اما در این مقاله که تاثیر عوامل محیطی پیچیده بر ایمنی مسیر پهپاد را در نظر می گیرد، فاصله بین مسیر و منطقه تهدید نیز در نظر گرفته شده است تا از برنامه ریزی مسیری بسیار نزدیک به تهدید جلوگیری شود که بیان می شود. از طریق تابع هزینه قدرت تهدید مسیر. در بخش ۳ ، تابع هزینه را به تفصیل تحلیل خواهیم کرد.

۳٫ الگوریتم FC-RRT*

RRT* استاندارد فضای جستجو را با نمونه گیری تقریب می زند و از افزایش شدید پیچیدگی محاسباتی ناشی از افزایش ابعاد فضای جستجو جلوگیری می کند. بنابراین برای برنامه ریزی مسیر پهپاد مناسب است. با این حال، مطالعات [ ۴۰ ، ۴۱ ] ثابت کردند که استاندارد RRT* نمی تواند ایمنی مسیر پهپادها را در برنامه ریزی مسیر تضمین کند و حتی ممکن است مسیر را به دلیل نقض محدودیت های پرواز غیرممکن کند.

بنابراین با توجه به ایمنی مسیر و محدودیت های پرواز پهپادها در محیط های پیچیده، الگوریتم جدیدی به نام FC-RRT* در این مقاله برای یافتن مسیر بهینه پهپاد پیشنهاد شده است. در مرحله اول، یک تابع هزینه پرواز با استفاده از قدرت تهدید و طول مسیر طراحی شده است. در مرحله دوم، تابع هزینه پرواز طراحی شده و محدودیت پرواز برای هدایت مستقیم گسترش گره های جدید استفاده می شود. در نهایت، تابع هزینه پرواز طراحی شده و محدودیت پرواز برای هدایت به روز رسانی گره های مادر در مناطق همسایه استفاده می شود. FC-RRT* قدرت تهدید و طول مسیر را همزمان در نظر می گیرد. هدف آن برنامه ریزی یک مسیر بهینه است که تا حد امکان کوتاه باشد و در عین حال به طور موثر از تهدید جلوگیری کند.

الگوریتم ۱: FC-RRT*

\begin{array}{l} 1 : Notation : Tree T, Enviroment ξ \\ 2 : T . V \leftarrow {p_{s t a r t}}; E \leftarrow \emptyset; \\ 3 : for i = 1 to n do \\ 4 : T \leftarrow (V, E); \\ 5 : p_{r a n d} \leftarrow Sample (ξ); \\ 6 : p_{n e w} \leftarrow Heuristic_\cos t (T . V, p_{r a n d}) \\ 7 : T . V \leftarrow T . V \cup {p_{n e w}}; \\ 8 : P_{n e a r} \leftarrow Near (p_{n e w}, T . V, r_{i}); \\ 9 : for a l l p_{n e a r} \in P_{n e a r} do \\ 10 : rewire_ImpRRT * (p_{n e a r}, p_{n e w}); \\ 11 : for a l l p_{n e a r} \in P_{n e a r} do \\ 12 : rewire_ImpRRT * (p_{n e w}, p_{n e a r}); \\ 13 : return T = (V, E) \end{array}

FC-RRT* همانطور که در الگوریتم ۱ ارائه شده است با RRT* استاندارد در دو بخش متفاوت است: گسترش گره های جدید و به روز رسانی گره های والد در مناطق مجاور. برای گسترش گره جدید، RRT * ابتدا گره ای را در درخت که نزدیک ترین گره به گره نمونه است انتخاب می کند. سپس، یک گره جدید در جهت گره درخت به گره نمونه با توجه به فاصله گسترش انتخاب می شود. در نهایت، اگر گره جدید بدون برخورد باشد، به درخت اضافه می شود [ ۲۴]. در مقابل، الگوریتم FC-RRT* ما از تابع هزینه پرواز به عنوان اطلاعات اکتشافی برای هدایت گسترش گره های جدید استفاده می کند. اطلاعات اکتشافی از قبل شامل راهنمایی در مورد جهت گسترش و فاصله گره های جدید است، بنابراین گره های جدیدی که محدودیت پرواز را برآورده می کنند می توانند مستقیماً به درخت اضافه شوند (الگوریتم ۱، خطوط ۶، ۷). برای به روز رسانی گره والد، معمولاً از فاصله اقلیدسی برای انتخاب نزدیکترین گره والد بدون در نظر گرفتن قدرت تهدید و محدودیت های پرواز در RRT* استفاده می شود. در الگوریتم FC-RRT*، از تابع هزینه پرواز و محدودیت های پرواز برای هدایت انتخاب گره والد بهینه استفاده می کنیم (الگوریتم ۱، خطوط ۹-۱۲). از آنجایی که این رویکرد قدرت تهدید، طول مسیر و محدودیت های پرواز را به طور همزمان در نظر می گیرد، مسیر برنامه ریزی شده یک مسیر بهینه است که ایمنی و محدودیت های مسیر را برآورده می کند.

۳٫۱٫ ارزیابی تابع هزینه پرواز

برای برنامه ریزی مسیر پهپاد در یک محیط پیچیده، تنها در نظر گرفتن یک فاکتور طول مسیر کافی نیست. پهپادها نه تنها هنگام پرواز در میدان نبرد باید از منطقه پرواز ممنوع اجتناب کنند، بلکه باید با توجه به ماموریت های مختلف، تا حد امکان از برخورد تهدیداتی مانند رادارها و توپ های ضد هوایی نیز اجتناب کنند. علاوه بر این، حتی اگر از رادارها و اسلحه های ضدهوایی اجتناب شود، پهپاد همچنان توسط شناسایی راداری و حملات ضد هوایی تهدید می شود، به این معنی که ایمنی مسیر آن را نمی توان تضمین کرد. به عبارت دیگر، ما انتظار داریم الگوریتم این پهپاد را از تهدیدات دور نگه دارد و در عین حال مسیر کوتاه‌تری را به دست آورد تا از کاهش ایمنی مسیر پهپاد تنها با پیگیری کوتاه‌ترین مسیر برنامه‌ریزی شده جلوگیری شود.

به طور کلی، شعاع تهدید اسلحه‌های رادار و ضدهوایی بسیار زیاد است، بنابراین تلاش برای اجتناب کامل از همه تهدیداتی که آنها ایجاد می‌کنند، غیرعملی است. اگر الگوریتم به گونه ای طراحی شده باشد که کاملاً از این تهدیدات عاری باشد، در این صورت طول مسیر افزایش می یابد یا منجر به ایجاد مسیری بسیار فراتر از محیط پرواز می شود. بنابراین، ما نمی توانیم به سادگی این مناطق تهدید را به عنوان مناطق پرواز ممنوع تلقی کنیم که می توان به طور کامل از آنها اجتناب کرد. توجه داشته باشید که با افزایش فاصله پهپاد از پهپاد، احتمال شناسایی توسط رادار و حمله ضد هوایی کاهش می یابد. بنابراین لازم است تاثیر طول مسیر و تهدید مسیر را همزمان در نظر گرفت. به علاوه، تاثیر تهدید مسیر بر تکمیل ماموریت با توجه به ماموریت های مختلف پهپاد به طور مناسب تنظیم می شود. از این رو، متفاوت از تابع هزینه استاندارد RRT*، الگوریتم FC-RRT* روش ارزیابی مسیر اصلی را با استفاده از طول به عنوان تنها هزینه بهبود می بخشد. در این مقاله، ما یک تابع هزینه پرواز با هزینه تهدید و طول بخش‌های مسیر طراحی کردیم که می‌توان از آن برای هدایت گسترش گره‌های جدید و به‌روزرسانی گره‌های والد استفاده کرد. این مسیر برنامه ریزی شده را قادر می سازد تا الزامات مسیر پهپاد را در محیط های پیچیده برآورده کند. تابع هزینه پرواز در این بخش مورد تجزیه و تحلیل قرار می گیرد که پایه و اساس تحلیل الگوریتم بعدی را می گذارد. الگوریتم FC-RRT* با استفاده از طول به عنوان تنها هزینه، روش ارزیابی مسیر اصلی را بهبود می بخشد. در این مقاله، ما یک تابع هزینه پرواز با هزینه تهدید و طول بخش‌های مسیر طراحی کردیم که می‌توان از آن برای هدایت گسترش گره‌های جدید و به‌روزرسانی گره‌های والد استفاده کرد. این مسیر برنامه ریزی شده را قادر می سازد تا الزامات مسیر پهپاد را در محیط های پیچیده برآورده کند. تابع هزینه پرواز در این بخش مورد تجزیه و تحلیل قرار می گیرد که پایه و اساس تحلیل الگوریتم بعدی را می گذارد. الگوریتم FC-RRT* با استفاده از طول به عنوان تنها هزینه، روش ارزیابی مسیر اصلی را بهبود می بخشد. در این مقاله، ما یک تابع هزینه پرواز با هزینه تهدید و طول بخش‌های مسیر طراحی کردیم که می‌توان از آن برای هدایت گسترش گره‌های جدید و به‌روزرسانی گره‌های والد استفاده کرد. این مسیر برنامه ریزی شده را قادر می سازد تا الزامات مسیر پهپاد را در محیط های پیچیده برآورده کند. تابع هزینه پرواز در این بخش مورد تجزیه و تحلیل قرار می گیرد که پایه و اساس تحلیل الگوریتم بعدی را می گذارد.

تابع هزینه پرواز شامل هزینه طول مسیر و هزینه قدرت تهدید است که به صورت تعریف شده است

f ج = λ ل f ل + λ تی f تی ،

(۶)

جایی که $f_{l}$ هزینه طول قطعه مسیر است و $f_{t}$ هزینه تهدید بخش مسیر است. $λ_{l}$ و $λ_{t}$ عوامل وزنی هستند.

۳٫۱٫۱٫ تابع هزینه طول مسیر

برای محاسبه هزینه طول بخش مسیر، اجازه دهید هر جفت گره باشد $p_{a} = (x_{a}, y_{a}, z_{a})$ و $p_{b} = (x_{b}, y_{b}, z_{b})$ . طول $l$ از بخش مسیر $(p_{a}, p_{b})$ است

l = (x a - x b) 2 + (y a - y b) 2 + (z a - z b) 2 ----------------------------\sqrt

(۷)

سپس، تابع هزینه طول $f_{l}$ از بخش مسیر $(p_{a}, p_{b})$ به عنوان … تعریف شده است

f l (p a, p b) = l - l min l max - l min,

(۸)

جایی که $l_{\max}$ حداکثر فاصله بین تمام بخش های مسیر اختیاری است. به همین ترتیب، $l_{\min}$ حداقل فاصله بین بخش های مسیر اختیاری است.

۳٫۱٫۲٫ تابع هزینه قدرت تهدید مسیر

هزینه تهدید میزانی است که پهپاد در حین پرواز در معرض تهدیدات دشمن قرار می گیرد. بدیهی است که هرچه پهپاد به تهدیداتی مانند رادار و ضدهوایی نزدیکتر باشد، احتمال پیدا شدن یا انهدام پهپاد بیشتر می شود، به این معنی که ضربه تهدید قوی تر است. با توجه به محاسبه قدرت تهدید، نه تنها باید شدت تهدید در نقاط مسیر محاسبه شود، بلکه بخش های مسیری که توسط نقاط مسیر به هم متصل می شوند نیز باید به طور تقریبی تحلیل شوند. بنابراین ابتدا قطعه مسیر را به صورت زیر پردازش کردیم.

برای یک بخش مسیر $(p_{a}, p_{b})$ ، آن را به $N_{0}$ قطعات به صورت یکنواخت فرض کنید که $j$ نقطه تقسیم در بخش مسیر $(p_{a}, p_{b})$ به عنوان مشخص می شود $p_{a b, j} = (x_{a b, j}, y_{a b, j}, z_{a b, j})$ ، که به صورت محاسبه می شود

p a b, j = p b - p a N 0 j + p a

(۹)

تعیین $N_{0}$ مقدار به حداقل شعاع تهدید و حداقل قطر تقریبی زمین تپه بستگی دارد. لازم است اطمینان حاصل شود که طول تمام بخش های تقسیم کننده کمتر از حداقل قطر رادار، اسلحه های ضد هوایی و سایر تهدیدات باشد. با این کار مشخص می‌شود که آیا بخش مسیر با تهدیدها در تضاد است یا خیر، و هیچ موقعیتی وجود نخواهد داشت که نقاط مسیر محدودیت را برآورده کنند، اما بخش مسیر چنین نیست. $N_{0}$ به عنوان محاسبه می شود

min N 0 = ⌈ f L 2 N min ( r 1 , \dots r n ) ⌉,

(۱۰)

جایی که $N$ تعداد بخش های مسیر است و $r_{1}, \dots, r_{n}$ حداقل شعاع است $n$ تهدیدات یا زمین تپه ای $f_{L}$ طول کل مسیر است که تقریباً ۱٫۵ تا ۲ برابر فاصله شروع تا مقصد است. $N_{0}$ همچنین پس از برآورده شدن محدودیت مقدار حداقل، می توان با توجه به نیاز دقت افزایش داد. با این حال، باید توجه داشت که هر چه بزرگتر باشد $N_{0}$ است، پیچیدگی محاسباتی بالاتر خواهد بود.

برای یک بخش مسیر $(p_{a}, p_{b})$ که به طور مساوی تقسیم می شود $N_{0}$ بخش‌ها، شدت تهدید را می‌توان به صورت بیان کرد

t = ( x a - x b ) 2 + ( y a - y b ) 2 + ( z a - z b ) 2 ----------------------------\sqrt N 0 \sum k K \sum j N 0 + 1 1 d j , k

(۱۱)

از این رو، تابع هزینه تهدید است

f t (p a, p b) = t - t min t max - t min,

(۱۲)

با

d j, k = {∣∣ ∣∣ [p b - p a N 0 (j - ۱) + p a] - R k ∣∣ ∣∣ - r k d j, k \leq L t h \infty otherwise,

(۱۳)

جایی که $L_{t h}$ محدوده تاثیر تهدیدات را نشان می دهد، $k = 1, 2, \dots, K$ را نشان می دهد $K$ تهدیدات در محدوده تاثیر، $t_{\max}$ و $t_{\min}$ به ترتیب حداکثر قدرت تهدید و حداقل قدرت تهدید در بین تمام بخش‌های مسیر اختیاری هستند. $d_{j, k}$ کوتاه ترین فاصله بین $k$ تهدید و نقطه تقسیم، $R_{k}$ مرکز تهدید است و $r_{k}$ شعاع تهدید است. $r_{k}$ برای تهدیدهای مختلف کمی متفاوت محاسبه می شود. بنابراین، ما باید نزدیکترین فاصله را برای مدل های مختلف تهدید موجود در این مقاله به طور جداگانه محاسبه کنیم.

۳٫۲٫ ارزیابی مسیر بر اساس تابع هزینه پرواز

هدف از الگوریتم پیشنهادی یافتن یک مسیر بهینه مناسب برای یک پهپاد است. تابع هزینه پرواز طراحی شده برای ارزیابی کیفیت مسیر استفاده خواهد شد. تعریف مسیر بهینه در FC-RRT* به شرح زیر است:

تعریف ۲٫

برای هر گروه وزنه $[λ_{l}, λ_{t}] : λ_{l} + λ_{t} = 1$ هنگامی که هزینه کل پرواز A هر بخش مسیر کوچکترین باشد، مسیر برنامه ریزی شده به عنوان مسیر بهینه در نظر گرفته می شود، به عنوان مثال،

σ o p t i m a l : [پ ۰ ، پ ۱ \dots پ ن] = \cup i = ۰ ن arg min f ج ([پ من ، پ من + ۱]) ،

(۱۴)

جایی که $σ_{o p t i m a l}$ نشان دهنده مسیر بهینه است که از آن تشکیل شده است $N + 1$ نقاط مسیر $[p_{0}, p_{1} \dots p_{N}]$ .

برای تخصیص اوزان

λ_{l}

λ_{t}

، تهدید مسیر و طول مسیر را می توان با توجه به وظایف مختلف اولویت بندی کرد:

نفوذ و فرار سریع. اگر پهپاد برای انجام کار مورد نیاز باشد، نشان می دهد که کاربر انتظار دارد مسیر کوتاه تری را برای رسیدن سریع به هدف به دست آورد. در این زمان، وزن طول مسیر موقعیت غالب را اشغال می کند و تاثیر تهدید مسیر را ضعیف می کند.
حمله سریع تحت این نوع کار، پهپاد باید توانایی خاصی برای اطمینان از ایمنی خود داشته باشد. در عین حال، با فرض خطر نسبتاً کوچک، پهپاد باید به سرعت به اهداف دشمن حمله کند. بنابراین لازم است مسیر برنامه ریزی شده عملکرد امنیتی خاصی را نشان دهد و مسیر را تا حد امکان کوتاه کند. به عبارت دیگر، الزامات خاصی برای تهدیدات و طول مسیر وجود دارد.
شناسایی و گشت زنی. از آنجایی که اجرای این نوع ماموریت نیاز به اطمینان از ایمنی مسیر پهپاد و همچنین عدم یافتن آن توسط دشمن در هنگام شناسایی دارد، تاثیر تهدید مسیر از اهمیت ویژه ای برخوردار است. بخش ۵ این مقاله به تجزیه و تحلیل برنامه ریزی مسیر تحت وظایف مختلف از طریق شبیه سازی می پردازد.

۳٫۳٫ پسوند نود جدید بر اساس اطلاعات اکتشافی

استاندارد RRT* نقطه ای را پیدا می کند که نزدیک ترین نقطه به آن است

p_{r a n d}

در درخت با محاسبه فاصله اقلیدسی و سپس گسترش گره جدید

p_{n e w}

از طریق برنامه ریز محلی [ ۲۴ ]. این رویکرد جدید گسترش گره برای برنامه ریزی مسیر پهپاد مناسب نیست. در عملیات نظامی، محیط های پروازی که در آن از پهپادها استفاده می شود، پیچیده است. به منظور به حداقل رساندن احتمال تحت تاثیر قرار گرفتن یک پهپاد توسط تهدیدات یا برخورد با موانع، گره ای که می تواند به طور موثر از تهدید جلوگیری کند و کمترین فاصله را از گره درخت داشته باشد تا حد امکان انتخاب می شود. در این میان محدودیت های پروازی نیز باید در نظر گرفته شود. بنابراین در FC-RRT* از تابع هزینه پرواز طراحی شده استفاده می کنیم

f_{c}

برای الهام بخشیدن به گسترش گره های جدید و معرفی محدودیت های پرواز برای غربالگری گره های جدید.

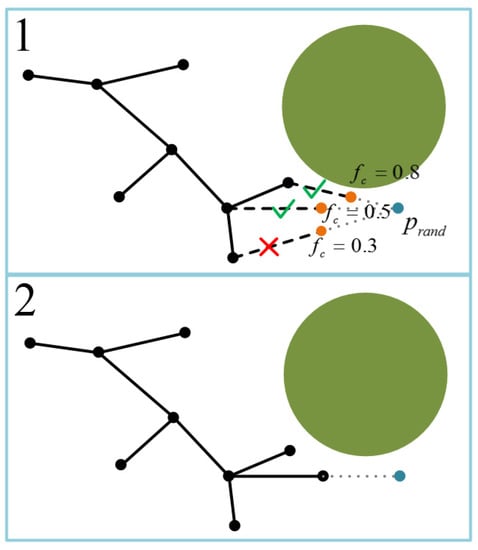
همانطور که در شکل ۲ نشان داده شده است ، پس از به دست آوردن گره نمونه

p_{r a n d}

، ما استفاده می کنیم

Heuristic_\cos t ()

برای برگرداندن گره جدید

p_{n e w}

. فرآیند اطلاعات اکتشافی برای هدایت گسترش گره جدید در الگوریتم ۲ نشان داده شده است. ابتدا، فواصل اقلیدسی بین هر گره درختی

p_{v}

p_{r a n d}

جداگانه محاسبه می شوند. اگر فاصله بین گره های درختی

p_{v}

p_{r a n d}

کمتر از حداکثر فاصله توسعه یافته ارائه شده توسط FC-RRT* و بزرگتر از فاصله محدودیت قطعه کوتاه ترین مسیر است.

l_{\min}

، سپس

p_{r a n d}

به عنوان یک گره جدید بالقوه تعیین می شود. اگر این فاصله بیشتر از

l_{\min}

، سپس راس با افزایش طول ایجاد می شود

δ

در امتداد گره درخت

p_{v}

در مسیر

p_{v}

به

p_{r a n d}

به عنوان یک گره جدید بالقوه محاسبه می شود.

الگوریتم ۲:

Heuristic_\cos t (T . V, p_{r a n d})

\begin{array}{l} 1 : for a l l p_{v} \in T . V do \\ 2 : if (l_{\min} \leq ∥ p_{v} - p_{r a n d} ∥ \leq δ) \\ 3 : p_{n e w} \leftarrow p_{r a n d} \\ 4 : elseif (∥ p_{v} - p_{r a n d} ∥ > δ) \\ 5 : p_{n e w} \leftarrow p_{v} + δ \frac{p_{r a n d} - p_{v}}{∥ p_{r a n d} - p_{v} ∥} \\ 6 : if (collision_free (p_{v}, p_{n e w}) \land \\ UAV_free (p_{v}, p_{n e w})) then \\ 6 : c \leftarrow λ_{l} f_{l} (p_{v}, p_{r a n d}) + λ_{t} f_{t} (p_{v}, p_{n e w}) \\ 7 : else \\ 8 : continue \\ 9 : p_{n e w} \leftarrow argmin (c) \end{array}

سپس، محدودیت‌های محیطی و محدودیت‌های پرواز برای لبه بالقوه شناسایی می‌شوند

(p_{v}, p_{n e w})

. ما استفاده می کنیم

collision_free ()

برای تشخیص برخورد با تهدیدات و زمین. علاوه بر این، ما استفاده می کنیم

UAV_free ()

برای تشخیص اینکه آیا مسیر برنامه ریزی شده زاویه چرخش و محدودیت های زاویه صعود/سرخوردن را برآورده می کند یا خیر.

اگر هر دو محدودیت برآورده شوند، از تابع هزینه پرواز طراحی شده برای محاسبه هزینه بین گره جدید بالقوه و هر گره درخت استفاده می شود.

p_{v}

. فاصله اقلیدسی بین گره نمونه

p_{r a n d}

و هر گره درخت

p_{v}

به طور مستقیم برای تعیین هزینه طول مسیر محاسبه می شود

f_{l}

. با این حال، برای محاسبه هزینه قدرت تهدید

f_{t}

، به دلیل محدودیت حداکثر طول گسترش

δ

، گره جدید فقط در محدوده تعیین می شود

δ

اطراف گره درخت بنابراین برای ارزیابی صحیح قدرت تهدید، لبه متشکل از

p_{v}

و هر گره جدید بالقوه برای محاسبه هزینه قدرت تهدید. پس از محاسبه هزینه پرواز بین هر گره درختی

p_{v}

p_{r a n d}

، گره جدید بالقوه با حداقل هزینه پرواز به عنوان گره جدید انتخاب می شود

p_{n e w}

توسط

argmin ()

۳٫۴٫ به روز رسانی گره والد بر اساس هزینه پرواز

در بخش ۳٫۲ ، ما از اطلاعات اکتشافی شامل قدرت تهدید و هزینه طول مسیر برای هدایت گسترش گره جدید استفاده می کنیم، به طوری که FC-RRT* به محض تعیین گره جدید، طول مسیر و الزامات ایمنی برنامه ریزی مسیر پهپاد را برآورده می کند. به منظور هدایت بیشتر تولید مسیر، رویکرد ارزیابی استفاده از فاصله اقلیدسی به عنوان گره والد به روز رسانی در RRT* استاندارد نیز باید بهبود یابد. بنابراین، ما تابع هزینه پرواز را به به‌روزرسانی گره والد بهینه در FC-RRT* معرفی می‌کنیم تا یک مسیر بهینه را برنامه‌ریزی کنیم که بتواند به طور همزمان با قدرت تهدید و طول مسیر ارزیابی شود.

برای تعیین محدوده منطقه همسایه، گره های درختی از توپ با تنظیم شعاع انتخاب شدند

γ_{3} {(\log i / i)}^{1 / 3}

(جایی که

γ_{3} > 2^{n} (1 + 1 / n) μ [C_{f r e e}]

) [ ۴۲ ].

رویکرد به روز رسانی گره والد در همسایگی FC-RRT* در الگوریتم ۳ نشان داده شده است، و تحلیل زیر اولین فراخوانی را انجام می دهد. $rewire_ImpRRT * ()$ به عنوان مثال. RRT* استاندارد ابتدا تشخیص می دهد که آیا لبه $(p_{n e w}, p_{n e a r})$ بدون برخورد است و اگر درست باشد، گره والد بر اساس معیار اقلیدسی به روز می شود [ ۲۱ ]. با این حال، برای پهپاد، اندازه گیری مسیر به تنهایی نمی تواند ایمنی مسیر را تضمین کند. علاوه بر این، گره منطقه همسایه $p_{n e a r}$ با کمترین هزینه طول مسیر ممکن است محدودیت زاویه چرخش یا محدودیت زاویه صعود/سرخوردن را برآورده نکند. علاوه بر این، یک محدودیت حداکثر طول مسیر برای پهپاد وجود دارد. اگر طول مسیر برنامه ریزی شده از حد حداکثر برد بیشتر شود، پهپاد نمی تواند ماموریت را کامل کند.

الگوریتم ۳:

rewire_ImpRRT * (x_{1}, x_{2})

\begin{array}{l} 1 : if (collision_free (x_{1}, x_{2}) \land \\ UAV_free (x_{1}, x_{2})) then \\ 2 : c \leftarrow f_{c} (x_{1}, x_{2}) \\ 3 : if (f_{c, T} (x_{1}) + c < f_{c, T} (x_{2}) \land \\ lenth_\max (x_{1}, x_{2})) \leq L_{\max} then \\ 4 : T . parent (x_{2}) \leftarrow x_{1} \end{array}

بنابراین، لبه اتصال گره والد بالقوه و گره جدید شناسایی می شود تا مشخص شود که آیا محدودیت های عملکرد را برآورده می کند یا خیر (از طریق $UAV_free ()$ ، و اینکه آیا لبه در محیط پرواز بدون برخورد است (از طریق $collision_free ()$ ). سپس، به‌روزرسانی بهینه گره والد را با معرفی تابع هزینه پرواز ارزیابی کردیم تا تضمین کنیم که پهپاد از تهدید دور نگه داشته می‌شود و در عین حال کوتاه‌ترین مسیر را نیز به دست می‌آوریم. هزینه پرواز از نود شروع $p_{s t a r t}$ از طریق هر کدام $p_{n e a r}$ به $p_{n e w}$ جداگانه محاسبه می شود. علاوه بر این، پس از آن، $p_{n e a r}$ با کمترین هزینه به عنوان گره والد انتخاب می شود. سرانجام، $lenth_\max ()$ برای تعیین اینکه آیا محدودیت طول مسیر حداکثر برآورده شده است یا خیر استفاده می شود. را $lenth_\max ()$ به عنوان محاسبه می شود

lenth_max (x 1, x 2) = f l (p s t a r t, x 1) + f l (x 1, x 2) + | | p g o a l - x 2 | |

(۱۵)

۴٫ تجزیه و تحلیل

در این بخش، الگوریتم FC-RRT* به صورت تئوری در ترکیب با RRT* [ ۳۲ ] تحلیل می‌شود. از طریق تجزیه و تحلیل، ما ثابت می‌کنیم که FC-RRT* پیشنهادی دارای کامل بودن احتمالی و بهینه مجانبی است. در همین حال، پیچیدگی محاسباتی مجانبی اساساً با RRT* یکسان است.

۴٫۱٫ کامل بودن احتمالی

این بخش کامل بودن احتمالی FC-RRT* را تجزیه و تحلیل می کند. اکثر الگوریتم‌های برنامه‌ریزی مسیر مبتنی بر نمونه‌برداری از نظر احتمالی کامل هستند و تعریف کامل بودن احتمالی در زیر نشان داده شده است.

تعریف ۳ (کامل احتمالی ).

با توجه به گره شروع و مجموعه گره های هدف مورد نظر، اگر برای هر مشکل برنامه ریزی مسیر امکان پذیر قوی، معادله زیر برآورده شود، یعنی :

lim inf n \to \infty P (σ n, A L G \cap P g o a l \neq \emptyset) = ۱,

(۱۶)

الگوریتم $A L G$ احتمال کامل در نظر گرفته می شود .

با اشاره به شرح کامل بودن احتمال در تعریف ۳، کامل بودن احتمال FC-RRT* در قضیه ۱ توضیح داده شده است .

قضیه ۱ ( کامل احتمالی FC-RRT*).

هنگامی که تعداد نمونه های داده شده بی نهایت باشد، احتمال FC-RRT* برای یافتن راه حل عملی برای هر مسئله برنامه ریزی مسیر امکان پذیر قوی یک است، یعنی:

lim inf n \to \infty P (σ n, F C - R R T * \in C f r e e, σ n, F C - R R T * (0) = p s t a r t, σ n, F C - R R T * (1) \in P g o a l) = 1

(۱۷)

اثبات قضیه ۱ .

اثبات قضیه ۱ بر اساس سه استدلال زیر است:

درخت تصادفی تولید شده توسط FC-RRT* باید شامل باشد $p_{s t a r t}$ به عنوان یکی از رئوس آن در همین حال، گره هدف باید در مجموعه گره های هدف مورد نظر باشد $P_{g o a l}$ ، یعنی $σ_{n, F C - R R T *} (0) = p_{s t a r t}, σ_{n, F C - R R T *} (1) \in P_{g o a l}$ ، که همان RRT* است.
مشابه RRT *، درخت برنامه ریزی FC-RRT* متصل است (الگوریتم ۱ را ببینید). به عبارت دیگر، هر نمونه تصادفی را می توان به نزدیکترین راس در همسایه درخت متصل کرد.
FC-RRT* گره هدف را در مجموعه گره های هدف مورد نظر قرار می دهد. بنابراین، زمانی که نمونه‌گیری تصادفی بی‌نهایت باشد، احتمال ایجاد درخت تصادفی FC-RRT* به ناحیه هدف نزدیک به یک است. □

بر اساس سه استدلال بالا، ما می توانیم ثابت کنیم که وقتی هر مشکل برنامه ریزی مسیر داده می شود، FC-RRT* می تواند یک مسیر امکان پذیر پیدا کند و با نزدیک شدن تعداد نمونه ها به بی نهایت، به احتمال ۱ نزدیک شود (فرض این نتیجه گیری این است که که یک راه حل عملی برای یک مشکل برنامه ریزی مسیر مشخص وجود دارد). بنابراین، FC-RRT* و RRT* نیز کامل بودن احتمال را تضمین می کنند.

۴٫۲٫ بهینه مجانبی

FC-RRT* بهینه مجانبی استاندارد RRT * را به ارث می برد. این بخش بهینه‌سازی مجانبی FC-RRT* را در برخورد با مسائل برنامه‌ریزی مسیر تحلیل می‌کند. در ابتدا، تعریف بهینه مجانبی به صورت زیر ارائه می شود.

تعریف ۴ ( بهینه مجانبی ).

برای هر مشکل برنامه ریزی مسیر، زمانی که تعداد نمونه ها به بی نهایت نزدیک شود، الگوریتم

A L G

اگر بتواند نمودار درختی راه حل کم هزینه را برگرداند، از نظر مجانبی بهینه است. مشابه RRT*، فرضیات زیر را برای اثبات اینکه FC-RRT* از نظر مجانبی بهینه است، تنظیم کردیم. آنها برای اثبات اینکه RRT * از نظر مجانبی بهینه است استفاده شده است [ ۳۲ ].

فرض ۱ ( افزایش هزینه) .

برای هر دو مسیر بدون برخورد، به عنوان مثال،

σ_{1}, σ_{2} \in C_{f r e e}

، تابع هزینه

f_{c} (\cdot)

باید راضی کند

f_{c} (σ_{1}) \leq f_{c} (σ_{1} | σ_{2}) : f_{c} (σ_{1}) + f_{c} (σ_{2})

فرض ۲ ( تداوم هزینه ).

تابع هزینه

f_{c} (\cdot)

یک تابع پیوسته Lipschitz است و یک ثابت وجود دارد

δ

به طوری که هر دو مسیر بدون برخورد بسیار نزدیک

σ_{1} : [0, g_{1}], σ_{2} : [0, g_{2}] \in C_{f r e e}

، داشتن

| f_{c} (σ_{1}) - f_{c} (σ_{2}) | \leq δ \sup_{τ : [0, 1]} ‖ σ_{1} (τ g_{1}) - σ_{2} (τ g_{2}) ‖

فرض ۳ (

γ

-فاصله بین مانع). برای هر گره نمونه برداری

p

، یک ناحیه توپ در فضای بدون برخورد C با شعاع وجود دارد

γ \in ℝ_{> 0}

و مرکز یک گره دیگر

p_{1} \in C_{f r e e}

، یعنی

p \in B_{P_{1}, γ}

بر اساس مفروضات فوق، توصیف بهینه مجانبی FC-RRT* به شرح زیر ارائه می شود:

قضیه ۲ ( بهینه مجانبی FC-RRT*).

فرضیات ۱، ۲ و ۳ را بگذارید. وقتی تعداد نمونه ها نامحدود است، احتمال همگرا شدن تدریجی FC-RRT* به حل بهینه مسئله برنامه ریزی مسیر داده شده است.

P (lim sup n \to \infty (c (σ n, F C - R R T *) = c *)) = ۱,

(۱۸)

جایی که $c^{*}$ راه حل بهینه مسئله برنامه ریزی مسیر است .

اثبات قضیه ۲ .

فرض ۱ نشان می دهد که تابع هزینه الگوریتم باید افزایشی باشد و هزینه نمی تواند منفی باشد. هنگامی که الگوریتم فرآیندهای سیم کشی مجدد را اجرا می کند، بخش های مسیر متفاوتی برای مقایسه باید اضافه شوند (نگاه کنید به $rewire_ImpRRT * ()$ ). استاندارد RRT * فاصله اقلیدسی را به عنوان هزینه در نظر می گیرد که باید فرض ۱ را برآورده کند (یعنی $f_{c} (σ_{1}) = f_{l} (σ_{1})$ ). تابع هزینه $f_{c} (\cdot)$ FC-RRT* شامل هزینه طول مسیر است $f_{l} (\cdot)$ و هزینه تهدید مسیر $f_{t} (\cdot)$ ، و $f_{t} (\cdot) \geq 0$ . برای هر ترکیب وزنی $[λ_{1}, λ_{2}]$ ( $λ_{1} + λ_{2} = 1$ )

f c (σ ۱) : f l (σ ۱) + f t (σ ۱) \leq f l (σ ۱) + f t (σ ۱) + f l (σ ۲) + f t (σ ۲)

(۱۹)

بنابراین، FC-RRT* نیز فرض ۱ را برآورده می کند. □

فرض ۲ نشان می دهد که دو مسیر بسیار نزدیک هزینه های مشابهی دارند. مشابه RRT*، FC-RRT* نیز برای این فرض صادق است. برای دو مسیر بسیار نزدیک، طول مسیر مشابه است. علاوه بر این، از آنجا که فاصله بین دو مسیر نزدیک و تهدید بسیار مشابه است، هزینه تهدید مسیر نیز مشابه است.

فرض ۳ نشان می دهد که یک منطقه بدون برخورد در اطراف مسیر امکان پذیر وجود دارد. الگوریتم می تواند گره نمونه برداری با کمترین هزینه را از گره های نمونه گیری در منطقه انتخاب کند تا الگوریتم را به مسیر بهینه همگرا کند. تعیین شعاع محله

γ

با استفاده از الگوریتم FC-RRT* مانند RRT* است، به عنوان مثال،

γ_{3} \geq γ_{3}^{*}

. این تضمین می کند که حداقل یک گره از درخت

τ = (υ, ε)

هنگامی که تعداد زیادی نمونه گرفته می شود در این منطقه قرار می گیرد. این بدان معنی است که هنگام تماس با

rewire_ImpRRT * ()

برای انتخاب گره والد، گره با هزینه کمتر احتمالاً برای بهینه سازی مسیر دوباره سیم کشی می شود. بنابراین، زمانی که زمان‌های نمونه‌برداری به بی‌نهایت نزدیک می‌شوند، احتمال تغییر هزینه مسیر وجود دارد

‖ f_{c} (σ_{1}) - f_{c} (σ_{1}) ‖

از دو مسیر امکان پذیر تقریباً صفر است. بنابراین، ثابت شده است که FC-RRT* از نظر مجانبی بهینه است.

۴٫۳٫ پیچیدگی محاسباتی

در این بخش، ما عمدتاً پیچیدگی محاسباتی مجانبی استاندارد RRT* و FC-RRT* را مقایسه می‌کنیم. تحلیل مقایسه ای نشان می دهد که پیچیدگی محاسباتی مجانبی دو الگوریتم تقریباً یکسان است.

به منظور مقایسه پیچیدگی محاسباتی پیشرونده RRT* و FC-RRT*، باید زمان مورد نیاز را با مقایسه تعداد مراحل اجرای هر فرآیند ارزیابی کنیم. توجه داشته باشید که

Sample (\cdot)

collision_free (\cdot)

Near (\cdot)

فرآیندهای دو الگوریتم یکسان است و می توان آنها را در تعداد معینی از مراحل انجام داد (یعنی اجرای این رویه ها مستقل از تعداد رئوس درخت است.). برای هر تکرار

i

Sample (\cdot)

حداقل یک بار اجرا می کند،

collision_free (\cdot)

حداقل سه بار اجرا می شود و

Near (\cdot)

حداقل یک بار اجرا می شود. تفاوت این است که RRT* استاندارد گسترش گره جدید را به دو فرآیند تقسیم می‌کند (به عنوان مثال، نویسندگان [ ۳۲ ] آنها را

Nearest (\cdot)

steer (\cdot)

فرآیندها)، و الگوریتم FC-RRT* پیشنهادی مستقیماً از طریق گره جدید به گره باز می گردد

Heuristic_\cos t (\cdot)

روند. بنابراین، پیچیدگی محاسباتی مجانبی از

Heuristic_\cos t (\cdot)

فرآیند باید در نظر گرفته شود

را

steer (\cdot)

فرآیند RRT* تنها یک بسط ساده گره ها است و اساساً بر زمان محاسبه تأثیر نمی گذارد. با این حال، هر دو

Heuristic_\cos t (\cdot)

Nearest (\cdot)

فرآیندها شامل مشکل یافتن نزدیکترین همسایه است. مطالعه انجام شده در [ ۴۳ ] نشان می‌دهد که جستجوی نزدیک‌ترین همسایه حداقل زمان لگاریتمی طول می‌کشد و هر تکرار با توجه به تغییراتی که در نقاط نمونه‌گیری رخ می‌دهد تغییر می‌کند (یعنی اجرای فرآیند به تعداد رئوس درخت مربوط می‌شود). . برای FC-RRT* و RRT*، چون هر تکرار فقط یک نمونه دارد، گره های آنها در تکرار

i

یکسان هستند، یعنی

V_{i}^{R R T *} = V_{i}^{F C - R R T *}

. بنابراین، هم RRT* و هم FC-RRT* حداقل به زمان لگاریتمی نیاز دارند

\log (n)

برای یافتن نزدیکترین همسایه در تکرار

i

. بنابراین، FC-RRT* و RRT* تقریباً پیچیدگی محاسباتی مجانبی یکسانی دارند.

قضیه ۳٫

یک A ثابت وجود دارد که،

lim n \to \infty E [S R R T * i S F C - R R T * i] \leq α,

(۲۰)

جایی که $S_{i}^{R R T *}$ و $S_{i}^{F C - R R T *}$ تعداد مراحل درگیر در RRT* و FC-RRT* را به ترتیب در تکرار نشان می دهد.

۵٫ شبیه سازی و تجزیه و تحلیل

به منظور ارزیابی جامع اثربخشی الگوریتم FC-RRT* پیشنهادی، ارزیابی و تحلیل شبیه سازی را انجام دادیم.

هیچ مدل استاندارد زیست محیطی پذیرفته شده ای در برنامه ریزی مسیر پهپاد وجود ندارد. برای روش‌های برنامه‌ریزی مسیر مبتنی بر نمونه‌برداری، ما معمولاً پیکربندی‌های اولیه را برای نمایش موانع یا تهدیدات در صحنه اتخاذ می‌کنیم. بنابراین، در این مقاله، هنگام ایجاد مدل تهدید، مانند [ ۴۴]، یک مدل نیمکره ای برای توصیف تقریباً رادار هشدار دهنده و منطقه تهدید آن پیاده سازی شده است و مدل از مدل استوانه ای برای توصیف تقریباً ساختمان ضد هوایی و برد حمله آن استفاده می کند. مدل مخروطی برای توصیف تقریباً برج مورد استفاده قرار گرفت (از آنجایی که برج هیچ قابلیت تشخیص یا ضربه ای ندارد، به عنوان منطقه پرواز ممنوع در نظر گرفته می شود). با این حال، استفاده از یک پیکربندی اولیه منجر به اطلاعات زیادی در مورد زمین از دست رفته می شود. بنابراین، در این مقاله، یک نقشه ارتفاع واقعی برای نشان دادن زمین به منظور انعکاس واقعی اطلاعات تهدید زمین ساخته شد.

جدول ۱ برخی از پارامترهای اساسی FC-RRT* را نشان می‌دهد که در آن موارد ۱، مورد ۲ و مورد ۳ به ترتیب وزن‌های مختلف در تابع هزینه پرواز هستند. علاوه بر این، پارامترهای تعیین شده برای رادار، اسلحه ضد هوایی و برج نشان داده شده است.

۵٫۱٫ شبیه سازی و تحلیل FC-RRT* در محیط پیچیده

از طریق محیط پرواز پیچیده، FC-RRT* شبیه سازی و تجزیه و تحلیل می شود تا اثربخشی و برتری اطلاعات اکتشافی را تأیید کند تا گسترش گره جدید و به روز رسانی گره والد را هدایت کند.

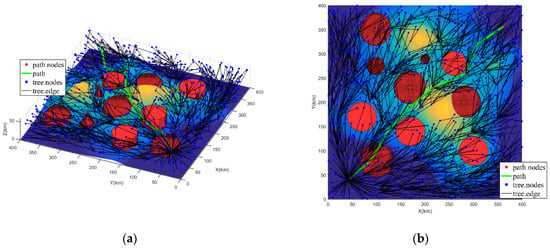
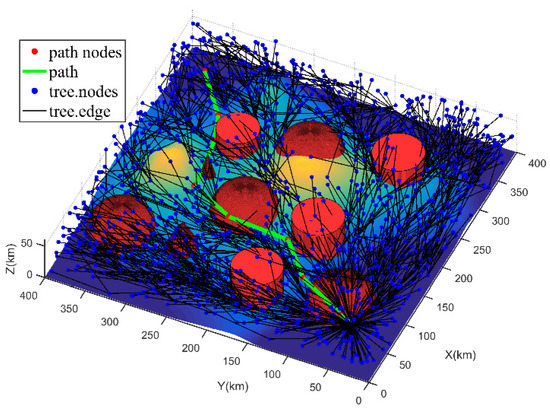
شکل ۳ ، شکل ۴ و شکل ۵ نمودار درختی هدایت شده و مسیر برنامه ریزی FC-RRT* را در سه حالت مختلف نشان می دهد. جدول ۲ نتایج آماری شامل تعداد گره های درختی، تعداد گره های درختی در محدوده تهدید را نشان می دهد.

L_{t h}

، طول مسیر، حداقل فاصله بین مسیر و تهدیدات، مقدار تهدید مسیر، نسبت طول مسیر تاثیر تهدید در طول کل مسیر، و میزان موفقیت ۵۰ آزمایش.

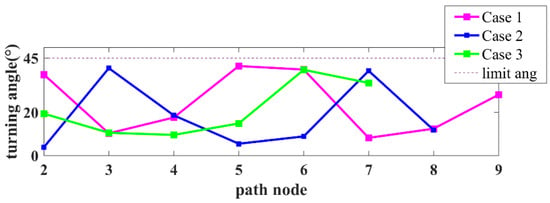
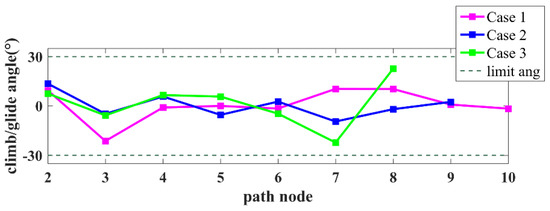
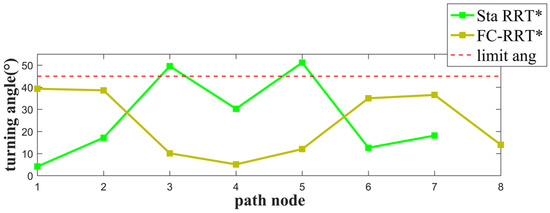
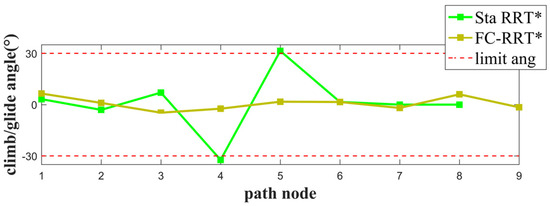
از میزان موفقیت شبیه سازی در جدول ۲ ، پس از بهبود تعیین گره جدید و به روز رسانی گره والد، و معرفی محدودیت پهپاد، FC-RRT* همچنان برنامه ریزی مسیر موفق را در محیط پیچیده مدیریت کرد. از شکل ۶ و شکل ۷ ، مسیر برنامه ریزی شده با استفاده از FC-RRT*، زاویه چرخش و محدودیت های زاویه صعود/سرخوردن را برآورده می کند، و زوایای چرخش و صعود/سرخوردن نسبتاً هموار هستند.

علاوه بر این، از آنجایی که تابع هزینه پرواز به عنوان اطلاعات اکتشافی برای هدایت گسترش گره جدید اعمال می شود، از شکل ۳ ، شکل ۴ و شکل ۵ ، توزیع گره های درختی به طور قابل توجهی بر اساس سه وزن متفاوت است. مورد ۱ نشان دهنده یک تخصیص وزن است که بر ایمنی مسیر با در نظر گرفتن کمی هزینه طول مسیر تمرکز دارد. از این رو، گره های درختی در شکل ۳ در نزدیکی تهدیدات گسترش نمی یابند. اکثر آنها عمدتاً در فاصله معینی از تهدید متمرکز هستند. علاوه بر این، از جدول ۲ ، تعداد گره ها در محدوده تهدید

L_{t h}

برای مورد ۱ نشان می دهد که تنها چند گره درختی در محدوده تهدید قرار دارند. مورد ۲ تخصیص وزن را برای الزامات ایمنی مسیر و طول مسیر نشان می دهد، بنابراین تعداد معینی از گره های درختی در محدوده ضربه تهدید وجود دارد که در شکل ۴ نشان داده شده است . در همین حال، همانطور که در جدول ۲ نشان داده شده است ، تعداد گره های درختی در محدوده تهدید

L_{t h}

مورد ۲ در مقایسه با مورد ۱ افزایش یافته است. تخصیص وزن مورد ۳ نشان دهنده تمایل به دستیابی به کمترین کاهش مسیر است، حتی اگر ایمنی مسیر را قربانی کند. بنابراین، از شکل ۵ ، گره های درخت اساساً به طور مساوی در محیط نمونه گیری توزیع شده اند. علاوه بر این، تعداد گره ها در محدوده تهدید

L_{t h}

در جدول ۲ نیز بالاترین میزان است. از موارد فوق، اوزان

λ_{l}

λ_{t}

در تابع هزینه پرواز بر گسترش گره های جدید تأثیر می گذارد. یعنی، استفاده از تابع هزینه پرواز به عنوان اطلاعات اکتشافی می تواند به طور موثر گسترش گره های جدید را هدایت کند، بنابراین برنامه ریزی مسیر را از جلویی هدایت می کند.

در ترکیب با شکل ۳ ، شکل ۴ و شکل ۵ و جدول ۲ ، مسیرهای برنامه ریزی تحت سه توزیع وزن متفاوت کاملاً متفاوت است. از شکل ۳ ، مسیر برنامه ریزی در مورد ۱ فاصله بیشتری بین مسیر و تهدید دارد، که همچنین باعث طول مسیر طولانی تر می شود. ضمناً مقایسه نتایج آماری سه مورد در جدول ۲مشاهده می شود که Case1 بیشترین فاصله بین مسیر و تهدید را دارد. مقدار قدرت تهدید و درصد مسیرهای تهدید کمترین است. و طول مسیر طولانی ترین است. این تأیید می کند که در وزن Case1، مسیر برنامه ریزی بر ایمنی مسیر متمرکز است، اگرچه هزینه طول مسیر گران تر است. از شکل ۴ برای مورد ۲، فاصله بین مسیر برنامه ریزی شده و تهدید و هزینه طول مسیر هر دو در سطح متوسط هستند (مقایسه با موارد دیگر). علاوه بر این، از جدول ۲ ، نتایج آماری مورد ۲ در سه مورد متوسط است. این ثابت می کند که ایمنی مسیر اهمیت مشابهی با طول مسیر در وزن مورد ۲ دارد. همانطور که در شکل ۵ مشاهده می شود.برای مورد ۳، طول مسیر کوتاه ترین است، اما فاصله بین مسیر و تهدید کوتاه ترین است. این همچنین در مقایسه نتایج آماری در جدول ۲ منعکس شده است که در آن طول مسیر کوتاهترین وزن از سه وزن است. با این حال، فاصله بین مسیر و تهدیدها کمترین است و مقدار مسیر تهدید و درصد مسیر تهدید بزرگترین هستند. از این رو، اگرچه وزن مورد ۳ کوتاه ترین مسیر را برنامه ریزی می کند، اما به شدت بر ایمنی مسیر تأثیر می گذارد و احتمال بقا را کاهش می دهد. با توجه به موارد فوق، تابع هزینه پرواز می تواند به طور موثر برنامه ریزی مسیر پهپاد را هدایت کند و مسیر بهینه مورد نیاز کاربر را به دست آورد.

به طور خلاصه، نتایج شبیه‌سازی نشان می‌دهد که FC-RRT* برای برنامه‌ریزی مسیر پهپاد در محیط پیچیده مناسب است و الزامات ایمنی مسیر و طول مسیر را برآورده می‌کند. از نظر گسترش گره جدید جلویی و به‌روزرسانی گره والد پشتیبان، تابع هزینه پرواز و محدودیت پرواز دو بار معرفی شده‌اند، به این معنی که FC-RRT* مسیری بهینه را با کوتاه‌ترین طول برنامه‌ریزی می‌کند و در عین حال الزامات ایمنی مسیر را برآورده می‌کند. علاوه بر این، تخصیص وزن توابع مختلف هزینه پرواز در الگوریتم می‌تواند تولید مسیرهایی با نیازهای مختلف را هدایت کند. مورد ۱ نشان می دهد که مسیر با بیشترین احتمال بقا ترجیح داده می شود، در حالی که اساساً هیچ نیازی برای هزینه طول مسیر وجود ندارد. از این رو، می توان از آن برای ماموریت های نظامی مانند کروز و نظارت دوربرد در میدان جنگ استفاده کرد. مورد ۲ نشان می دهد که هم ایمنی مسیر و هم طول مسیر اهمیت بیشتری دارند. می توان از آن برای ماموریت های نظامی برای کاربردهایی مانند سرکوب دشمن و برای ضربه زدن به تاسیسات دشمن استفاده کرد. کاربرد Case 3 به پهپاد اجازه می دهد تا به سرعت از تهدیدات دشمن عبور کند و در عین حال احتمال بقا و توانایی اجتناب از تهدیدات را نادیده بگیرد، بنابراین می توان از آن برای فرار سریع و موقعیت های دفاعی غافلگیرکننده استفاده کرد.

۵٫۲٫ مقایسه و بحث

به منظور بررسی بیشتر برتری FC-RRT*، آن را با RRT* استاندارد مقایسه کردیم. در این آزمایش، محیط پرواز به گونه ای تنظیم شده است که مقایسه الگوریتم ها را به وضوح نشان دهد. پارامترهای تنظیم شده در جدول ۳ و سایر پارامترها در جدول ۱ نشان داده شده است.

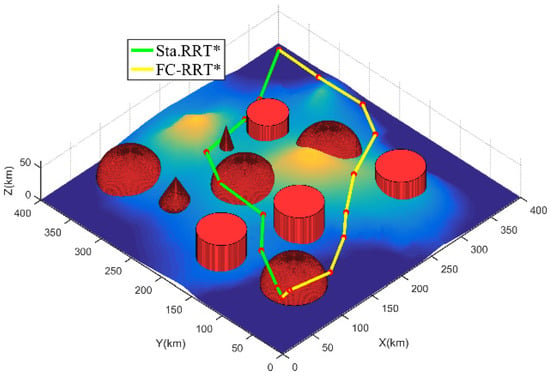
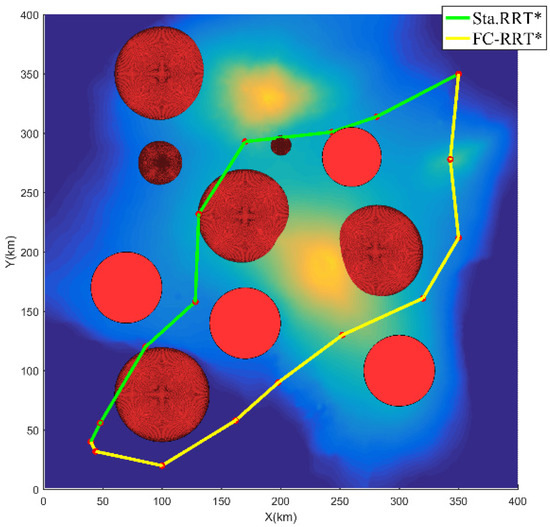
از توزیع گره درختی در شکل ۸ ، از آنجایی که RRT* فقط فاصله اقلیدسی را زمانی در نظر می گیرد که گره های جدید گسترش می یابند، گره های درختی تولید شده توسط الگوریتم به طور مساوی در فضای نمونه گیری توزیع می شوند. با این حال، الگوریتم FC-RRT* تابع هزینه پرواز پیشنهادی را برای الهام بخشیدن به گسترش گره جدید هدایت می کند، بنابراین تعداد گره های درختی در نزدیکی منطقه تهدید به طور قابل توجهی کوچکتر است (به شکل ۳ مراجعه کنید ). علاوه بر این، این با مقایسه تعداد گره های درختی در محدوده تهدید نشان داده می شود

L_{t h}

در جدول ۴ . در همین حال، از جدول ۴، طول مسیر برنامه ریزی RRT* در مقایسه با FC-RRT* کوتاهتر است. با این حال، در مقایسه با FC-RRT*، مسیر برنامه‌ریزی شده توسط RRT* دارای ارزش تهدید بزرگ‌تر و نزدیک‌ترین فاصله به تهدید است و بیشتر مسیر در محدوده تهدید قرار دارد. با این حال، با توجه به ایمنی مسیر پهپاد در محیط پیچیده ایجاد شده برای این شبیه‌سازی‌ها، مسیر برنامه‌ریزی‌شده توسط FC-RRT* تابع هزینه پرواز را برای هدایت گسترش گره‌های جدید و به‌روزرسانی مستقیم گره والد اتخاذ می‌کند. اگرچه این رویکرد منجر به یک مسیر طولانی‌تر می‌شود، اما هم مقدار تهدید مسیر و هم درصد مسیر تحت‌تاثیر تهدیدها کوچک‌تر از RRT* است و نزدیک‌ترین فاصله تا تهدید نسبتاً زیاد است. بنابراین، مسیر RRT* بسیار نزدیک به تهدید است که بر ایمنی مسیر تأثیر می گذارد. در مقابل، در FC-RRT*، مسیر برنامه ریزی دور از تهدید است.

علاوه بر این، از شکل ۹ و شکل ۱۰ ، مسیر برنامه ریزی شده توسط RRT* کوتاه تر است اما دارای پیچ های با زاویه بزرگ تر است، در حالی که FC-RRT* مسیری با پیچ های کمتر ایجاد می کند و مسیر هموارتر است. علاوه بر این، از شکل ۱۱ و شکل ۱۲ ، برخی از زوایای چرخش و صعود/سرخوردن نقاط مسیر محدودیت پهپاد را در RRT* استاندارد برآورده نمی‌کنند. با این حال، برای FC-RRT*، مسیر برنامه ریزی شده محدودیت های زاویه را برآورده می کند و نسبتا هموار است.

به طور خلاصه، با مقایسه عملکرد RRT* و FC-RRT* برای برنامه ریزی مسیر پهپاد در محیط پیچیده، مسیر برنامه ریزی شده توسط RRT* به تهدید نزدیک است، به این معنی که ایمنی مسیر تضمین نمی شود. علاوه بر این، چرخش‌های زاویه‌ای بسیار زیاد وجود دارد و نمی‌تواند محدودیت‌های پرواز را برآورده کند. از این رو، RRT* برای برنامه ریزی مسیر پهپاد مناسب نیست. با این حال، برای FC-RRT*، هم قدرت تهدید مسیر و هم هزینه طول مسیر در نظر گرفته می‌شود و تابع هزینه پرواز برای هدایت گره جدید به سمت گسترش طراحی شده است تا گره جدید بتواند به محیطی گسترش یابد که الزامات ایمنی مسیر را برآورده می‌کند. . با این حال، برای FC-RRT*، گره جدید به دلیل استفاده از تابع هزینه پرواز که شامل قدرت تهدید و هزینه طول مسیر است، به محیط ایمنی مسیر گسترش می‌یابد. علاوه بر این، تابع هزینه پرواز برای راهنمایی بهینه سازی گره والد استفاده می شود. بنابراین، مسیر برنامه ریزی شده توسط FC-RRT* نسبتاً دور از تهدیدات است و ایمنی مسیر را تضمین می کند. در عین حال، با توجه به معرفی محدودیت های پرواز در FC-RRT*، مسیر محدودیت ها را برآورده می کند و مسیر در مقایسه با RRT* استاندارد هموارتر است. این آزمایش ثابت می کند که FC-RRT* برای برنامه ریزی مسیر پهپاد در یک محیط پیچیده مناسب است و می تواند الزامات عملیات نظامی را برآورده کند.

۵٫۳٫ بحث قبل از آماده سازی آزمایش پرواز واقعی

مقاله ما عمدتاً یک روش برنامه ریزی مسیر سه بعدی را مورد مطالعه قرار می دهد که برای پهپادها مناسب است. با توجه به پیچیدگی محیط میدان نبرد و تنوع تهدیدات موانع، ما یک الگوریتم FC-RRT* را برای برآوردن الزامات برنامه ریزی پهپاد در این محیط پیشنهاد کردیم. برای ایجاد الگوریتم، مقادیر کاربرد عملی خاصی را مورد مطالعه قرار دادیم و بحث کاربرد عملی الگوریتم را در این بخش گسترش دادیم.

پهپادهای چهار روتوری را که در آزمایشگاه برای اندازه‌گیری و ثبت پارامترهای مربوطه طراحی کرده‌ایم انتخاب کردیم و داده‌های به‌دست‌آمده را با نتایج شبیه‌سازی الگوریتم در این مقاله مقایسه کردیم تا ببینیم آیا نتایج شبیه‌سازی در این مقاله می‌تواند مطابق با پارامتر باشد. محدودیت های پهپاد در آزمایشات پروازی آینده در شرایط واقعی، همان پهپاد را انتخاب خواهیم کرد. پهپاد چهار روتور در شکل ۱۳ و پارامترهای پهپاد مربوطه در جدول ۵ نشان داده شده است. به منظور معرفی کامل پلت فرم چهار روتوری که در آینده از آن برای انجام آزمایشات پروازی استفاده خواهیم کرد، پارامترهای مربوط به خلبان خودکار خود طراحی شده در جدول A1 در پیوست A معرفی شده است.

از جدول A1 می توان دریافت که وقتی یک باتری با ظرفیت بار ۵۰۰۰ میلی آمپر ساعت پرواز می کند، حداکثر زمان پرواز پهپاد ۲۸ دقیقه و حداکثر سرعت پرواز پهپاد ۴ متر بر ثانیه است. همراه با حداکثر طول مسیر برنامه ریزی شده پهپاد ارائه شده در جدول ۲ و جدول ۴ در بخش ۵در این مقاله مشاهده می شود که نتایج شبیه سازی می تواند شرایط پارامتر طول پرواز واقعی پهپاد را برآورده کند و می تواند پرواز را با یک بار توان کامل کامل کند. در عین حال، حداکثر محدودیت زاویه فرمان و حداکثر محدودیت زاویه صعود پهپاد تنظیم شده در شبیه سازی، محدودیت زاویه پهپاد چهار روتور را برآورده می کند. بنابراین، می‌توانیم به طور مقدماتی تعیین کنیم که الگوریتم توسعه‌یافته در این مقاله می‌تواند آزمایش‌های پرواز را با استفاده از پلت فرم پهپاد چهار روتور تکمیل کند. البته این فقط یک قضاوت اولیه قبل از آزمایش واقعی پرواز است. برای برخی از پارامترهای واقعی، مانند تأثیر آب و هوای خاص و جهت باد، می توان داده های دقیقی را در طول پروازهای آزمایشی واقعی در آینده به دست آورد.

۶٫ نتیجه گیری

در این مقاله، ما یک الگوریتم برنامه‌ریزی مسیر برای پهپادها در محیط‌های پیچیده به نام FC-RRT* پیشنهاد می‌کنیم که به طور جامع طول مسیر و ایمنی مسیر را در نظر می‌گیرد تا تضمین کند که یک پهپاد قادر به انجام ماموریت‌های نظامی ایمن است. FC-RRT* استاندارد RRT* را بهبود و بهینه می کند. ابتدا، ما یک تابع هزینه پرواز طراحی کردیم که هم قدرت تهدید مسیر و هم هزینه طول مسیر را شامل می شود. سپس، رویکردی با استفاده از تابع هزینه پرواز به عنوان اطلاعات اکتشافی برای هدایت گسترش گره‌های جدید در قسمت جلویی پیشنهاد می‌شود، که گره‌های جدید را قادر می‌سازد تا به فضای نمونه‌گیری با ایمنی مسیر بالا گسترش یابند. پس از آن، هم تابع هزینه پرواز و هم محدودیت‌های پرواز را در به‌روزرسانی گره والد در بک‌اند در نظر گرفتیم. مسیر برنامه ریزی شده توسط FC-RRT* دارای کمترین مسافت و بالاترین ایمنی است زیرا هم قسمت جلویی و هم انتهایی را هدایت می کند. سپس، FC-RRT* را عمیقاً تحلیل کردیم. شبیه سازی ها و مقایسه ها ثابت می کند که FC-RRT* برای برنامه ریزی مسیر پهپاد در یک محیط پیچیده مناسب است. علاوه بر این، FC-RRT* را می توان برای ماموریت های نظامی مختلف، مانند کروز یا نظارت دوربرد، ضربه زدن به تأسیسات دشمن، فرار سریع از میدان جنگ یا دفاع غافلگیرکننده به کار برد.

البته این الگوریتم تنها راه مقابله با برنامه ریزی مسیر پهپاد در محیط های پیچیده نیست. الگوریتم‌های هوشمند مانند الگوریتم ژنتیک نیز قادر به انجام این کار هستند، اما الگوریتم‌های هوشمند معمولاً پیچیدگی زیادی دارند. بنابراین، به عنوان یک الگوریتم با پیچیدگی محاسباتی نسبتاً کم، الگوریتم پیشنهادی در این مقاله با فرض به دست آوردن نتایج مشابه، کارایی محاسباتی را بهبود می بخشد. در همین حال، ما امیدواریم که در تحقیقات آینده تحقیقات عمیق تری در مورد این الگوریتم انجام دهیم، از جمله، اما نه محدود به بهبود نظری و تأیید پرواز واقعی الگوریتم، تا الگوریتم ما بتواند ارزش کاربردی قوی تری داشته باشد. علاوه بر این، FC-RRT* فقط برای برنامه ریزی مسیر UAV ایستا مناسب است، به این معنی که تمام اطلاعات محیطی باید شناخته شوند.

منابع

پاپادوپولو، ای.-ای. واسیلاکوس، سی. زوروس، ن. Soulakellis، برنامه‌ریزی پرواز پهپاد مبتنی بر DEM-N. برای نقشه‌برداری سه‌بعدی ژئوسایت‌ها: مورد پنجره تکتونیکی المپوس، لسبوس، یونان. ISPRS Int. J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۵۳۵٫ [ Google Scholar ] [ CrossRef ]
Patle، BK; بابو، ال جی; پاندی، ا. پرهی، DRK; Jagadeesh, A. A. A. A. A. A. در مورد استراتژی های برنامه ریزی مسیر برای ناوبری ربات متحرک. تعریف کنید. تکنولوژی ۲۰۱۹ ، ۱۵ ، ۵۸۲-۶۰۶٫ [ Google Scholar ] [ CrossRef ]
فو، بی. چن، ال. ژو، ی. ژنگ، دی. وی، ز. دای، جی. Pan, H. یک الگوریتم A* بهبود یافته برای برنامه ریزی مسیر ربات صنعتی با میزان موفقیت بالا و طول کوتاه. ربات. Auton. سیستم ۲۰۱۸ ، ۱۰۶ ، ۲۶-۳۷٫ [ Google Scholar ] [ CrossRef ]
ژائو، ال. یان، ال. هو، ایکس. یوان، جی. لیو، زی. کاوش خودکار و برنامه‌ریزی مسیر با کیفیت و کارآمد مسیر پهپاد در یک محیط ناشناخته. ISPRS Int. J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۶۳۱٫ [ Google Scholar ] [ CrossRef ]
Phung، MD; Ha، QP برنامه ریزی مسیر پهپاد پیشرفته با ایمنی با بهینه سازی ازدحام ذرات کروی مبتنی بر برداری. Appl. محاسبات نرم. ۲۰۲۱ ، ۱۰۷ ، ۱۰۷۳۷۶٫ [ Google Scholar ] [ CrossRef ]
لیائو، اس ال. زو، RM; وو، NQ; شیخ، TA; شرف، م. مصطفی، برنامه ریزی مسیر AM برای ردیابی هدف متحرک توسط پهپاد بال ثابت. تعریف کنید. تکنولوژی ۲۰۲۰ ، ۱۶ ، ۸۱۱-۸۲۴٫ [ Google Scholar ] [ CrossRef ]
وو، جی. آتیلا، من. تحسین، ت. ترزیف، م. Wang, LC روش برنامه ریزی مسیر سفر طولانی بر اساس نمودار دید چند مقیاسی برای کشتی های خودمختار. مهندس اقیانوس ۲۰۲۱ , ۲۱۹ , ۱۰۸۲۴۲٫ [ Google Scholar ] [ CrossRef ]
چی، دبلیو. دینگ، ز. وانگ، جی. چن، جی. Sun، L. یک روش برنامه ریزی مسیر ابتکاری کارآمد مبتنی بر نمودار ورونوی تعمیم یافته برای RRT ها در ربات های متحرک. IEEE Trans. الکترون صنعتی ۲۰۲۱ ، ۶۵ ، ۴۹۲۶-۴۹۳۷٫ [ Google Scholar ] [ CrossRef ]
فینک، دبلیو. بیکر، VR؛ بروکس، AJW; فلامیا، م. Dohm, JM; Tarbell، MA برنامه ریزی بهینه تراورس مریخ نورد در سطح جهانی به صورت سه بعدی با استفاده از الگوریتم Dijkstra برای سناریوهای استقرار چند هدفه. سیاره. علوم فضایی ۲۰۱۹ ، ۱۷۹ ، ۱۰۴۷۰۷٫ [ Google Scholar ] [ CrossRef ]
چن، ایکس. ژائو، ام. یین، ال. برنامه ریزی مسیر پویا پهپاد با اجتناب از موانع استاتیک و متحرک. جی. اینتل. ربات. سیستم تئوری کاربردی ۲۰۲۰ ، ۹۹ ، ۹۰۹-۹۳۱٫ [ Google Scholar ] [ CrossRef ]
ماجومدر، اس. الگوریتم پراساد، MS سه بعدی D∗ برای برنامه ریزی مسیر افزایشی در محیط غیرهمکاری. در مجموعه مقالات سومین کنفرانس بین المللی پردازش سیگنال و شبکه های یکپارچه، SPIN، نویدا، هند، ۱۱–۱۲ فوریه ۲۰۱۶٫ دوره ۱۳۹۵، ص ۴۳۱–۴۳۵٫ [ Google Scholar ]
بله، بی. تانگ، کیو. یائو، جی. Gao, W. برنامه ریزی مسیر بدون برخورد و بهینه سازی توالی تحویل در پرتودرمانی غیرهمسطح. IEEE Trans. سایبرن. ۲۰۱۹ ، ۴۹ ، ۴۲-۵۵٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
یوان، سی. لیو، جی. ژانگ، دبلیو. Pan, X. یک روش کش RRT کارآمد در محیط های پویا برای برنامه ریزی مسیر. غارت. Auton. سیستم ۲۰۲۰ , ۱۳۱ , ۱۰۳۵۹۵٫ [ Google Scholar ] [ CrossRef ]
وو، ی. وو، اس. Hu, X. برنامه‌ریزی مسیر مشارکتی پهپادهای UGV برای یک وظیفه نظارتی پایدار در محیط‌های شهری. IEEE Internet Things J. ۲۰۲۱ , ۸ , ۴۹۰۶–۴۹۱۹٫ [ Google Scholar ] [ CrossRef ]
یانگ، اچ. چی، جی. میائو، ی. سان، اچ. Li, J. الگوریتم ناوبری ربات جدید بر اساس الگوریتم مورچه دو لایه و بهینه سازی مسیر. IEEE Trans. الکترون صنعتی ۲۰۱۹ ، ۶۶ ، ۸۵۵۷–۸۵۶۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
راسخی پور، ی. خواجه پور، ع. چن، SK; لیتکوهی، ب. یک مدل بالقوه میدان محور برنامه ریزی مسیر پیش بینی کنترل کننده برای وسایل نقلیه جاده ای خودمختار. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۷ ، ۱۸ ، ۱۲۵۵-۱۲۶۷٫ [ Google Scholar ] [ CrossRef ]
لیو، ایکس. ژانگ، دی. ژانگ، تی. ژانگ، جی. Wang, J. یک روش جدید طرح مسیر مبتنی بر الگوریتم ترکیبی یادگیری تقویتی و بهینه‌سازی ازدحام ذرات. مهندس محاسبه کنید. ۲۰۲۱; پیش از چاپ [ Google Scholar ] [ CrossRef ]
وو، جی. وانگ، اچ. ژانگ، ام. Yu, Y. در مورد برنامه ریزی مسیر اجتناب از مانع در محیط های سه بعدی ناشناخته: یک چارچوب مبتنی بر سیال. ISA Trans. ۲۰۲۱ ، ۱۱۱ ، ۲۴۹-۲۶۴٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
رن، جی. ژانگ، جی. الگوریتم اجتناب از موانع خودمختار برای وسایل نقلیه سطحی بدون سرنشین بر اساس روش بهبود یافته مانع با سرعت. ISPRS Int. J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۶۱۸٫ [ Google Scholar ] [ CrossRef ]
آدیاتوف، او. Varol، HA یک الگوریتم جدید مبتنی بر RRT∗ برای برنامه ریزی حرکت در محیط های پویا. در مجموعه مقالات کنفرانس بین المللی IEEE 2017 در مکاترونیک و اتوماسیون، ICMA، تاکاماتسو، ژاپن، ۶ تا ۹ اوت ۲۰۱۷؛ جلد ۲۰۱۷، ص ۱۴۱۶–۱۴۲۱٫ [ Google Scholar ]
گامل، جی دی. سرینیواسا، اس اس. درختان آگاه دسته ای Barfoot، TD (BIT∗): برنامه ریزی بهینه مبتنی بر نمونه برداری از طریق جستجوی اکتشافی هدایت شده نمودارهای هندسی تصادفی ضمنی. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد رباتیک و اتوماسیون، سیاتل، WA، ایالات متحده آمریکا، ۲۶-۳۰ مه ۲۰۱۵٫ جلد ۲۰۱۵، ص ۳۰۶۷–۳۰۷۴٫ [ Google Scholar ]
باکدی، ع. هنتوت، ا. بوتامی، ح. مائودج، ع. هاچور، او. Bouzouia, B. برنامه ریزی و اجرای مسیر بهینه برای ربات های متحرک با استفاده از الگوریتم ژنتیک و کنترل منطق فازی تطبیقی. غارت. Auton. سیستم ۲۰۱۷ ، ۸۹ ، ۹۵-۱۰۹٫ [ Google Scholar ] [ CrossRef ]
شیونگ، سی. چن، دی. لو، دی. زنگ، ز. لیان، ال. برنامه‌ریزی مسیر چندین وسیله نقلیه دریایی مستقل برای نمونه‌برداری تطبیقی با استفاده از بهینه‌سازی کلونی مورچه‌ها مبتنی بر Voronoi. غارت. Auton. سیستم ۲۰۱۹ ، ۱۱۵ ، ۹۰-۱۰۳٫ [ Google Scholar ] [ CrossRef ]
کارامان، س. Frazzoli، E. الگوریتم های مبتنی بر نمونه برداری برای برنامه ریزی حرکت بهینه. Proc. بین المللی ربات جی. Res. ۲۰۱۱ ، ۳۰ ، ۸۴۶-۸۹۴٫ [ Google Scholar ]
اورمسون، سی. Simmons, R. رویکردهایی برای رشد RRT با سوگیری اکتشافی. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد ربات ها و سیستم های هوشمند، لاس وگاس، NV، ایالات متحده، ۲۷-۳۱ اکتبر ۲۰۰۳٫ جلد ۲، ص ۱۱۷۸–۱۱۸۳٫ [ Google Scholar ]
فرگوسن، دی. Stentz، A. RRT های هر زمان. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد ربات ها و سیستم های هوشمند، پکن، چین، ۹ تا ۱۵ اکتبر ۲۰۰۶٫ صص ۵۳۶۹–۵۳۷۵٫ [ Google Scholar ]
پالمیری، ال. کونیگ، اس. برنامه ریزی حرکت غیرهولونومیک مبتنی بر Arras، KO RRT با استفاده از بایاس مسیر هر زاویه. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد رباتیک و اتوماسیون، استکهلم، سوئد، ۱۶-۲۱ مه ۲۰۱۶؛ دوره ۱۳۹۵، صص ۲۷۷۵–۲۷۸۱٫ [ Google Scholar ]
برونر، ام. بروژمن، بی. شولز، دی. سلسله مراتبی برنامه ریزی حرکت زمین ناهموار با استفاده از روش نمونه گیری بهینه. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد رباتیک و اتوماسیون، کارلسروهه، آلمان، ۶ تا ۱۰ مه ۲۰۱۳٫ صص ۵۵۳۹–۵۵۴۴٫ [ Google Scholar ]
آکگون، بی. استیلمن، ام. نمونه‌برداری اکتشافی برای برنامه‌ریزی حرکت بهینه در ابعاد بالا. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد ربات ها و سیستم های هوشمند، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، ۲۵ تا ۳۰ سپتامبر ۲۰۱۱٫ صص ۲۶۴۰–۲۶۴۵٫ [ Google Scholar ]
اوت، م. Correll, N. C-FOREST: برنامه ریزی موازی کوتاه ترین مسیر با سرعت فوق خطی. IEEE Trans. ربات. ۲۰۱۳ ، ۲۹ ، ۷۹۸-۸۰۶٫ [ Google Scholar ] [ CrossRef ]
ریو، اچ. پارک، Y. RRT آگاه‌شده بهبود یافته* با استفاده از اسکلت‌سازی نقشه Gridmap برای برنامه‌ریزی مسیر ربات موبایل. بین المللی جی. دقیق. مهندس Manuf. ۲۰۱۹ ، ۲۰ ، ۲۰۳۳–۲۰۳۹٫ [ Google Scholar ] [ CrossRef ]
گامل، جی دی. Barfoot، TD; Srinivasa، SS Informed Sampling برای برنامه ریزی مسیر مجانبی بهینه. IEEE Trans. ربات. ۲۰۱۸ ، ۳۴ ، ۹۶۶-۹۸۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
سالزمن، او. Halperin، D. RRT مجانبی نزدیک به بهینه برای برنامه ریزی حرکت سریع و با کیفیت بالا. IEEE Trans. ربات. ۲۰۱۶ ، ۳۲ ، ۴۷۳-۴۸۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
نوریمبتوف، بی. آدیاتوف، او. Yeleu، S. برنامه ریزی حرکتی Varol، HA برای پهپادهای هیبریدی در محیط های شهری متراکم. در مجموعه مقالات کنفرانس بین المللی IEEE/ASME در زمینه مکاترونیک هوشمند پیشرفته، AIM، مونیخ، آلمان، ۳ تا ۷ ژوئیه ۲۰۱۷؛ صفحات ۱۶۲۷-۱۶۳۲٫ [ Google Scholar ]
لی، ی. کوی، آر. لی، ز. Xu, D. تقریب شبکه عصبی مبتنی بر برنامه ریزی حرکتی نزدیک به بهینه با محدودیت های کینودینامیک با استفاده از RRT. IEEE Trans. الکترون صنعتی ۲۰۱۸ ، ۶۵ ، ۸۷۱۸–۸۷۲۹٫ [ Google Scholar ] [ CrossRef ]
ژانگ، ز. تانگ، سی. Li, Y. برنامه ریزی مسیر نفوذ پهپاد پنهان بر اساس الگوریتم ستاره A پراکنده بهبود یافته. در مجموعه مقالات سومین کنفرانس بین المللی ICEICT 2020–IEEE در زمینه فناوری اطلاعات و ارتباطات الکترونیکی، شنژن، چین، ۱۳ تا ۱۵ نوامبر ۲۰۲۰؛ صص ۳۸۸-۳۹۲٫ [ Google Scholar ]
بسادا پورتاس، ای. د لا توره، ال. د لا کروز، جی.ام. De Andrés-Toro، B. برنامه ریز مسیر تکاملی برای پهپادهای متعدد در سناریوهای واقعی. IEEE Trans. ربات. ۲۰۱۰ ، ۲۶ ، ۶۱۹-۶۳۴٫ [ Google Scholar ] [ CrossRef ]
ژانگ، ایکس. Duan, H. یک الگوریتم تکامل دیفرانسیل محدود بهبود یافته برای برنامه ریزی مسیر جهانی وسایل نقلیه هوایی بدون سرنشین. Appl. محاسبات نرم. J. ۲۰۱۵ ، ۲۶ ، ۲۷۰-۲۸۴٫ [ Google Scholar ] [ CrossRef ]
یانگ، پی. تانگ، ک. لوزانو، جی. کائو، X. برنامه‌ریزی مسیر برای وسیله نقلیه هوایی بدون سرنشین به‌وسیله نقاط راه به طور جداگانه در حال تکامل. IEEE Trans. ربات. ۲۰۱۵ ، ۳۱ ، ۱۱۳۰-۱۱۴۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ون، ن. ژائو، ال. سو، ایکس. Ma, P. الگوریتم برنامه ریزی مسیر آنلاین پهپاد در یک محیط خطرناک ارتفاع کم. IEEE/CAA J. Autom. گناه ۲۰۱۵ ، ۲ ، ۱۷۳-۱۸۵٫ [ Google Scholar ] [ CrossRef ]
لی، دی. آهنگ، اچ. برنامه ریزی مسیر بهینه شیم، DH بر اساس spline-RRT∗ برای پهپادهای بال ثابت که در محیط های سه بعدی کار می کنند. در مجموعه مقالات کنفرانس بین المللی کنترل، اتوماسیون و سیستم ها، Gyeonggi-do، کره، ۲۲-۲۵ اکتبر ۲۰۱۴٫ صص ۸۳۵-۸۳۹٫ [ Google Scholar ]
وب، دی جی; ون دن برگ، جی. کینودینامیک RRT*: برنامه ریزی حرکت بهینه مجانبی برای روبات های با دینامیک خطی. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد رباتیک و اتوماسیون، کارلسروهه، آلمان، ۶ تا ۱۰ مه ۲۰۱۳٫ ص ۵۰۵۴–۵۰۶۱٫ [ Google Scholar ]
آریا، س. کوه، DM; نتانیاهو، NS; سیلورمن، آر. Wu, AY یک الگوریتم بهینه برای جستجوی تقریبی نزدیکترین همسایه در ابعاد ثابت. J. ACM ۱۹۹۸ , ۴۵ , ۸۹۱-۹۲۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ریش، RW; لاتون، جی. Hadaegh, FY معماری بازخوردی برای کنترل سازند. در مجموعه مقالات کنفرانس کنترل آمریکایی، شیکاگو، IL، ایالات متحده آمریکا، ۲۸-۳۰ ژوئن ۲۰۰۰٫ جلد ۶، ص ۴۰۸۷–۴۰۹۱٫ [ Google Scholar ]

شکل ۱٫ نمودار جریان و نمودار نتیجه الگوریتم FC-RRT *. در شکل، کادر سبز نشان دهنده سهم ۱، کادر زرد نشان دهنده مشارکت ۲، و کادر نارنجی نشان دهنده مشارکت ۳ است. در نمودار نتیجه مشاهده می شود که الگوریتم در این مقاله می تواند مسیری با ایمنی مسیر بالاتر برای رادار به دست آورد. و سایر مناطق تهدید غیر از RRT* می تواند.

شکل ۲٫ شماره ۱ تعیین محدودیت پرواز (نماد درست یا غلط) و هزینه پرواز fc را برای _گره های جدید بالقوه (گره های نارنجی) نشان می دهد. شماره ۲ نشان می دهد که گسترش گره جدید FC-RRT* تکمیل شده است. گره ها و لبه های مشکی درخت هایی هستند که ایجاد شده اند و گره آبی رنگ p _rand است.