یک روش تطبیق سلسله مراتبی برای شبکه های جاده برداری با استفاده از مثلث سازی دلونه

خلاصه

هدف اصلی تطبیق شبکه جاده ای بردار، شناسایی جاده های همنام از دو منبع داده متفاوت است. روش‌های قبلی معمولاً بر تطبیق شبکه‌های جاده‌ای با سیستم مختصات یکسان، اما به ندرت با سیستم‌های مختصات متفاوت یا ناشناخته تمرکز می‌کنند، که ممکن است منجر به انحرافات بی اهمیت و غیرسیستماتیک (به عنوان مثال، زاویه چرخش) بین اشیاء همنام شود. برای پر کردن این شکاف، این مطالعه یک روش تطبیق شبکه جاده‌ای سلسله مراتبی جدید را بر اساس مثلث‌سازی دلونی (DTRM) پیشنهاد می‌کند. ابتدا کل شبکه راه های شهری با استفاده از اصل سکته مغزی به سه سطح (L1، L2، L3) تقسیم می شود. سپس، مش های مثلثی از L2 ساخته می شوند و حداقل واحد تطبیق (MMU) در مش مثلثی به جای واحد سنتی “گره-قوس” برای اندازه گیری شباهت برای تطبیق L2 استفاده می شود. در آخر، یک راه حل تطبیق سلسله مراتبی که روش آرامش احتمالی و شباهت MMU را ادغام می کند برای شناسایی روابط تطبیق شبکه جاده سه سطحی به دست می آید. آزمایش‌های انجام‌شده در ووهان، چین و اوکلند، نیوزیلند، نشان می‌دهد که معیارهای تشابه MMU می‌توانند به طور موثر مقدار شباهت را با زوایای چرخش متفاوت محاسبه کنند، و DTRM دقت بالاتری نسبت به روش معیار احتمال-آرامش-تطبیق (PRM) دارد و می‌تواند به درستی بیشترین تطابق روابط را با دقت متوسط ۸۹٫۶۳% شناسایی کنید. این مطالعه یک چارچوب تطبیقی برای شبکه‌های جاده‌ای با سیستم‌های مختصات متفاوت یا حتی ناشناخته ارائه می‌کند و به یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری کمک می‌کند. آزمایش‌های انجام‌شده در ووهان، چین و اوکلند، نیوزیلند، نشان می‌دهد که معیارهای تشابه MMU می‌توانند به طور موثر مقدار شباهت را با زوایای چرخش متفاوت محاسبه کنند، و DTRM دقت بالاتری نسبت به روش معیار احتمال-آرامش-تطبیق (PRM) دارد و می‌تواند به درستی بیشترین تطابق روابط را با دقت متوسط ۸۹٫۶۳% شناسایی کنید. این مطالعه یک چارچوب تطبیقی برای شبکه‌های جاده‌ای با سیستم‌های مختصات متفاوت یا حتی ناشناخته ارائه می‌کند و به یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری کمک می‌کند. آزمایش‌های انجام‌شده در ووهان، چین و اوکلند، نیوزیلند، نشان می‌دهد که معیارهای تشابه MMU می‌توانند به طور موثر مقدار شباهت را با زوایای چرخش متفاوت محاسبه کنند، و DTRM دقت بالاتری نسبت به روش معیار احتمال-آرامش-تطبیق (PRM) دارد و می‌تواند به درستی بیشترین تطابق روابط را با دقت متوسط ۸۹٫۶۳% شناسایی کنید. این مطالعه یک چارچوب تطبیقی برای شبکه‌های جاده‌ای با سیستم‌های مختصات متفاوت یا حتی ناشناخته ارائه می‌کند و به یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری کمک می‌کند. و DTRM دقت بالاتری نسبت به روش محک احتمال-آرامش-تطبیق (PRM) دارد و می تواند به درستی بیشترین تطابق روابط را با دقت متوسط ۸۹٫۶۳ درصد شناسایی کند. این مطالعه یک چارچوب تطبیقی برای شبکه‌های جاده‌ای با سیستم‌های مختصات متفاوت یا حتی ناشناخته ارائه می‌کند و به یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری کمک می‌کند. و DTRM دقت بالاتری نسبت به روش محک احتمال-آرامش-تطبیق (PRM) دارد و می تواند به درستی بیشترین تطابق روابط را با دقت متوسط ۸۹٫۶۳ درصد شناسایی کند. این مطالعه یک چارچوب تطبیقی برای شبکه‌های جاده‌ای با سیستم‌های مختصات متفاوت یا حتی ناشناخته ارائه می‌کند و به یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری کمک می‌کند.

کلید واژه ها:

تطبیق شبکه جاده ای ; سوگیری غیر سیستماتیک مثلث سازی دلونی ; سلسله مراتبی ; یکپارچه سازی و به روز رسانی جاده ها

۱٫ معرفی

تطبیق داده‌های جغرافیایی که مجموعه‌های داده‌های مختلف را به هم متصل می‌کند و آن‌ها را قابل همکاری می‌سازد، به دلیل نیاز به استفاده از اطلاعات از منابع داده‌های مختلف، کاربردهای گسترده‌ای در تحلیل فضایی دارد [۱ ] . از یک طرف، مقادیر زیادی از داده های مختلف جغرافیایی را می توان به راحتی از دولت های فدرال، ایالتی و محلی یا شرکت های خصوصی به دست آورد. از سوی دیگر، شناسایی اشیاء متناظر یک گام اساسی در تشخیص تغییر و به روز رسانی تدریجی مداوم است. بنابراین، ویژگی های جدید را می توان به راحتی شناسایی کرد و مجموعه داده های ناهمگن را می توان با بهبود دقت های موقعیتی یا معنایی در یک محصول غنی شده ادغام کرد [ ۲ ].

شبکه های جاده ای بردار، نمایش دیجیتالی نقشه های راه هستند. وظیفه اصلی تطبیق شبکه‌های جاده‌ای، ایجاد روابط متناظر از جفت‌های جاده – شی است که همان بخش از یک جاده دنیای واقعی را در نقشه‌های راه ناهمگن نشان می‌دهند [ ۳ ، ۴ ]. این یک پیش نیاز مهم برای یکپارچه سازی شبکه جاده ها، تشخیص تغییرات و به روز رسانی داده ها است. تقاضا برای شبکه های جاده ای منطبق به دلیل به روز رسانی به موقع و مقرون به صرفه داده های شبکه جاده ای و کاربردهای پایین دستی گسترده آن (مثلاً محصولات ناوبری وسیله نقلیه) افزایش یافته است [۵ ] .

الگوریتم های متعددی برای حل مسئله تطبیق شبکه های جاده ای پیشنهاد شده است [ ۵ ، ۶ ، ۷ ، ۸ ، ۹ ]. هسته اصلی شبکه‌های جاده‌ای منطبق، ارزیابی شباهت دو گره یا ویژگی جاده مربوطه است. تشابه درجه مشابه دو ویژگی را کمیت می کند و مبنایی را برای شناسایی رابطه تطابق اشیاء همنام فراهم می کند [ ۳]]. متریک شباهت از نظر واحد تطبیق متفاوت است. در مطالعات قبلی، واحد تطبیق با بافت محلی محدود در اطراف گره‌ها یا بخش‌های جاده (یعنی همسایگان مرتبه اول) نشان داده می‌شود. شباهت های مبتنی بر فاصله (به عنوان مثال، فاصله هاسدورف و فاصله فریشه) این واحدهای تطبیق عمدتاً در این رویکردها در نظر گرفته می شوند [ ۶ ، ۷ ، ۸ ، ۹ ، ۱۰ ]. در همین حال، چندین محقق تلاش کرده اند تا عوامل متعددی (به عنوان مثال، طول، جهت، سینووسیت، و تعداد اتصالات توپولوژیکی) را برای بهینه سازی معیارها ادغام کنند [ ۴ ، ۱۱ ، ۱۲ ، ۱۳ ، ۱۴٫]. این مطالعات دقت تطابق شبکه راه ها را به میزان زیادی بهبود بخشیده است.

با این حال، اکثر الگوریتم‌های تطبیق موجود برای شبکه‌های جاده‌ای بر روی شبکه‌های تطبیق با سطوح مختلف جزئیات (LOD) یا شناسایی جاده‌های همنام با سیستم مختصات یکسان تمرکز می‌کنند [ ۱۱ ، ۱۵ ، ۱۶ ]. توجه کمی به تطبیق الگوریتم‌های سیستم‌های مختصات مختلف یا ناشناخته با دانش نویسندگان می‌شود [ ۵ ، ۱۷ ، ۱۸ ، ۱۹]. با توجه به فرآیندهای تکنولوژیکی مختلف تولید نقشه، انحرافات بزرگ (به عنوان مثال، افست و چرخش) ممکن است برای بخش‌های جاده‌ای همنام توسط تولیدکنندگان مختلف با استفاده از سیستم‌های مختصات مختلف رخ دهد. این پدیده به عنوان سوگیری غیر سیستماتیک نیز شناخته می شود. در زیر کارهای مربوط به تطبیق شبکه های جاده ای با سیستم های مختصات مختلف ارائه شده است.

چن و همکاران [ ۱۹ ] یک الگوریتم تطبیق الگوی نقطه‌ای تحت محدودیت‌های جغرافیایی (Geo-PPM) برای مکان‌یابی نقاط منطبق بین دو مجموعه داده شبکه جاده‌ای در سیستم‌های ناشناخته در سطح نقطه با در نظر گرفتن اتصال جاده، جهت جاده، و توزیع جهانی تقاطع‌های جاده و یافتن پیشنهاد کرد. تبدیل بین دو طرح از مجموعه نقاط نامزد. لوان و همکاران [ ۲۰ ] اسکلت جاده شهری را به عنوان یک ساختار جهانی استخراج کرد و از خوشه اتصال به عنوان یک ساختار محلی استفاده کرد. سپس از حداکثر الگوریتم زیرگراف مشترک برای ایجاد محتمل‌ترین رابطه تطابق بین گره‌ها استفاده شد و یک تبدیل وابسته برای حذف تأثیرات سیستم‌های مختصات مختلف ایجاد شد. سیریبا و همکاران [ ۱۷] الگوریتمی را ارائه کرد که اصلاحی از معیار ثبت فاصله تعمیم یافته هاوسدورف است که مستلزم یک فرآیند رتبه بندی تکراری است که از مجموعه ای از کمیت های آماری کیفی برای ارزیابی مطابقت بین دو مجموعه داده (پیکسل و شی) تشکیل شده است. با این حال، نتیجه تا حد زیادی به پارامترهای اولیه چرخش و مقیاس بندی بستگی دارد. یانگ و همکاران [ ۵] یک روش تطبیق مبتنی بر الگو را پیشنهاد کرد که شبکه محلی اطراف هر گره را به عنوان واحد تطبیق اصلی استخراج می‌کند و شباهت بین واحدهای تطبیق را با توجه به حداقل فاصله ویرایش جاده اندازه‌گیری می‌کند. تولید واحد تطبیق اولیه در قالب ساختار گره-قوس به تنظیم آستانه بستگی دارد. این مطالعات توجه قابل‌توجهی به اطلاعات ساختاری شبکه جاده‌ها داشتند و شروع به تغییر از عناصر محلی به واحدهای مقیاس بزرگ‌تر (مثلاً خوشه‌های اتصال/بخش) برای حذف تأثیرات سیستم‌های مختصات مختلف کردند. اصطلاح ساختار “گره-قوس” در این مطالعه برای اشاره به ساختاری استفاده می شود که با گسترش تعداد معینی قوس (گره) با یک گره به عنوان مرکز ساخته می شود.

هنگامی که سیستم مختصات مجموعه داده منبع به طور قابل ملاحظه ای با مجموعه داده هدف متفاوت است، ساختار گره-قوس نیز به طور قابل توجهی متفاوت خواهد بود. هنگام تطبیق چنین مجموعه‌های داده، روش‌های موجود مشمول محدودیت‌های زیر می‌شوند: (۱) تعیین آستانه فاصله بافر مناسب برای انتخاب نامزد مورد انتظار در مجموعه داده هدف دشوار است، زیرا کاندیداها ممکن است دارای یک افست غیرسیستماتیک بزرگ با بخش‌های جاده همنام خود باشند. تأثیر افست چرخش در تعیین آستانه شعاع بافر را نمی توان به طور کامل در نظر گرفت. (۲) دقت معیارهای شباهت در میان بخش‌های جاده‌ای همنام ممکن است زمانی که افست چرخش اتفاق می‌افتد بسیار کاهش یابد. در مطالعات قبلی، شباهت‌های میان ساختارهای “گره-قوس” بر اساس فاصله به راحتی تحت تأثیر افست غیر سیستماتیک قرار گرفت. ساختارها در توزیع فضایی گسسته بودند و شامل دو نوع عنصر ناهمگن (یعنی گره و قوس) بودند. استفاده از این عناصر ناهمگن برای بیان ارتباط فضایی بین جاده ها کافی نیست، که ممکن است شباهت ساختاری را تحت تأثیر قرار دهد.

برای پرداختن به محدودیت‌های ذکر شده، این مطالعه به دنبال ارائه یک روش تطبیق جاده سلسله مراتبی بر اساس مش مثلثی Delaunay برای حل تعصب غیر سیستماتیک تطبیق شبکه جاده‌ای در سیستم‌های مختصات مختلف و غلبه بر محدودیت ساختار گره-قوس است. اهمیت ساختاری مستلزم در شبکه راه با بیان ساختاری مش مثلثی مطابقت دارد. صرف نظر از مقیاس، مش مثلثی همیشه می تواند به طور موثر ساختار شبکه جاده را در سطوح مختلف به تصویر بکشد و ویژگی های تغییر ناپذیری چرخش را داشته باشد.

مشارکت های اصلی اصلی این مطالعه شامل موارد زیر است:

(۱): این مقاله اهمیت معناشناسی سلسله مراتبی شبکه های جاده های شهری را برجسته می کند و یک چارچوب تطبیق سلسله مراتبی برای شبکه های جاده ای ایجاد می کند. این چارچوب روش آرامش احتمال و رابطه مجاورت فضایی بین ساختارهای سلسله مراتبی را برای دستیابی به تطابق در زمینه سلسله مراتبی با استفاده از استراتژی کنترل لایه به لایه ترکیب می کند.
(۲): این مقاله یک الگوریتم جدید مبتنی بر ساختار “گره-منطقه” به جای ساختار “گره-قوس” برای سرکوب چرخش افست در تطابق سطح شبکه غیراسکلتی پیشنهاد می‌کند. شبکه جاده ای سطح غیراسکلتی به شبکه های مثلثی تبدیل شده است که توسط گره ها و بخش های طبیعی محدود شده است. حداقل واحد تطبیق (MMU) در مش های مثلثی به عنوان واحد محاسبه پایه استفاده می شود. بسته به مشخصه تغییر ناپذیری چرخش یک مثلث، شباهت بین MMU ها تطبیق شبکه جاده غیراسکلتی را برای غلبه بر مشکل زاویه چرخش هدایت می کند. رابطه تطابق بین رئوس مش های مثلثی با استفاده از روش آرامش احتمال جهانی شناسایی می شود.

ادامه این مقاله به شرح زیر سازماندهی شده است. بخش ۲ روش پیشنهادی را برای سنتز استراتژی تطبیق سلسله مراتبی و تطبیق شباهت بر اساس MMU شرح می دهد. بخش ۳ آزمایش های انجام شده با استفاده از سه مجموعه داده واقعی مختلف را توصیف می کند، نتایج را تجزیه و تحلیل می کند، و عواملی را که ممکن است بر عملکرد روش پیشنهادی تأثیر بگذارد، مورد بحث قرار می دهد. بخش ۴ این مطالعه را به پایان می رساند.

۲٫ روش

۲٫۱٫ چارچوب روش شناختی

همانطور که در شکل ۱ نشان داده شده استچارچوب پیشنهادی استراتژی تطبیق سلسله مراتبی و تطبیق شباهت MMU را ترکیب می کند. این یک فرآیند چهار مرحله ای است. ابتدا، چارچوب کل شبکه جاده شهری (Ω) را به سه سطح تقسیم می‌کند: جاده‌های اسکلتی (L1: Υ)، جاده‌های فریم مناطق فرعی (L2: Φ)، و بخش باقی‌مانده از جاده‌های فرعی منطقه به استثنای جاده‌های چارچوب. L3: χ = Ω – Υ – Φ). سپس، جاده‌های L2 با استفاده از مثلث‌سازی Delaunay محدود (CDT) به شبکه‌های مثلثی محدود شده توسط گره‌ها و بخش‌های جاده تبدیل می‌شوند. پس از آن، شباهت MMU در مش ها برای شناسایی رابطه تطبیق L2 محاسبه می شود. در نهایت، یک استراتژی سلسله مراتبی برای شناسایی رابطه تطبیق سه سطح شبکه جاده، به ویژه با استفاده از رابطه تطبیق در L2 برای استخراج رابطه جفت‌های عنصر در L3 اعمال می‌شود.۲۱ ]. در این مطالعه، MMU در مش های مثلثی به عنوان ساختار ناحیه-گره برای مقابله با مشکل سوگیری غیرسیستماتیک تولید شده توسط سیستم های مختصات مختلف معرفی و تفسیر می شود. در همین حال، برای در نظر گرفتن مقیاس های مختلف، شباهت MMU در چارچوب تطبیق سلسله مراتبی تعبیه شده است، که سپس تطابق اعمال شده در سطح غیراسکلتی را هدایت می کند.

در بخش های فرعی زیر توضیحات مفصلی مطابق با چهار مرحله ذکر شده در این چارچوب ارائه می شود.

۲٫۲٫ نسل سلسله مراتبی شبکه راه

فرآیند تولید سلسله مراتبی برای شبکه راه شامل سه مرحله است. ابتدا با شبیه سازی مکانیسم شناختی بینایی انسان، اسکلت شبکه جاده های شهری با استفاده از اصل سکته مغزی استخراج می شود [ ۲۲ ]. در اینجا، سکته مغزی به عنوان واحدهای عملکردی طبیعی یک شبکه تعریف می شود [ ۲۳ ]. با تجمیع بخش‌های جاده مطابق با ویژگی‌های مختلف، مانند نام خیابان‌ها یا زاویه بین بخش‌های جاده مجاور، که به عنوان اصل سکته مغزی شناخته می‌شود، ساخته می‌شود. طولانی ترین ضربه های k به عنوان L1 انتخاب می شوند. مقدار k با نسبت ۱۰٪ تعیین می شود و نحوه تعیین نسبت در بخش ۳٫۷ بحث شده است .

جاده هایی با اتصال گره ۱ به عنوان جاده های غیراسکلتی (L3) انتخاب می شوند. بگذارید NS تعداد ضربات، LS طول یک ضربه و T آستانه طول ضربه باشد. ΔNS ، تفاوت بین تعداد ضربات در مجموعه داده های منبع و هدف که طول آنها بیشتر از T است ، به صورت تعریف می شود.

Δناس=(ناسOتی-ناسDتی)،تی∈استی

(۱)

که در آن NS _OT تعداد ضربات با طول بیشتر از T در مجموعه داده منبع را نشان می دهد، NS _DT تعداد ضربات با طول بیشتر از T در مجموعه داده هدف را نشان می دهد، و S _T مجموعه ای از تمام طول های جاده در منبع است. و مجموعه داده های هدف حداقل آستانه طول ضربه به صورت C نشان داده شده و به صورت فرموله شده است

سی=مترمنn(تی)،Δناس=۰″Δناس”=۰

(۲)

سکته مغزی که طول آنها کمتر از C است نیز به عنوان L3 طبقه بندی می شوند، در حالی که جاده های باقی مانده به عنوان L2 طبقه بندی می شوند. تفاوت بین تعداد ضربه های با طول بیشتر از C در مجموعه داده های منبع و هدف باید ۰ باشد یا مشتق تفاوت باید ۰ باشد. بنابراین، تعداد ضربه های به دست آمده از L2 در مجموعه داده های منبع و هدف مشابه است. . این شرط پیش نیاز تطبیق است.

همانطور که در شکل ۲ نشان داده شده است، با توجه به اصل تولید سلسله مراتبی، یک نمونه از شبکه راه ابتدا به زیرمنطقه هایی تقسیم می شود که L1 را تشکیل می دهند. L1 نمایانگر اسکلت شبکه راه است. سپس، برای زیرمنطقه بالا سمت راست در L1، شبکه جاده های L2 و L3 تولید شده از شبکه جاده مبدا و شبکه جاده هدف به ترتیب نشان داده شده است. تفاوت بین شبکه جاده مبدأ و شبکه جاده هدف برای L1 ظریف، برای L2 متوسط و برای L3 آشکار است.

۲٫۳٫ ساخت و ساز مثلث سازی Delaunay توسط گره ها و بخش های جاده محدود شده است

در این زیر بخش، L2 که از گره ها و بخش های جاده تشکیل شده است به یک شبکه مثلثی تبدیل می شود. همانطور که در شکل ۳ الف نشان داده شده است، گوشه بالا سمت چپ داده های گره-قوس را نشان می دهد که باید مثلث شوند، شامل شش گره جاده A، B، C، D، E و F، و یک قطعه جاده AB. در غیاب قطعه AB، مثلث سازی همانطور که در شکل ۳ ب نشان داده شده است ساخته می شود. در این مطالعه، مثلث بندی باید تحت محدودیت گره ها و بخش ها انجام شود، همانطور که در شکل ۳ ج نشان داده شده است.

هنگامی که جاده های مقعر زیادی در مرز بلوک خیابان وجود دارد، همانطور که در شکل ۴ الف نشان داده شده است، شبکه مثلثی ایجاد شده ممکن است دارای چند مثلث باریک و کشیده باشد، همانطور که در شکل ۴ ب نشان داده شده است. در شکل ۵ الف، برخی از گره ها در داخل مرز تنها در یک طرف دارای شبکه مثلثی هستند زیرا مرز به عنوان یک محدودیت خارجی عمل می کند. این مش مغرضانه تأثیر زیادی بر روند تطبیق بعدی دارد. برای کاهش اثر مرزی، مش های مثلثی به صورت زیر بهینه می شوند:

(۱): بدنه محدب (M) تمام گره ها در جاده های چارچوب مجموعه داده های منبع و هدف محاسبه می شود.
(۲): بدنه محدب M با استفاده از یک آستانه فاصله معین گسترش می یابد تا بدنه محدب N جدید موازی با M به دست آید.
(۳): گره‌های تمام بخش‌های خط روی بدنه محدب N و گره‌ها و بخش‌های جاده‌های قاب در مجموعه داده شبکه جاده‌ای با هم مثلث‌بندی شده‌اند.

مثلث های بهینه شده با اعمال مراحل فوق در شکل ۵ ب نشان داده شده است. پس از آن، ساختار مشبک برای تطبیق شبکه جاده ساخته می شود.

۲٫۴٫ معیارهای تشابه بر اساس MMU

در این بخش، یک MMU به عنوان ساختار ناحیه-گره ساخته می شود. شباهت بین MMUها به شباهت بین زوج های مثلث اصلی بستگی دارد. ساختار مثلثی در فضا پیوسته است و شباهت آن تحت تأثیر زاویه چرخش قرار نمی گیرد. این می تواند ساختار فضایی شبکه جاده را به طور موثر مشخص کند.

MMU به عنوان مجموعه ای از مثلث ها با رئوس مشابه تعریف می شود و به صورت فرموله می شود

ممU={سیپ،تیاس}

(۳)

جایی که CP نشان دهنده گره مرکزی MMU است. فرض کنید M یک مدل مش باشد، M = { V , E , T } که V مجموعه ای از راس ها، E مجموعه ای از یال ها و T مجموعه ای از مثلث ها است. یک مثلث t , t = { v _i , e _i ; i = ۰ ، ۱ ، ۲ }، شامل سه رأس و سه یال است. یک یال e _i , e _i = { v _p, v _q , T _i } از نقاط انتهایی v _p و v _q و مجموعه مثلث های T _i که با آن محدود شده است تشکیل شده است. یک راس v _i , v _i = { x , y , E _i , T _i } با مختصات آن و یال های E _i و مثلث های T _i که حاوی آن هستند نشان داده می شود. TS مجموعه‌ای از مثلث‌های T _i را نشان می‌دهد که از CP سرچشمه گرفته‌اند، که به صورت فرموله شده است

تیاس={تیمن،سیپ∈تیمن آnد من=۱،۲،…،n}

(۴)

که در آن هر مثلث T _i دارای گره مرکزی CP است و این n مثلث در یک آرایش جهت عقربه های ساعت ذخیره می شوند. برای هر مثلث T ابتدا گره مرکزی CP و سپس دو راس آن را به ترتیب در جهت عقربه های ساعت ذخیره می کنیم. به عنوان نشان داده شده است

تی={سیپ،پ۱،پ۲}

(۵)

شکل ۶ یک MMU را نشان می‌دهد که در آن مجموعه مثلث‌های {a، b، c، d، e} که در مرکز نقطه P قرار دارند، توسط نقاط A، B، C، D و E احاطه شده‌اند.

TSM _P مجموعه ای از MMUهای تولید شده با استفاده از تمام گره های MMU با P به عنوان گره مرکزی را نشان می دهد و به عنوان فرمول (۶) تعریف می شود. S _P مجموعه تمام نقاط MMU _P را نشان می دهد .

تیاسمپ={ممUمن،پمن∈اسپ آnد من=۱،۲،…،n}

(۶)

شباهت بین MMU _P و MMU _O به صورت محاسبه می شود

اسمنمترOپ=۱n∑من=۱nمترآایکس∑j=1nاسمنمترمنj،تیمن∈تیاسO،تیj∈تیاسپ

(۷)

برای مثلث T _i ( Δآبسی) که در تیاسOو مثلث T _j ( ΔDEاف) که در تیاسپ، رئوس A و D، رئوس B و E و رئوس C و F با یکدیگر مطابقت دارند. شباهت بین دو زاویه ∠آ(تنظیم به آ) و ∠D(تنظیم به ایکس) است

منآ=cos3(π۲(۱-د(ایکس)))

(۸)

جایی که د(ایکس)=ه-۱۲ب۲(ایکس-ب)۲،ب=آپ/۳، و P به طور کلی روی ۵۰٪ تنظیم می شود. برای مثلث های T _i و T _j ، شباهت آنها اسمنمترمنjبه صورت زیر محاسبه می شود:

اسمنمترمنj=منآ∗منب∗منج۳

(۹)

فرض کنید P گره در مجموعه داده منبع باشد و O کاندیدایی باشد که با P در مجموعه داده هدف مطابقت دارد، سپس شباهت بین MMU _P و MMU _O از طریق پنج مرحله زیر محاسبه می شود:

(۱): MMU _P با P به عنوان گره مرکزی و TSM _O با O به عنوان گره مرکزی آماده می شوند.
(۲): MMU _P با محوریت P به O منتقل می شود تا MMU جدیدی به نام MMU _P_‘ به دست آید .
(۳): فاصله بین تمام گره ها در MMU _P_‘ و TSM _O برای تشکیل یک ماتریس فاصله محاسبه می شود. ما از ماتریس فاصله برای انتخاب گره ها در TSM _O استفاده می کنیم که در آن مجموع فاصله بین تمام گره ها در MMU _P_‘ و آنها کوچکترین است که به آن CPS _O می گویند . گره انتخاب شده قابل تکرار نیست.
(۴): MMU با O به _عنوان گره مرکزی و CPS _O به عنوان گره های اطراف بازسازی می شود که MMU _O نامیده می شود .
(۵): شباهت بین همه مثلث ها در MMU _P_‘ و MMU _O_‘ برای به دست آوردن یک ماتریس شباهت مثلث محاسبه می شود. در این ماتریس شباهت مثلثی، یک خط مورب از ماتریس با بیشترین مجموع مقادیر شباهت انتخاب می شود. شباهت بین MMU _P و MMU _O ، یعنی Sim _OP ، با مجموع مقادیر شباهت تقسیم بر تعداد مثلث ها نشان داده می شود. مطابقت بین گره های دو MMU نیز به دست می آید.

شکل ۷ نمونه ای از TSM _P و TSM _O را نشان می دهد که در آن خطوط قرمز به ترتیب نشان دهنده MMU _P و MMU _O هستند . پس از انتقال نقطه P به O ، MMU _P نیز با P حرکت می کند . ماتریس فاصله همه گره ها در MMU _P و همه گره ها در TSM _O محاسبه می شود و مجموعه ای از گره ها با کوچکترین مجموع فاصله از همه گره ها در MMU _P به دست می آید.

همانطور که در شکل ۷ نشان داده شده است، پنج جفت گره (A، S)، (B، T)، (C، M)، (D، U)، و (E، R) به دست آمده است. همانطور که در شکل ۸ نشان داده شده است، با O به عنوان گره مرکزی، از گره های اطراف (S، T، M، N، R) برای بازسازی MMU استفاده می شود . سپس، شباهت بین تمام مثلث‌ها در MMU _P و MMU _O برای بدست آوردن یک ماتریس شباهت مثلث، همانطور که در جدول ۱ نشان _داده شده است، محاسبه می‌شود.. مجموع مقادیر شباهت در تمام قطرهای ماتریس شباهت برای ایجاد بزرگترین قطر محاسبه می شود. ما میانگین شباهت MMU را با استفاده از مجموع شباهت های مورب ماتریس مشخص می کنیم. به عنوان مثال، مجموع شباهت خط مورب (av، bz، cy، dx، ew) برابر ۴٫۱۲ محاسبه می شود، سپس شباهت بین دو MMU O و P برابر ۴٫۱۲/۵ = ۰٫۸۲۴ است .

بر اساس شباهت بین MMU ها، نامزدهای مطابقت با هر MMU را می توان تعیین کرد. شکل ۹ نشان می دهد که پس از محاسبات قبلی، مطابقت بین هر گره، یعنی مطابقت بین (A, S), (B, T), (C, M) (D, N) و (E, R) ، و شباهت بین MMUهای آنها را می توان به دست آورد. بنابراین، شباهت بین MMUهای همسایه O و P برای بهینه سازی شباهت O و P و به دست آوردن یک نتیجه محاسبه شباهت که در سطح جهانی بهینه است، استفاده می شود. تکرار آرامش احتمالی بر روی شباهت MMU انجام می شود. در هر تکرار، احتمال تطبیق MMU _O و MMU _Pباید با استفاده از احتمال تطبیق (یعنی شباهت) زوج های مثلث زیردستان تنظیم شود. شباهت بین جفت‌های مثلث < i,j > در MMUها در تکرار t-ام Sim _ij را می‌توان با استفاده از مجموع وزنی احتمال این تکرار و میانگین احتمال تطبیق زوج‌های مثلث زیر آن به‌روزرسانی کرد. بدین ترتیب، شباهت بین O و P به عنوان به روز می شود

اسمنمترOپتی+۱=۱۲∗(اسمنمترOپتی+۱n∑من،j(من،j)∈اساسمنمترمنjتی)

(۱۰)

که در آن n تعداد زوج های مثلث در دو MMU است که در آنها مقدار یک عدد صحیح است. هر چه مقدار بزرگتر باشد، همگرایی سریعتر خواهد بود. متغیرهای i و j به ترتیب به ترتیب در جهت عقربه‌های ساعت مثلث‌های MMU _O و MMU _P با اعداد دنباله‌ای مطابقت دارند . ماتریس احتمال بالا تا زمان همگرایی تکرار می شود. جفتی که بیشترین احتمال تطابق را دارد، جفت تطبیق نهایی است.

شرایط توقف تکرار دو برابر است: (۱) تعداد تکرارها به آستانه مشخص شده (معمولا ۲۰) می رسد. (۲) تفاوت مقدار شباهت فعلی و مقدار شباهت آخرین تکرار کمتر از آستانه مشخص شده است (معمولا ۰٫۰۵). در طول فرآیند تکراری، شباهت مطابقت های صحیح به آرامی کاهش می یابد، در حالی که شباهت مطابقت های خطا به سرعت کاهش می یابد. شکاف واضحی در شباهت بین موارد تطبیق صحیح و اشتباه وجود دارد، سپس رابطه تطبیق نهایی بین MMUها با استفاده از شباهت بهینه شده تعیین می شود.

شکل ۱۰ چرخش معینی را بین دو MMU با O و P به عنوان گره های مرکزی نشان می دهد. برای انجام وظایف تطبیق با زاویه چرخش، پردازش زیر باید انجام شود:

(۱): شباهت تمام زوج های مثلث در دو MMU برای به دست آوردن یک ماتریس شباهت M محاسبه می شود .
(۲): دو بزرگ ترین مقدار شباهت در هر مورب ماتریس شباهت، ممنj،
(۳): ممنjک، انتخاب می شوند و مجموع دو مقدار که به صورت نشان داده می شود اسمنمترمنj، محاسبه می شود.
(۴): بزرگترین مقادیر شباهت اسمنمترمنjکه مقادیر شباهت را در مورب i-ام نشان می دهد ، به عنوان بهترین شاخص برای توصیف روابط تطبیق بین مثلث ها در دو MMU انتخاب می شود.
(۵): حداکثر مقدار شباهت ممنjدر مورب i انتخاب می شود و زاویه انحراف δ دو مثلث مطابق با مطابقت بین زوج مثلث < i,j > محاسبه می شود. سپس، MMU در مرکز P با استفاده از زاویه δ برای تولید یک MMU جدید، همانطور که در شکل ۱۱ نشان داده شده است، می چرخد . در نهایت، شباهت های بین دو MMU محاسبه می شود.

۲٫۵٫ شناسایی رابطه تطبیق با استفاده از استراتژی تطبیق سلسله مراتبی

رابطه فضایی جاده های همسایه در طول طبقه بندی نسبتاً پایدار است. ساختار جاده ای که اسکلت شهری را تشکیل می دهد می تواند به عنوان یک زمینه تطبیق سلسله مراتبی قابل اعتماد برای واحدهای تطبیق محلی استفاده شود. روابط تطبیقی از سطح بالا به سطح پایین شناسایی می شوند.

ابتدا، رابطه تطابق L1 مشخص می شود. قسمت مشترک اسکلت ها برای تعیین تطابقات خاصی از L1 ساخته شده است.

دوم، رابطه تطابق L2 شناسایی شده است. فرض کنید V _a { a _i , i ∈{ ۱ , ۲ , ۳ ,…, m }} و V _b { b _i , i ∈{ ۱ , ۲ , ۳ ,…, n }} مجموعه گره های L2 در مجموعه داده های منبع و هدف V _a دارای m گره است. V _b دارای n گره است. a _i نشان دهنده i است-مین گره در V _a و b _i نشان دهنده گره i- امین در Vb است ( b _i_, i ∈{ ۱ , ۲ , ۳ , …, n }). بر اساس معیارهای مشابهت MMU در بخش ۲٫۲ ، بخش ۲٫۳ و بخش ۲٫۴ ، مراحل تطبیق L2 به شرح زیر است:

(۱): بدنه محدب M تمام گره‌ها در V _a و Vb با استفاده از فاصله معینی محاسبه و گسترش می‌یابد (در اینجا مقدار فاصله روی ۹۰ متر تنظیم می‌شود) تا یک بدنه محدب جدید _N موازی با M بدست آید .
(۲): گره های لبه بدنه محدب N ، تمام گره های V _a و Vb و تمام بخش های جاده به عنوان محدودیت برای ایجاد دو مثلث استفاده می شوند که به صورت _S a _و Sb بیان _می شوند .
(۳): یک بافر دایره‌ای با نقطه _{a i به عنوان مرکز و یک شعاع معین تنظیم می‌شود و تمام گره‌ها در ناحیه بافر Vb به عنوان گره‌های منطبق با i} در _نظر گرفته می‌شوند و به عنوان M _{i ثبت}_{می‌شوند} .
(۴): روش ذکر شده در بخش ۲٫۴ برای محاسبه شباهت MMU همه گره‌ها با گره‌های a _i و Mi به‌طور متوالی، و روش آرامش احتمال برای به دست آوردن یک نتیجه شباهت بهینه جهانی استفاده می‌شود _.
(۵): مراحل ۳ و ۴ برای همه گره های V _a انجام می شود تا همه مطابقت ها در L2 مشخص شود.

سوم، رابطه تطابق L3 شناسایی شده است. L3 معمولاً پسوند L2 است. از این رو، اتصالات بین L2 و L3 به عنوان زمینه برای استخراج تطابق L3 بر اساس تطابق L2 استفاده می شود. بگذارید L _i جاده i -مین مجموعه داده منبع در L2 باشد و L _j جاده j -مین مجموعه داده هدف در L2 باشد . مراحل تطبیق L3 به شرح زیر است:

(۱): هر L _i دو نقطه پایانی دارد، Vi _۱ و Vi _۲ . جاده متصل در L3 به عنوان CL _i با دو نقطه پایانی CVi _۱ ، CVi _۲ ، و CVi _۱ در L _i نشان داده شده است . به طور مشابه، هر L _j دو نقطه پایانی دارد، Vj _۱ و Vj _۲ .
(۲): مطابق با نتایج تطبیق L2، اگر جفت های تطبیق ( Vi _۱ ، Vj _۱ ) و ( Vi _۲ ، Vj _۲ ) به دست آیند، آنگاه رابطه تطابق بین ( _Li ، Lj ₎ را می توان تعیین کرد. جاده متصل به L _j با CLj (j = 1,2, 3,…,k) مشخص می شود . CVj _۱ , CVj ۲ _دو نقطه پایانی L _j_{هستند و}CVj _۱ روی L _j قرار دارد .
(۳): اگر CL _i و CL _j دو شرط زیر را داشته باشند: ۱) CL _i و CL _j به ترتیب در یک سمت L _i و L _j هستند . ۲) موقعیت نسبی CVi _۱ در L _i نزدیکترین به موقعیت نسبی CVj _۱ در L _j است و اختلاف نباید بیشتر از ۲۰٪ باشد، سپس CVi _۱ با CVj _۱ مطابقت دارد .
(۴): اگر CVi _۲ و CVj _۲ به جاده های دیگر متصل نباشند، CVi _۲ با CVj _۲ مطابقت دارد و گره های همسان در همان لایه جاده قرار می گیرند.
(۵): مراحل ۱ تا ۴ تکرار می شوند تا زمانی که منطبق جدیدی وجود نداشته باشد.

همانطور که در شکل ۱۲ نشان داده شده است، road AB از L2 از مجموعه داده منبع است، و road QW از L2 از مجموعه داده هدف است. GF، CD، و EH از L3 از مجموعه داده منبع، و TR از L3 از مجموعه داده هدف است. با توجه به اینکه (A, Q) و (B, W) گره های تطبیق شناخته شده هستند، AB با QW مطابقت دارد. سه جاده GF، EH و CD به جاده AB متصل می شوند، جایی که گره های F، H و D در جاده AB قرار دارند. جاده TR به جاده QW، از جمله R متصل است. موقعیت نسبی نقاط F، H و D در جاده AB به ترتیب ۲۵، ۳۰، و ۷۶ درصد است. و R در ۲۸ درصد QW جاده قرار دارد. جاده های GF و CD در سمت چپ جاده AB، جاده EH در سمت راست جاده AB و جاده TR در سمت چپ جاده QW قرار دارد. GF و TR دو شرط را در مرحله ۳ برآورده می کنند. بنابراین، F با R مطابقت دارد. مطابق با مرحله ۴، G مطابقت با T برای G و T به جاده های دیگر متصل نیست.

۳٫ اجرا و آزمایش

۳٫۱٫ منطقه آزمایشی و داده ها

روش پیشنهادی با استفاده از زبان برنامه نویسی C++ پیاده سازی شده است. آزمایش‌ها روی رایانه‌ای انجام می‌شود که مجهز به پردازنده گرافیکی NVIDIA GeForce GTX 960 و Intel(R) Pentium(R) D 3.00GHz با ۳٫۵ گیگابایت رم است. محیط توسعه نرم افزار از Visual Studio 2010 و MapGIS 10 (Zondy، Wuhan، Hubei، چین) تشکیل شده است.

برای ارزیابی اثربخشی و عملکرد روش ما، از سه جفت شبکه جاده‌ای استفاده می‌شود. مناطق ۱ و ۲ از ووهان چین و منطقه ۳ متعلق به اوکلند نیوزلند است. هر جفت شبکه جاده ای از تولیدکنندگان داده های مختلف می آید. نقشه مبدا نشان دهنده شبکه جاده ای است که باید مطابقت داده شود و نقشه هدف نشان دهنده شبکه جاده ای است که برای مطابقت با نقشه مبدا استفاده می شود.

اول، انتخاب داده های تجربی تأثیر مقیاس را در نظر می گیرد. نقشه های مبدا و مقصد منطقه ۱ دارای مقیاس های یکسانی هستند، در حالی که نقشه های منطقه ۲ و ناحیه ۳ دارای مقیاس های متفاوتی هستند. این سه ناحیه در شکل ۱۳ ، شکل ۱۴ و شکل ۱۵ به روشی از همپوشانی فضایی نشان داده شده اند. شکل ۱۳ شبکه جاده ای جزئی انتخاب شده ووهان را با همان مقیاس نشان می دهد که در آن تفاوت بین داده های منبع و هدف کم است. شکل ۱۴ و شکل ۱۵داده های جاده های شهری ووهان یا اوکلند را با مقیاس های مختلف نشان می دهد. مجموعه داده های منبع و هدف در ساختار جهانی سازگار هستند. در مناطق محلی، مجموعه داده هدف دارای جاده های کوچکتر است. یعنی بخش بزرگی از روابط ۱:۰ وجود دارد و تفاوت‌های موجود در این داده‌ها ممکن است باعث ایجاد تفاوت قابل‌توجهی در واحد تطبیق اصلی-MMU و چالش‌های خاصی برای الگوریتم تطبیق شود. اطلاعات مربوط به گره های جاده، بخش های جاده، و سکته مغزی در سه منطقه آزمایشی در جدول ۲ نشان داده شده است .

دوم، الگوهای خیابان نیز هنگام انتخاب داده های تجربی در نظر گرفته می شوند. الگوهای خیابان های شهری نتیجه بسیاری از پدیده های متقابل در طول زمان است، مانند جغرافیا، محیط طبیعی و دگرگونی های اجتماعی-اقتصادی. در این فرآیند، چندین الگوی خیابانی معمولی به تدریج شکل می‌گیرند: شبکه‌های خیابانی شبکه‌ای (برنامه‌ریزی‌شده)، شبکه‌های خیابانی نامنظم (خود تکامل‌یافته)، و شبکه‌های خیابانی ترکیبی (ساختارهای برنامه‌ریزی‌شده و خود تکامل‌یافته همزیستی می‌کنند) [۲۴، ۲۵ ] .]. پارتیشن بندی سلسله مراتبی باید در سه ناحیه آزمایشی با استفاده از روش پیشنهادی ما انجام شود. برای منطقه ۱، پارتیشن بندی سلسله مراتبی نادیده گرفته می شود و محاسبه تطبیق مستقیماً به دلیل اندازه کوچک آن انجام می شود. ناحیه ۱ با R1 شماره گذاری می شود. منطقه ۲ به چهار زیرمنطقه با شماره R2، R3، R4 و R5 تقسیم می شود. منطقه ۳ به سه منطقه فرعی با شماره R6، R7 و R8 تقسیم می شود. هشت زیرمنطقه در شکل ۱۶ نشان داده شده است . R1، R2، R3 و R4 متعلق به شبکه های خیابانی نامنظم (خود تکامل یافته) هستند. R5 و R7 عمدتاً شبکه های خیابانی (برنامه ریزی شده) هستند. R6 و R8 عمدتاً شبکه های خیابانی ترکیبی هستند. هشت منطقه فرعی سه الگوی معمولی از خیابان های شهری را پوشش می دهند. بنابراین، اثربخشی مدل پیشنهادی ما با این هشت منطقه مورد بررسی قرار می‌گیرد.

۳٫۲٫ شاخص های ارزیابی مدل

سه شاخص ارزیابی برای ارزیابی کمی نتایج تطبیق مدل‌ها معرفی شده‌اند. آنها دقت ( P )، یادآوری ( R ) و امتیاز F1 ( F1 ) هستند.

دقت نشان دهنده دقت تطبیق در تطبیق اشیا است. به عنوان درصد جفت هایی که به درستی تطبیق داده شده اند در رابطه با تعداد کل جفت های منطبق تعریف می شود و به صورت نمایش داده می شود.

پ=تیپتیپ+افپ

(۱۱)

که در آن TP (مثبت واقعی) تعداد زوج های جاده ای است که به درستی مطابقت داده شده اند و FP (مثبت کاذب) تعداد جفت های جاده ای است که به اشتباه مطابقت داده شده اند. هر چه P -value به ۱ نزدیک‌تر باشد، ویژگی‌های تطبیق شناسایی شده توسط الگوریتم دقیق‌تر است.

یادآوری درصد جفت‌هایی است که به درستی تطبیق داده شده‌اند در رابطه با تعداد جفت‌های تطبیق واقعی و به صورت نمایش داده می‌شوند.

آر=تیپتیپ+افن

(۱۲)

که در آن FN (منفی کاذب) تعداد جفت های واقعی متناظر در دو مجموعه داده است که شناسایی نشده اند.

امتیاز F1 دقت و یادآوری را برای ارائه یک معیار واحد برای نشان دادن موفقیت واقعی مدل ما در مقایسه با PRM ترکیب می‌کند و به صورت زیر بیان می‌شود:

اف۱=۲∗پ∗آرپ+آر

(۱۳)

اثربخشی الگوریتم پیشنهادی با مقایسه آن با یک معیار ارزیابی می‌شود. در سال‌های اخیر، الگوریتم تطابق احتمال آرامش (PRM) در مطالعات تطبیق شبکه جاده‌ای استفاده شده است [ ۲ ، ۷ ، ۱۲ ، ۱۳ ، ۱۴ ]. بنابراین، به عنوان یکی از الگوریتم های نماینده، روش تطبیق (از این پس PRM) پیشنهاد شده توسط [ ۷ ] به عنوان معیار پذیرفته شده و تحت همان محیط آزمایشی در این مطالعه پیاده سازی شده است. در آزمایش های زیر برای راحتی کار مدل ما DTRM نامیده می شود. شرط پایانی برای تکرار PRM بر اساس مقدار تجربه (۰٫۰۰۰۵) تنظیم می شود [ ۲۶ ].

۳٫۳٫ ارزیابی عملکرد الگوریتم

ما عملکرد الگوریتم را با سه ناحیه آزمایشی (مناطق ۱-۳) ارزیابی می کنیم. به طور خاص، الگوریتم پیشنهادی ما برای تطبیق هشت زیرمنطقه و مقایسه نتیجه با رابطه تطبیق شناسایی شده دستی برای ارزیابی دقت الگوریتم استفاده می‌شود. جدول ۳ ، جدول ۴ و جدول ۵ نتایج آماری را ارائه می کنند.

شکل ۱۷ امتیاز F1 DTRM و معیار PRM را با شبکه های جاده های مختلف نشان می دهد. عدد روی محور افقی مربوط به هشت زیر منطقه (از R1 تا R8) است. امتیاز F1 DTRM بیشتر از ۸۵٪ است و بیش از نیمی از امتیاز F1 بیشتر از ۹۳٪ است که در R1 به ۹۸٫۶۸٪ می رسد.

همانطور که در جدول ۳ ذکر شده است، امتیاز F1 DTRM برای منطقه ۱ (R1) به ۹۸٫۶۸% می رسد که نشان می دهد DTRM در داده های جاده های مقیاس کوچک در همان مقیاس عملکرد خوبی دارد و می تواند نتایج تطبیق را به دقت بدست آورد. در جدول ۴ ، امتیاز F1 DTRM برای منطقه ۲ (جاده های جزئی در ووهان) بالای ۹۳٪ است (به جز R2 که کمی کمتر از ۸۸٫۲۳٪ است). در مقایسه با PRM، امتیاز F1 در سه زیر منطقه R2، R3 و R4 بالاتر از PRM است و امتیاز F1 از R5 کمی کمتر از PRM است. در جدول ۵، امتیاز F1 DTRM تقریباً ۸۶٪ در سه منطقه فرعی منطقه ۳ (اوکلند) است. این نشان می دهد که عملکرد DTRM در سه منطقه فرعی تقریباً یکسان است، بدون نوسان زیاد. در مقابل، عملکرد PRM در سه منطقه فرعی ناسازگار است. امتیاز F1 در R8 تنها ۸۲٫۹۶ درصد است که بسیار کمتر از DTRM است.

به طور کلی، امتیاز F1 DTRM از منطقه ای به منطقه دیگر متفاوت است و عمدتاً از همان روند معیار پیروی می کند. اکثر مناطق فرعی (۷۵٪) در هنگام استفاده از DTRM در مقایسه با وضعیت استفاده از PRM امتیاز F1 بالاتری دارند. از این رو، عملکرد DTRM تا حدی بهبود یافته است.

شکل ۱۸ تفاوت بین امتیازات F1 DTRM و PRM را نشان می دهد. در هشت منطقه آزمایشی، میانگین اختلاف امتیاز F1 بین DTRM و PRM 1.25 است (حداکثر مقدار ۳٫۹۱٪ و حداقل مقدار ۱٫۰۷٪ است). اختلاف امتیاز F1 شش مورد از این زیرمنطقه ها مثبت است و میانگین آن ۲٫۱۱ است. اختلاف امتیاز F1 بین دو زیر منطقه (R5 و R7) منفی است. برای زیرمنطقه های دارای مقادیر منفی، مقادیر مطلق کمتر از ۰٫۰۲ است که در محدوده خطای قابل قبولی قرار دارد. شکل A2 d و شکل A3b نشان می دهد که مطابقت های خطا (خطوط قرمز) عمدتاً در ناحیه غیر شبکه ای مناطق باریک توزیع شده است. دلیل کاهش دقت این دو مورد را می توان به صورت زیر توضیح داد: برای چنین مناطق باریک، رابطه تطبیق ایجاد شده در L1 محدود است. در تطبیق جاده هیبریدی پیچیده، بین پارامترهای الگوی شکاف وجود دارد. در حالی که الگوی خیابان ترکیبی باید در مرز بین الگوهای مختلف خیابان مورد استفاده قرار گیرد. چنین عملیاتی ممکن است بر دقت تطبیق تأثیر بگذارد و یکی از محدودیت‌های روش پیشنهادی در این مطالعه است. در طول این نوع عملیات، مبادله بین رابطه همسان سطح بالایی (یعنی L2) و شباهت این لایه (یعنی L3) باید بیشتر مورد مطالعه قرار گیرد.

به طور کلی، زمانی که با الگوهای مختلف شبکه‌های جاده‌ای مواجه می‌شوید، DTRM می‌تواند عملکرد بهتری نسبت به PRM داشته باشد و به درستی بیشترین روابط تطبیق را شناسایی کند (به طور متوسط ۸۹٫۶۳٪). شکل A1 ، شکل A2 و شکل A3 به ترتیب نتایج تطبیق هشت منطقه فرعی را برای مناطق ۱-۳ نشان می دهد، جایی که خط نارنجی نشان دهنده گره هایی است که به درستی تطبیق داده شده اند، و خط قرمز نشان دهنده گره هایی است که مطابقت نادرست دارند (پیوست A ) .

۳٫۴٫ تست چرخش در MMU

برای تأیید صحت و اثربخشی الگوریتم پیشنهادی ما، ابتدا باید استحکام MMU که توسط یک ساختار ناحیه-گره نشان داده شده در مواجهه با افست چرخش بررسی شود. زیرمنطقه تجربی R4 برای انجام تست چرخش در این بخش انتخاب شده است. اندازه‌های شباهت MMU (واحد ناحیه گره) در روش پیشنهادی ما و واحد خط گره در PRM تحت جابجایی‌های چرخش مختلف مقایسه می‌شوند.

ابتدا، DR به عنوان درجه تفاوت بین عنصر منبع و عنصر منطبق با هدف و تفاوت بین عنصر منبع و مجموعه تطبیق نامزد نامتناسب تعریف می شود، همانطور که در فرمول (۱۴) نشان داده شده است. هر چه DR بزرگتر باشد، نشانگر شباهت بر اساس واحد MMU بهتر خواهد بود و تشخیص رابطه تطبیق صحیح آسانتر است.

Dآر=۱n∑من=۱n(سمنمترr-سمنمترoمن)

(۱۴)

جایی که سمنمترrمقدار شباهت بین گره منبع و گره درست مطابقت شده آن را نشان می دهد. سمنمترoمنمقدار شباهت بین گره منبع و گره نامزد i- امین را نشان می‌دهد و n نشان‌دهنده تعداد نامزدهایی است که بیشترین n شباهت را با گره منبع تطبیق داده‌اند (به جز گره به‌درستی تطبیق داده شده).

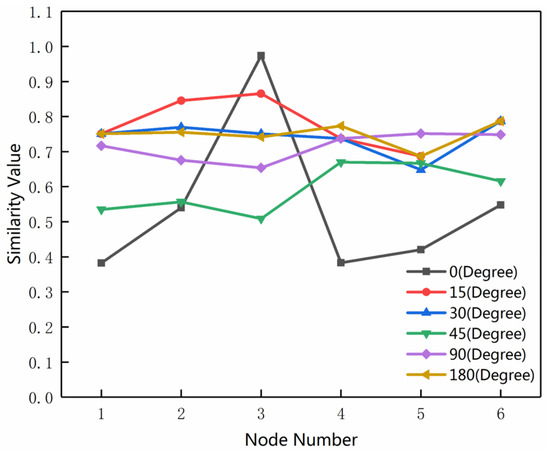
ده جفت گره در ناحیه R3 (توزیع مکان در شکل ۱۹ نشان داده شده است ) انتخاب می شوند و تفاوت DR بین DRTM و PRM بدون چرخش محاسبه می شود.

شکل ۲۰ منحنی مقایسه DR بین DRTM و PRM را با استفاده از ۱۰ جفت گره نشان می دهد. سطح متوسط DTRM به طور قابل توجهی بالاتر از PRM است. میانگین مقدار DR DTRM 0.64 است، در حالی که PRM 0.48 است. این نتیجه نشان می دهد که مقادیر شباهت MMU بالاتر از PRM است. این شرایط برای شناسایی جفت های صحیح عناصر با همان نام مساعد است.

پس از آن، مقادیر DR از ۱۰ جفت عنصر بین DTRM و PRM تحت زوایای چرخش مختلف مقایسه می‌شوند. نتایج آماری در شکل ۲۱ و شکل ۲۲ نشان داده شده است .

شکل ۲۱ نشان می دهد که وقتی زاویه چرخش ۰ درجه است، به این معنی که هیچ چرخشی رخ نمی دهد، DR PRM تقریبا ۰٫۵ است. یعنی مقدار شباهت بین گره ای که باید تطبیق داده شود و گرهی که به درستی تطبیق داده می شود با مقدار شباهت بین ویژگی که باید مطابقت داده شود و نامزد غیر همسان بسیار متفاوت است، که برای به دست آوردن تطابق صحیح مفید است. وقتی زاویه چرخش ۱۵ درجه باشد، DR تقریباً ۰٫۱ است. شباهت بین گره ای که باید تطبیق داده شود و گرهی که به درستی تطبیق داده شده است به اندازه شباهت بین گره ای که باید تطبیق داده شود و گره های ناهمسان آشکار نیست. با افزایش زاویه چرخش (۴۵-۱۸۰ درجه)، DRمقدار فقط به ۰٫۰۱ می رسد و مقداری منفی وجود دارد. این نتیجه نشان می دهد که پس از یک چرخش معین، مقدار شباهت بین گرهی که باید تطبیق داده شود و گره تطبیق صحیح در مقایسه با مقدار شباهت بین گرهی که باید تطبیق داده شود و گره ناهمسان به طور قابل توجهی کم است و PRM قادر به بدست آوردن یک مطابقت صحیح

همانطور که در شکل ۲۲ نشان داده شده است ، مقادیر DR ۱۰ جفت عنصر بدون توجه به زاویه چرخش، بالای ۰٫۵ است و DRمقادیر برخی از جفت عناصر بالاتر از ۰٫۷ و ۰٫۸ است. این نشان می دهد که هنگام استفاده از الگوریتم DTRM پیشنهادی ما، در مقایسه با مقدار شباهت گرهی که باید تطبیق داده شود، مقدار شباهت گره که با گره به درستی تطبیق داده شده است، همیشه تفاوت قابل توجهی را تحت زوایای چرخش مختلف حفظ می کند. این نشان می‌دهد که DTRM می‌تواند جفت‌های تطبیق صحیح را به طور موثر از منظر اندازه‌گیری شباهت بر اساس واحد MMU شناسایی کند و از استحکام قوی برخوردار است. علاوه بر این، نشان می دهد که MMU و معیارهای شباهت آن می توانند به طور موثر مقدار شباهت را در زوایای چرخش مختلف محاسبه کنند و بر محدودیت ساختار گره-قوس غلبه کنند.

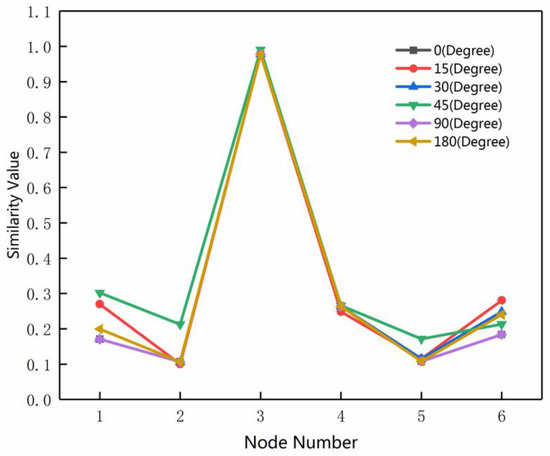
برای درک بیشتر تغییرات مقادیر شباهت بر حسب واحد تطبیق اصلی DTRM و PRM با زوایای چرخش مختلف، اولین جفت گره و شش گره با بالاترین مقادیر شباهت در مجموعه تطبیق نامزد انتخاب می‌شوند. نتایج PRM و DTRM در شکل ۲۳ و شکل ۲۴ نشان داده شده است . محور افقی نشان دهنده شاخص گره ها در مجموعه کاندید، محور عمودی نشان دهنده مقدار شباهت گره با گره در مجموعه کاندید است و گره ۳ گرهی است که به درستی مطابقت دارد.

همانطور که از شکل ۲۳ مشاهده می شود، زمانی که شبکه جاده دارای افست چرخشی نباشد (زاویه چرخش ۰ درجه است)، PRM به درستی گرهی را با بیشترین مقدار شباهت پس از تکرار آرامش احتمال مطابقت می دهد. با این وجود، مقدار شباهت در گره ۳ با سایر گره ها بسیار متفاوت است. هنگامی که شبکه جاده کمی می چرخد (زاویه چرخش ۱۵ درجه است)، اگرچه مقدار شباهت در گره ۳ همچنان بالاترین است، تفاوت بین گره ۳ و سایر گره ها قابل ملاحظه نیست. هنگامی که زاویه چرخش به افزایش ادامه می‌دهد، PRM دیگر نمی‌تواند گره‌های تطبیق صحیح را به درستی بدست آورد و تفاوت بین گره ۳ و سایر گره‌ها ملایم است. این نشان می‌دهد که در روش PRM هنگام مواجهه با داده‌های شبکه جاده‌ای با افست چرخشی، اندازه‌گیری شباهت بین واحدهای تطبیق اولیه نامعتبر می‌شود.

در شکل ۲۴ ، شش منحنی تقریباً با زوایای چرخش متفاوت یکسان هستند. مقدار شباهت محاسبه شده بر اساس MMU در گره ۳ بالاترین است و تفاوت قابل توجهی بین گره ۳ و سایر گره های کاندید وجود دارد. این نتیجه نشان می دهد که MMU ساختار ناحیه-گره ساخته شده با استفاده از الگوریتم پیشنهادی ما و متریک شباهت MMU موثر است.

۳٫۵٫ تست چرخش در شبکه راه

در این بخش، اعتبار و صحت DTRM پیشنهادی در این مقاله را تحت شرایط چرخش بر اساس شبکه جاده با مقایسه آن با PRM بررسی می‌کنیم. ما چرخش های زاویه ای (مثلاً ۱۵ درجه، ۳۰ درجه، ۴۵ درجه، ۹۰ درجه و ۱۸۰ درجه) را با استفاده از زیرمنطقه آزمایشی R4 انجام می دهیم. نتایج بدست آمده در شکل ۲۵ نشان داده شده است. هنگامی که زاویه چرخش به طور قابل توجهی بزرگ است (زیر ۱۵ درجه)، PRM هنوز هم می تواند یک نتیجه تطابق خوبی به دست آورد. با افزایش زاویه چرخش، نتیجه PRM به شدت کاهش می یابد. در ۹۰ درجه، دقت و فراخوانی کمتر از ۵٪ است. این نتیجه با نتیجه تابع اندازه گیری شباهت قبلی مطابقت دارد. DTRM می تواند عملکرد خوبی را با درجات چرخش مختلف نشان دهد. دقت و یادآوری تنها زمانی که زاویه چرخش افزایش می‌یابد اندکی کاهش می‌یابد، اما همچنان تقریباً ۹۰ درصد است. بنابراین، DTRM هنگام تطبیق داده ها با زوایای چرخش مختلف، عملکرد خوبی دارد.

نتیجه تطبیق زیر منطقه R3 با زاویه چرخش ۳۰ درجه برای انجام تجزیه و تحلیل بیشتر انتخاب شده است. شکل ۲۶ عدم تطابق DTRM را نشان می دهد. تعداد ناهماهنگی ها در مقایسه با تعداد عدم تطابق بدون چرخش فقط یک عدد افزایش می یابد ( شکل A1 در پیوست A ). این نشان می‌دهد که DTRM می‌تواند به خوبی تطبیق شبکه جاده‌ای را با افست چرخش مدیریت کند.

شکل ۲۷ تطابق خطای PRM را برای زیرمنطقه R4 با زاویه چرخش ۳۰ درجه نشان می دهد. می توان دریافت که گره هایی که با استفاده از PRM به اشتباه مطابقت دارند در نزدیکی مرز شبکه جاده متمرکز شده اند. تابع اندازه گیری شباهت PRM به فاصله فضایی و اتصالات توپولوژیکی جفت عنصر بستگی دارد. زمانی که فاصله مکانی عناصری با همین نام به دلیل جابجایی چرخش بسیار انحراف داشته باشد، بدست آوردن نتیجه صحیح برای PRM دشوار است.

۳٫۶٫ تجزیه و تحلیل حساسیت آستانه بافر

فاصله اقلیدسی بین ویژگی هایی با همین نام نیز با چرخش تغییر می کند. برای بازیابی دقیق‌تر کاندیدهای مطابق بالقوه، اندازه بافر باید به طور مناسب افزایش یابد. در این بخش حساسیت آستانه بافر با افزایش تدریجی اندازه بافر با افزایش زاویه چرخش بررسی می شود. سپس دقت و یادآوری دو روش محاسبه می‌شود تا تأثیر اندازه بافر بر نتایج تجربی آشکار شود.

همانطور که از شکل ۲۸ مشاهده می شود ، برای زوایای چرخش مختلف (مثلاً ۱۵ درجه، ۳۰ درجه، ۴۵ درجه، ۶۰ درجه، ۷۵ درجه و ۹۰ درجه)، زمانی که شعاع بافر نسبتاً کوچک است (یعنی ۲۰۰ متر)، دقت و یادآوری الگوریتم نسبتاً کم است. این ممکن است زمانی باشد که بافر بیش از حد کوچک باشد. عناصری با همان نام در مجموعه داده هدف در بافر نیستند و در نتیجه نرخ تطبیق پایینی دارد. با این حال، هنگامی که اندازه بافر به مقدار مشخصی می رسد و به افزایش خود ادامه می دهد، صرف نظر از استفاده از DTRM یا PRM، هیچ نوسان آشکاری در دقت و نرخ فراخوان وجود ندارد. این نشان می دهد که دو الگوریتم نسبت به اندازه بافر حساس نیستند و از استحکام خوبی برخوردار هستند.

علاوه بر این، اثر اندازه بافر بر عملکرد تطبیق PRM و DTRM در زوایای چرخش مختلف مقایسه می‌شود. با افزایش زاویه چرخش، دقت PRM به طور قابل توجهی کاهش می یابد. برای همان زاویه چرخش، با افزایش فاصله بافر، دقت کمی بهبود می‌یابد، اما همچنان به دقت PRM بدون زاویه چرخش نمی‌رسد. با افزایش زاویه چرخش، دقت DTRM به آرامی کاهش می یابد، در حالی که همچنان سطح بالایی (یعنی تقریباً ۸۰٪) حفظ می شود. همانطور که در شکل ۲۸ نشان داده شده استج، در یک زاویه ۴۵ درجه، هنگامی که شعاع بافر کمی افزایش می یابد، دقت DTRM به تدریج به سطح نسبتاً پایدار افزایش می یابد. زاویه چرخش عموماً تأثیرات متفاوتی بر دو روش تطبیق دارد. DTRM مقاومت خوبی در برابر زاویه چرخش نشان می دهد. هنگامی که زاویه چرخش افزایش می یابد، تأثیر زاویه چرخش بر دقت را می توان با افزایش مناسب شعاع بافر به طور موثری سرکوب کرد. به دلیل زاویه چرخش، استفاده از یک شعاع بافر ثابت ممکن است برخی از جفت‌های تطبیق نامزد را از دست بدهد و شعاع بافر برای انتخاب جفت‌های تطبیق نامزد باید افزایش یابد. افزایش مناسب شعاع بافر می تواند به طور موثر این مشکل را کاهش دهد. در مقابل، یک شعاع بافر بیش از حد بزرگ شده ممکن است جفت‌های تطبیق نادرستی را ایجاد کند که از نظر ساختار مشابه هستند و دقت تطابق را کاهش دهد.

۳٫۷٫ تاثیر آستانه طبقه بندی سلسله مراتبی

از آنجایی که ایجاد یک شبکه جاده سلسله مراتبی نقطه شروع روش پیشنهادی است، لازم است عقلانیت طبقه بندی تایید شود. بنابراین، این بخش توضیح می دهد که چگونه آستانه طبقه بندی انتخاب می شود. در مطالعات قبلی، شکستن سر/دم برای طبقه‌بندی سطوح مختلف شبکه جاده‌ها استفاده شد، زیرا در سازه‌های زنده چیزهای کوچک بیشتری نسبت به چیزهای بزرگ وجود دارد [ ۲۲ ]. آستانه طبقه بندی به مقادیر مختلف مطابق با الزامات برنامه پایین دستی مانند تعمیم نقشه برداری، پیش بینی جریان ترافیک و غیره تنظیم شد. در این مطالعه، نسبت ضربه های انتخاب شده در L1 در فرآیند تولید سلسله مراتبی بسیار مهم است. مطابق با نسبت مناسب، کتعیین می شود و طولانی ترین K ضربه به عنوان L1 انتخاب می شود. سپس سلسله مراتب شبکه های راه را می توان طبق مراحل بخش ۲٫۲ طبقه بندی کرد .

برای تعیین نسبت مناسب برای L1، از Dr و HitRate برای ارزیابی توزیع متفاوت ضربه های همسان هدف و ضربه های نامزد تحت نسبت های مختلف استفاده می شود. Dr به عنوان درجه تفاوت در شباهت بین ضربه منبع و ضربه منطبق با آن و تفاوت بین ضربه منبع و ضربه نامزد غیر همسان تعریف می شود که با فرمول (۱۵) نشان داده می شود.

Dr=مآایکس-Vمآایکس

(۱۵)

که در آن حداکثر شباهت بین stroke مطابق و ضربه منبع آن است که به عنوان مقدار مرجع نشان داده می شود. V شباهت بین استروک کاندید همسان و ضربه منبع آن است. هر چه Dr بزرگتر باشد، تفاوت بین ضربه همسان و غیر همسان آشکارتر است و دقت تطابق بالاتر است. به عبارت دیگر، یک نسبت مناسب باید ارزش Dr را تا حد امکان بزرگ نگه دارد.

HitRate به عنوان نسبت ضربه های نامزدی که در محدوده مقدار Dr مشخص شده قرار می گیرند به تمام ضربه های کاندید تحت شرایط مشخص تعریف می شود که در فرمول (۱۶) نشان داده شده است. در فرمول (۱۶) سه شرط وجود دارد. Con _b بیانگر شرایط اندازه بافر است. Con _p بیانگر شرایط نسبتی از طولانی ترین ضربات برای L1 است. Con _dr بیانگر شرایط یک مقدار Dr مشخص است . M نشان دهنده تعداد ضربه های نامزدی است که شرایط Con _b و Con _p را برآورده می کنند . نتعداد ضربه های نامزدی را نشان می دهد که شرایط Con _b ، Con _p و Con _dr را برآورده می کنند .

اچمنتیآرآتیه=ن[سیonپ∩سیonب∩سیonدr]م[سیonپ∩سیonب]

(۱۶)

منطقه ۲ به عنوان منطقه آزمایش در نظر گرفته می شود. اندازه بافر در Con _b روی ۵۰ متر و ۳۰۰ متر تنظیم شده است. نسبت Con _p برای L1 به ترتیب ۵%، ۱۰%، ۱۵%، ۲۰%، ۲۵% و ۳۰% است. رابطه توزیع بین HitRate و Dr در شکل ۲۹ نشان داده شده است . به عنوان مثال، B50_P5 سناریوی دو شرایط ترکیبی را نشان می دهد (اندازه بافر Con _b ۵۰ متر و نسبت Con _p ۵٪ است). وقتی Con _b روی ۵۰ متر تنظیم شود و مقادیر Con _p ۵٪ یا ۱۰٪ باشد، مقدار میانگین HitRateزمانی که Dr در محدوده (۰٫۵-۱] باشد، به ۰٫۹۲ می رسد ؛ که نشان می دهد بالای ۹۰٪ از ضربه های کاندید دارای تفاوت های هندسی آشکار با ضربه مشابه هدف هستند. مقدار HitRate به ۰ در محدوده Dr ۰-۰٫۵ نزدیک می شود، که نشان می دهد وجود دارد. تعداد بسیار کمی از ضربات کاندید که بسیار شبیه به ضربات همسان هدف هستند. به عبارت دیگر، نرخ تفاوت بین ضربات همسان هدف و ضربه های کاندید زمانی قابل توجه است که نسبت ها ۵٪ و ۱۰٪ باشد که برای به دست آوردن نتایج تطبیق صحیح مفید است. هنگامی که مقادیر Conp بزرگتر از ۱۰٪ باشد، مقدار HitRate در محدوده Dr ۰٫۵-۱ کاهش می یابد و در Dr افزایش می _یابد .محدوده ۰-۰٫۵ هنگامی که Con _b روی ۳۰۰ متر تنظیم می شود، روند توزیع مشابه زمانی است که Con _b روی ۵۰ متر تنظیم می شود، که نشان می دهد اندازه بافر تأثیر کمی بر میزان ضربه دارد . بنابراین، ۱۰٪ به عنوان نسبت انتخاب سطح اول L1 برای اطمینان از استحکام و دقت تطابق پیشنهاد می شود.

۴٫ نتیجه گیری

این مطالعه یک روش جدید برای تطبیق شبکه جاده‌ای سلسله مراتبی بر اساس مثلث‌سازی Delaunay (DTRM) و یک فرمول مسئله جدید برای غلبه بر مشکل تطبیق شبکه جاده‌ای با سوگیری غیرسیستماتیک در سیستم‌های مختصات مختلف ایجاد کرده است. مطابق با سلسله مراتب بصری انسان و مکانیسم شناختی منطقه ای، کل شبکه راه به سه سطح تقسیم می شود. رابطه تطبیق بالادست یک مرجع زمینه ای پایدار برای تجزیه و تحلیل تطبیق موجودیت های جاده پایین دست فراهم می کند، در نتیجه دقت تطبیق را بهبود می بخشد. به طور خاص، در چنین وظیفه تطبیق شبکه جاده ای، یک MMU جدید به جای واحد سنتی “گره-قوس” طراحی شده است. بر اساس ویژگی های چرخش ثابت مثلث ها، معیارهای تشابه مبتنی بر MMU به حل مشکل زاویه چرخش تطابق شبکه جاده غیراسکلتی کمک می کند. در مقایسه با روش‌های تطبیق سنتی مبتنی بر ویژگی‌های محلی، DTRM به کمیت‌سازی خاص هندسه جاده و خواص توپولوژیکی محدود نمی‌شود و همیشه ویژگی‌های سلسله مراتبی جهانی بهتری را در طول فرآیند تطبیق حفظ می‌کند. این مطالعه مسیر جدیدی را برای روش‌های تطبیق شبکه جاده‌ای سلسله مراتبی در مسیرهای مختلف باز می‌کند.

آزمایش‌ها با استفاده از مجموعه داده‌های واقعی ووهان، چین و اوکلند، نیوزلند برای تأیید کارایی رویکرد ما (DTRM) انجام می‌شوند. ما روش پیشنهادی خود را با روش PRM مقایسه می کنیم. نتایج به شرح زیر خلاصه می شود: (۱) هنگامی که با الگوهای مختلف شبکه راه (به عنوان مثال، پراکنده یا متراکم و شبکه یا شعاعی)، DTRM می تواند به دقت بالاتری نسبت به PRM معیار دست یابد و به درستی بیشترین روابط تطبیق را شناسایی کند (۸۹٫۶۳٪). به طور متوسط). (۲) از نظر شاخص های DR ، میانگین DRارزش DTRM به طور قابل توجهی بالاتر از PRM است. در مورد چرخش، معیارهای تشابه بر اساس MMU قدرت تمایز بهتری نسبت به شاخص سنتی در PRM دارند و برای شناسایی جفت‌های صحیح عناصر با همان نام مفیدتر هستند. نتایج همچنین نشان می‌دهد که ساختار MMU و متریک شباهت متناظر آن می‌تواند به طور موثر بر مشکل چرخش غلبه کند و از استحکام قوی برخوردار باشد. (۳) مقایسه شاخص‌های P و R DRTM و PRM نشان می‌دهد که PRM می‌تواند تطابق خوبی را زمانی که زاویه چرخش به طور قابل توجهی بزرگ است (زیر ۱۵ درجه) به دست آورد. با افزایش زاویه چرخش، P و Rمقادیر PRM به شدت کاهش می یابد. در مقابل، دقت و یادآوری DTRM فقط اندکی کاهش می‌یابد، اگرچه هر دو تقریباً ۹۰ درصد باقی می‌مانند. DTRM می تواند به طور موثر مشکل تطبیق جاده با زوایای چرخش مختلف را حل کند، با توجه به اینکه شاخص شباهت MMU نسبت به افزایش زاویه چرخش حساس نیست.

مدل توسعه‌یافته در این مطالعه برای یکپارچه‌سازی و به‌روزرسانی شبکه‌های جاده‌ای شهری و کاربردهای آن در سیستم‌های ناوبری مناسب است. این روش همچنین پتانسیل آن را دارد که در سایر بخش‌های شهری برای کاربردهای زیرساختی با اصلاحات بخش‌محور، مانند مدیریت عمومی [ ۲۷ ]، برنامه‌ریزی شهری [ ۲۸ ، ۲۹ ] و مدل‌سازی حمل‌ونقل [ ۳۰ ] اعمال شود.

در کارهای آینده، چندین موضوع نیاز به بررسی عمیق دارد. اول، در محل اتصال مناطق نامنظم و منظم، استحکام بر اساس تطبیق ساختار MMU نیاز به بررسی بیشتری دارد. دوم، هزینه زمانی کمتر از دقت روش‌های تطبیق شبکه جاده‌ای است. با افزایش حجم داده های تطبیق، مسئله عملکرد به طور فزاینده ای برجسته می شود. ثالثاً، معرفی یک روش یادگیری مبتنی بر جفت‌های تطبیق اولیه، موضوع جالبی برای حل مشکل تطبیق شبکه جاده‌ها است.

پیوست اول

شکل A1. نتایج تطبیق DTRM برای منطقه ۱ (R1).

شکل A2. نتایج تطبیق DTRM برای چهار منطقه فرعی منطقه ۲ (R2، R3، R4، و R5). ( الف ) نتیجه تطبیق R2، ( ب ) نتیجه تطبیق R3، ( ج ) نتیجه تطبیق R4، و ( د ) نتیجه تطبیق R5.

شکل A3. نتایج تطبیق DRTM برای سه منطقه فرعی منطقه ۳ (R6، R7، و R8). ( الف ) نتیجه تطبیق R6، ( ب ) نتیجه تطبیق R7، و ( ج ) نتیجه تطبیق R8.

منابع

Lei، TL ترکیب داده های جغرافیایی: یک رویکرد رسمی مبتنی بر بهینه سازی و پایگاه های داده رابطه ای. بین المللی جی. جئوگر. Inf. علمی ۲۰۲۰ . [ Google Scholar ] [ CrossRef ]
یانگ، بی. ژانگ، ی. Luan، X. یک رویکرد آرامش احتمالی برای تطبیق شبکه های جاده ای. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۳ ، ۲۷ ، ۳۱۹-۳۳۸٫ [ Google Scholar ] [ CrossRef ]
لی، ال. Goodchild، MF یک مدل بهینه سازی برای تطبیق ویژگی های خطی در ترکیب داده های جغرافیایی. بین المللی J. Image Data Fusion ۲۰۱۱ ، ۲ ، ۳۰۹-۳۲۸٫ [ Google Scholar ] [ CrossRef ]
والتر، وی. Fritsch، D. تطبیق مجموعه داده های مکانی: یک رویکرد آماری. بین المللی جی. جئوگر. Inf. علمی ۱۹۹۹ ، ۱۳ ، ۴۴۵-۴۷۳٫ [ Google Scholar ] [ CrossRef ]
یانگ، بی. لوان، ایکس. Zhang، Y. یک رویکرد مبتنی بر الگو برای تطبیق گره‌ها در شبکه‌های جاده‌ای شهری ناهمگن. ترانس. GIS ۲۰۱۴ ، ۱۸ ، ۷۱۸-۷۳۹٫ [ Google Scholar ] [ CrossRef ]
بیری، سی. کانزا، ی. صفرا، ای. Sagiv، Y. همجوشی اشیاء در سیستم های اطلاعات جغرافیایی. در مجموعه مقالات سی امین کنفرانس بین المللی پایگاه های داده بسیار بزرگ-جلد ۳۰; مورگان کافمن: تورنتو، ON، کانادا، ۲۰۰۴; صص ۸۱۶-۸۲۷٫ [ Google Scholar ]
آهنگ، دبلیو. کلر، جی.ام. Haithcoat، TL; دیویس، CH تطبیق ویژگی نقطه مبتنی بر آرامش برای ترکیب نقشه برداری. ترانس. GIS ۲۰۱۱ ، ۱۵ ، ۴۳-۶۰٫ [ Google Scholar ] [ CrossRef ]
صفرا، ای. کانزا، ی. ساگیو، ی. Doytsher, Y. تطبیق موقت شبکه های جاده ای بردار. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۳ ، ۲۷ ، ۱۱۴-۱۵۳٫ [ Google Scholar ] [ CrossRef ]
Min، D. ژیلین، ال. Xiaoyong، C. فاصله Hausdorff طولانی برای اشیاء فضایی در gis. بین المللی جی. جئوگر. Inf. علمی ۲۰۰۷ ، ۲۱ ، ۴۵۹-۴۷۵٫ [ Google Scholar ] [ CrossRef ]
تانگ، ایکس. لیانگ، دی. Jin, Y. روش تطبیق شی جاده خطی برای ادغام بر اساس بهینه سازی و رگرسیون لجستیک. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۴ ، ۲۸ ، ۸۲۴-۸۴۶٫ [ Google Scholar ] [ CrossRef ]
ژانگ، ام. منگ، L. الگوریتم گرا سکته مغزی محدود شده اصل کار و پیاده سازی برای تطبیق شبکه های جاده ای. Geogr. Inf. علمی ۲۰۰۸ ، ۱۴ ، ۴۴-۵۳٫ [ Google Scholar ] [ CrossRef ]
یانگ، ال. وان، بی. وانگ، آر. زو، ز. An، X. تطبیق شبکه جاده بر اساس محدودیت رابطه ساختاری سکته های سلسله مراتبی. Geomat. Inf. علمی دانشگاه ووهان ۲۰۱۵ ، ۴۰ ، ۱۶۶۱-۱۶۶۸٫ [ Google Scholar ]
ژائو، دی. Sheng, Y. تحقیق در مورد تطبیق خودکار شبکه های جاده ای بر اساس بهینه سازی جهانی. Acta Geod. کارتوگر. گناه ۲۰۱۰ ، ۳۹ ، ۴۱۶-۴۲۱٫ [ Google Scholar ]
ژانگ، جی. وانگ، ی. ژائو، دبلیو. یک روش آرامش احتمالی بهبود یافته برای تطبیق شبکه های جاده ای چند مقیاسی. بین المللی جی دیجیت. زمین ۲۰۱۸ ، ۱۱ ، ۱-۲۱٫ [ Google Scholar ] [ CrossRef ]
سباستین، ام. Devogele, T. تطبیق شبکه ها با سطوح مختلف جزئیات. Geoinformatica ۲۰۰۸ ، ۱۲ ، ۴۳۵-۴۵۳٫ [ Google Scholar ]
ولز، اس. یک رویکرد تکراری برای تطبیق نمایش های متعدد داده های خیابان. در مجموعه مقالات کارگاه مشترک ISPRS در مورد بازنمایی های متعدد و قابلیت همکاری داده های مکانی . دانشگاه اشتوتگارت: اشتوتگارت، آلمان، ۲۰۰۶; جلد XXXVI قسمت ۲/W40، صص ۱۰۱–۱۱۰٫ [ Google Scholar ]
سیریبا، DN; دالیوت، اس. ژئو ارجاع خودکار نقشه‌های موقت کاداستری غیرمکانی مرجع. Surv. Rev. ۲۰۱۲ , ۴۴ , ۱۴۲-۱۵۲٫ [ Google Scholar ] [ CrossRef ]
Saalfeld, A. Conflation گردآوری خودکار نقشه. بین المللی جی. جئوگر. Inf. سیستم ۱۹۸۸ ، ۲ ، ۲۱۷-۲۲۸٫ [ Google Scholar ] [ CrossRef ]
چن، سی سی; Knoblock، C. کلاهدوزان، م. تطبیق خودکار و کارآمد شبکه های جاده با ویژگی های فضایی در سیستم های هندسه ناشناخته. در مجموعه مقالات سومین کارگاه آموزشی STDBM، سئول، کره، ۱۱ سپتامبر ۲۰۰۶٫ [ Google Scholar ]
Luan، X. یک رویکرد مبتنی بر ساختار برای تطبیق اتصالات جاده‌ای با سیستم‌های مختصات مختلف. در مجموعه مقالات بیست و دومین کنگره ISPRS، ملبورن، استرالیا، ۲۵ اوت تا ۱ سپتامبر ۲۰۱۲٫ ص ۴۱-۴۶٫ [ Google Scholar ]
مسلم، ح. Türkay، G. یک رویکرد تطبیق چند مرحله ای جدید، مبتنی بر امتیاز برای درهم آمیختگی شبکه جاده ها در الگوهای جاده های مختلف. بین المللی J. Geo Inf. ۲۰۱۹ ، ۸ ، ۸۱٫ [ Google Scholar ]
جیانگ، بی. سلسله مراتب خیابان: اقلیتی از خیابان ها اکثریت جریان ترافیک را تشکیل می دهند. بین المللی جی. جئوگر. Inf. علمی ۲۰۰۹ ، ۲۳ ، ۱۰۳۳-۱۰۴۸٫ [ Google Scholar ] [ CrossRef ]
Thomson, RC مفهوم “سکته مغزی” در تعمیم و تحلیل شبکه جغرافیایی. در مجموعه مقالات دوازدهمین سمپوزیوم بین المللی در مورد مدیریت داده های فضایی، وین، اتریش، ۱۲ تا ۱۴ ژوئیه ۲۰۰۶٫ [ Google Scholar ]
Serge, S. Cities and Forms on Sustainable Urbanism ; چاپ معماری و ساختمان چین: پکن، چین، ۲۰۱۲٫ [ Google Scholar ]
ژن، دبلیو. یانگ، ال. کوان، م. زو، ز. وان، بی. ژو، اس. لی، اس. بله، ی. کیان، اچ. پان، ایکس. ثبت آنچه که چشمان انسان درک می‌کنند: یک رویکرد تولید سلسله مراتب بصری برای تقلید توجه بصری مبتنی بر برجسته‌سازی برای شبکه‌های خیابانی شهری شبکه‌ای. محاسبه کنید. محیط زیست سیستم شهری ۲۰۲۰ , ۸۰ , ۱۰۱۴۵۴٫ [ Google Scholar ] [ CrossRef ]
فینچ، AM; ویلسون، آرسی هنکوک، ER تطبیق مثلثات دلونی با آرامش احتمالی . Springer: برلین/هایدلبرگ، آلمان، ۱۹۹۵; صص ۳۵۰-۳۵۸٫ [ Google Scholar ]
یانگ، TR درک الگوهای رفت و آمد و تغییرات: تحلیل خلاف واقع در چارچوب پشتیبانی برنامه ریزی. محیط زیست طرح. ب مقعد شهری. علوم شهر ۲۰۲۰ . [ Google Scholar ] [ CrossRef ]
لیم، ال. یانگ، تی. ویالارد، ا. چن، اف. پپونیس، جی. مورفولوژی شهری و ساختار نحوی: بحثی در مورد رابطه اندازه بلوک با ادغام خیابان در برخی از سکونتگاه‌ها در پروونس. J. Space Syntax ۲۰۱۵ ، ۶ ، ۱۴۲-۱۶۹٫ [ Google Scholar ]
جیانگ، بی. کلارامونت، سی. تحلیل توپولوژیکی شبکه های خیابانی شهری. محیط زیست طرح. B طرح. طرح. ۲۰۰۴ ، ۳۱ ، ۱۵۱-۱۶۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مارشال، اس. گیل، جی. کروف، ک. تومکو، م. Figueiredo، L. مطالعات شبکه خیابانی: از شبکه ها تا مدل ها و بازنمایی آنها. شبکه تف کردن اقتصاد ۲۰۱۸ ، ۱۸ ، ۷۳۵-۷۴۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]

شکل ۱٫ چارچوب تطبیق سلسله مراتبی برای شبکه‌های جاده‌ای با استفاده از مثلث دلونی محدود (CDT).

شکل ۲٫ نمونه ای از تولید سلسله مراتبی یک شبکه جاده ای.

شکل ۳٫ مثلث سازی دلونی توسط گره ها و بخش ها محدود شده است. ( الف ) گره‌ها و بخش‌های ورودی، ( ب ) مثلث‌سازی با گره‌های بدون قطعه AB، و ( ج ) CDT با گره‌ها و قطعه AB.

شکل ۴٫ تصویر CDT با استفاده از گره ها و بخش ها. ( الف ) جاده مرزی مقعر و ( ب ) مثلث بلند باریک.

شکل ۵٫ بهینه سازی مثلث مرزی. ( الف ) مش مثلثی فقط در یک طرف حاشیه و ( ب ) نتایج بهینه سازی مثلثی. خط یکپارچه نشان دهنده نتیجه مثلث بندی اصلی است و خط نقطه چین نتیجه مثلث سازی پس از اضافه کردن نقاط بدنه محدب است.

شکل ۶٫ حداقل واحد تطبیق (MMU).

شکل ۷٫ ساختار مشبک مثلثی ( a ) TSM _P و ( b ) TSM _O.

شکل ۸٫ MMU با حرکت O به O به دست می آید .

شکل ۹٫ یک جفت MMU. ( الف ) MMU _P و ( ب ) MMU _O.

شکل ۱۰٫ MMU با افست چرخش. ( الف ) MMU _O و ( ب ) MMU _P.

شکل ۱۱٫ MMU پس از پردازش چرخشی. ( الف ) MMU _O و ( ب ) MMU _P پس از چرخش.

شکل ۱۲٫ شناسایی رابطه تطبیق برای L3.

شکل ۱۳٫ جفت های شبکه جاده ای در مقیاس مشابه از شهر ووهان (منطقه ۱).

شکل ۱۴٫ جفت های شبکه جاده ای در مقیاس های مختلف از شهر ووهان (منطقه ۲).

شکل ۱۵٫ جفت های شبکه جاده ای در مقیاس های مختلف از شهر اوکلند (منطقه ۳).

شکل ۱۶٫ هشت زیرمنطقه آزمایشی ( a ) R1، ( b ) R2، ( c ) R3، ( d ) R4، ( e ) R5، ( f ) R6، ( g ) R7، و ( h ) R8.

شکل ۱۷٫ امتیاز F1 از DTRM و PRM در هشت ناحیه (مناطق ۱-۸).

شکل ۱۸٫ تفاوت امتیاز F1 بین DTRM و PRM در هشت زیر منطقه آزمایشی.

شکل ۱۹٫ توزیع ۱۰ جفت گره با همین نام.

شکل ۲۰٫ DR DTRM و PRM.

شکل ۲۱٫ DR از ۱۰ جفت عنصر با همان نام تحت زوایای چرخش مختلف با استفاده از PRM.

شکل ۲۲٫ DR از ۱۰ جفت عنصر با همان نام تحت زوایای چرخش مختلف با استفاده از DTRM.

شکل ۲۳٫ منحنی شباهت شش جفت عنصر با همان نام تحت زوایای چرخش مختلف پس از تکرار آرامش تکراری با استفاده از PRM.

شکل ۲۴٫ منحنی های شباهت شش جفت گره با همان نام تحت زوایای چرخش مختلف پس از تکرار آرامش احتمالی با استفاده از DTRM.

شکل ۲۵٫ دقت و فراخوانی PRM و DTRM با زوایای چرخش مختلف.

شکل ۲۶٫ عدم تطابق با استفاده از DTRM با زاویه چرخش ۳۰ درجه.

شکل ۲۷٫ عدم تطابق با استفاده از PRM با زاویه چرخش ۳۰ درجه.

شکل ۲۸٫ دقت و فراخوانی PRM و DTRM با اندازه های مختلف بافر و زوایای چرخش. ( الف ) ۱۵ درجه، ( ب ) ۳۰ درجه، ( ج ) ۴۵ درجه، ( د ) ۶۰ درجه، ( e ) ۷۵ درجه، و ( f ) ۹۰ درجه.

شکل ۲۹٫ HitRate و Dr تحت شرایط مختلف.

ونوس نصیرفام

11 فوریه 2023

مقالات