ما روش‌های مختلف تطبیق را برای متمایز ساختن تغییرات ساختمان از جایگزین‌ها بر اساس هندسه‌های ردپای ساختمانی چند زمانی از مدل‌های شهر سه بعدی مقایسه می‌کنیم. ردپاهای ارجاع دستی تغییرات ساختمان برای تعیین اینکه کدام آستانه برای تمایز مناسب است استفاده شد. علاوه بر این، از آنجایی که داده‌های زیرزمینی LoD1 (سطح جزئیات ۱) بسیار دقیق است، انحراف‌های موقعیت به‌طور تصادفی ایجاد شده اضافه شد تا امکان انتقال به داده‌های کمتر مطابقت داده شود. به منظور ایجاد یک انحراف موقعیت تعریف شده، یک روش جدید توسعه داده شد. این امکان تعیین اثرات انحراف موقعیت بر دقت را فراهم می کند. بنابراین، تعیین مناسب بودن این روشها برای دستکاری داده‌ها از منابع سطوح مختلف تعمیم (تطبیق در مقیاس متقابل) تمرکز این کار نیست. به تفصیل، روش‌های “نسبت مساحت مشترک”، “نسبت مرز مشترک”، “فاصله هاسدورف” و “PoLiS” (متریک مبتنی بر بخش‌های چندضلعی و خطی) مقایسه شدند. علاوه بر این، یک رویه مبتنی بر خط توسعه یافته را توسعه دادیم که آن را «نسبت مرزی تقاطع» نامیدیم. نشان داده شد که این روش نسبت به روش های تطبیق قبلی برای انحرافات موقعیت کوچک قوی تر است. علاوه بر این، ما به این سوال پرداختیم که آیا یک تابع حداقل در فاصله PoLiS و Hausdorff برای تمایز بین اصلاح و جایگزینی مناسب‌تر است. نشان داده شد که این روش نسبت به روش های تطبیق قبلی برای انحرافات موقعیت کوچک قوی تر است. علاوه بر این، ما به این سوال پرداختیم که آیا یک تابع حداقل در فاصله PoLiS و Hausdorff برای تمایز بین اصلاح و جایگزینی مناسب‌تر است. نشان داده شد که این روش نسبت به روش های تطبیق قبلی برای انحرافات موقعیت کوچک قوی تر است. علاوه بر این، ما به این سوال پرداختیم که آیا یک تابع حداقل در فاصله PoLiS و Hausdorff برای تمایز بین اصلاح و جایگزینی مناسب‌تر است.
کلید واژه ها:
تشخیص تغییر ساختمان ; الگوریتم های تطبیق ; داده های برداری ; رد پا ؛ انحراف موقعیت
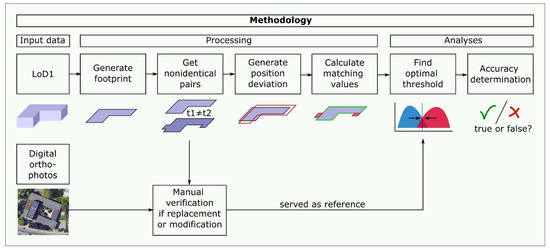
۱٫ مقدمه
۱٫۱٫ انگیزه
در دسترس بودن رو به رشد داده های مکانی با وضوح بالا، و به ویژه آنهایی که حاوی ساختمان های جداگانه هستند، منجر به استفاده روزافزون از چنین داده هایی در زمینه های مختلف شده است [ ۱ ، ۲ ، ۳ ]. تغییرات در انبار ساختمان برای بسیاری از کاربردها از اهمیت ویژه ای برخوردار است، زیرا آنها تأثیر توسعه گذشته را در یک زمینه معین نشان می دهند [ ۴ ، ۵ ، ۶ ]. داده های مربوط به چنین تغییراتی به درک کلی ما کمک می کند: می توان از آن به عنوان داده های ورودی برای مدل های پیش بینی استفاده کرد و به طور کلی به تصمیم گیری در مورد استفاده از زمین کمک می کند [ ۷ ]. مدل‌های شهری دقیق و به‌روز را می‌توان با استفاده از داده‌های سنجش از دور، مانند تصاویر هوایی/ماهواره‌ای یا ابرهای نقطه‌ای ایجاد کرد.۸ ، ۹ ]. با طبقه‌بندی داده‌ها، ساختمانها را می‌توان با اطلاعات تصویری یا ساختار آنها شناسایی کرد و امکان ردیابی تغییرات را در سطح اشیاء منفرد فراهم کرد [ ۱۰ ، ۱۱ ، ۱۲ ]. تشخیص اشیاء با استفاده از ابرهای نقطه LiDAR انجام می‌شود که منجر به مشتق‌سازی هندسه برداری ساختمانها می‌شود [ ۱۳ ]. بسته به نرخ نمونه برداری سنسور (تراکم نقطه)، جابجایی های موقعیتی در هندسه های برداری مشتق شده وجود دارد. بنابراین، تشخیص تغییر مبتنی بر برداری برای بسیاری از انواع داده‌های اولیه مهم است، چه هندسه‌های خودکار یا دستی بررسی‌شده.
چندین مطالعه تشخیص تغییر را با استفاده از محصولات ورودی تعمیم یافته مختلف بررسی کرده اند [ ۱۴ ، ۱۵ ، ۱۶ ، ۱۷ ، ۱۸ ، ۱۹ ]. با ترکیب چنین محصولاتی با اطلاعات کاداستر، می توان به طور قابل توجهی قدرت و سودمندی مدل ها را افزایش داد [ ۲۰ ، ۲۱ ، ۲۲ ]. با این حال، حتی داده‌های ساختمان از یک ارائه‌دهنده واحد می‌تواند در طول زمان از نظر هندسه انتخابی یا مدل‌سازی قطعات ساختمان متفاوت باشد، که ممکن است منجر به تغییرات غیرواقعی گسترده شود [ ۲۳ ].]. ارائه دهندگان رسمی همچنین به طور مداوم مدل های داده ها و فرآیندهای بررسی خود را بهبود می بخشند، نه تنها برای ارائه داده های با کیفیت بهتر و دقیق تر، بلکه برای پاسخگویی به تقاضاهای رو به رشد مشتریان و ایجاد یک پایگاه داده هماهنگ برای فعال کردن نظارت ملی [ ۲۴ ، ۲۵ ، ۲۶ ]. ، ۲۷ ]. اگرچه داده‌ها قطعاً در طول زمان از بسیاری جهات بهبود یافته‌اند، هر تغییری در فرآیند اکتساب می‌تواند منجر به تغییرات غیر واقعی شود، که به ندرت در خود داده‌ها مستند شده است [ ۲۸ ].
نظارت بر انبار ساختمان در طول زمان مستلزم تجزیه و تحلیل متمایز تغییرات، مانند ساخت و ساز جدید، تخریب، جایگزینی یا اصلاح ساختمان (به عنوان مثال، تخریب جزئی یا گسترش) است. با این حال، به ویژه دشوار است که بین ساختمان های اصلاح شده و جایگزین شده تمایز قائل شویم، زیرا در هر مورد تغییری در هندسه رخ داده است. تجزیه و تحلیل تغییرات دقیق مکانی به طور فزاینده ای تنها بر اساس هندسه های برداری انجام می شود، مانند ردپای بررسی شده از کاداسترهای زمین یا ساختمان های سه بعدی از مدل های سطح شهر (LoD) [ ۲۹ ، ۳۰ ، ۳۱ ]. در همین حال، چنین مجموعه داده های LoD به طور منظم به روز می شوند و بنابراین می توانند برای نظارت استفاده شوند [ ۳۲ ].
۱٫۲٫ هدف مطالعه
هنگام مقایسه هندسه های برداری داده های ساختمان، نسبت مساحت مشترک ( CAR ) [ ۳۳ ، ۳۴ ، ۳۵ ] یا نسبت مرز مشترک ( CBR ) [ ۳۶ ، ۳۷ ] برای شناسایی جفت های شی منطبق بر اساس استفاده می شود. از چند ضلعی های دو بعدی این روشها بسته به داده‌های اساسی و موضوع مورد بررسی، دقت‌های بسیار متفاوتی دارند [ ۳۸ ]. علاوه بر این، معیارهایی مانند فاصله Hausdorff ( HDD ) [ ۳۹ ] یا مقایسه چند ضلعی یا بخش های خطی ( PoLiS ) [ ۱۴ ] برای تعیین تغییرات در چند ضلعی های ساختمانی استفاده می شود. مقاله آوبلج [۱۴ ] قبلاً بررسی کرده است که چگونه ترجمه، چرخش و مقیاس بندی بر HDD ، PoLiS و فاصله Chamfer تأثیر می گذارد.
در این مقاله، بررسی می‌کنیم که چگونه این روشها برای تشخیص ساختمانهای اصلاح‌شده و جایگزین شده بر اساس هندسه‌های برداری مناسب هستند و چگونه انحراف موقعیت بر نتایج تأثیر می‌گذارد. در برخی موارد، چندین ناحیه تقاطع برای یک جفت شی اتفاق می‌افتد، جایی که عبارات مربوط به کل جفت شی ناکافی است. بنابراین، ما یک روش تطبیق مبتنی بر خط توسعه یافته را توسعه داده‌ایم، که با آن می‌توان چندین ناحیه تقاطع را به صورت جداگانه ارزیابی کرد، که آن را نسبت مرزی تقاطع ( IBR ) نامیده‌ایم.
علاوه بر این، یک سوال مهم این است که چگونه انحراف موقعیت بر دقت رویه های تطبیق تأثیر می گذارد. بنابراین، ما یک روش جدید برای ایجاد انحرافات موقعیت تعریف شده ایجاد کرده‌ایم.
به طور خاص، سه سوال زیر را در نظر می گیریم:
-
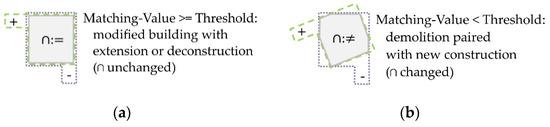
سوال تحقیق ۱ (RQ1): چه دقت و آستانه ای را می توان برای رویه های تطبیق CAR ، CBR ، HDD ، PoLiS و IBR برای تمایز بین ساختمان های اصلاح شده و جایگزین شده در هنگام تشخیص تغییرات در ردپای ساختمان انتظار داشت؟ در مورد CAR ، CBR و IBR ، انتظار داریم آستانه هایی بین ۵۰ تا ۷۰ درصد بر اساس مفروضات روتزینگر [ ۳۸ ] باشد.
-
سوال تحقیق ۲ (RQ2): هنگام تمایز بین ساختمان های تغییر یافته و جایگزین شده، آیا تابع حداقل برای معیارهای HDD و PoLiS مناسب تر از تابع حداکثر است ؟ از آنجایی که به هر حال ساختمانهای اصلاح‌شده به خوبی با هم مطابقت ندارند، بسته به میزان اصلاح، فرض می‌کنیم که یک تابع حداقلی برای تمایز بین ساختمانهای اصلاح‌شده و جایگزین شده بهتر است.
-
سوال تحقیق ۳ (RQ3): چگونه انحراف موقعیت بر دقت تأثیر می گذارد؟ ما فرض می‌کنیم که رویه‌های تطبیق CBR و IBR به احتمال زیاد نتایج نادرستی برای انحرافات موقعیت بزرگتر ایجاد می‌کنند، زیرا مقادیر تحمل این روشها اغلب منجر به عدم تطابق می‌شوند.
۲٫ مواد و روشها
در این بخش ابتدا گردش کار کلی روش شناسی مطالعه خود را نشان می دهیم. سپس یک نمای کلی از داده های ورودی استفاده شده، انواع مختلف تغییرات و روش های تطبیق بررسی شده ارائه می دهیم. علاوه بر این، ما نشان می‌دهیم که چگونه آستانه‌های بهینه تعیین شده‌اند، و چگونه انحراف موقعیت چندضلعی‌ها ایجاد شده است. نمودار گردش کار به عنوان جهت گیری برای ساختار این مطالعه عمل می کند ( شکل ۱ ).
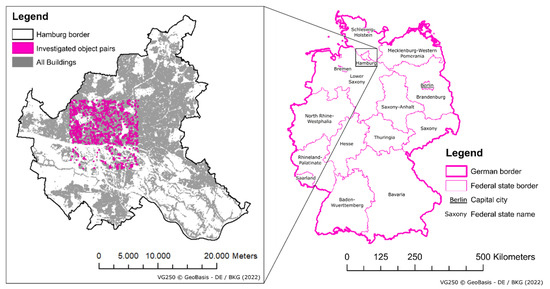
۲٫۱٫ مطالعه موردی و داده های ورودی
برای مطالعه خود، از داده های LoD1 (سطح جزئیات ۱) در قالب CityGML برای شهر هامبورگ به عنوان مبنای داده استفاده کردیم. در مورد داده های LoD1، ساختمان ها به صورت هندسه بلوک نشان داده می شوند. به عنوان مثال، هیچ جزئیات، مانند شکل سقف یا شیروانی، نشان داده نشده است. داده ها فقط حاوی ردپای اکسترود شده یک ساختمان هستند [ ۲۸ ]. داده‌های LoD1 مورد استفاده مربوط به سال‌های ۲۰۱۵ و ۲۰۱۸ هستند و به صورت رایگان قابل دسترسی هستند (آدرس: https://transparenz.hamburg.de/ ، در ۱۵ نوامبر ۲۰۲۱ قابل دسترسی است). به‌علاوه، عکس‌های ارتوبردی نقاط مختلف زمان از Google Earth (url: https://www.google.com/intl/de_de/earth/ )برای شناسایی تغییرات ساختمانی استفاده شد. این اطلاعات تغییر تعیین شده به صورت دستی به عنوان داده مرجع استفاده شد.
در آلمان، Zentrale Stelle Hauskoordinaten und Hausumringe (ZSHH) آژانس دولتی است که مسئول توزیع مختصات ساختمان و ردپا است. از سال ۲۰۱۵، سالانه مجموعه داده های LoD1 به روز شده را برای کل قلمرو فدرال منتشر می کند. در بیشتر موارد، ردپای ساختمان از نقشه کاداستر دیجیتال آلمان ( Amtliche Digitale Liegenschaftskarte ) اساس تولید این ساختمانهای LoD1 را تشکیل می‌دهد. دقت موقعیتی بالای ± ۱ متر این را مبنایی مناسب برای مطالعه ما می‌سازد. ساختمان ها با استفاده از اندازه گیری ارتفاع از یک اسکنر لیزری یا بررسی فتوگرامتری اکسترود شدند، که به موجب آن می توان دقت ارتفاع ± ۵ متر را انتظار داشت [ ۴۰ ].
در مورد ما، ما فقط از ردپاها استفاده می کنیم تا امکان انتقال به مجموعه داده های دوبعدی را فراهم کنیم. با این حال، ارزیابی اطلاعات ارتفاع در مرحله بعدی قابل تصور است، که تجزیه و تحلیل تغییرات کف را در مورد ردپاهای منطبق ممکن می کند. ارزیابی عملکرد ساختمان نیز قابل تصور است، اما از آنجایی که همیشه به آن اختصاص داده نمی شود، ما آن را در این تحلیل لحاظ نمی کنیم.
از آنجایی که ما مطالعه خود را بر تمایز بین اصلاح و جایگزینی ساختمان متمرکز کردیم، تنها چند ضلعی های ساختمانی از جفت شی غیر یکسان مورد بررسی قرار گرفت. ما روی تمایز بین جفت‌های ساختمان تغییر یافته (اصلاح یا جایگزین) و بدون تغییر تمرکز نکردیم. بنابراین، برای شناسایی جفت‌های شی غیر یکسان، یک رویکرد ساده‌شده را انتخاب کردیم. اگر نقاط پاره خط یک ساختمان بیشتر از ۱ متر از بخش های خط ساختمان مرتبط باشد، جفت ساختمان به عنوان غیرهمسان در نظر گرفته می شود. بنابراین، در موارد نادر، جفت‌های غیریکسان از اشیاء در واقع ساختمانهای بدون تغییر بودند که اصلاحات جزئی موقعیت برای آنها انجام شده بود. با این حال، از آنجایی که ما فقط می خواستیم بین ساختمان های جایگزین و اصلاح شده تمایز قائل شویم، این جفت ساختمان های اصلاح شده به عنوان اصلاح در نظر گرفته شدند.
مجموعه داده ۲۰۱۵ شامل ۷۲۶۷۵ شی و مجموعه داده ۲۰۱۸ ۷۷۳۰۱ شی بود. در مجموع ۲۲۸۵ جفت شی غیر یکسان در این مطالعه مورد بررسی قرار گرفت، که نشان دهنده انحراف موقعیت حداقل ۱± متر برای جفت شیء یکسان است. شکل ۲ منطقه مورد مطالعه را نشان می دهد، با جفت شی غیر یکسان بررسی شده با رنگ صورتی برجسته شده است. این جفت اشیاء یا ساختمان تخریب شده ای را نشان می دهند که با یک ساختمان جدید جایگزین شده است یا همان ساختمانی که به طور جزئی توسعه یافته / تخریب شده است (اصلاح یا در موارد نادر اصلاح موقعیت). برای هر جفت شی غیر یکسان، از تصاویر هوایی استفاده شد تا مشخص شود که آیا این یک ساختمان جایگزین شده یا تغییر یافته است که به عنوان مرجع عمل می کند.
۲٫۲٫ انواع تغییرات ساختمانی
در این تحقیق، هندسه برداری دو مجموعه داده دوبعدی (در اینجا ردپای LoD1) که نقاط مختلف زمان (T1، T2) را نشان می‌دهند، به منظور شناسایی تغییرات مورد تجزیه و تحلیل قرار گرفت.
انواع مختلف تغییرات ساختمان به طور مثال در جدول ۱ نشان داده شده است. برای اشیاء مرجع، تنها جایگزینی و اصلاح تعیین شد.
۲٫۳٫ رویه های تطبیق
در اینجا روش‌های تطبیق به طور خلاصه ارائه می‌شوند و تنها روشی که توسعه داده‌ایم با جزئیات شرح داده شده است.
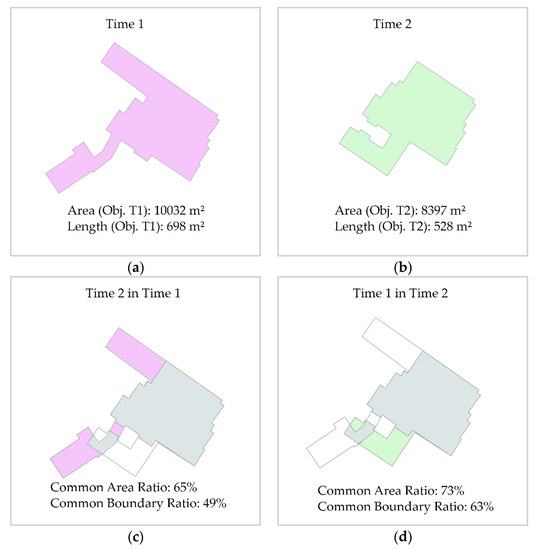
۲٫۳٫۱٫ نسبت مساحت مشترک ( CAR )
در مطالعات قبلی، جفت اشیایی که باید مورد بررسی قرار گیرند، اغلب در یک پیش فرآیند، بر اساس میزان همپوشانی، شناسایی می شدند تا در مراحل بعدی عمیق تر بررسی شوند [ ۳۴ ، ۳۵ ، ۴۱ ]. برای این منظور برای هر جفت شی نسبت همپوشانی مربوطه محاسبه می شود و مقدار پایین تر از این دو مقدار انتخاب می شود:
جایی که نواحی اشیاء در اولین مجموعه داده هستند و آن دومی تقاطع هر دو به صورت نشان داده می شود . در مورد m:n (بسیار تا زیاد) تغییرات، یا همچنین می تواند از مجموعه ای از نواحی چند شیء تشکیل شده باشد (< >). در این مورد، بررسی کردیم که آیا چند ضلعی های حل شده دارای درجه تطابق بالاتری هستند و سپس مقدار تطابق بهتر را انتخاب کردیم. محدوده مقادیر از ۰ تا ۱ است که ۰ مربوط به عدم تطابق (۰%) و ۱ به تطابق کامل (۱۰۰%) است. تابع حداکثر در اینجا توصیه نمی شود، زیرا مقدار ۱۰۰٪ فقط نشان می دهد که یک سطح در سطح دیگر قرار دارد.
۲٫۳٫۲٫ نسبت مرز مشترک ( CBR )
مشابه CAR ، درجه تطبیق خطوط چند ضلعی ( ) را می توان برای هر جفت شی ارزیابی کرد. در اینجا بخش ها در هر دو نقطه از زمان بررسی می شوند تا مشخص شود که آیا آنها در یک محدوده تحمل معین منطبق هستند یا خیر ( ). برای انجام این کار، بخش‌های اشیاء اولین نقطه زمانی با بخش‌های بافر قطع می‌شوند. ) از نقطه زمانی دوم و بالعکس. در مجموعه داده های قدیمی، ساختمان ها اغلب به اشتباه شامل گاراژها، زیرگذرهای دراز یا روگذر بودند، که منجر به نتایج تطبیق ضعیفی شد، حتی زمانی که منطقه همپوشانی همان ساختمان را توصیف می کرد. در مقایسه با CAR ، بهتر است یک تابع حداکثر تعیین شود، زیرا تابع حداکثر مقادیر بالاتری را در صورت تغییرات یا اصلاح داده ها ارائه می دهد:
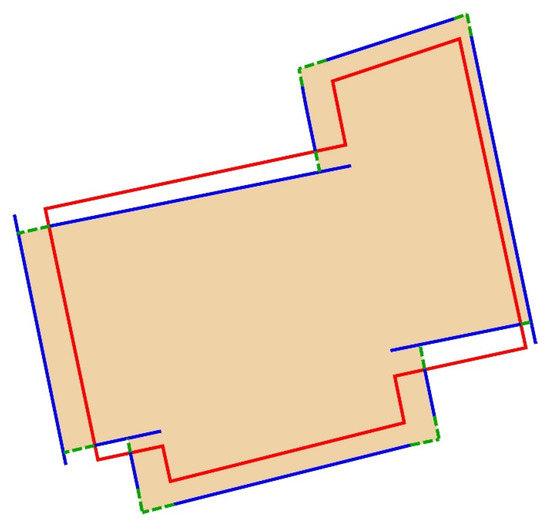
جایی که خطوط چند ضلعی در اولین مجموعه داده و آن دومی آن بخش‌های خطی از مجموعه داده اول که در بخش‌های بافر مجموعه داده دوم قرار دارند، به شرح زیر هستند و بالعکس. آنها بخش هایی را نشان می دهند که با یکدیگر مطابقت دارند. علاوه بر این، در مورد m:n تغییرات، یا می تواند شامل مجموعه ای از خطوط چند شیء (< >). در این مورد باید از قطعات چند ضلعی های حل شده استفاده شود. باز هم، محدوده مقادیر از ۰ تا ۱ است، که در آن ۰ مربوط به عدم تطابق (۰٪) و ۱ به یک جفت شی کاملا منطبق (۱۰۰٪) است. نمونه هایی از CAR و CBR در شکل ۳ نشان داده شده است.
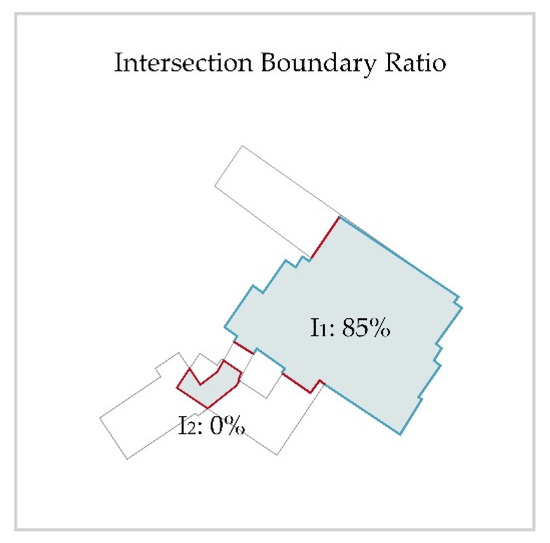
۲٫۳٫۳٫ نسبت مرز تقاطع ( IBR )
IBR مشابه CBR است با این تفاوت که مناطق تقاطع همپوشانی به صورت جداگانه ارزیابی می شوند. این دقت را بهبود می بخشد زیرا در برخی موارد تغییرات پیچیده تری رخ داده است. برای مثال، اشیاء ممکن است تا حدی در یک طرف تخریب شده باشند و از طرف دیگر گسترش یافته باشند ( شکل ۳ ). زمانی که این نواحی روی یکدیگر همپوشانی داشته باشند، وضعیت سخت‌تر می‌شود، زیرا در این صورت ناحیه تقاطع دارای یک بخش تغییر یافته و بدون تغییر است.
برای این منظور، ما تجزیه و تحلیل CBR را گسترش داده ایم تا مناطق تقاطع را به صورت جداگانه در نظر بگیریم. هر چند ضلعی تقاطع ( ) بررسی می شود تا مشخص شود کدام یک از بخش های آن ( ) با خطوط کلی هر دو شی اصلی مطابقت دارد ( و ). برای اینکه بتوان انحرافات موقعیت را در نظر گرفت، بافر نیز در اینجا به عنوان محدوده تحمل اعمال می شود ( ):
برخلاف CAR یا CBR (که هر دو یک جفت شی را به‌عنوان یک کل در نظر می‌گیرند)، IBR امکان تجزیه و تحلیل متفاوت‌تری از هر ناحیه تقاطع جداگانه یک جفت شی را فراهم می‌کند. مقدار IBR ۱ (۱۰۰%) است اگر تمام بخش های خط یک منطقه تقاطع در داخل بخش های بافر شی اصلی از هر دو نقطه زمانی قرار گیرند. مانند دو روش دیگر، اگر تغییرات m:n رخ دهد، مناطق متقاطع حل شده را می توان برای به دست آوردن مقادیر تطابق بهتر بررسی کرد.
شکل ۴ نه تنها نشان می دهد که مناطق تقاطع را می توان به صورت جداگانه تجزیه و تحلیل کرد، بلکه درصد همپوشانی می تواند به طور قابل توجهی بیشتر از CBR یا CAR باشد. لازم به ذکر است که نتایج IBR و CBR تنها زمانی متفاوت است که گسترش و ساختارشکنی با هم اتفاق بیفتند.
۲٫۳٫۴٫ فاصله هاسدورف ( HDD )
فاصله Hausdorff در بسیاری از کاربردها که تعداد نقاط در دو مجموعه داده شده استفاده می شود برابر نیست، و بنابراین هیچ مکاتبه ای داده نمی شود. برای هر جفت از اشیاء، چند ضلعی از اولین شی است و چند ضلعی از جسم دوم اشاره می کند به عنوان یک مجموعه داده شده در نظر گرفته می شوند. فاصله هاسدورف جهت‌دار بین A و B، مجموع این مجموعه‌های نقطه‌ای را توصیف می‌کند که بزرگترین فاصله بین نقاط A و نزدیک‌ترین نقطه B است:
حداکثر دو سوپرما ( ) فاصله هاسدورف است که حداقل در مفهوم ریاضی یک متریک است، زیرا قطعیت مثبت، تقارن و نابرابری مثلث را برآورده می کند (برای جزئیات بیشتر به [ ۳۹ ] مراجعه کنید):
حداقل مقدار ۰ متر است و حداکثر مقدار از حداکثر وسعت بزرگترین چند ضلعی ساختمان در مجموعه داده داده شده بیشتر نیست (حداقل در مورد جفت چند ضلعی های همپوشانی).
از آنجایی که در مورد ما می‌خواستیم بدانیم آیا جفت شی همان ساختمان را توصیف می‌کند، تابع حداقل را نیز بررسی کردیم. با این کار، ما می‌خواستیم بررسی کنیم که آیا می‌توان با ساختمانهای اصلاح‌شده به نتایج بهتری دست یافت (به عنوان مثال، در صورت حذف روگذرها):
واحد فاصله محاسبه شده چند ضلعی های زیرین است.
۲٫۳٫۵٫ چند ضلعی و بخش های خط ( PoLiS )
PoLiS هدایت شده میانگین فاصله هر نقطه از یک چند ضلعی A را توصیف می کند ( ) به رئوس (یا نقاط) یک چند ضلعی دیگر B ( ) در هر جفت شی (برای جزئیات بیشتر به [ ۱۴ ] مراجعه کنید):
مجموع وزنی دو پارامتر جهت دار ( ) برای به دست آوردن یک متریک متقارن و مشابه استفاده می شود:
جایی که و برای عادی سازی تعداد نابرابر توزیع شده نقاط اشیاء A و B برای به دست آوردن میانگین وزنی استفاده می شود. مانند HDD ، حداقل ۰ متر است، و حداکثر از عریض ترین ساختمان در مجموعه داده بزرگتر نیست. یکی از مزایای HDD و PoLiS این است که هیچ پارامتر اضافی مانند محدوده تحمل ( مانند CBR و IBR .
دوباره، می‌خواهیم بررسی کنیم که آیا مقدار پایین‌تر پارامترهای هدایت‌شده برای تمایز بهتر بین تغییرات و ساختارهای جایگزین مناسب‌تر است یا خیر:
مانند قبل، واحد همان چند ضلعی های زیرین است.
شکل ۵ نشان می دهد که یک مجموعه ساختمانی بزرگتر در طول زمان ساخته شده است، اگرچه بخش های کشیده (که با یک فلش مشخص شده اند) در واقعیت تغییر نکرده اند. با اعمال حداکثر تابع HDD یا مجموع وزنی PoLiS در این مثال، اشیاء درگیر فواصل بیشتری خواهند داشت، در حالی که استفاده از تابع حداقل منجر به فواصل کمتر می شود. به عنوان مثال، برای HDD ، مقدار ۱۵۳ متر برای شی علامت گذاری شده به دست می آید، در حالی که برای HDDmin تنها ۱۶ متر به دست می آید. با استفاده از تابع حداقل، زیرمناطق اصلاح شده چنین مقادیر بالایی را دریافت نمی کنند و می توانند بهتر از ساختمان های جایگزین متمایز شوند، به همین دلیل است که ما این پارامترهای تنظیم شده را نیز در نظر گرفتیم.
۲٫۴٫ تعیین آستانه و خطا
۲٫۴٫۱٫ آستانه بهینه
آستانه های بهینه برای هر روش تطبیق تعیین شد، که سپس برای تمایز بین ساختمان های اصلاح شده و جایگزین استفاده شد ( شکل ۶ ). این با یک رویکرد تکراری انجام شد. برای هر روش تطبیق، محدوده ای بر اساس مقادیر حداقل و حداکثر مربوطه تعیین شد. بر اساس ارجاعات داده شده از تغییرات ساختمان (n-اصلاح = ۱۳۵۹؛ n-جایگزین شده = ۹۲۶)، یک خطای کل برای هر مقدار آستانه ممکن در محدوده تعیین شده (تا یک رقم اعشار) تعیین شد و سپس مقدار آستانه با کمترین خطا انتخاب شد.
۲٫۴٫۲٫ کل خطا
خطای کل با مرتبط کردن نسبت مساحت ساختمانی که به طور نادرست تعیین شده به مساحت کل ساختمان ها تعیین شد:
۲٫۴٫۳٫ خطای کاربر
خطای کاربر با مرتبط کردن مساحت تغییرات تعیین شده توسط روش تطبیق به مساحت ساختمانهای نادرست تعیین شده تعیین شد:
۲٫۴٫۴٫ خطای سازنده
خطای تولیدکننده با مرتبط کردن ناحیه تغییرات مرجع به مساحت ساختمانهای نادرست تعیین شده تعیین شد:
۲٫۵٫ ایجاد انحرافات موقعیت
از آنجایی که داده های ورودی داده شده دارای دقت موقعیتی بالای ± ۱ متر هستند، انحراف موقعیت اضافی در مرحله بعدی اضافه شد. با این خطاهای شبیه‌سازی‌شده، باید قابلیت انتقال به مجموعه‌های داده با همسانی کمتر ممکن شود. ما همچنین بررسی کردیم که چگونه انحراف موقعیت بر دقت روش‌های تطبیق بررسی شده تأثیر می‌گذارد.
برای این منظور، قطعات چند ضلعی های ساختمان به صورت جانبی با افزایش ۰٫۲۵ متر تا ± ۵ متر جابه جا شدند. جابجایی تصادفی بود و از یک توزیع نرمال گاوسی پیروی می‌کرد، به همین دلیل است که ما این روش را «مولد خطای زنگ تصادفی» (RBEG) نامیدیم. هر چند ضلعی ساختمان به چند بخش تقسیم شد که به موجب آن تنها بخش هایی که جهت خود را حداقل ۲۰ درجه تغییر دادند از هم جدا شدند. پس از اینکه بخش ها به صورت جانبی با توجه به جهت کلی خود جابجا شدند، تا زمانی که با قطعه همسایه اصلی قطع شدند تا یک چندضلعی بسته را اصلاح کنند، گسترش یافتند. پس از آن، پوشش های حاصل حذف شدند.
شکل ۷ فرآیند را به صورت شماتیک بر روی ردپای ساختمان نشان می دهد. شکل ۸ ، از سوی دیگر، نمونه ای از مجموعه داده تولید شده را نشان می دهد. لازم به ذکر است که مقدار تصادفی به طور معمول توزیع می شود، به طوری که اگرچه نادر است، اما می توان از مقادیر جابجایی مورد انتظار به طور قابل توجهی فراتر رفت.
این فرآیند ده بار برای هر عرض (۰٫۲۵ متر، ۰٫۵ متر، …، ۴٫۷۵ متر و ۵ متر) به دلیل تولید مقدار تصادفی تکرار شد. پس از آن، یک مقدار آستانه بهینه از ده مجموعه داده هر عرض تعیین شد، که به نوبه خود برای تشکیل یک مقدار آستانه متوسط در هر عرض استفاده شد.
این روش برای همه روش‌های تطبیق بررسی شده اعمال شد، که از طریق آن می‌توان تعیین کرد که تا چه اندازه عدم دقت موقعیت بر نتایج تطبیق تأثیر می‌گذارد. برای روش های تطبیق CBR و IBR ، محدوده تحمل بافر ( ) با توجه به افزایش انحراف افزایش یافتند.
۳٫ نتایج
ما مطالعات مربوط به CAR ، CBR ، PoLiS و HDD را برای مقایسه جفت اشیاء مربوط به یک ساختمان جایگزین یا اصلاح شده بررسی کردیم. این بخش ابتدا توزیع‌های تعیین‌شده جایگزین‌ها و تغییراتی را که از رویه‌های تطبیق فردی حاصل می‌شود، ارائه می‌کند. علاوه بر این، مقادیر آستانه بهینه مربوطه و دقت به دست آمده با آنها ارائه شده است. در نهایت، نشان داده شده است که تا چه اندازه انحراف موقعیت بر دقت روش های تطبیق بررسی شده تأثیر می گذارد.
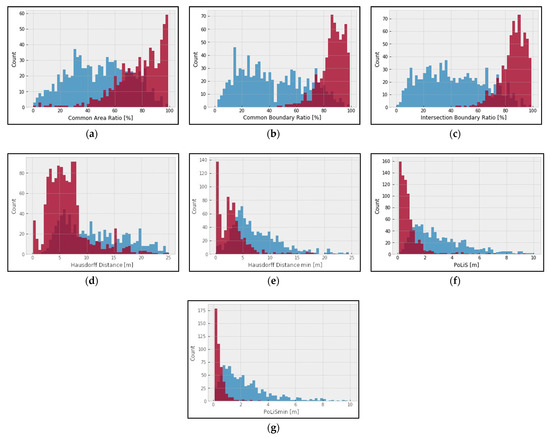
۳٫۱٫ توزیع ها
در مجموع ۲۲۸۵ جفت شی غیر یکسان در مجموعه داده مرجع گنجانده شد که از این تعداد ۱۳۵۹ ساختمان اصلاح شده و ۹۲۶ جفت ساختمان جایگزین شدند. برای این جفت‌های شی، مقادیر برای تمام روش‌های تطبیق بررسی‌شده، که توزیع آنها سپس به صورت گرافیکی در قالب هیستوگرام نشان داده شد، محاسبه شد ( شکل ۹ ).
در این هیستوگرام‌ها مشاهده می‌شود که برای CAR ، IBR و CBR ، ساختمانهای اصلاح‌شده اغلب مقادیر بالاتری را به دست می‌آورند و مقادیر پایین‌تر بیشتر نشان‌دهنده ساختمانهای جایگزین است. HDD ( min ) و PoLiS ( min )، از سوی دیگر، تصویر مخالف را نشان می‌دهند، با مقادیر کمتر نشان‌دهنده یک ساختمان اصلاح‌شده، و ساختمانهای جایگزین با افزایش مقادیر بیشتر انتظار می‌رود. علاوه بر این، می توان دید که CAR و هر دو HDDانواع دارای همپوشانی نسبتاً بالاتری از تغییرات و جایگزینی ساختمان هستند که به صورت نوارهای قرمز تیره نشان داده شده است. قابل توجه است که تابع حداقل در مقایسه انواع HDD به طور قابل توجهی بهتر عمل می کند ، در حالی که دو نوع PoLiS توزیع مشابهی را نشان می دهند.
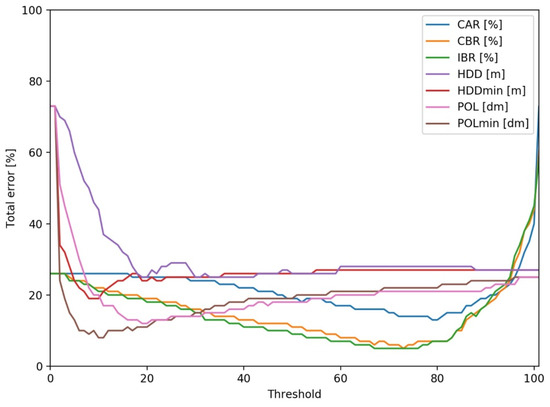
۳٫۲٫ آستانه ها و دقت های بهینه
بر اساس مقادیر محاسبه شده، آستانه های بهینه برای هر روش تطبیق، همانطور که در بخش ۲٫۴ توضیح داده شد، تعیین شد .
اگر تمام تغییرات ساختمان ۲۲۸۵ به عنوان اصلاح تعیین شود، کل خطا ۲۷٪ خواهد بود. در مقابل، اگر تمام تغییرات به عنوان ساختمان های جایگزین تعیین شود، کل خطا ۷۳٪ خواهد بود. این برای همه روش های تطبیق سازگار است. در شکل ۱۰ ، این افراط‌ها برای روش‌های تطبیق با درصد تطابق ( CAR ، CBR و IBR ) و با نرخ‌های فاصله ( HDD ، HDDmin ، PoLiS و PoLiSmin ) معکوس شده‌اند، زیرا نرخ تطابق بالا با فواصل کم قابل مقایسه است.
نتایج دقیق در جدول ۲ نشان داده شده است که مقادیر آستانه و همچنین دقت های حاصل را نشان می دهد. علاوه بر خطای کل ، دقت نیز بر اساس دو کلاس مورد بررسی (ساختمان جایگزین یا اصلاح شده) تقسیم شد. بین مساحتی که در داده های مرجع به اشتباه تعیین شده است ( خطای تولید ) در مقابل ناحیه ای که با روش های تطبیق نادرست تعیین شده است ( خطای کاربر ) تمایز قائل شد. به عنوان مثال، برای PoLiSmin ، خطای کل۸٫۳ درصد است که ۱۷٫۷ درصد از مناطق مرجع به اشتباه به عنوان ساختمان های جایگزین شناسایی شده اند و ۶٫۳ درصد از ساختمان های شناسایی شده نادرست هستند. این بدان معناست که تقریباً هر ششمین ساختمان تعویض شده به این صورت تشخیص داده نشده است و از بین ساختمان هایی که تعیین شده تعویض شده اند، از هر ۱۶ ساختمان حدود یک ساختمان نادرست بوده است.
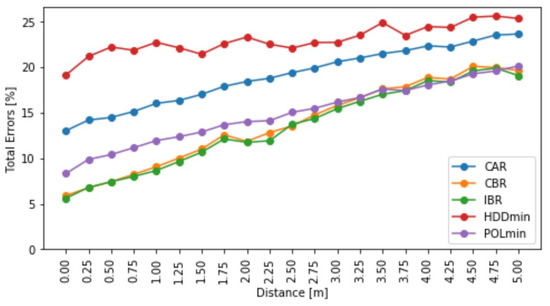
۳٫۳٫ آستانه و دقت انحرافات ایجاد شده
انحراف موقعیت ایجاد شده با RBEG همانطور که در بخش ۲٫۵ توضیح داده شد با روش های مختلف تطبیق مورد بررسی قرار گرفت. از آنجایی که حداقل عملکردهای PoLiS و HDD ( PoLiSmin و HDDmin ) نتایج بهتری ارائه می‌دهند، در این آزمون فقط از اینها استفاده شد. بر اساس انحرافات ایجاد شده، آستانه های بهینه مطابق جدول ۳ تعیین شد .
با استفاده از مقادیر آستانه بهینه در جدول ۳ ، کل خطاها برای روش های تطبیق بررسی شده تعیین شد. شکل ۱۱ نشان می دهد که برای تمام روش های تطبیق، خطای کل با افزایش انحراف موقعیت افزایش می یابد. در انحراف موقعیت ۱٫۷۵ متر یا بالاتر، مزایای کوچک CBR و IBR به تدریج کاهش یافت به طوری که آنها با PoLiSmin همگرا شدند . با این حال، افست بین CAR و PoLiSmin با افزایش انحراف ثابت باقی ماند. خطای کل HDDmin _با افزایش انحراف نسبتاً کمتر افزایش یافت، اما به طور کلی دقت کمتری را نشان داد.
۴٫ بحث
نتایج در بخش ۳٫۲ نشان داده است که برای منطقه مورد مطالعه، که شامل ردپاهایی با دقت موقعیتی بالای ۱ ± متر است، CBR و IBR دقیق ترین روش های تطبیق برای تمایز بین ساختمان های اصلاح شده و جایگزین شده هستند. خطای کل CBR و IBR به ترتیب ۵٫۹% و ۵٫۶% با آستانه بهینه ۷۲% و ۷۴% است . با توجه به سوال اول تحقیق (RQ1)، این آستانه ها کمی بالاتر از انتظارات هستند، اما این احتمالاً به دلیل دقت منبع داده است. با این حال، این آستانه ها با فرض روتزینگر که محدوده ای را تا ۷۰ درصد برای اکثر برنامه ها تخمین زده است، فاصله زیادی ندارند [ ۳۸ ].]. در مقایسه با CBR ، IBR تنها زمانی نتایج بهتری را ارائه می دهد که تخریب و گسترش ساختمان به طور همزمان در یک اصلاح اتفاق می افتد. از آنجایی که این مورد در منطقه مورد مطالعه به ندرت اتفاق می افتد، تفاوت کلی IBR با CBR حداقل است. معیار PoLiS دارای خطای کل ۱۲٫۷٪ است که تقریباً دو برابر بزرگتر است. کل خطای CAR تقریباً یکسان است (۱۳٫۰%). در مقابل، HDD برای تمایز کمتر مناسب است، زیرا کل خطای آن بسیار زیاد است (۲۵٫۳٪). Avbelj همچنین دریافت که HDD به انحرافات بسیار حساس تر از PoLiS است[ ۱۴ ] که با یافته های ما مطابقت دارد.
علاوه بر این، در بخش ۳٫۲ نشان داده شد که برای تشخیص اصلاح از جایگزینی، حداقل توابع PoLiS و HDD ( PoLiSmin و HDDmin ) از حداکثر توابع دقیق‌تر هستند، بنابراین به سؤال تحقیق دوم (RQ2) پاسخ می‌دهند. PoLiSmin دارای خطای کل ۸٫۳٪ است که تفاوت زیادی با CBR و IBR ندارد. از طرف دیگر، HDDmin دارای خطای کل ۱۹٫۱٪ است که کاملاً نادرست است.
برای پرداختن به سوال سوم تحقیق در مورد اینکه چگونه انحرافات موقعیت بر دقت تاثیر می گذارد (RQ3)، ما انحرافات موقعیت تصادفی را ایجاد کردیم. در بخش ۳٫۳ . ما نشان داده ایم که PoLiSmin از انحراف ۱٫۷۵ متر و بیشتر به دقت CBR و IBR همگرا می شود. این فرضیه ما را در سوال تحقیق ۳ تایید کرد که با افزایش انحراف موقعیت، CBR و IBR به دلیل دامنه های تحمل کمتر برای تمایز مناسب هستند. در انحراف ۲٫۷۵ متر، CBR ، IBR و PoLiS به خطای کل ۱۵٪ می رسند که دقت کافی در نظر گرفته نمی شود. بدین وسیله، برایCAR ، یک مقدار آستانه در محدوده ۷۸٫۶٪ تا ۴۶٫۸٪ با افزایش انحراف به دست آمد، که مشابه مشاهده Rutzinger از ۷۰٪ تا ۵۰٪ است [ ۳۸ ]. از سوی دیگر، برای CBR و IBR ، مقدار آستانه با افزایش انحراف افزایش یافت، به طوری که مقادیر آستانه برای داده های اصلی (بدون انحراف اضافی) به ترتیب ۷۲٪ و ۷۴٪ بود، در حالی که برای انحراف بالاتر (۵± متر) بود. اینها حدود ۸۱ درصد و ۷۸ درصد بودند. با این حال، دامنه این آستانه ها در مقایسه با CAR بسیار کوچکتر است. برای PoLiSmin، آستانه های تعیین شده بسیار شبیه به انحراف موقعیت هستند (با توجه به انحراف استاندارد ± ۱ متر به اضافه انحراف ایجاد شده اضافی)، که زمانی که انحراف استاندارد شناخته شده باشد یک مزیت است.
به طور کلی می توان گفت که CBR و IBR روش های دقیق تری برای تمایز بین ساختمان های اصلاح شده و جایگزین شده برای انحراف موقعیت تا ۱٫۷۵ متر هستند. از آنجایی که CBR به حدود نیمی از زمان محاسبه IBR نیاز دارد، ترجیح داده می شود. مزیت قابل توجه PoLiSmin و HDDmin این است که هیچ پارامتر اضافی مانند تحمل بافر ( ) مانند CBR و IBR مورد نیاز است. اگر منابع داده های مختلف با دقت موقعیت متفاوت یا ناشناخته مقایسه شوند، PoLiSmin نیز توصیه می شود. علاوه بر این، PoLiSmin به نیمی از زمان محاسبه CBR (و یک چهارم زمان IBR ) نیاز دارد که برای مجموعه داده‌های بزرگتر سودمند است. از طرف دیگر، CAR و HDD به دلیل سطح بالای عدم دقت حتی با انحرافات موقعیت کوچک توصیه نمی شوند.
برای شناسایی ساختمان های بدون تغییر (یکسان)، متریک PoLiS تنظیم نشده مفیدتر از PoLiSmin است. آستانه هایی که در آن ساختمان را می توان بدون تغییر در نظر گرفت باید در مطالعه دیگری تعیین شود.
۵٫ نتیجه گیری ها
در این مقاله ما بررسی کرده‌ایم که چگونه می‌توان تغییرات ساختمانی را از ساختمانهای جایگزین براساس هندسه‌های برداری متمایز کرد. برای این منظور، ما ۲۲۸۵ جفت ساختمان را بر اساس تغییرات مجموعه داده در یک منطقه مطالعه بزرگ در هامبورگ بررسی کردیم.
ما به‌صورت دستی از طریق تصاویر هوایی تعیین کردیم که آیا جفت‌های ساختمان غیریکسان، ساختمانهای تغییر یافته (اصلاح شده) یا تخریب شده و ساختمانهای جدید ساخته شده (ساختمانهای جایگزین) هستند که به عنوان مرجع عمل می‌کنند. با استفاده از این داده‌های مرجع، روش‌های مختلف تطبیق را بررسی کردیم و دقت آنها و همچنین آستانه‌های بهینه برای تمایز بین ساختمانهای اصلاح‌شده و جایگزین را تعیین کردیم.
ما دریافتیم که روش‌های تطبیق نسبت مساحت مشترک ( CAR )، فاصله هاوسدورف ( HDD ) و بخش‌های خط نقطه ( PoLiS ) برای تمایز بین اصلاح و جایگزینی کمتر مناسب هستند، زیرا جفت‌های ساختمان دارای تغییرات بسیار زیادی هستند ( کل خطا : ۱۳٫۰٪ به ترتیب ۲۵٫۳ و ۱۲٫۷ درصد). در مقابل، روش‌های تطبیق مبتنی بر خط از مرز مشترک ( CBR ) و نسبت مرز تقاطع ( IBR )، که ما توسعه دادیم، توانستند نتایج بسیار دقیق‌تری تولید کنند (به ترتیب خطای کل : ۵٫۹٪ و ۵٫۶٪).
HDD و PoLiS به تغییرات بسیار حساس هستند، و همانطور که جفت‌های غیریکسان ساختمانها را بررسی کردیم، این روشها را برای تعیین اینکه آیا یک تابع حداقل برای تمایز مناسب‌تر است یا خیر، آزمایش کردیم. برای PoLiSmin ، نتایج بهتری به دست آمد ( خطای کل : ۸٫۳%)، که برای HDDmin صدق نمی کند ( کل خطا : ۱۹٫۱%).
از آنجایی که مجموعه داده زیربنایی بسیار دقیق بود، ما همچنین بررسی کردیم که چقدر انحراف موقعیت بر دقت تأثیر می گذارد، که باید امکان انتقال به مجموعه داده های کمتر مطابقت را بدهد. برای پرداختن به این سوال، یک روش جدید برای ایجاد انحرافات موقعیت ایجاد کردیم. علاوه بر این، مقادیر آستانه تعیین شده در این آزمون می تواند به عنوان مبنایی برای بررسی های دیگر مورد استفاده قرار گیرد. ما به تدریج بخش های خط را به سمت جانبی در محدوده ۰ تا ۵ متر جابجا کردیم، با جابجایی موقعیت به دنبال توزیع نرمال گاوسی. این نشان داد که تا موقعیت افست ۱٫۷۵ متر، CBR و IBR بهترین دقت را دارند. با این حال، حداقل تابع PoLiSقابل مقایسه است و از ارتفاع ۷۵/۲ متری و بالاتر به همان دقت دو روش ذکر شده قبلی دست می یابد. با این حال، برای انحرافات موقعیت بزرگتر، روش ها دارای خطای کل بیش از ۱۵٪ هستند و بنابراین به طور فزاینده ای نادرست هستند.
منابع
- بیلجکی، اف. استوتر، جی. لدوکس، اچ. زلاتانوا، اس. Çöltekin، A. کاربردهای مدل های سه بعدی شهر: بررسی وضعیت هنر. ISPRS Int. J. Geo-Inf. ۲۰۱۵ ، ۴ ، ۲۸۴۲-۲۸۸۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ایوانز، اس. لیدیارد، آر. Steadman، P. 3DStock: نوع جدیدی از مدل سه بعدی ساختمان سهام انگلستان و ولز، برای استفاده در تجزیه و تحلیل انرژی. محیط زیست طرح. ب مقعد شهری. علوم شهر ۲۰۱۷ ، ۴۴ ، ۲۲۷-۲۵۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Vanderhaegen، S. Canters، F. نقشه برداری شکل شهری و عملکرد در سطح بلوک شهر با استفاده از متریک های فضایی. Landsc. طرح شهری. ۲۰۱۷ ، ۱۶۷ ، ۳۹۹-۴۰۹٫ [ Google Scholar ] [ CrossRef ]
- بیلجکی، اف. اوهوری، کالیفرنیا؛ لدوکس، اچ. پیترز، آر. Stoter, J. برآورد جمعیت با استفاده از مدل شهر سه بعدی: یک مطالعه چند مقیاسی در سطح کشور در هلند. PLoS ONE ۲۰۱۶ , ۱۱ , e0156808. [ Google Scholar ] [ CrossRef ]
- برویتمن، دی. کومن، ای. جاذبه هسته های شهری: متراکم شدن در مراکز شهر هلند. مطالعه شهری. ۲۰۲۰ ، ۵۷ ، ۱۹۲۰-۱۹۳۹٫ [ Google Scholar ] [ CrossRef ]
- هچت، ر. هرولد، اچ. بهنیش، م. Jehling، M. نقشه برداری از پویایی بلندمدت جمعیت و مسکن بر اساس تجزیه و تحلیل چند زمانی مورفولوژی های شهری. ISPRS Int. J. Geo-Inf. ۲۰۱۹ ، ۸ ، ۲٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- خانال، ن. اودین، ک. متین، MA; Tenneson، K. تشخیص خودکار الگوهای گسترش شهری فضایی و زمانی با ترکیب داده های OSM و Landsat در کاتماندو. Remote Sens. ۲۰۱۹ , ۱۱ , ۲۲۹۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- غمیسی، پ. راستی، ب. یوکویا، ن. وانگ، کیو. هوفل، بی. بروزون، ال. بوولو، اف. چی، م. اندرس، ک. گلوگوئن، آر. و همکاران ترکیب داده‌های چندمنبعی و چندزمانی در سنجش از راه دور: مروری جامع بر وضعیت هنر. IEEE Geosci. سنسور از راه دور Mag. ۲۰۱۹ ، ۷ ، ۶-۳۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- دای، سی. ژانگ، ز. Lin, D. یک روش دو جهته مبتنی بر شی برای استخراج ساختمان یکپارچه و تشخیص تغییر بین ابرهای نقطه چندوجهی. Remote Sens. ۲۰۲۰ , ۱۲ , ۱۶۸۰٫ [ Google Scholar ] [ CrossRef ]
- سستر، ام. Brenner, C. Datenquellen Und Methoden Für Eine Automatische Bestimmung von Gebäude- Und Siedlungsvolumen ; موسسه کارتوگرافی و ژئوانفورماتیک – دانشگاه لایبنیتس هانوفر: هانوفر، آلمان، ۲۰۰۲٫ [ Google Scholar ]
- ماتیکاینن، ال. Hyyppä، J.; آهوکاس، ای. مارکلین، ال. کارتینن، اچ. تشخیص خودکار ساختمان ها و تغییرات در ساختمان ها برای به روز رسانی نقشه ها. Remote Sens. ۲۰۱۰ , ۲ , ۱۲۱۷-۱۲۴۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- جباری، س. Zhang, Y. تشخیص تغییر ساختمان با استفاده از چند سنسور و تصاویر با زاویه دید چندگانه. IOP Conf. سر. محیط زمین. علمی ۲۰۱۶ , ۳۴ , ۰۱۲۰۱۸٫ [ Google Scholar ] [ CrossRef ]
- Gergelova، MB; لبانت، اس. کوزوویچ، اس. کوزوویکووا، ز. Pavolova، H. شناسایی سطوح سقف از نقاط ابری LiDAR توسط ابزار GIS: مطالعه موردی Lučenec، اسلواکی. پایداری ۲۰۲۰ ، ۱۲ ، ۶۸۴۷٫ [ Google Scholar ] [ CrossRef ]
- آوبلج، ج. مولر، آر. Bamler, R. A Metric for Polygon Comparison and Building Extraction Evaluation. IEEE Geosci. سنسور از راه دور Lett. ۲۰۱۵ ، ۱۲ ، ۱۷۰-۱۷۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- فو، ز. فن، ال. یو، ز. ژو، ک. اندازه‌گیری تشابه شکل مبتنی بر لحظه برای موجودیت‌های مساحتی در داده‌های برداری جغرافیایی. ISPRS Int. J. Geo-Inf. ۲۰۱۸ ، ۷ ، ۲۰۸٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- روتنشتاینر، اف. سون، جی. گرکه، ام. Wegner، JD; Breitkopf، U. Jung, J. نتایج معیار ISPRS در تشخیص اشیاء شهری و بازسازی ساختمان سه بعدی. ISPRS J. Photogramm. Remote Sens. ۲۰۱۴ ، ۹۳ ، ۲۵۶-۲۷۱٫ [ Google Scholar ] [ CrossRef ]
- وو، جی. وان، ی. چیانگ، ی. فو، ز. دنگ، ام. الگوریتم تطبیقی بر اساس نمودار ورونوی برای مناطق مسکونی چند ضلعی چند مقیاسی. دسترسی IEEE ۲۰۱۸ ، ۶ ، ۴۹۰۴–۴۹۱۵٫ [ Google Scholar ] [ CrossRef ]
- یانگ، م. آی، تی. یان، ایکس. چن، ی. Zhang، X. یک روش مبتنی بر نقشه-جبر برای تشخیص تغییر خودکار و به روز رسانی داده های مکانی در مقیاس های چندگانه. ترانس. GIS ۲۰۱۸ ، ۲۲ ، ۴۳۵-۴۵۴٫ [ Google Scholar ] [ CrossRef ]
- ژانگ، ی. هوانگ، جی. دنگ، م. چن، سی. ژو، اف. زی، اس. Fang, X. تطبیق خودکار داده‌های ساختمان چند مقیاسی بر اساس برچسب‌گذاری آرامش و ترکیب‌های الگو. ISPRS Int. J. Geo-Inf. ۲۰۱۹ ، ۸ ، ۳۸٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Carleer، AP; Wolff, E. تشخیص تغییر برای به‌روزرسانی‌های پایگاه داده برداری از طریق طبقه‌بندی منطقه‌ای داده‌های ماهواره‌ای VHR. در سنجش از دور برای پایش محیطی، کاربردهای GIS و زمین‌شناسی VII . انجمن بین المللی اپتیک و فوتونیک: بلینگهام، WA، ایالات متحده آمریکا، ۲۰۰۷; جلد ۶۷۴۹٫ [ Google Scholar ]
- Qin, R. تشخیص تغییر در مدل‌های ساختمان LOD 2 با تصاویر استریوی فضایی با وضوح بسیار بالا. ISPRS J. Photogramm. Remote Sens. ۲۰۱۴ ، ۹۶ ، ۱۷۹-۱۹۲٫ [ Google Scholar ] [ CrossRef ]
- آبدستار، م. Zhong، Y. تشخیص تغییر ساختمان ها بر اساس تطبیق شکل برای تصاویر سنجش از راه دور با وضوح چندگانه. ISPRS Int. قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی ۲۰۱۷ ، XLII-2/W7 ، ۶۸۳–۶۸۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هارتمن، ا. ماینل، جی. بهنیش، م. Hecht, R. Gebäudebestandsmonitoring—Prozessierungsschritte für den Aufbau homogeneer Gebäudedatensätze. Flächensparen Ökosystemleistungen Handl. ۲۰۱۶ ، ۶۹ ، ۲۰۳-۲۱۴٫ [ Google Scholar ]
- ماینل، جی. Krüger، T. Methodik eines Flächennutzungsmonitorings auf Grundlage des ATKIS-Basis-DLM. جی. کارتوگر. Geogr. Inf. ۲۰۱۴ ، ۶۴ ، ۳۲۴-۳۳۱٫ [ Google Scholar ] [ CrossRef ]
- منطقه اقتصادی اروپا گسترش شهری در اروپا – گزارش مشترک EEA-FOEN – آژانس محیط زیست اروپا ; دفتر انتشارات اتحادیه اروپا: لوکزامبورگ، ۲۰۱۶; در دسترس آنلاین: https://data.europa.eu/doi/10.2800/143470 (در ۱ دسامبر ۲۰۲۱ قابل دسترسی است).
- DESTATIS. Qualitätsbericht—Flächenerhebung Nach Art der Tatsächlichen Nutzung ; Statistisches Bundesamt (Destatis): ویسبادن، آلمان، ۲۰۱۸٫ [ Google Scholar ]
- Deutsche Bundesregierung. Die Deutsche Nachhaltigkeitsstrategie—Aktualisierung 2018 ; Presse-und Informationsamt der Bundesregierung: برلین، آلمان، ۲۰۱۸٫ [ Google Scholar ]
- بیلجکی، اف. لدوکس، اچ. Stoter, J. یک مشخصات LOD بهبود یافته برای مدل های ساختمانی سه بعدی. محاسبه کنید. محیط زیست سیستم شهری ۲۰۱۶ ، ۵۹ ، ۲۵-۳۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کادن، آر. کلبه، TH برآورد کل تقاضای انرژی کل شهر در ساختمانها با استفاده از مدل‌های معنایی شهر سه بعدی و داده‌های آماری. در مجموعه مقالات ISPRS Annals of the Photogrammetry، سنجش از دور و علوم اطلاعات فضایی، استانبول، ترکیه، ۲۷-۲۹ نوامبر ۲۰۱۳٫ جلد II-2-W1، صص ۱۶۳-۱۷۱٫ [ Google Scholar ]
- ژانگ، ایکس. استوتر، جی. آی، تی. کراک، ام.-جی. مولنار، ام. ارزیابی خودکار ترازهای ساختمان در نقشه های تعمیم یافته. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۳ ، ۲۷ ، ۱۵۵۰-۱۵۷۱٫ [ Google Scholar ] [ CrossRef ]
- بروولی، MA; Zamboni, G. روشی جدید برای ارزیابی دقت فضایی و کامل بودن ردپای ساختمان OpenStreetMap. ISPRS Int. J. Geo-Inf. ۲۰۱۸ ، ۷ ، ۲۸۹٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- کوین، آر. تیان، جی. Reinartz, P. تشخیص تغییر سه بعدی-رویکردها و کاربردها. ISPRS J. Photogramm. Remote Sens. ۲۰۱۶ ، ۱۲۲ ، ۴۱-۵۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- فن، اچ. Zipf، A.; فو، س. Neis، P. ارزیابی کیفیت برای ایجاد داده‌های ردپایی در OpenStreetMap. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۴ ، ۲۸ ، ۷۰۰-۷۱۹٫ [ Google Scholar ] [ CrossRef ]
- پدرینیس، اف. مورل، ام. Gesquière, G. Change Detection of Cities. در علوم زمین اطلاعات سه بعدی ; یادداشت های سخنرانی در اطلاعات جغرافیایی و نقشه برداری. Springer: Cham, Switzerland, 2015. [ Google Scholar ] [ CrossRef ]
- ژو، ایکس. چن، ز. ژانگ، ایکس. Ai, T. تشخیص تغییر برای ردپای ساختمان با سطوح مختلف جزئیات با استفاده از ترکیب شکل و تجزیه و تحلیل الگو. ISPRS Int. J. Geo-Inf. ۲۰۱۸ ، ۷ ، ۴۰۶٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- شوونگرت، RA سنجش از دور: مدل‌ها و روشها برای پردازش تصویر . مطبوعات دانشگاهی: کمبریج، MA، ایالات متحده آمریکا، ۲۰۰۶; شابک ۹۷۸-۰-۰۸-۰۴۸۰۵۸-۹٫ [ Google Scholar ]
- غنی، ارتش ملی; Abidin, SZZ طبقه بندی الگوی رشد شهری با استفاده از الگوریتم طول مرزی رابطه توپولوژیکی: یک مطالعه تجربی. در روندهای اخیر در فناوری اطلاعات و ارتباطات ; Saeed, F., Gazem, N., Patnaik, S., Saed Balaid, AS, Mohammed, F., Eds.; انتشارات بین المللی اسپرینگر: چم، سوئیس، ۲۰۱۸; صص ۵۴۵-۵۵۳٫ [ Google Scholar ]
- روتزینگر، ام. روتنشتاینر، اف. Pfeifer, N. مقایسه تکنیک‌های ارزیابی برای استخراج ساختمان از اسکن لیزری هوابرد. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. ۲۰۰۹ ، ۲ ، ۱۱-۲۰٫ [ Google Scholar ] [ CrossRef ]
- Veltkamp، R. تطبیق شکل: معیارها و الگوریتم‌های تشابه. در مجموعه مقالات کنفرانس بین المللی مدل سازی شکل و کاربردها، جنوا، ایتالیا، ۷-۱۱ مه ۲۰۰۱٫ ص ۱۸۸-۱۹۷٫ [ Google Scholar ]
- AdV. Produktstandard für 3D-Gebäudemodelle نسخه ۱٫۴ ; Arbeitsgemeinschaft der Vermessungsverwaltungen der Länder der Bundesrepublik Deutschland (AdV): مونیخ، آلمان، ۲۰۱۷؛ پ. ۶٫ [ Google Scholar ]
- کای، ال. شی، دبلیو. میائو، ز. هائو، ام. اقدامات ارزیابی دقت برای استخراج شی از تصاویر سنجش از دور. Remote Sens. ۲۰۱۸ , ۱۰ , ۳۰۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شکل ۱٫ روش شناسی این مطالعه.
شکل ۲٫ منطقه مورد مطالعه، شهر هامبورگ (۲۰۱۵-۲۰۱۸); چند ضلعی های تقاطع جفت شی غیر یکسان (n = 2285) را بررسی کرد که در سمت چپ به رنگ صورتی برجسته شده بودند.
شکل ۳٫ نمونه هایی از نسبت مساحت مشترک ( CAR ) و نسبت مرز مشترک ( CBR ) برای دو ردپای از نقاط زمانی مختلف: ( الف ) ساختمان در زمان ۱٫ ( ب ) ساختمان در زمان ۲٫ ( ج ) CAR و CBR از T1، T2. ( د ) CAR و CBR T2, T1. بنفش ناحیه قدیمی، سبز ناحیه جدید و خاکستری ناحیه همپوشانی است.
شکل ۴٫ نمونه ای از نسبت مرز تقاطع ( IBR ) که به طور جداگانه برای هر ناحیه از تقاطع I ۱ و I ۲ محاسبه می شود (همان اشیاء ورودی T1 و T2 مانند شکل ۳ ). خطوط آبی تطابق بخش‌های خط از T1 و T2 را نشان می‌دهند، خطوط قرمز بین T1 و T2 مطابقت ندارند و خاکستری ناحیه همپوشانی است.
شکل ۵٫ مثالی از فاصله هاسدورف ( HDD ) و تابع حداقل فاصله هاسدورف ( HDDmin ) برای یک مجتمع ساختمانی بزرگ و در حال تغییر که در آن مناطق تقاطع در واقعیت تغییر نکرده اند: ( الف ) ساختمان ها در زمان ۱٫ ( ب ) ساختمانها در زمان ۲٫ ( ج ) ساختمانهای زمان ۱ و زمان ۲ روی هم قرار گرفته اند.
شکل ۶٫ نمونه های شماتیک یک ساختمان اصلاح شده و یک ساختمان جایگزین شده: ( الف ) ساختمان اصلاح شده با سطح تقاطع بدون تغییر. ( ب ) ساختمان با تغییر منطقه تقاطع جایگزین شده است.
شکل ۷٫ مثال شماتیک خطاهای ایجاد شده: خطوط قرمز چند ضلعی اصلی، خطوط آبی قسمت های جدا شده و اخیراً جابجا شده، خطوط نقطه چین سبز خطوط توسعه یافته و چند ضلعی بژ چند ضلعی تازه تشکیل شده هستند.
شکل ۸٫ نمونه ای از انحرافات موقعیت ایجاد شده، که به موجب آن مراحل تکرار (۰٫۲۵ متر، ۰٫۵ متر، …، ۴٫۷۵ متر و ۵ متر) روی هم قرار می گیرند. خطوط قرمز چند ضلعی های اصلی را نشان می دهد.
شکل ۹٫ هیستوگرام روش‌های تطبیق بررسی شده: نوارهای آبی ساختمانهای اصلاح‌شده را نشان می‌دهند، نوارهای قرمز جایگزین ساختمانها هستند، و نوارهای قرمز تیره روی نوارهای آبی و قرمز قرار دارند. ( الف ) نسبت مساحت مشترک ( CAR )؛ ( ب ) نسبت مرز مشترک ( CBR )؛ ( ج ) نسبت مرز تقاطع ( IBR )؛ ( د ) فاصله Hausdorff; ( ه ) تابع حداقل فاصله هاسدورف ( HDDmin )؛ ( f ) چند ضلعی و بخش های خط ( PoLiS ). ( g ) حداقل عملکرد PoLiS ( PoLiSmin ).
شکل ۱۰٫ بررسی اجمالی تعیین مقادیر آستانه بهینه همه روش های تطبیق. برای مقایسه بهتر، مقادیر PoLiS (POL) و PoLiSmin (POLmin) به صورت دسی متر نشان داده می شوند.
شکل ۱۱٫ مجموع خطاها به ازای فاصله انحراف موقعیت ایجاد شده برای تشخیص ساختمان های اصلاح شده از جایگزین شده.
بدون دیدگاه