کلید واژه ها:
پیش بینی تقاضا ; وابستگی های مکانی-زمانی ؛ گراف شبکه های عصبی ; مکانیسم توجه
۱٫ مقدمه
-
ما یک شبکه کانولوشن انتشار گراف دو فازی طراحی میکنیم که میتواند به طور موثر محدودیتهای شبکههای عصبی کانولوشن گراف را برطرف کند. در طول فرآیند انتشار پیچیدگی، ما از دو نوع ماتریس مجاورت استفاده میکنیم و مکانیسم توجه را برای گرفتن وابستگیهای فضایی پویا به صورت تطبیقی معرفی میکنیم.
-
پیچیدگی علتی گشاد شده ترکیبی برای گرفتن وابستگیهای زمانی استفاده میشود، که میتواند مشکل اثر شبکه پیچیدگی متسع معمولی را برطرف کند. ما از مکانیزم دروازهای برای کنترل کارآمد جریان اطلاعات گرهها و در نظر گرفتن دورهای دادههای تقاضای تاکسی استفاده میکنیم.
-
ما رویکرد خود را بر روی دو مجموعه داده دنیای واقعی در مقیاس بزرگ ارزیابی کردیم. نتایج تجربی نشان میدهد که ST-DCN از هفت روش پایه موجود برتری دارد.
۲٫ مقدماتی
پیش بینی تقاضای تاکسی: با توجه به یک نمودار G=(V,E,A)، جایی که V مجموعه ای از گره های گراف را نشان می دهد ( |V|=N) که ایستگاه های مجازی هستند. E مجموعه ای از لبه ها است که نشان دهنده ارتباط بین گره ها است. A∈RN×Nیک ماتریس مجاورت وزنی از نمودار است که در آن هر عنصر وجود دارد Aijوزنی را ذخیره می کند که نشان دهنده قدرت اتصال بین گره i و j است. در مرحله زمانی t ، نمودار G یک سیگنال گراف دارد Xt∈RN×C، C تعداد ابعاد ویژگی ورودی است. دو ویژگی در نظر گرفته شده است، از جمله تعداد برداشت و رها کردن هر گره در مرحله زمانی t . با توجه به نمودار G و تاریخچه سیگنالهای نمودار مرحله زمانی H ، مسئله پیشبینی تقاضای تاکسی به عنوان یافتن تابع نقشهبرداری f فرموله میشود که میتواند تاکسی را برای مراحل بعدی زمانی P پیشبینی کند . رابطه نگاشت را می توان به صورت زیر تعریف کرد:
جایی که X(t−H+1):t∈RH×N×Cو X(t+1):(t+P)∈RP×N×C.
۳٫ روش شناسی
۳٫۱٫ مدلسازی وابستگی فضایی
این مقاله پیچیدگی انتشار پیشنهاد شده توسط DCRNN [ ۸ ] را اعمال میکند و ماتریس مجاورت خود تطبیقی طراحی شده در Graph WaveNet [ ۱۱ ] را برای مدلسازی وابستگی فضایی به کار میگیرد. به طور خاص، ما استفاده می کنیم A¯¯¯برای نشان دادن ماتریس مجاورت ساکن که در آن هر مقدار فاصله بین دو گره و را ذخیره می کند A˜برای نشان دادن ماتریس مجاورت خود تطبیقی با تعریف زیر
جایی که M1,M2∈RN×cجاسازی گره منبع و هدف هستند، Pماتریس انتقال است، X نشان دهنده ورودی، و W نشان دهنده ماتریس پارامتر مدل است.
معادله ( ۳ ) اثرات مختلف وابستگی های فضایی نشان داده شده توسط ماتریس های مجاورت مختلف را در نظر نمی گیرد، که برای یادگیری موثر وابستگی های فضایی مهم است. به طور مشابه، در فرآیند انتشار کانولوشن، تأثیرات مختلف هر مرحله نیز باید در نظر گرفته شود. بنابراین، ما یک فرآیند انتشار کانولوشن را برای کنترل جریان اطلاعات روی گرهها اتخاذ میکنیم که از دو فاز اصلی تشکیل شده است: مرحله انتشار اطلاعات و مرحله کنترل اطلاعات. مرحله انتشار اطلاعات به صورت زیر تعریف می شود:
جایی که αیک هایپرپارامتر است که برای کنترل میزان نگهداری اطلاعات گره اصلی استفاده می شود. همین رابطه برای ماتریس مجاورت ساکن فقط با جایگزین کردن صدق می کند آ˜با آ¯¯¯در معادله بالا
شبکه های کانولوشن گراف نیز با مشکل هموارسازی بیش از حد مواجه هستند [ ۲۷ ، ۲۸ ]. پس از چندین لایه کانولوشن گراف، ویژگی های گره به بردارهای یکسان یا مشابه همگرا می شوند و آنها را غیر قابل تشخیص می کند. مرحله کنترل اطلاعات برای رسیدگی موثر به این مشکل اتخاذ می شود و می تواند اطلاعات تولید شده توسط گره ها را کنترل کند. در اینجا، ما از مکانیسم توجه [ ۲۹ ] برای کنترل جریان اطلاعات گره ها به صورت تطبیقی استفاده می کنیم. مکانیسم توجه می تواند توجه محدود را بر روی اطلاعات مهم متمرکز کند، بنابراین منابع محاسباتی را ذخیره می کند و به سرعت مفیدترین اطلاعات را به دست می آورد. پس از ترکیب دو مرحله از فرآیند انتشار کانولوشن، معادله ( ۳ ) به معادله زیر تبدیل می شود.۶ ):
که در آن K عمق انتشار اطلاعات، X خروجی مرحله قبلی انتشار اطلاعات است که به عنوان ورودی برای انتشار اطلاعات بعدی استفاده می شود، و W ضریب وزن های خودآموز با استفاده از مکانیسم توجه است.
۳٫۲٫ مدل سازی وابستگی زمانی
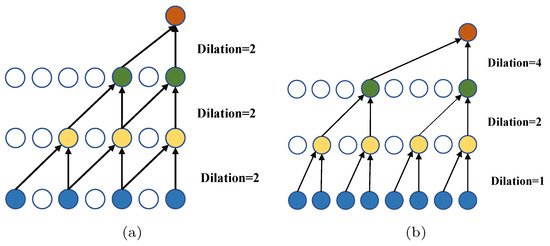
پیچیدگی علت گشاد شده: شبکههای پیچیدگی سببی متسع میتوانند به صورت تصاعدی میدان گیرنده را با قرار دادن عمق لایههای شبکه افزایش دهند. در مقایسه با روشهای مبتنی بر RNN، شبکههای پیچیدگی علّی متسع میتوانند توالیهای طولانیمدت را به شیوهای غیر بازگشتی مقابله کنند، محاسبات موازی را ممکن میسازند و مسئله انفجار گرادیان را کاهش میدهند [ ۳۰ ]. شبکههای کانولوشنی علّی متسع، توالی علیت زمانی را با قرار دادن صفر در ورودیها حفظ میکنند. به این ترتیب، تضمین میکند که فقط اطلاعات تاریخی برای پیشبینی بدون درز اطلاعات آینده استفاده میشود. به طور رسمی تر، برای یک توالی یک بعدی از ورودی ها ایکس∈آرتیو فیلتر f: { ۰ , … , n − ۱ }، عملیات پیچش اتساع F در دنباله ورودی با عنصر t را می توان به صورت زیر تعریف کرد:
که در آن d میزان اتساع، n اندازه فیلتر و t – d⋅ منجهت گذشته را نشان می دهد.
-
نرخ اتساع یک پیچش گشاد شده روی هم نباید فاکتور مشترکی بیشتر از ۱ داشته باشد. برای مثال، [۲، ۴، ۶] پیچیدگی سه لایه مناسبی نخواهد بود، زیرا هنوز اثرات شبکهبندی دارد.
-
نرخ اتساع به عنوان یک ساختار ناهموار طراحی شده است، به عنوان مثال، یک ساختار چرخه ای مانند [۱، ۲، ۵، ۱، ۲، ۵].
-
نرخ اتساع باید معادله را برآورده کند:
ممن= m a x (ممن + ۱– ۲دمن،ممن + ۱− ۲ (ممن + ۱–دمن) ،دمن)
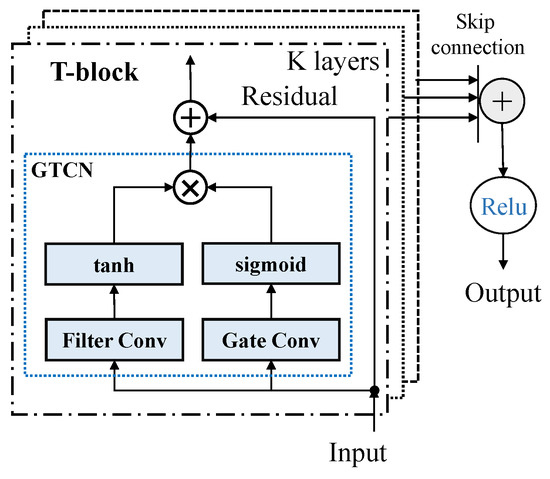
TCN دردار: ما از TCN دردار طراحی شده توسط Graph WaveNet [ ۱۱ ] برای کنترل جریان اطلاعات معتبر و دور انداختن اطلاعات نامعتبر در TCN استفاده می کنیم. یک پیچیدگی زمانی توسط یک تابع فعال سازی هذلولی مماس که به عنوان یک فیلتر کار می کند دنبال می شود. پیچیدگی زمانی دیگر توسط یک تابع فعال سازی سیگموئید دنبال می شود که به عنوان دروازه ای برای کنترل مقدار اطلاعات در حال انتشار عمل می کند. به طور خاص، Gated TCN به شکل زیر است:
جایی که Θ۱,Θ۲,b1و b2پارامترهای قابل یادگیری هستند، ⊙ عملگر ضرب المان را نشان می دهد، σ(⋅)یک تابع سیگموئید است، ∗ عملیات پیچش گشاد شده است. شکل ۶ ساختار TCN دردار را نشان می دهد.
۳٫۳٫ اجزای اضافی
۴٫ آزمایشات
۴٫۱٫ تنظیمات آزمایشی
-
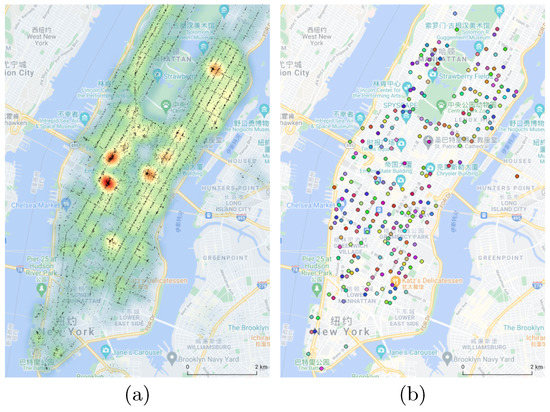
تاکسی نیویورک ( https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page (دسترسی در ۵ مه ۲۰۲۱)): این مجموعه داده شامل ۹۱ روز از ۳۵ میلیون سوابق سفر تاکسی نیویورک است. در تاکسی های زرد از ۱ آوریل ۲۰۱۶ تا ۳۰ ژوئن ۲۰۱۶٫
-
Didi Taxi ( https://outreach.didichuxing.com/research/opendata/en/ (دسترسی در ۷ ژوئیه ۲۰۲۱)): مجموعه داده شامل درخواست تاکسی از ۱ نوامبر ۲۰۱۶ تا ۳۰ نوامبر ۲۰۱۶ برای شهر چنگدو با بیش از ۷ درخواست است. میلیون رکورد سفر تاکسی
۴٫۲٫ خطوط پایه
-
LSTM [ ۳۴ ]: شبکه حافظه کوتاه مدت بلند مدت، یک مدل RNN ویژه برای پیش بینی سری های زمانی.
-
DCRNN [ ۸ ]: شبکه عصبی بازگشتی کانولوشن انتشار، که شبکههای کانولوشنی گراف انتشار را با GRU به روش رمزگذار-رمزگشا ترکیب میکند.
-
STGCN [ ۳۵ ]: یک شبکه کانولوشنال نمودار مکانی-زمانی از کانولوشن گراف ChebNet و شبکههای کانولوشنیک ۱ بعدی برای گرفتن وابستگیهای مکانی و همبستگیهای زمانی استفاده میکند.
-
GWNet [ ۱۱ ]: یک شبکه کانولوشنال نمودار مکانی-زمانی، ماتریس مجاورت تطبیقی را در پیچیدگیهای نمودار انتشار با پیچیدگیهای معمولی گشادشده ۱ بعدی ادغام میکند.
-
ASTGCN [ ۹ ]: شبکههای کانولوشنال نمودار مکانی-زمانی مبتنی بر توجه، که مکانیسمهای توجه مکانی و توجه زمانی را به ترتیب برای مدلسازی دینامیک مکانی و زمانی معرفی میکند. برای انصاف، ما فقط اجزای اخیر آن را در نظر می گیریم.
-
MTGNN [ ۳۶ ]: یک شبکه عصبی گراف که برای پیشبینی سریهای زمانی چند متغیره با افزودن یک لایه یادگیری نمودار طراحی شده است تا روابط پنهان میان دادههای سری زمانی را به تصویر بکشد.
-
CCRNN [ ۲۲ ]: یک پیچیدگی نمودار لایهای جفت که برای پیشبینی تقاضای حملونقل طراحی شده است.
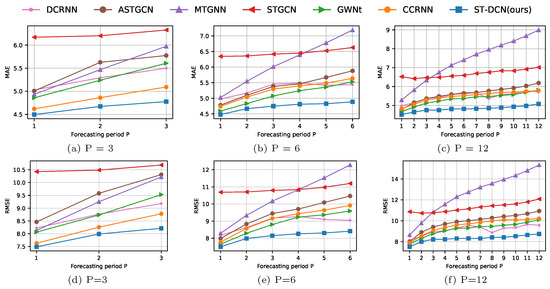
۴٫۳٫ مقایسه عملکرد
۴٫۴٫ تجزیه و تحلیل مولفه
-
پایه: این مدل به پیچیدگی اتساع هیبریدی، پیچیدگی انتشار نمودار دو فازی و تناوب زمانی مجهز نیست.
-
+HDC: این مدل از پیچش گشاد شده هیبریدی برای غلبه بر اثر شبکهبندی استفاده میکند.
-
دو فازی: این مدل از پیچش انتشار گراف دو فازی برای رسیدگی به دو محدودیت پیچیدگی گراف استفاده میکند، اما از پیچیدگی گشاد شده ترکیبی استفاده نمیکند.
-
یک T-block (1 روز): این مدل دوره روزانه را در یک T-block در نظر می گیرد (فقط دیروز شامل می شود).
-
مولتی تی بلوک (۱ روز): این مدل دوره روزانه را در چند بلوک T در نظر می گیرد (فقط دیروز شامل می شود).
-
یک T-block (7 روز): این مدل دوره روزانه و هفتگی را در یک T-block در نظر می گیرد.
-
ST-DCN (مولتی T-block (7 روز)): این مدل دوره روزانه و هفتگی را در چند بلوک T در نظر می گیرد. این نسخه کامل رویکرد پیشنهادی ما ST-DCN است.
۵٫ بحث
۶٫ نتیجه گیری و کار آینده
منابع
- ژانگ، جی. ژنگ، ی. Qi، D. شبکههای باقیمانده مکانی-زمانی عمیق برای پیشبینی جریانهای جمعیتی در سطح شهر. در مجموعه مقالات AAAI، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، ۴ تا ۹ فوریه ۲۰۱۷؛ صفحات ۱۶۵۵-۱۶۶۱٫ [ Google Scholar ]
- سان، ج. ژانگ، جی. لی، کیو. یی، ایکس. لیانگ، ی. ژنگ، ی. پیشبینی جریانهای جمعیت در سطح شهر در مناطق نامنظم با استفاده از شبکههای کانولوشن گراف چند نمای. IEEE Trans. دانستن مهندسی داده ۲۰۲۰ ، ۱۴ . [ Google Scholar ] [ CrossRef ]
- یائو، اچ. وو، اف. که، جی. تانگ، ایکس. جیا، ی. لو، اس. گونگ، پی. لی، ز. بله، جی. Chuxing، D. شبکه چند نمای عمیق فضایی-زمانی برای پیش بینی تقاضای تاکسی. arXiv ۲۰۱۸ , arXiv:1802.08714. [ Google Scholar ]
- گنگ، ایکس. لی، ی. وانگ، ال. ژانگ، ال. یانگ، کیو. بله، جی. لیو، ی. شبکه پیچیدگی چند نموداری فضایی-زمانی برای پیشبینی تقاضای تگرگ سواری. در مجموعه مقالات AAAI، هونولولو، HI، ایالات متحده آمریکا، ۲۷ ژانویه تا ۱ فوریه ۲۰۱۹؛ جلد ۳۳، ص ۳۶۵۶–۳۶۶۳٫ [ Google Scholar ]
- بای، ال. یائو، ال. Kanhere, SS; وانگ، ایکس. شنگ، QZ STG2seq: نمودار مکانی-زمانی به مدل توالی برای پیشبینی تقاضای مسافر چند مرحلهای. IJCAI ۲۰۱۹ ، ۱۹۸۱-۱۹۸۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لیو، ال. کیو، ز. لی، جی. وانگ، کیو. اویانگ، دبلیو. لین، ال. شبکه فضایی زمینهای برای پیشبینی تقاضای مبدا و مقصد تاکسی. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۹ ، ۲۰ ، ۳۸۷۵–۳۸۸۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- وانگ، ی. وو، تی. یین، اچ. خو، جی. چن، اچ. ژنگ، ک. پیشبینی ماتریس مبدا-مقصد از طریق پیچیدگی نمودار: دیدگاه جدیدی از مدلسازی تقاضای مسافر. در مجموعه مقالات بیست و پنجمین کنفرانس ACM SIGKDD در مورد کشف دانش و داده کاوی، Anchorage، AK، ایالات متحده آمریکا، ۴ تا ۸ اوت ۲۰۱۹؛ ص ۱۲۲۷–۱۲۳۵٫ [ Google Scholar ] [ CrossRef ]
- لی، ی. یو، آر. شهابی، ج. لیو، ی. شبکه عصبی تکراری کانولوشنال انتشار: پیشبینی ترافیک مبتنی بر داده. arXiv ۲۰۱۸ , arXiv:1707.01926. [ Google Scholar ]
- گوا، اس. لین، ی. فنگ، ن. آهنگ، سی. وان، اچ. شبکههای کانولوشنال نمودار مکانی-زمانی مبتنی بر توجه برای پیشبینی جریان ترافیک. در مجموعه مقالات AAAI، هونولولو، HI، ایالات متحده آمریکا، ۲۷ ژانویه تا ۱ فوریه ۲۰۱۹؛ جلد ۳۳، ص ۹۲۲–۹۲۹٫ [ Google Scholar ]
- ژائو، ال. آهنگ، ی. ژانگ، سی. لیو، ی. وانگ، پی. لین، تی. دنگ، م. Li، H. T-gcn: یک شبکه کانولوشن گراف زمانی برای پیشبینی ترافیک. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۹ ، ۲۱ ، ۳۸۴۸–۳۸۵۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- وو، زی. پان، اس. لانگ، جی. جیانگ، جی. ژانگ، سی. موج موج گراف برای مدلسازی نمودار عمیق مکانی-زمانی. IJCAI ۲۰۱۹ ، ۱۹۰۷–۱۹۱۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- شی، ایکس. چی، اچ. شن، ی. وو، جی. یین، ب. رویکرد توجه مکانی-زمانی برای پیشبینی ترافیک. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۲۰ ، ۲۲ ، ۴۹۰۹-۴۹۱۸٫ [ Google Scholar ] [ CrossRef ]
- یائو، اچ. تانگ، ایکس. وی، اچ. ژنگ، جی. لی، زی. بازبینی شباهت مکانی-زمانی: یک چارچوب یادگیری عمیق برای پیشبینی ترافیک. در مجموعه مقالات AAAI، هونولولو، HI، ایالات متحده آمریکا، ۲۷ ژانویه تا ۱ فوریه ۲۰۱۹؛ جلد ۳۳، ص ۵۶۶۸–۵۶۷۵٫ [ Google Scholar ]
- آهنگ، سی. لین، ی. گوا، اس. وان، اچ. شبکه های کانولوشن گراف همزمان مکانی-زمانی: چارچوبی جدید برای پیش بینی داده های شبکه مکانی-زمانی. در مجموعه مقالات AAAI، نیویورک، نیویورک، ایالات متحده آمریکا، ۷ تا ۱۲ فوریه ۲۰۲۰؛ ص ۹۱۴-۹۲۱٫ [ Google Scholar ] [ CrossRef ]
- ژانگ، ایکس. هوانگ، سی. خو، ی. شیا، ال. دای، پی. بو، ال. ژانگ، جی. ژنگ، ی. پیشبینی جریان ترافیک با شبکه انتشار نمودار مکانی-زمانی. در مجموعه مقالات AAAI، مجازی، ۲ تا ۹ فوریه ۲۰۲۱؛ جلد ۳۵، ص ۱۵۰۰۸–۱۵۰۱۵٫ [ Google Scholar ]
- لی، ام. Zhu, Z. شبکه های عصبی نمودار فیوژن مکانی-زمانی برای پیش بینی جریان ترافیک. در مجموعه مقالات AAAI، مجازی، ۲ تا ۹ فوریه ۲۰۲۱؛ جلد ۳۵، ص ۴۱۸۹–۴۱۹۶٫ [ Google Scholar ]
- لین، ال. او، ز. پیتا، اس. پیشبینی تقاضای ساعتی سطح ایستگاه در یک شبکه اشتراکگذاری دوچرخه در مقیاس بزرگ: یک رویکرد شبکه عصبی کانولوشنال گراف. ترانسپ Res. قسمت C Emerg. تکنولوژی ۲۰۱۸ ، ۹۷ ، ۲۵۸-۲۷۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ژانگ، سی. زو، اف. Lv، Y.; بله، پی. وانگ، FY MLRNN: پیشبینی تقاضای تاکسی بر اساس یادگیری عمیق چند سطحی و تحلیل ناهمگونی منطقهای. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۲۱ ، ۱-۱۱٫ [ Google Scholar ] [ CrossRef ]
- کالتن برونر، آ. مزا، ر. گریولا، جی. کودینا، جی. Banchs، R. چرخه های شهری و الگوهای تحرک: کاوش و پیش بینی روندها در یک سیستم حمل و نقل عمومی مبتنی بر دوچرخه. اوباش فراگیر. محاسبه کنید. ۲۰۱۰ ، ۶ ، ۴۵۵-۴۶۶٫ [ Google Scholar ] [ CrossRef ]
- موریرا-ماتیاس، ال. گاما، ج. فریرا، م. مندس موریرا، جی. Damas, L. پیش بینی تقاضای تاکسی-مسافر با استفاده از داده های جریانی. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۳ ، ۱۴ ، ۱۳۹۳–۱۴۰۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ویلیامز، بی.ام. Hoel، LA مدلسازی و پیش بینی جریان ترافیک وسایل نقلیه به عنوان یک فرآیند ARIMA فصلی: مبنای نظری و نتایج تجربی. J. Transp. مهندس ۲۰۰۳ ، ۱۲۹ ، ۶۶۴-۶۷۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- بله، جی. سان، ال. دو، بی. فو، ی. Xiong، H. پیچیدگی نمودار لایهای برای پیشبینی تقاضای حملونقل. در مجموعه مقالات AAAI، مجازی، ۲ تا ۹ فوریه ۲۰۲۱؛ جلد ۳۵، ص ۴۶۱۷–۴۶۲۵٫ [ Google Scholar ]
- دو، بی. هو، ایکس. سان، ال. لیو، جی. کیائو، ی. Lv، W. پیشبینی تقاضای ترافیک بر اساس شبکه عصبی کانولوشنال انتقال پویا. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۲۰ ، ۲۲ ، ۱۲۳۷-۱۲۴۷٫ [ Google Scholar ] [ CrossRef ]
- رودریگز، آ. Laio، A. خوشه بندی با جستجوی سریع و یافتن قله های چگالی. Science ۲۰۱۴ ، ۳۴۴ ، ۱۴۹۲-۱۴۹۶٫ [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
- او، ک. ژانگ، ایکس. رن، اس. Sun, J. یادگیری باقیمانده عمیق برای تشخیص تصویر. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو، لاس وگاس، NE، ایالات متحده آمریکا، ۲۷ تا ۳۰ ژوئن ۲۰۱۶٫ صص ۷۷۰-۷۷۸٫ [ Google Scholar ]
- آلون، یو. Yahav, E. On the Bottleneck of Graph Neural Networks and Perfectives It. در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی های یادگیری، آدیس آبابا، اتیوپی، ۲۶ تا ۳۰ آوریل ۲۰۲۰٫ [ Google Scholar ]
- اونو، ک. سوزوکی، T. گراف شبکه های عصبی به طور نمایی قدرت بیانی را برای طبقه بندی گره از دست می دهند در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی یادگیری، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، ۶ تا ۹ مه ۲۰۱۹٫ [ Google Scholar ]
- لی، کیو. هان، ز. بینش Wu، XM Deeper در مورد شبکه های کانولوشن گراف برای یادگیری نیمه نظارت شده. در مجموعه مقالات سی و دومین کنفرانس AAAI در مورد هوش مصنوعی، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، ۲ تا ۷ فوریه ۲۰۱۸٫ [ Google Scholar ]
- واسوانی، ع. Shazeer، N. پارمار، ن. Uszkoreit، J. جونز، ال. گومز، AN; قیصر، Ł. Polosukhin، I. توجه شما تمام چیزی است که نیاز دارید. Adv. عصبی Inf. روند. سیستم ۲۰۱۷ ، ۳۰ ، ۵۹۹۹-۶۰۰۹٫ [ Google Scholar ]
- بای، اس. Kolter، JZ; کلتون، وی. ارزیابی تجربی شبکههای کانولوشنال و تکراری عمومی برای مدلسازی توالی. arXiv ۲۰۱۸ , arXiv:1803.01271. [ Google Scholar ]
- وانگ، پی. چن، پی. یوان، ی. لیو، دی. هوانگ، ز. هو، ایکس. کاترل، جی. درک پیچیدگی برای تقسیم بندی معنایی. در مجموعه مقالات کنفرانس زمستانی IEEE 2018 در مورد کاربردهای بینایی کامپیوتری (WACV)، دریاچه تاهو، NV، ایالات متحده، ۱۲ تا ۱۵ مارس ۲۰۱۸؛ ص ۱۴۵۱-۱۴۶۰٫ [ Google Scholar ]
- اورهان، ای. Pitkow, X. اتصالات را پرش کنید تکینگی ها را حذف کنید. در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی های یادگیری، ونکوور، بریتیش کلمبیا، کانادا، ۳۰ آوریل تا ۳ مه ۲۰۱۸٫ [ Google Scholar ]
- Kingma، DP; Ba, J. Adam: روشی برای بهینه سازی تصادفی. arXiv ۲۰۱۴ ، arXiv:1412.6980. [ Google Scholar ]
- هوکرایتر، اس. Schmidhuber, J. حافظه کوتاه مدت طولانی. محاسبات عصبی ۱۹۹۷ ، ۹ ، ۱۷۳۵-۱۷۸۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
- یو، بی. یین، اچ. Zhu, Z. شبکههای کانولوشنال نمودار فضایی-زمانی: یک چارچوب یادگیری عمیق برای پیشبینی ترافیک. arXiv ۲۰۱۷ , arXiv:1709.04875. [ Google Scholar ]
- وو، زی. پان، اس. لانگ، جی. جیانگ، جی. چانگ، ایکس. ژانگ، سی. اتصال نقاط: پیشبینی سریهای زمانی چند متغیره با شبکههای عصبی نمودار. arXiv ۲۰۲۰ ، arXiv:2005.11650، ۷۵۳–۷۶۳٫ [ Google Scholar ]