کلید واژه ها:
تشخیص خوشه فضایی ; رویداد نقطه ای ; استنتاج بیزی مدلسازی پراکنده ; کمند ذوب شده عمومی
۱٫ مقدمه
۲٫ تشخیص خوشه مبتنی بر مدلسازی پراکنده
۲٫۱٫ کمند ذوب شده و کمند ذوب شده تعمیم یافته
مسئله کمینه سازی برای یک مدل رگرسیون خطی با کمند ذوب شده به صورت زیر فرموله شده است:
جایی که ∥⋅∥۲هنجار L2 است، y=(y1,⋯,yn)⊤یک بردار متغیر وابسته است و X=(x1,⋯,xp)یک ماتریس طراحی است. λ۱و λ۲فراپارامترهایی هستند که بر درجات تنظیم L1 حاکم هستند.
کمند ذوب شده تعمیم یافته به صورت زیر نوشته می شود:
جایی که سیمجموعه ای از جفت پارامترهای مجاور است.
۲٫۲٫ تشخیص خوشهای مبتنی بر مدلسازی پراکنده
چوی و همکاران [ ۱۲ ] تشخیص خوشهای را از توزیع فضایی رویدادهای نقطهای جمعآوری شده در مناطق کوچک با معرفی جریمه کمند ذوب شده تعمیم یافته در مدل رگرسیون پواسون فرمولبندی کرد. اول، تعداد رویدادهای نقطه ای ثبت شده در یک زیر منطقه i ( i = ۱ ، ⋯ ، n) به صورت زیر بیان می شود:
جایی که همنیک اصطلاح افست برای زیرمنطقه i است ، xi=(1,xi1,⋯,xip)⊤یک بردار کمکی است و β=(β۰,⋯,βp)⊤بردار پارامتر مربوطه است که توسط کل منطقه مورد مطالعه مشترک است. α=(α۱,⋯,αn)⊤نشان دهنده یک بردار متشکل از پارامترهای شدت مبتنی بر زیرمنطقه است که درجه غلظت را برای هر زیر منطقه نشان می دهد. اگر ارزش تخمینی از αiبرابر با صفر است، منطقه فرعی i یک خوشه را تشکیل نمی دهد، و اگر مقادیر تخمینی αiبزرگتر از صفر هستند، سپس منطقه فرعی i یک خوشه را تشکیل می دهد.
در اینجا تابع درستنمایی پواسون است L(α,β|X,Y)و تابع لاگ درستنمایی پواسون l(α,β|X,Y)توسط:
جایی که Xو Yمجموعه ای از داده های مشاهده شده هستند که به صورت تعریف شده اند X=(x1,⋯,xn)⊤و Y=(y1,⋯,yn)⊤، به ترتیب.
با معرفی جریمه کمند ذوب شده تعمیم یافته به تابع لگاریتم درستنمایی پواسون، مسئله تشخیص خوشه [ ۱۲ ] را می توان به صورت زیر فرموله کرد:
جایی که Cمجموعه ای از جفت پارامترهای مجاور است و λ۱,λ۲,و λ۳هایپرپارامترها هستند.
۳٫ مطالعات قبلی در مورد پیشینیان پراکنده
۳٫۱٫ کمند بیزی
تیبشیرانی [ ۱۵ ] ابتدا پیشنهاد کرد که در مدلهای رگرسیون خطی، قرار دادن توزیعهای لاپلاس مستقل به عنوان توزیعهای قبلی برای ضرایب رگرسیون میتواند توزیعهای خلفی را به سمت صفر کوچک کند و تخمینهای کمند را در حالتهای پسینی کاهش دهد. به دنبال این مفهوم، پارک و کازلا [ ۱۶ ] فرمول نمونهگیری گیبس را برای مدلهای بیزی با توزیع لاپلاس پیشنهاد کردند و آن را «کند بیزی» نامیدند. معادله ( ۸ ) توزیع لاپلاس را به عنوان یک پیشین القا کننده پراکندگی نشان می دهد، همانطور که در [ ۱۶ ] پیشنهاد شده است:
جایی که β=(β۱,⋯,βp)⊤بردار متغیر کمکی است و λیک هایپرپارامتر قابل مقایسه با پارامتر تنظیم در کمند است. پارک و کازلا [ ۱۶ ] بیان کردند که با فرض پیشبینی نامناسب σ۲می تواند در برخی موارد از چند حالت خلفی اجتناب کند.
۳٫۲٫ کمند ذوب شده تعمیم یافته بیزی
کیونگ و همکاران [ ۱۷ ] کمند بیزی را گسترش داد و کمند ذوب شده بیزی را برای مدلهای رگرسیون خطی پیشنهاد کرد. ضرایب رگرسیون قبلی فرموله شده به صورت زیر بدست می آید:
جایی که λ۱و λ۲هایپرپارامتر هستند.
معادله ( ۹ ) را می توان به راحتی به کمند ذوب شده تعمیم یافته بیزی تعمیم داد که فرمول آن شامل چندین توزیع لاپلاس است و به صورت زیر نوشته می شود:
جایی که سیمجموعه ای از جفت پارامترهای مجاور است.
۴٫ روش پیشنهادی
۴٫۱٫ احتمال و توزیع های قبلی
با فرض فرآیند نقطه پواسون، تعداد نقاط yمنتوسط مدل رگرسیون پواسون زیر ارائه می شود:
پس از آن، تابع درستنمایی پواسون معادله ( ۱۱ ) را می توان به صورت زیر نوشت:
جایی که ایکسو Yمجموعه ای از داده های مشاهده شده تعریف شده توسط ایکس=(ایکس۱، ⋯ ،ایکسn)⊤و Y=(y1، ⋯ ،yn)⊤، به ترتیب.
اکنون، توزیع قبلی مشترک را برای بردار پارامتر شدت تعریف می کنیم αو بردار متغیر β˜مانند:
جایی که Cمجموعه ای از جفت پارامترهای مجاور است و λ۱,λ۲,و λ۳هایپرپارامترها هستند. در این مطالعه، مجاورت به عنوان یک جفت زیرمنطقه که مرزهای جغرافیایی مشترک دارند، تعریف شده است.
۴٫۲٫ تنظیم فراپارامترها با معیار اطلاعات Watanabe-Akaike
۵٫ ارزیابی
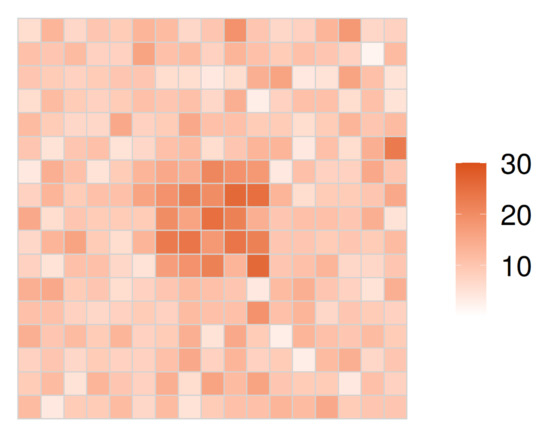
۵٫۱٫ ارزیابی با توزیع های شبیه سازی شده
۵٫۱٫۱٫ بررسی اجمالی
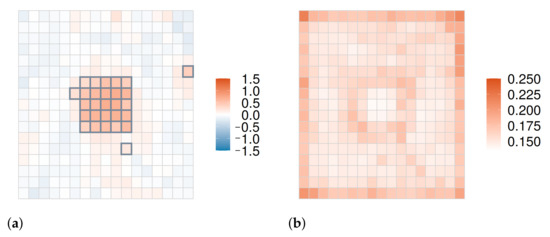
توزیعهای خلفی نمونهبرداری شده از پارامترهای شدت تعیین میکنند که آیا هر زیرمنطقه یک خوشه را تشکیل میدهد یا خیر. احتمال آستانه p از قبل تنظیم شده بود، و اگر مقدار نقطه درصد پایین p پارامتر شدت تخمینی اختصاص داده شده به یک منطقه فرعی از صفر بیشتر شود، آن منطقه فرعی به عنوان یک خوشه تشخیص داده می شود. در این مطالعه، p=0.1برای احتمال آستانه پذیرفته شد زیرا طبقه بندی خوشه ای با این آستانه نتایجی قابل مقایسه با روش چوی ایجاد کرد. از نتایج خوشهبندی برای همه زیرمنطقهها، ما دو معیار عملکرد، یعنی توان و نرخ مثبت کاذب را محاسبه کردیم که معمولاً یک رابطه مبادله دارند. تعاریف آنها به شرح زیر است:
۵٫۱٫۲٫ نتایج
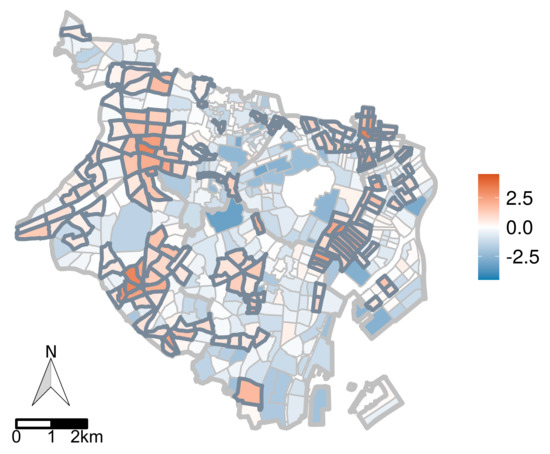
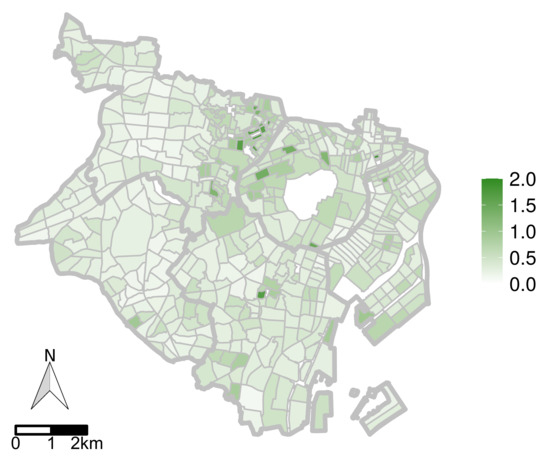
۵٫۲٫ ارزیابی با داده های دنیای واقعی
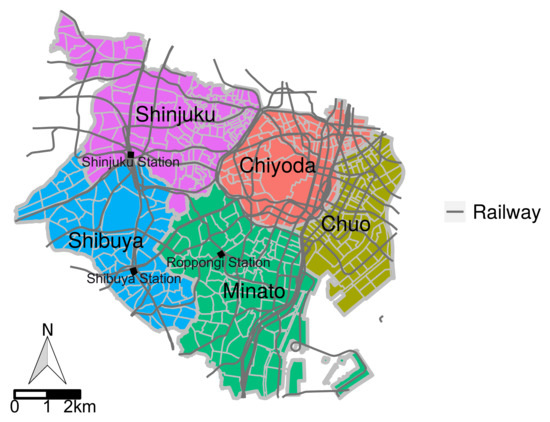
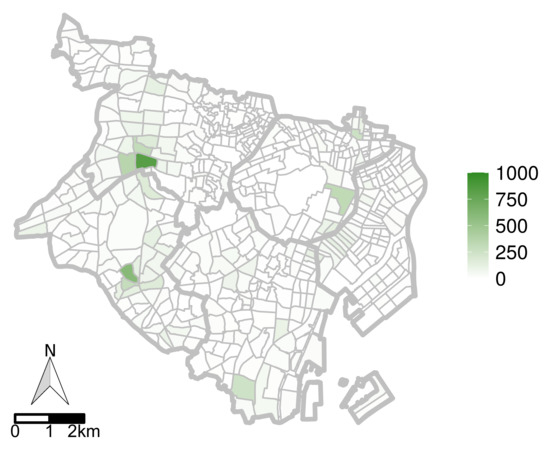
۵٫۲٫۱٫ منطقه هدف و توصیف داده ها
۵٫۲٫۲٫ تنظیمات تخمین
۵٫۲٫۳٫ نتایج
۵٫۳٫ بحث
۶٫ نتیجه گیری
مشارکت های نویسنده
منابع مالی
بیانیه در دسترس بودن داده ها
تضاد علاقه
منابع
- گتیس، ع. Ord, JK تجزیه و تحلیل ارتباط فضایی با استفاده از آمار فاصله. Geogr. مقعدی ۱۹۹۲ ، ۲۴ ، ۱۸۹-۲۰۶٫ [ Google Scholar ] [ CrossRef ]
- Anselin، L. شاخص های محلی ارتباط فضایی-LISA. Geogr. مقعدی ۱۹۹۵ ، ۲۷ ، ۹۳-۱۱۵٫ [ Google Scholar ] [ CrossRef ]
- کولدورف، ام. Nagarwalla، N. خوشه های بیماری فضایی: تشخیص و استنتاج. آمار پزشکی ۱۹۹۵ ، ۱۴ ، ۷۹۹-۸۱۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Kulldorff, M. SaTScan v10.0.2: نرم افزاری برای آمار اسکن مکانی، زمانی و فضا-زمان. ۲۰۲۲٫ در دسترس آنلاین: https://www.satscan.org/ (دسترسی در ۲۵ فوریه ۲۰۲۲).
- هوانگ، ال. کولدورف، ام. گرگوریو، دی. آمار اسکن فضایی برای داده های بقا. بیومتریک ۲۰۰۷ ، ۶۳ ، ۱۰۹-۱۱۸٫ [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
- یونگ، I. آمار اسکن فضایی برای داده های مورد-شاهد همسان. PLoS ONE ۲۰۱۹ , ۱۴ , e0221225. [ Google Scholar ] [ CrossRef ]
- تاکاهاشی، ک. Shimadzu، H. تشخیص خوشه های بیماری فضایی متعدد: معیار اطلاعات و رویکرد آماری اسکن. بین المللی J. Health Geogr. ۲۰۲۰ ، ۱۹ ، ۱-۱۱٫ [ Google Scholar ] [ CrossRef ]
- دوکزمال، ال. Assuncao، R. یک استراتژی بازپخت شبیه سازی شده برای تشخیص خوشه های فضایی با شکل دلخواه. محاسبه کنید. آمار داده آنال. ۲۰۰۴ ، ۴۵ ، ۲۶۹-۲۸۶٫ [ Google Scholar ] [ CrossRef ]
- دوکزمال، ال. Cançado، AL; تاکاهاشی، RH; Bessegato، LF یک الگوریتم ژنتیک برای آمار اسکن فضایی با شکل نامنظم. محاسبه کنید. آمار داده آنال. ۲۰۰۷ ، ۵۲ ، ۴۳-۵۲٫ [ Google Scholar ] [ CrossRef ]
- کالداس د کاسترو، م. سینگر، BH کنترل نرخ کشف نادرست: یک برنامه کاربردی جدید برای محاسبه تستهای متعدد و وابسته در آمار محلی تداعی فضایی. Geogr. مقعدی ۲۰۰۶ ، ۳۸ ، ۱۸۰-۲۰۸٫ [ Google Scholar ] [ CrossRef ]
- براندون، سی. چارلتون، ام. ارزیابی اثربخشی آزمون فرضیههای چندگانه برای تشخیص ناهنجاری جغرافیایی. محیط زیست طرح. طرح. دس ۲۰۱۱ ، ۳۸ ، ۲۱۶-۲۳۰٫ [ Google Scholar ] [ CrossRef ]
- چوی، اچ. آهنگ، ای. هوانگ، اس اس؛ Lee, W. یک الگوریتم کمند تعمیم یافته اصلاح شده برای تشخیص خوشه های فضایی محلی برای داده های شمارش. ASTA Adv. آمار مقعدی ۲۰۱۸ ، ۱۰۲ ، ۵۳۷-۵۶۳٫ [ Google Scholar ] [ CrossRef ]
- طبشیرانی، ر.ج. Taylor, J. مسیر حل کمند تعمیم یافته. ان آمار ۲۰۱۱ ، ۳۹ ، ۱۳۳۵-۱۳۷۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هانتر، DR. Li, R. انتخاب متغیر با استفاده از الگوریتم های MM. ان آمار ۲۰۰۵ ، ۳۳ ، ۱۶۱۷-۱۶۴۲٫ [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
- تیبشیرانی، انقباض و انتخاب رگرسیون RJ از طریق کمند. JR Stat. Soc. سر. B (Methodol.) ۱۹۹۶ ، ۵۸ ، ۲۶۷-۲۸۸٫ [ Google Scholar ] [ CrossRef ]
- پارک، تی. کازلا، جی. کمند بیزی. مربا. آمار دانشیار ۲۰۰۸ ، ۱۰۳ ، ۶۸۱-۶۸۶٫ [ Google Scholar ] [ CrossRef ]
- کیونگ، ام. گیل، جی. قوش، م. Casella، G. رگرسیون مجازات، خطاهای استاندارد، و کمند بیزی. مقعد بیزی. ۲۰۱۰ ، ۵ ، ۳۶۹-۴۱۱٫ [ Google Scholar ]
- طبشیرانی، ر. ساندرز، ام. راست، اس. ژو، جی. Knight، K. پراکندگی و صافی از طریق کمند ذوب شده. JR Stat. Soc. سر. B (Stat. Methodol.) ۲۰۰۵ ، ۶۷ ، ۹۱-۱۰۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- اینو، آر. ایشیاما، آر. سوگیورا، الف. شناسایی تقسیم بندی جغرافیایی بازار مسکن اجاره ای در منطقه شهری توکیو توسط کمند ذوب شده تعمیم یافته. J. Jpn. Soc. مدنی مهندس سر. D3 (Infrastruct. Plan. Manag.) ۲۰۲۰ ، ۷۶ ، ۲۵۱-۲۶۳٫ (به ژاپنی) [ Google Scholar ] [ CrossRef ]
- اینو، آر. ایشیاما، آر. Sugiura، A. شناسایی تفاوت های محلی با fused-MCP: مطالعه موردی بازار اجاره آپارتمان در تشخیص تقسیم بندی جغرافیایی. Jpn. J. Stat. اطلاعات علمی ۲۰۲۰ ، ۳ ، ۱۸۳-۲۱۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Akaike, H. نگاهی جدید به شناسایی مدل آماری. IEEE Trans. خودکار کنترل. ۱۹۷۴ ، ۱۹ ، ۷۱۶-۷۲۳٫ [ Google Scholar ] [ CrossRef ]
- شوارتز، جی. برآورد ابعاد یک مدل. ان آمار ۱۹۷۸ ، ۶ ، ۴۶۱-۴۶۴٫ [ Google Scholar ] [ CrossRef ]
- واتانابه، اس. هم ارزی مجانبی اعتبار متقاطع بیز و معیار اطلاعاتی به طور گسترده در نظریه یادگیری منفرد. جی. ماخ. فرا گرفتن. Res. ۲۰۱۰ ، ۱۱ ، ۳۵۷۱-۳۵۹۴٫ [ Google Scholar ]
- گلمن، ا. هوانگ، جی. Vehtari, A. درک معیارهای اطلاعات پیش بینی برای مدل های بیزی. آمار محاسبه کنید. ۲۰۱۴ ، ۲۴ ، ۹۹۷-۱۰۱۶٫ [ Google Scholar ] [ CrossRef ]
- دوان، اس. کندی، AD; پندلتون، بیجی؛ روث، دی. هیبرید مونت کارلو. فیزیک Lett. B ۱۹۸۷ ، ۱۹۵ ، ۲۱۶-۲۲۲٫ [ Google Scholar ] [ CrossRef ]
- گلمن، ا. استنتاج روبین، DB از شبیه سازی تکراری با استفاده از توالی های متعدد. آمار علمی ۱۹۹۲ ، ۷ ، ۴۵۷-۴۷۲٫ [ Google Scholar ] [ CrossRef ]
- Shiode، S. آمار اسکن فضایی در سطح خیابان و STAC برای تجزیه و تحلیل غلظت جرایم خیابانی. ترانس. GIS ۲۰۱۱ ، ۱۵ ، ۳۶۵-۳۸۳٫ [ Google Scholar ] [ CrossRef ]
- فن، جی. Li, R. انتخاب متغیر از طریق احتمال جریمه شده غیر مقعر و خواص اوراکل آن. مربا. آمار دانشیار ۲۰۰۱ ، ۹۶ ، ۱۳۴۸-۱۳۶۰٫ [ Google Scholar ] [ CrossRef ]
- گریفین، جی. براون، PJ Bayesian hyper-lassos با پنالتی غیر محدب. اوست آمار NZJ ۲۰۱۱ ، ۵۳ ، ۴۲۳-۴۴۲٫ [ Google Scholar ] [ CrossRef ]
- کاروالیو، سی ام. پولسون، NG; اسکات، جی جی مدیریت پراکندگی از طریق نعل اسب. جی. ماخ. فرا گرفتن. Res. ۲۰۰۹ ، ۵ ، ۷۳-۸۰٫ [ Google Scholar ]
- کاروالیو، سی ام. پولسون، NG; Scott, JG برآوردگر نعل اسبی برای سیگنال های پراکنده. Biometrika ۲۰۱۰ ، ۹۷ ، ۴۶۵-۴۸۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]