بهینه سازی مسیریابی گشت خیابانی در مدیریت شهر هوشمند بر اساس الگوریتم ژنتیک: موردی در ژنگژو، چین

مجموعه ای از رویدادهای اجرای قانون شهری شامل بازرسان شهری که توسط بخش مدیریت شهری اعزام شده اند، می تواند منعکس کننده برخی مشکلات در مدیریت شهر هوشمند، مانند تبلیغات غیرقانونی و عملیات خیابانی بدون مجوز باشد. در این مقاله مدلی برای تخصیص بازرسان شهری و بهینه‌سازی مسیرهای گشت ارائه می‌کنیم. هدف به حداقل رساندن میانگین زمان پاسخگویی و تعداد بازرسان است. ما همچنین یک الگوریتم ژنتیک اولویت‌دار گشت و چند هدفه (DP-MOGA) را برای طبقه‌بندی بخش‌های گشت با توجه به فراوانی رویدادها و توسعه یک الگوریتم ژنتیک بهبودیافته برای دستیابی به هدف فوق‌الذکر توسعه می‌دهیم. ما آزمایش‌های عددی را با استفاده از داده‌های گشت به‌دست‌آمده از بازرسان شهری در ژنگژو، چین انجام می‌دهیم. به وضوح نشان دهد که الگوریتم پیشنهادی مسیرهای معقولی ایجاد می کند که میانگین زمان پاسخگویی به رویدادها و تعداد بازرسان گشت را کاهش می دهد. علاوه بر این، ما الگوریتم را برای سه سناریو زمانی مختلف (جاده‌هایی با میانگین تعداد رویدادهای مختلف) آزمایش می‌کنیم و کارایی الگوریتم را نشان می‌دهیم. نتایج تجربی نشان می‌دهد که الگوریتم پیشنهادی ما نسبت به سایر الگوریتم‌های موجود پایدارتر و کارآمدتر است.

کلید واژه ها:

بهینه سازی مسیریابی گشت ; مدیریت شهر هوشمند ؛ طبقه بندی بخش جاده ; الگوریتم ژنتیک

۱٫ مقدمه

در سال‌های اخیر، شهرهای هوشمند به یک منطقه تحقیقاتی تبدیل شده‌اند و به عنوان یک استراتژی برای بهبود کیفیت زندگی مورد استفاده قرار گرفته‌اند [ ۱ ، ۲ ، ۳ ]. مدیریت شهر هوشمند مدل جدیدی از مدیریت شهری است که در زمینه ساخت و ساز شهر هوشمند توسعه یافته است [ ۴ ، ۵ ، ۶ ، ۷ ]. مدل مدیریت شهر هوشمند وضعیت مدیریت را از نظر تقسیم بندی، تقاطع هوشمند، مدیریت گسترده، عدم نظارت و ناکارآمدی تغییر داده است [ ۸ ، ۹ ]. این مدل مدیریت شهری را از حالت مدیریت گسترده به حالت فشرده، دقیق و بلادرنگ تبدیل می کند.

با توسعه شهرنشینی در چین، دسترسی محدود به مشاغل شهری منجر به خوداشتغالی، از جمله عملیات غیرقانونی و راه اندازی دکه های کنار جاده ای شده است. این فعالیت ها چالش هایی را برای ساخت شهرهای هوشمند ایجاد می کند. دولت چین تیم های مجری قانون مدیریت شهری را برای نظارت بر ساخت شهر هوشمند می فرستد. تیم‌های مجری قانون مدیریت شهری از گشت‌ها برای تقویت مدیریت این فعالیت‌ها استفاده کرده‌اند که در نتیجه مجموعه‌ای از رویدادهای اجرای قانون مدیریت شهری رخ داده است [ ۱۰ ]. بازرسان اجرای مدیریت شهری شبیه به افسران پلیس محلی هستند که برای مشکلات در جاده ها گشت زنی می کنند.

برای مقابله سریع با رویدادهای اجرای قانون و تقویت تعمیر و نگهداری زیرساخت ها، بازرسان شهری می توانند به طور جامع در جاده ها گشت زنی کنند. یک مسیر گشت باید تمام گوشه های جاده را پوشش دهد و بر بخش های کلیدی تأکید کند. بسیار مهم است که مسیرهای گشت زنی مناسب برای بازرسان فراهم شود.

این مقاله بر روی مشکل مسیرهای گشت در مدیریت شهر هوشمند تمرکز دارد. مدلی پیشنهاد شده است که یک مسیر گشت را با به حداقل رساندن تعداد بازرسان شهری مورد نیاز و میانگین زمان پاسخگویی برای رویدادها بهینه می‌کند. سپس الگوریتمی برای حل مسئله تحقیق طراحی می شود. این الگوریتم بخش‌های مسیر گشت‌زنی را بر اساس فراوانی رویدادهای اجرای قانون شهری طبقه‌بندی می‌کند و عملگرهای متقاطع و جهش الگوریتم ژنتیک برای به دست آوردن یک راه‌حل بهینه بهبود می‌یابند.

ادامه مقاله به شرح زیر تدوین شده است. در بخش ۲ ، ادبیات مربوط به این مطالعه پژوهشی را مرور می کنیم. در بخش ۳ ، مسئله بهینه سازی گشت مدیران شهری در یک منطقه شبکه تشریح شده و یک مدل بهینه سازی مسیر گشت ایجاد شده است. ما یک الگوریتم موثر برای حل مسئله تحقیق بر اساس الگوریتم ژنتیک در بخش ۴ پیشنهاد می کنیم. در بخش ۵ ، ما محاسبات عددی و تجزیه و تحلیل را با در نظر گرفتن سناریوهای دنیای واقعی انجام می دهیم. ما نتیجه‌گیری می‌کنیم و جهت‌های تحقیقاتی آینده را در بخش ۶ پیشنهاد می‌کنیم.

۲٫ بررسی ادبیات

این بخش مرور ادبیات را شرح می‌دهد، از جمله فرآیندهای مدیریت شهر هوشمند، بهینه‌سازی مسیر در گشت‌ها و استفاده از الگوریتم‌های ژنتیک.

۲٫۱٫ برنامه ریزی گشت در مدیریت شهر هوشمند

IBM (شرکت ماشین‌های تجاری بین‌المللی) در ایالات متحده برای اولین بار در سال ۲۰۰۸ یک مفهوم مدیریت جدید برای شهرهای هوشمند پیشنهاد کرد [ ۱۱ ، ۱۲ ، ۱۳ ، ۱۴ ]. مدیریت شهر هوشمند استفاده از منابع اطلاعاتی شهر و فناوری ارتباطی برای تجزیه و تحلیل و پردازش رویدادها و اجزای یک شهر است [ ۲ ، ۳ ، ۱۵ ]. فناوری های اطلاعات و ارتباطات (ICT) دارای هوش مصنوعی و کلان داده ها به طور گسترده در چارچوب شهرهای هوشمند استفاده می شوند [ ۱۶ ].

مشکل زمانبندی گشت یک تقاطع بین ICT، انرژی و حمل و نقل است. این تخصیص پرسنل برای گشت زنی در شبکه حمل و نقل شهری است [ ۱۷ ]. اداره مدیریت شهر هوشمند تعدادی از بازرسان شهری را برای گشت زنی در شبکه ترافیک خیابانی به منظور حفاظت از اماکن عمومی برای حل برخی مشکلات شبکه خیابانی مانند ساخت و سازهای غیرقانونی و اشغال جاده ها مأمور می کند [ ۱۸ ، ۱۹ ].

۲٫۲٫ بهینه سازی مسیر در Street Patrol

در زندگی واقعی بسیاری از خدمات توزیع شده در خیابان وجود دارد. یک مسیر خوب طراحی شده می تواند هزینه یک سرویس توزیع شده را به میزان قابل توجهی کاهش دهد. بنابراین، مسائل بهینه‌سازی مسیریابی به طور فزاینده‌ای برای تحقیقات بنیادی و کاربردها مورد مطالعه قرار می‌گیرند [ ۱۹ ]. گشت خیابانی یک فعالیت ضروری است. افسران گشت زنی از موارد اضطراری جلوگیری می کنند و در مورد حوادث بلادرنگ اقدام می کنند [ ۲۰ ، ۲۱ ، ۲۲ ]. مسیرهای گشت زنی کارآمد با استفاده از سیستم های اطلاعات کامپیوتری و سیستم های اطلاعات جغرافیایی مقرون به صرفه تر (GIS) طراحی شده اند [ ۲۳ ].

بهینه سازی مسیر برای گشت خیابانی رایج است و تحقیقاتی نیز در مورد بهینه سازی مسیرهای گشت انجام شده است. افسران امنیت عمومی به منظور اطمینان از ایمنی و مبارزه با جرایم، گشت‌های روزانه خیابانی را انجام می‌دهند [ ۲۴ ]. هدف بهینه سازی گشت، تخصیص پرسنل و مسیر بود. چنگ و همکاران یک مدل تخصیص وظیفه گشت جاده ای بهینه شده و با کارایی بالا برای وسایل نقلیه هوایی بدون سرنشین (چند پهپاد) [ ۲۵ ] ایجاد کرد. طول مسیرهای گشت و تعداد پهپادها به حداقل رسیده است. فو و همکاران مشکل برنامه ریزی مسیر گشت امنیت جامعه هوشمند را حل کرد [ ۲۶]. یک چارچوب شبیه‌سازی گشت جامعه برای تعیین و تکامل مجموعه‌ای از مسیرها و یافتن راه‌حل بهینه استفاده می‌شود. مدل شبیه سازی چند عاملی برای تعیین محدودیت ها و یافتن مقدار هدف مسیر استفاده می شود. شیائو و همکاران بررسی پرسنل گشت و وسایل نقلیه در سیستم برق به منظور شناسایی مشکلات در شبکه توزیع [ ۲۷ ].

مطالعاتی وجود دارد که تاکید می‌کند گشت‌های خیابانی باید بر نقاط داغ متمرکز شوند و تأثیر موارد را در مسیرهای گشت زنی منعکس کنند. گشت زنی پلیس در مناطقی با کانون های جرم و جنایت بالا بر اساس تجزیه و تحلیل جرایم جغرافیایی [ ۲۸ ]. استقرار پلیس با مشخص کردن نقاط کانونی بهینه شده است [ ۲۲ ]. با این حال، مطالعات کمی وجود دارد که بر بهینه‌سازی مسیر گشت‌ها در نقاط داغ متمرکز باشد.

۲٫۳٫ کاربرد الگوریتم ژنتیک در مسئله مسیریابی خودرو

مسئله مسیریابی خودرو (VRP) برای اولین بار توسط Dantzig [ ۲۹ ] ارائه شد. مشکلات مسیریابی خودرو عمدتاً به‌عنوان VRP خازنی [ ۳۰ ، ۳۱ ، ۳۲ ، ۳۳ ]، VRP محدود به فاصله [ ۳۲ ، ۳۴ ، ۳۵ ، ۳۶ ]، VRP با پنجره زمانی [ ۳۵ ، ۳۷ ] و VRP با بک‌هال ، [۳۵، ۳۷] و VRP30 طبقه‌بندی می‌شوند . ۳۱ ، ۳۸ ].

در سال های اخیر تحقیقات زیادی در مورد VRP صورت گرفته است. VRP به منظور بهینه سازی منابع موجود مانند منابع انرژی سبز و حمل و نقل مانند توزیع بار استفاده می شود [ ۳۹ ، ۴۰ ]. لین و همکاران [ ۴۱ ] یک VRP را برای حل مشکل مسیریابی هزینه زمان و انرژی پیشنهاد کرد. موسولینو و همکاران [ ۴۲ ] مشکل VRP را در یک شبکه جاده شهری حل می کند. پولمنی و همکاران [ ۴۳ ] یک VRP در رابطه با حمل و نقل محصولات لبنی توسط خرده فروشان شهری ارائه کرد.

الگوریتم ژنتیک برای اولین بار توسط هالند در سال ۱۹۷۵ ارائه شد [ ۴۴ ، ۴۵ ]. این روش به طور گسترده برای حل مسائل مسیریابی عملی استفاده می شود. گشت خیابانی یک مشکل رایج مسیریابی وسایل نقلیه (VRP) است. جئون و همکاران یک الگوریتم ژنتیک ترکیبی جدید (HGA) برای حل ظرفیت VRP پیشنهاد کرد و تولید راه حل اولیه در الگوریتم ژنتیک بهبود یافته است [ ۴۶ ]. برگر و همکاران یک الگوریتم ژنتیک تطبیقی (AGA) را برای حل VRP با یک پنجره زمانی بررسی کرد [ ۴۷ ]]. این الگوریتم با اصلاح عملگرهای ژنتیکی باعث می شود که دو جمعیت به طور همزمان تکامل یابند. ژو و همکاران یک الگوریتم ژنتیک چند هدفه (MOGA) را با بهبود عملیات انتخاب و اپراتور متقاطع یک نقطه ای و عملگر جهش برای حل مشکل مسیریابی وسیله نقلیه [ ۴۸ ] ارائه کرد. با این حال، مطالعات کمی وجود دارد که بر روی عملگرهای متقاطع چند نقطه‌ای و عملگرهای جهش در الگوریتم ژنتیک تمرکز دارند.

کاستی‌های مطالعات قبلی به شرح زیر است: (۱) جمع‌آوری اطلاعات یک فرآیند مهم در مدیریت شهر هوشمند است، اما تحقیقاتی که بر گشت خیابانی در مورد بازرسان شهری متمرکز باشد، وجود ندارد، (۲) برای بهینه‌سازی مسیر در گشت خیابانی، مطالعات کمی مناطق داغ و رویدادهای فرکانس بالا را در نظر گرفته اند و (۳) الگوریتم های ژنتیک فقط عملگرهای متقاطع و جهش یک نقطه ای را در نظر می گیرند و فاقد عملگرهای متقاطع چند نقطه ای و عملگرهای جهش هستند.

۳٫ مشکل SPRP در مدیریت شهر هوشمند

این بخش مشکل مسیر گشت خیابانی (SPRP) را در مدیریت شهر هوشمند شرح می دهد. به طور خاص، شامل دو نکته است: (۱) تعریف خاص مسئله و (۲) تابع هدف و محدودیت های مدل.

۳٫۱٫ تعریف مشکل

مشکل مسیر گشت خیابانی (SPRP) در مدیریت شهر هوشمند را می توان به شرح زیر توصیف کرد: یک بخش مدیریت شهر هوشمند مناطق گشت را بر اساس منطقه اجرای قانون مدیریت شهری ایجاد می کند و افسران گشت شهری را برای گشت اعزام می کند. به بازرسان شهری هر روز بر اساس مسیری تعیین شده گشت تعیین می شود. بازرسان بین صبح و بعدازظهر تعویض می شوند و هر فرد شش ساعت در روز کار می کند. آنها در جاده های اصلی در امتداد شبکه راه ها گشت زنی می کنند. تعداد خودروهای موجود در بخش محدود است. گشت ها از مسیری از پیش تعریف شده حرکت می کنند.

مفروضات به شرح زیر است: (۱) یک بازرس شهری از یک نقطه شروع حرکت می کند، از هر مسیر عبور می کند و در نهایت به نقطه شروع باز می گردد، (۲) مسیرهای گشت بازرسان یک شبکه گشت را تشکیل می دهند. یک مسیر گشتی از چندین بخش جاده متصل تشکیل شده است. مسیر یک حلقه بسته است و (۳) بخش‌های جاده‌ای با وقوع جرم بالا دارای فرکانس گشت‌زنی افزایش یافته است.

در شرایط فرضی، یک نیروی انتظامی مدیریت شهری چندین بازرس شهری را برای گشت زنی در منطقه مربوطه اعزام می کند. هدف دستیابی به بهترین ترکیب از میانگین زمان واکنش به حادثه و تعداد بازرسان است. مدل شبکه گشت را می توان با نمودار شبکه ترافیک G = (X, E) نشان داد، که در آن X مجموعه ای از گره ها و E نشان دهنده لبه بازدید شده در شبکه است.

متغیرهای تصمیم باینری به صورت زیر تعریف می شوند:

ایکس ک من ج = {۱ i f i n s p e c t o r s p a t r o l f r o m s e g m e n t i t o j i n r o u t e k ۰ o t h e r w i s e

(۱)

تی ک من ج = {۱ i f i n s p e c t o r s p a t r o l f r o m s e g m e n t i t o j i n r o u t e k ۰ o t h e r w i s e

(۲)

جایی که $t_{i j}$ و $c_{i j}$ نشان دهنده مدت زمان سفر بازرسان از بخش i به j و مواردی است که در طول بخش رخ داده است $i$ به $j$ ، به ترتیب.

۳٫۲٫ تابع هدف

جدول ۱ فهرستی از نمادهای ریاضی استفاده شده در مدل SPRP را نشان می دهد.

توابع هدف روی مسئله به صورت زیر آورده شده است:

m i n Z = α اف ۱ + β اف ۲

(۳)

α + β = ۱

(۴)

اف ۱ = \sum من \in E آ من ۲ ( \sum r \sum j \in E ایکس ک من ج \sum من j \in E تی من ج ایکس ک من ج / L ک )

(۵)

اف ۲ = ک n

(۶)

تابع هدف (۳) ترکیبی از F _۱ و F _۲ است که دو تابع هدف هستند که برای به حداقل رساندن میانگین زمان پاسخ حادثه [ ۴۹ ] و تعداد بازرسان گشت استفاده می شوند. این تابع هدف (۴) دارای دو بعد است: وزن ها

α

β

برای میانگین زمان واکنش به حادثه و تعداد بازرسان. هدف کلی ۱ است.

۳٫۳٫ محدودیت ها

محدودیت های مشکل به صورت زیر ارائه شده است:

\sum v ک \leq V

(۷)

\sum (من ، ج) \in E ایکس ک من ج = \sum (j, i) \in E ایکس ک j i من \neq j

(۸)

\sum (i, ۱) \in E ایکس ک من ۱ = ایکس ۰

(۹)

\sum (۱, i) \in E ایکس ک ۱ i = ایکس ۰

(۱۰)

\sum k \in K ایکس ک من ج \geq ۱ i \neq j

(۱۱)

\sum (i, j) \in E ایکس ک من ج = \sum (j, l) ایکس ک j l i \neq j ، j \neq l

(۱۲)

محدودیت (۷) تضمین می کند که تعداد وسایل نقلیه در حال گشت از تعداد کل وسایل نقلیه در بخش تجاوز نمی کند. معادله (۸) محدودیت‌هایی را برای تعداد ورودی‌ها و خروجی‌های هر بخش ارائه می‌کند. محدودیت های (۹) و (۱۰) تضمین می کند که گشت از نقطه x _۰ شروع می شود و در نهایت به نقطه باز می گردد . محدودیت (۱۱) نشان دهنده عبور از هر بخش حداقل یک بار، و محدودیت (۱۲) نشان دهنده یک بازرس از ورود به گره j و خروج از گره l است.

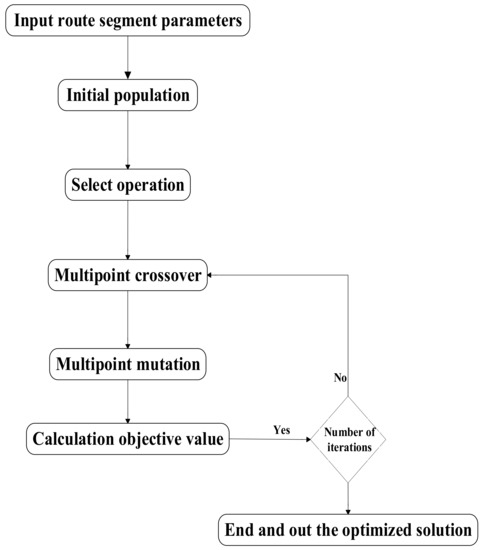
۴٫ الگوریتم پیشنهادی برای SPRP

در این بخش از ویژگی‌های مدل ایجاد شده برای پیشنهاد گشت‌زنی اولویت‌دار و الگوریتم ژنتیک چندهدفه (DP-MOGA) برای بازرسان شهری استفاده می‌شود و با استفاده از مراحل زیر راه‌حل بهینه برای وظیفه گشت به دست می‌آید.

ابتدا، محدودیت‌ها برای تعیین اهمیت نسبی بخش‌های جاده پردازش می‌شوند. دوم، اهمیت نسبی بخش ها بسته به فراوانی موارد تعیین می شود. سپس بخش‌های جاده‌ای گشتی طبقه‌بندی می‌شوند. سوم، یک الگوریتم ژنتیک بهبود یافته برای ایجاد مسیر گشت بهینه استفاده می شود.

۴٫۱٫ الگوریتم طبقه بندی بخش گشت

الگوریتم طبقه بندی بخش های گشت را بر اساس درجه اهمیت آنها دسته بندی می کند. بنابراین بخش های گشت به مناطق کلیدی و مناطق معمولی تقسیم می شوند. بخش های کلیدی نیاز به افزایش تعداد و دفعات گشت زنی دارند. الگوریتم بر اساس تعداد حوادث و زمان گشت برای هر بخش جاده است.

در این بخش، بخش‌های جاده را طبقه‌بندی می‌کنیم، تعداد گشت‌ها را برای بخش‌های کلیدی جاده افزایش می‌دهیم و داده‌هایی را برای مسیر شبکه، از جمله تعداد بخش‌های مسیر، زمان گشت و پارامترهای اولیه برای حوادثی که در طول بخش‌ها رخ می‌دهند، به‌دست می‌آوریم. سپس، برای هر بخش جاده از $K_{1}$ به $K_{i}$ ، زمان گشت و نسبت حوادث را به تعداد کل حوادث تعیین می کنیم که برای تعیین آستانه اهمیت یک بخش جاده استفاده می شود. در نهایت، نسبت مسیر را با آستانه تنظیم شده مقایسه می کنیم. اگر نسبت مسیر بیشتر از آستانه باشد، بخش جاده یک بخش گشت کلیدی است و تعداد گشت‌ها در بخش کلیدی جاده افزایش می‌یابد. اگر نسبت مسیر کمتر از آستانه باشد، بخش جاده یک بخش مسیر عادی در نظر گرفته می شود و تعداد عادی گشت به بخش جاده اختصاص می یابد. مراحل خاص در الگوریتم ۱ توضیح داده شده است.

الگوریتم ۱: الگوریتم طبقه بندی مسیر گشت

۱: ورودی :

k_{1}

\leftarrow

تعداد گشت ها برای بخش i.

M a x_{k} \leftarrow

حداکثر تعداد قطعه جاده؛

t_{i} \leftarrow

زمان گشت برای بخش جاده i;

c_{i} \leftarrow

تعداد حوادث رخ داده در بخش جاده i;

M a x_{t_{i}}

Max_ti←حداکثر زمان گشت برای بخش جاده i;

M i n_{t_{i}} \leftarrow

حداقل زمان گشت برای بخش جاده i;

M a x_{c_{i}} \leftarrow

حداکثر تعداد حوادث رخ داده در جاده i.

M i n_{c_{i}} \leftarrow

حداقل تعداد حوادث رخ داده در بخش جاده i.

n_{k} \leftarrow

تعداد گشت‌ها برای بخش‌های جاده‌ای معمولی؛
k←تعداد گشت‌های اضافی برای بخش‌های کلیدی؛
۲: تکرار:
۳:

M a x_{k} \leftarrow

آخرین بخش؛
۴: اگر

K_{i} \leq M a x_{k}

، سپس

k_{i} = k_{i} + 1

۵: برای هر داده از بخش گشت ۶: اگر
$c_{i} \geq a (\frac{M a x_{c_{i}}}{M i n_{t_{i}}} - \frac{M i n_{c_{i}}}{M a x_{c_{i}}})$ سپس
۷: این بخش را به عنوان بخش گشت زنی کلیدی مسیر
۸ تنظیم کنید:

n_{k} = n_{k} + k

;
۹: else
۱۰: این بخش را به عنوان یک مسیر معمولی بخش گشت تنظیم کنید.
۱۱: پایان اگر
۱۲: پایان برای
۱۳: پایان اگر
۱۴: تا $K_{i} \geq M a x_{K}$ ;

۴٫۲٫ الگوریتم ژنتیک

الگوریتم ژنتیک شامل رمزگذاری کروموزوم، مقداردهی اولیه جمعیت، رمزگشایی، اجرای تابع تناسب، انتخاب، متقاطع، جهش و جایگزینی است [ ۵۰ ]. لازم است تعدادی تکرار طراحی شود که اندازه جمعیت تکرار، احتمال متقاطع و احتمال جهش را تغییر دهد. نتایج نهایی متفاوتی با استفاده از پارامترهای مختلف تولید می شود.

در این بخش، ما یک الگوریتم ژنتیک بهبود یافته را طراحی می کنیم تا از حل هموار مشکلات گشت زنی برای دولت های شهرهای هوشمند اطمینان حاصل کنیم. الگوریتم طراحی شده به یک استراتژی نخبه گرایانه [ ۵۱ ] اضافه می شود. پس از هر فرآیند عملیات، مقدار تابع هدف برای داده های ذخیره شده محاسبه شده و برای انتخاب نتیجه بهینه استفاده می شود. این روش تنوع جمعیت اولیه را حفظ می کند و از همگرایی زودرس تابع هدف جلوگیری می کند. این الگوریتم کارایی فرآیند جستجو را بهبود می بخشد. نمودار جریانی از الگوریتم ژنتیک بهبود یافته در شکل ۱ نشان داده شده است .

۴٫۲٫۱٫ طرح رمزگذاری

کدگذاری کروموزوم مبنایی برای عملیات بعدی متقاطع و جهش است. ماتریس یک کروموزوم است که در آن تعداد ردیف ها تعداد مسیرها و ستون ها نشان دهنده بخش های جاده در هر مسیر است. کد مسیر یک عدد صحیح از ۱ تا K است و i نشان دهنده یک بخش جاده است. ترکیبی از کدگذاری عدد صحیح و ماتریس در الگوریتم استفاده شده است.

۴٫۲٫۲٫ عملیات متقاطع

عملیات متقاطع الگوریتم ژنتیک شامل انتخاب یک طرح برنامه ریزی مسیر برای دو والدین و تعیین تعداد مسیرهایی است که باید مبادله شوند. برای اطمینان از اتصال مسیر گشت زنی، با تبادل تصادفی موقعیت مسیر، یک اپراتور متقاطع طراحی می کنیم. روش تقاطع چند نقطه ای برای افزودن و حذف نقاط مسیر گشت برای اتصال چندین مسیر اتخاذ شده است.

روش دقیق در الگوریتم ۲ ارائه شده است.

الگوریتم ۲: اپراتور متقاطع

۱: ورودی: والد ۱←مسیر ۱ انتخاب شده از جمعیت.
والدین ۲←مسیر ۲ متفاوت از والدین ۱ انتخاب شده از جمعیت.

a_{n} \leftarrow

یک بخش جاده انتخاب شده از مسیر ۱٫

b_{n} \leftarrow

یک بخش جاده انتخاب شده از مسیر ۲٫
۲: والد ۱ و والد ۲ را از جمعیت انتخاب کنید.
۳: بخش را انتخاب کنید

a_{n}

از والد ۱ و مسیر

b_{n}

از والدین ۲;
۴: انتخاب نقاط تقاطع در کروموزوم ها.
۵: بخش an و segment را مبادله کنید

b_{n}

در والد ۱ و والد ۲;
۶: پس از انجام مبادله، قطعه an1 و قطعه bn1 تولید کنید.
۷: برای مقایسه بین مسیر مبادله شده و مسیر اصلی ۸ را انجام دهید
: برای بخش گم شده ۹ را انجام دهید
: اگر بخش های جاده در طول مسیر به هم متصل هستند، ۱۰
: بخش های گم شده را اضافه کنید.
۱۱: else پس از تقسیم مسیر به بخش های متصل، بخش های گم شده را اضافه کنید.
۱۲: پایان اگر
۱۳: برای قطعه زائد ۱۴ را انجام دهید
: اگر قطعه در یک نقطه غیرتغییر ظاهر شود، سپس
۱۵: بخش های اضافی جاده را در نقطه غیرتبادل حذف کنید.
۱۶:   پایان اگر
۱۷:   پایان برای
۱۸: پایان برای
۱۹:   پایان برای
۲۰: مسیر تست عقلانیت داخلی.
۲۱: مسیر اصلی را با

a_{n_{1}}

b_{n_{2}}

;
۲۲: به روز رسانی والدین ۱ و والدین ۲٫

۴٫۲٫۳٫ عملیات جهش

ما یک طرح برنامه ریزی مسیر والد را که می تواند یک جهش چندبخشی باشد، برای عملیات جهش انتخاب می کنیم. در این بخش، یک روش جهش چند نقطه ای ارائه شده است که شامل انتخاب تصادفی نقاط جهش است.

فرآیند جهش در اینجا توضیح داده شده است. یک مسیر به طور تصادفی از طرح برنامه ریزی مسیر انتخاب می شود و سپس یک بخش جاده به طور تصادفی انتخاب می شود. بخش جاده ای که حذف شده است به طور تصادفی با سایر بخش های جاده ترکیب می شود. ما مقدار تابع هدف را برای طرح‌های برنامه‌ریزی مسیر مختلف محاسبه می‌کنیم، استراتژی نخبگان را اتخاذ می‌کنیم و تابع تناسب بهینه را انتخاب می‌کنیم. تابع هدف در این بخش به عنوان تابع تناسب تعریف شده است.

روش دقیق در الگوریتم ۳ ارائه شده است.

الگوریتم ۳: عملگر جهش

۱: ورودی: راه حل←مسیر ۳ در جمعیت پس از عملیات متقاطع.

c_{n}

←بخش جاده انتخاب شده از مسیر ۳٫
نقاط جهش←نقاط جهش در کروموزوم ها را انتخاب کنید.

f (t)

←عملکرد تناسب اندام؛
۲: بخش های جاده را از کروموزوم ها به عنوان بخش های مختلف جاده انتخاب کنید.
۳: یک بخش جاده را انتخاب کنید

c_{n}

از بخش های جاده به بهره برداری;
۴: یک نقطه جهش در کروموزوم را انتخاب کنید.
۵: بخش جاده را استخراج کنید

c_{n}

و این بخش را با سایر بخش های جاده ترکیب کنید.
۶: تکرار
۷: برای

c_{n} \leftarrow n

8 را انجام دهید
: تابع تناسب اندام را تحت برنامه های مسیر مختلف محاسبه کنید.
۹: کروموزوم های جهش یافته را بر اساس مقدار تابع تناسب مرتب کنید

f (t)

;
۱۰: ترکیب بخش جاده را با حداکثر مقدار انتخاب کنید

f (t)

;
۱۱: تست عقلانیت داخلی مسیر را انجام دهید.
۱۲: نقطه جهش را به روز کنید.
۱۳: به روز رسانی جمعیت;

۵٫ نتایج تجربی و تجزیه و تحلیل

در این بخش، شبکه واقعی راه برای شبیه سازی انتخاب شده و نتایج تجربی مورد تجزیه و تحلیل قرار می گیرد. در ابتدا، ما یک بخش از یک شبکه جاده واقعی را برای ایجاد سه سناریو مختلف مدل می‌کنیم. در مرحله دوم، الگوریتم در سه سناریو ارزیابی می شود. در نهایت، الگوریتم پیشنهادی در این مقاله با سایر الگوریتم‌ها مقایسه و تحلیل می‌شود.

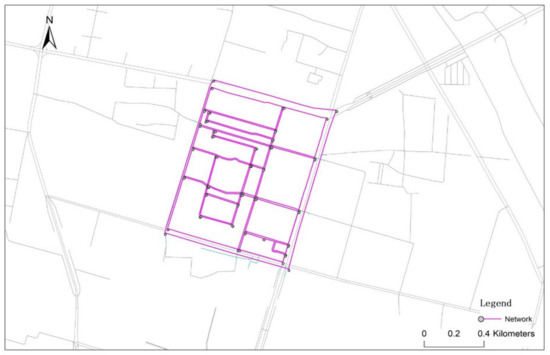
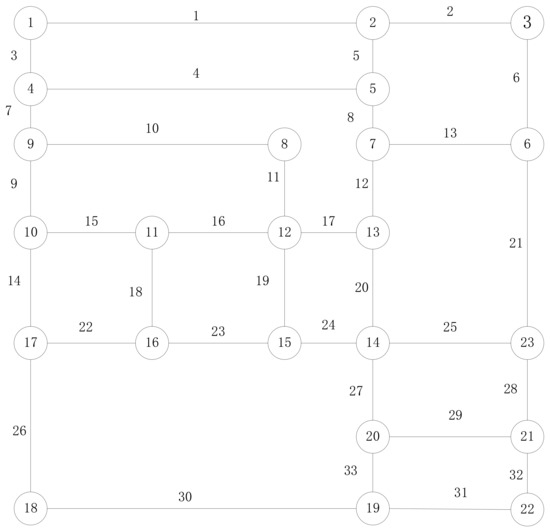
۵٫۱٫ داده ها و پارامترها

ژنگژو یک شهر استانی در هنان چین است. این شهر در مرکز چین واقع شده است و یک شهر مدرن جدید است. یک شبکه واقعی از منطقه ای در ژنگژو در این بخش در نظر گرفته شده است. الگوریتم پیشنهادی در MATLAB 2018a کدگذاری شده است و آزمایش‌ها بر روی رایانه‌ای با پردازنده Core i7 اینتل (۳٫۷ گیگاهرتز) و ۸ گیگابایت رم انجام می‌شود.

منطقه مورد بررسی در این مطالعه در شکل ۱ نشان داده شده است . مدل شبکه راه برای منطقه ارکی، ژنگژو است. چندین مدیر در منطقه شبکه مشخص شده گشت می زنند. هر مدیر شهری دارای یک مسیر گشت ثابت متشکل از بخش های جاده است. فرض بر این است که این شبکه جاده ای توسط چندین مدیر با دوچرخه های برقی گشت زنی می شود. شبکه راه برای منطقه مورد مطالعه در شکل ۲ نشان داده شده است . شکل بخشی از شبکه جاده ای نزدیک جاده ژیژان در ناحیه ارقی را نشان می دهد. یک مدل شبکه راه برای جاده ها در منطقه گشت روی نقشه ایجاد شده است. عرض جاده با توجه به وضعیت واقعی در شکل نشان داده شده است. شکل ۳یک مدل انتزاعی ریاضی از مدل شبکه جاده‌ای است که می‌توان آن را به صورت یک نمودار بدون جهت انتزاع کرد. این شبکه شامل ۲۳ گره و ۶۶ قطعه جاده هدایت شده است.

۵٫۲٫ ارزیابی الگوریتم

بازرسان شهری در سه بازه زمانی مختلف صبح، ظهر و عصر گشت‌زنی می‌کنند. از آنجایی که فراوانی موارد برای سه دوره زمانی متفاوت است، بازرسان گشت در هر دوره بر بخش‌های مختلف جاده تمرکز می‌کنند. دو پارامتر اصلی برای بخش‌ها وجود دارد: زمان سفر و میانگین تعداد رویدادها. هر چه زمان رانندگی کوتاهتر باشد، بخش جاده هموارتر می شود. هر چه زمان رانندگی کوتاهتر باشد، بخش جاده هموارتر می شود. هر چه زمان رانندگی طولانی تر باشد، بخش جاده شلوغ تر است. با توجه به پارامترهای فوق، سه سناریو زمانی مختلف پیشنهاد شده است.

سناریو ۱: میانگین تعداد رویدادها برای بخش‌های خاص جاده وجود دارد و وضعیت جاده در کل شبکه نامتعادل است. گشت‌ها باید روی این بخش‌های جاده‌ای با وقوع زیاد تمرکز کنند.

سناریو ۲: زمان سفر و میانگین تعداد حوادث برای همه بخش‌های جاده مشابه است و تفاوت عمده‌ای بین بخش‌های جاده وجود ندارد. وضعیت جاده کل شبکه متعادل است.

سناریو ۳: برخی از بخش‌های جاده زمان رانندگی طولانی‌تری دارند و وضعیت جاده در کل شبکه نامتعادل است.

این سه سناریو منعکس کننده موقعیت های گشت زنی واقعی هستند. ما با استفاده از این سناریوها تحلیل های مختلفی را انجام می دهیم.

تجزیه و تحلیل نتایج آزمون با استفاده از آمار ریاضی و شناسایی میزان تأثیر عوامل مختلف بر نتایج مفید است. برای ارزیابی کارایی الگوریتم از واریانس استفاده می کنیم.

ما کیفیت یک راه حل را با استفاده از D مختلف ارزیابی می کنیم که به صورت زیر تعریف می شود:

D = \sum n i = ۱ ( ایکس من - ایکس ¯ ) ۲ n ————-⎷

(۱۳)

جایی که $x_{i}$ تعداد بخش‌های یک مسیر، n تعداد کل مسیرها و $\bar{x}$ میانگین تعداد قطعات جاده است. راه حل تولید شده توسط الگوریتم گشت بر اساس مناطق کلیدی برای تعیین واریانس استفاده می شود. الگوریتمی با مقدار D کمتر کارآمدتر است.

برای ارزیابی عملکرد الگوریتم می توان از شکاف کران پایین (LBG) استفاده کرد که به صورت زیر تعریف می شود:

LBG = L m a x ( R ) - L m i n ( R ) L m a x ( R )

(۱۴)

جایی که $L_{m a x} (R)$ طول طولانی ترین بخش جاده است و $L_{m i n} (R)$ طول کوتاه ترین بخش جاده است. الگوریتمی با مقدار LBG بالاتر کارآمدتر است. جدول ۲ مقدار هدف، D و LBG را در سه سناریوی مختلف نشان می دهد. مقادیر الگوریتم در سه سناریو تغییر چندانی نمی کند. نتایج نشان می‌دهد که الگوریتم DP-MOGA عملکرد پایداری دارد.

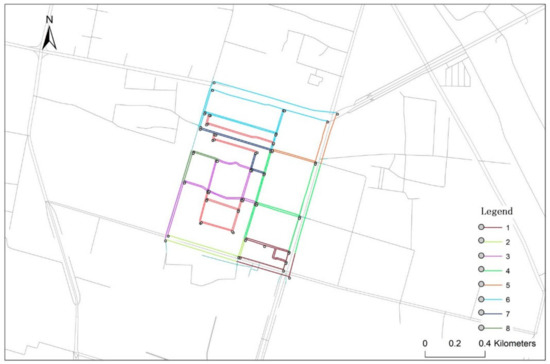
۵٫۳٫ تحلیل مقایسه ای

الگوریتم ژنتیک چند هدفه (MOGA) برای حل مسائل بهینه سازی چند هدفه با بهبود الگوریتم های ژنتیک استفاده می شود [ ۵۲ ]. ما از گشت زنی اولویت و الگوریتم ژنتیک چند هدفه (DP-MOGA) در مقایسه با MOGA و الگوریتم جستجوی محله در مقیاس بسیار بزرگ (VLNS) استفاده می کنیم [ ۴۹ ].

نتایج به دست آمده در جدول ۳ نشان داده شده است. مقدار هدف، زمان پاسخ رویداد و همگرایی در DP-MOGA کوچکترین مقادیر هستند. نتایج نشان می‌دهد که الگوریتم DP-MOGA مؤثرتر از الگوریتم‌های MOGA و VLNS است.

در زندگی واقعی، بر اساس سناریوی ۱، یک بخش مدیریت شهر هوشمند به بازرسان شهری وظایف گشت را محول می‌کند. بازرسان شهری مسیرهایی را برای گشت‌ها بر اساس تجربه واقعی طراحی می‌کنند. شکل ۴ طرح گشت مسیر را برای سناریوی واقعی نشان می دهد.

الگوریتم پیشنهادی تعداد گشت‌ها را بر اساس فراوانی بالای رویدادها در بخش‌ها افزایش می‌دهد. بهبود عملگر متقاطع و اپراتور جهش الگوریتم ژنتیک منجر به کوتاه‌ترین میانگین زمان پاسخگویی به حوادث و کمترین بازرسان گشت می‌شود. الگوریتم پیشنهادی برای بهینه سازی مسیر برای منطقه مورد مطالعه استفاده می شود.

جدول ۴ تعداد حوادث شبکه جاده ای و زمان گشت جاده ای را در سناریوی واقعی نشان می دهد. جدول ۵ طرح گشت زنی مسیر را بر اساس تجربه واقعی نشان می دهد. طرح گشت مسیر بهینه شده در جدول ۶ نشان داده شده است . مسیرهای گشت زنی واقعی قبل و بعد از بهینه سازی در شکل ۴ و شکل ۵ نشان داده شده است.

جدول ۷ نشان می دهد که مقدار تابع هدف طرح بهینه شده ۰٫۵۱۱۲ است، در مقایسه با مقدار ۰٫۵۱۵۹ برای طرح بهینه نشده. در مقایسه با مسیر گشت زنی موجود برای بازرسان شهری، طرح گشت مسیر بهینه شده میانگین زمان پاسخگویی و تعداد پرسنل را برای موارد واقعی کاهش می دهد. استفاده از این روش بهینه سازی برای گشت های روزانه واقعی می تواند کارایی گشت ها را بهبود بخشد. این روش باعث می شود تا بازرسان شهری ترتیب داده شوند و رویدادهای مجری قانون شهری بهتر رسیدگی شود.

۶٫ نتیجه گیری و کار آینده

در این مطالعه مدلی برای گشت خیابانی توسط بازرسان شهری پیشنهاد می شود. تعداد بازرسان مستقر برای گشت اختصاص داده شده است و مسیر گشت بهینه شده است. هدف به حداقل رساندن میانگین زمان پاسخگویی و تعداد بازرسان است. سپس، ما یک گشت اولویت و الگوریتم ژنتیک چند هدفه (DP-MOGA) را برای حل مسئله بهینه‌سازی پیشنهاد می‌کنیم. الگوریتم پیشنهادی فرکانس و تعداد گشت‌ها را در نواحی کلیدی با بروز بالای حوادث افزایش می‌دهد. ما عملگر متقاطع و عملگر جهش الگوریتم ژنتیک را بهبود می‌بخشیم. یک استراتژی انتخاب نخبگان برای حفظ تنوع جمعیت و جلوگیری از همگرایی زودرس اضافه شده است. در نهایت، یک سری آزمایش با استفاده از یک مطالعه موردی در ژنگژو، چین انجام شد. هدف به حداقل رساندن میانگین کلی زمان پاسخ به حادثه و تعداد پرسنل گشت است. الگوریتم پیشنهادی برای سناریوهای واقعی اعمال می شود.

سه سناریو (S1، S2 و S3) برای تحلیل مدل این مقاله تعریف شده‌اند. سناریوها بر اساس زمان سفر و میانگین تعداد رویدادها در بخش های جاده طبقه بندی می شوند. از طریق تجزیه و تحلیل تجربی می توان به نتایج زیر دست یافت:

ارزیابی الگوریتم از طریق محاسبه مقادیر واریانس نشان می‌دهد که DP-MOGA در سه سناریو عملکرد پایداری دارد.
الگوریتم DP-MOGA بهتر از الگوریتم MOGA و الگوریتم VLNS عمل می کند.
در زندگی واقعی، مدل پیشنهادی در این مقاله تخصیص پرسنل و مسیرهای گشت بازرسان شهری را بهینه می‌کند. این مدل کارایی گشت زنی را برای بازرسان بهبود می بخشد.

علاوه بر این، مدل ما کاربرد گسترده ای برای مدیریت شهر هوشمند دارد. مطالعات آینده تحقیقاتی ما بر جنبه هایی متمرکز خواهد بود که در این مطالعه در نظر گرفته نشده است: الگوریتم می تواند بسیاری از عوامل تأثیرگذار مانند مدت زمان رویدادهای تصادفی و سایر مشخصات آماری جاده و تغییرات زمانی در فرکانس شهر را در نظر بگیرد. حوادث مدیریتی و تغییرات پویا در مسیر گشت زنی خودروهای گشت. ما می توانیم مسیرهای گشت پویا را بر اساس ویژگی های زمانی و مسیر حرکت وسایل نقلیه گشت طراحی کنیم. در مطالعات آتی، این عوامل برای کاربردی‌تر کردن مسئله تحقیق مورد توجه قرار خواهند گرفت.

منابع

دامری، ر.پ. Cocchia، A. شهر هوشمند و شهر دیجیتال: بیست سال تکامل اصطلاحات. در مجموعه مقالات کنفرانس X فصل ایتالیایی AIS، ITAIS، میلان، ایتالیا، ۱۴ دسامبر ۲۰۱۳; صص ۱-۸٫ [ Google Scholar ]
هال، RE; باورمن، بی. براورمن، جی. تیلور، جی. تودوسو، اچ. Von Wimmersperg، U. چشم انداز یک شهر هوشمند . آزمایشگاه ملی بروکهاون: آپتون، نیویورک، ایالات متحده آمریکا، ۲۰۰۰٫ [ Google Scholar ]
سو، ک. لی، جی. فو، اچ. شهر هوشمند و برنامه های کاربردی. در مجموعه مقالات کنفرانس بین المللی ۲۰۱۱ در الکترونیک، ارتباطات و کنترل (ICECC)، نینگبو، چین، ۹ تا ۱۱ سپتامبر ۲۰۱۱٫ ص ۱۰۲۸-۱۰۳۱٫ [ Google Scholar ]
کاراگلیو، ا. دل بو، سی. Nijkamp، P. شهرهای هوشمند در اروپا. J. فناوری شهری. ۲۰۱۱ ، ۱۸ ، ۶۵-۸۲٫ [ Google Scholar ] [ CrossRef ]
چورابی، ح. نام، تی. واکر، اس. گیل-گارسیا، جی آر. ملولی، س. ناهون، ک. پاردو، TA; Scholl, HJ درک شهرهای هوشمند: یک چارچوب یکپارچه. در مجموعه مقالات چهل و پنجمین کنفرانس بین المللی هاوایی در علوم سیستمی در سال ۲۰۱۲، مائوئی، HI، ایالات متحده آمریکا، ۴ تا ۷ ژانویه ۲۰۱۲٫ صص ۲۲۸۹-۲۲۹۷٫ [ Google Scholar ]
لی، ی. لی، ی. Li, J. یک برنامه کاربردی و سیستم مدیریت شهر هوشمند. در مجموعه مقالات کنفرانس بین المللی انفورماتیک صنعتی و مهندسی کامپیوتر، شانشی، چین، ۱۰–۱۱ ژانویه ۲۰۱۵٫ صفحات ۱۶۲۶-۱۶۳۰٫ [ Google Scholar ]
رپتی، ا. مدل مجموعه شاخص های رابطه ای برای برنامه ریزی و مدیریت کاربری زمین شهری: رویکرد و کاربرد روش شناختی در دو مطالعه موردی. Landsc. طرح شهری. ۲۰۰۶ ، ۷۷ ، ۱۹۶-۲۱۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بارلتا، VS; کایوانو، دی. دیمارو، جی. Nannavecchia، A.; Scalera، M. مدیریت یک مدل یکپارچه شهر هوشمند از طریق مدیریت برنامه هوشمند. Appl. علمی ۲۰۲۰ ، ۱۰ ، ۷۱۴٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
پترولو، آر. لوسکری، وی. میتون، ن. به سوی یک شهر هوشمند مبتنی بر ابر چیزها، نظرسنجی در مورد چشم انداز و پارادایم های شهر هوشمند. ترانس. ظهور. مخابرات تکنولوژی ۲۰۱۷ ، ۲۸ ، e2931. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لیو، ی. ژان، ز. زو، دی. چای، ی. Xiujun، MA; Lun، WU ترکیب چند منبع داده های جغرافیایی بزرگ برای حس الگوهای ناهمگونی فضایی در یک فضای شهری. Geomat. Inf. علمی دانشگاه ووهان ۲۰۱۸ ، ۴۳ ، ۳۲۷-۳۳۵٫ [ Google Scholar ] [ CrossRef ]
کامرو، آ. آلبا، ای. شهر هوشمند و فناوری اطلاعات: بررسی. شهرها ۲۰۱۹ ، ۹۳ ، ۸۴–۹۴٫ [ Google Scholar ] [ CrossRef ]
ارمی، م. توما، ال. Sanduleac, M. مفهوم شهر هوشمند در قرن بیست و یکم. Procedia Eng. ۲۰۱۷ ، ۱۸۱ ، ۱۲-۱۹٫ [ Google Scholar ] [ CrossRef ]
هاشم، IAT; چانگ، وی. Anuar، NB; آدوول، ک. یعقوب، ط. گانی، ع. احمد، ای. Chiroma، H. نقش داده های بزرگ در شهر هوشمند. بین المللی J. Inf. مدیریت ۲۰۱۶ ، ۳۶ ، ۷۴۸-۷۵۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
زوبیزارتا، آی. سراوالی، ع. Arrizabalaga، S. مفهوم شهر هوشمند: چیست و چه باید باشد. ج. طرح شهری. توسعه دهنده ۲۰۱۶ , ۱۴۲ , ۰۴۰۱۵۰۰۵٫ [ Google Scholar ] [ CrossRef ]
هائو، ال. لی، ایکس. یان، ز. ChunLi، Y. تحقیق کاربردی و پیاده سازی شهر هوشمند در چین. در مجموعه مقالات کنفرانس بین المللی علوم و مهندسی سیستم ۲۰۱۲ (ICSSE)، دالیان، چین، ۳۰ ژوئن تا ۲ ژوئیه ۲۰۱۲٫ صص ۲۸۸-۲۹۲٫ [ Google Scholar ]
Jun, W. تحقیق در مورد چارچوب سیستم عامل شهر هوشمند بر اساس فناوری اطلاعات و ارتباطات جدید. صبح. جی آرتیف. هوشمند ۲۰۲۰ ، ۴ ، ۳۶-۴۱٫ [ Google Scholar ] [ CrossRef ]
لاو، HC; Gunawan، A. مسئله زمانبندی گشت. در مجموعه مقالات کنفرانس بین‌المللی روی تمرین و تئوری زمان‌بندی خودکار (PATAT)، پسر، نروژ، ۲۹ تا ۳۱ اوت ۲۰۱۲٫ [ Google Scholar ]
جو، EE پلیس شهر هوشمند. بین المللی J. Law Context ۲۰۱۹ ، ۱۵ ، ۱۷۷-۱۸۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ahr, D. کمک به مشکلات چند پستچی. دکتری پایان نامه، دانشگاه هایدلبرگ، هایدلبرگ، آلمان، ۲۰۰۴٫ [ Google Scholar ]
دیوینتر، م. وندویور، سی. واندر بکن، تی. ویتلوکس، اف. تحلیل مشکل مسیریابی گشت پلیس: بررسی. ISPRS Int. J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۱۵۷٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
واین، ن. آریل، ب. ردیابی گشت پلیس. سیاسی J. سیاست عمل. ۲۰۱۴ ، ۸ ، ۲۷۴-۲۸۳٫ [ Google Scholar ] [ CrossRef ]
Chainey، SP; ماتیاس، جی. Nunes Junior، FCF; کوئیلو داسیلوا، TL; de Macêdo، JAF; Magalhães، RP; د کی روش نتو، جی اف. سیلوا، دبلیو. بهبود ایجاد مسیرهای گشت پلیس نقطه داغ: مقایسه عملکرد اکتشافی شناختی با رویکرد محاسبات فضایی خودکار. ISPRS Int. J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۵۶۰٫ [ Google Scholar ] [ CrossRef ]
آنسلین، ال. گریفیث، ای. تیتا، جی. نقشه برداری جرم و تجزیه و تحلیل نقطه داغ. در جرم شناسی محیطی و تحلیل جرم ; ویلان: ابینگدون، بریتانیا، ۲۰۱۳; صص ۱۱۹-۱۳۸٫ [ Google Scholar ]
کالوو، اچ. گودوی- کالدرون، اس. مورنو-آرمنداریز، MA; بهینه سازی مسیرهای گشت زنی مارتینز-هرناندز، VM با استفاده از کلونی مورچه ها. در مجموعه مقالات کنفرانس مکزیک در مورد شناسایی الگوها، مکزیکو سیتی، مکزیک، ۲۴-۲۷ ژوئن ۲۰۱۵٫ صص ۳۰۲-۳۱۲٫ [ Google Scholar ]
چنگ، ال. ژونگ، ال. تیان، اس. Xing, J. الگوریتم تعیین تکلیف برای گشت جاده ای توسط پهپادهای متعدد با پایه های متعدد و استقامت قابل شارژ. دسترسی IEEE ۲۰۱۹ ، ۷ ، ۱۴۴۳۸۱–۱۴۴۳۹۷٫ [ Google Scholar ] [ CrossRef ]
فو، ی. زنگ، ی. وانگ، دی. ژانگ، اچ. گائو، ی. لیو، ی. تحقیق در مورد بهینه سازی مسیر بر اساس الگوریتم چند عاملی و ژنتیک برای گشت جامعه. در مجموعه مقالات کنفرانس بین المللی ۲۰۲۰ در علوم مهندسی و مدیریت شهری (ICUEMS)، زوهای، چین، ۲۴-۲۶ آوریل ۲۰۲۰؛ صص ۱۱۲-۱۱۶٫ [ Google Scholar ]
شن، ایکس. سانگ، ج. سان، ی. لیو، آر. کاربرد الگوریتم کلنی مورچه بهبود یافته در برنامه ریزی مسیر گشت زنی شبکه توزیع. در مجموعه مقالات هفتمین کنفرانس بین المللی IEEE 2016 در زمینه مهندسی نرم افزار و علوم خدمات (ICSESS)، پکن، چین، ۲۶ تا ۲۸ اوت ۲۰۱۶؛ صص ۵۶۰-۵۶۳٫ [ Google Scholar ]
ایلجازی، وی. میلیچ، ن. میلیدراگوویچ، دی. پوپوویچ، ب. ارزیابی ادراک افسران پلیس از نقاط داغ: برای بهبود آگاهی موقعیتی افسر چه کاری می توان انجام داد؟ ISPRS Int. J. Geo-Inf. ۲۰۱۹ ، ۸ ، ۲۶۰٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Dantzig، GB; Ramser, JH مشکل دیسپاچینگ کامیون. مدیریت علمی ۱۹۵۹ ، ۶ ، ۸۰-۹۱٫ [ Google Scholar ] [ CrossRef ]
التابیب، AM; محسن، ع.م. Ghalab, A. یک الگوریتم هیبریدی کرم شب تاب بهبود یافته برای مشکل مسیریابی وسیله نقلیه با ظرفیت. Appl. محاسبات نرم. ۲۰۱۹ ، ۸۴ ، ۱۰۵۷۲۸٫ [ Google Scholar ] [ CrossRef ]
جندرو، م. لاپورت، جی. پوتوین، جی.-ای. فراابتکاری برای VRP دارای ظرفیت. در مسئله مسیریابی خودرو ؛ SIAM: Philadelphia, PA, USA, 2002; صص ۱۲۹-۱۵۴٫ [ Google Scholar ]
لاپورت، جی. Semet، F. اکتشافی کلاسیک برای VRP دارای ظرفیت. در مسئله مسیریابی خودرو ؛ SIAM: Philadelphia, PA, USA, 2002; صص ۱۰۹-۱۲۸٫ [ Google Scholar ]
شیائو، ی. ژائو، کیو. کاکو، آی. Xu, Y. توسعه یک مدل بهینه‌سازی مصرف سوخت برای مشکل مسیریابی خودروی ظرفیت‌دار. محاسبه کنید. اپراتور Res. ۲۰۱۲ ، ۳۹ ، ۱۴۱۹-۱۴۳۱٫ [ Google Scholar ] [ CrossRef ]
هو، SC; Haugland, D. یک جستجوی اکتشافی تابو برای مشکل مسیریابی وسیله نقلیه با پنجره های زمانی و تحویل تقسیم شده. محاسبه کنید. اپراتور Res. ۲۰۰۴ ، ۳۱ ، ۱۹۴۷-۱۹۶۴٫ [ Google Scholar ] [ CrossRef ]
Karaoglan، AD; آتالای، من. Kucukkoc، I. مشکلات مسیریابی وسیله نقلیه محدود شده از راه دور: مطالعه موردی با استفاده از الگوریتم کلونی زنبور عسل مصنوعی. در مدلسازی ریاضی و بهینه سازی مسائل مهندسی ; Springer: Cham، سوئیس، ۲۰۲۰؛ صص ۱۵۷-۱۷۳٫ [ Google Scholar ]
ناگاراجان، وی. Ravi, R. الگوریتم های تقریب برای مسایل مسیریابی خودرو با محدودیت فاصله. Networks ۲۰۱۲ ، ۵۹ ، ۲۰۹-۲۱۴٫ [ Google Scholar ] [ CrossRef ]
عفیفی، س. دانگ، دی.-سی. Moukrim، A. الگوریتم بازپخت شبیه سازی شده برای مسئله مسیریابی وسیله نقلیه با پنجره های زمانی و محدودیت های همگام سازی. در مجموعه مقالات کنفرانس بین المللی یادگیری و بهینه سازی هوشمند، کاتانیا، ایتالیا، ۷-۱۱ ژانویه ۲۰۱۳٫ صص ۲۵۹-۲۶۵٫ [ Google Scholar ]
توث، پی. ویگو، دی. مسئله مسیریابی خودرو: انجمن ریاضیات صنعتی و کاربردی. سیام مونوگر. گسسته. ریاضی. Appl. ۲۰۰۱ . [ Google Scholar ] [ CrossRef ]
موسولینو، جی. ریندون، سی. Vitetta، A. جابجایی مسافران و بار با وسایل نقلیه الکتریکی: روشی برای برنامه ریزی حمل و نقل سبز و خدمات لجستیکی در نزدیکی مناطق بندری. ترانسپ Res. Procedia ۲۰۱۹ ، ۳۷ ، ۳۹۳-۴۰۰٫ [ Google Scholar ] [ CrossRef ]
موسولینو، جی. ریندون، سی. Vitetta، A. یک چارچوب مدل سازی برای شبیه سازی مسیرها و مسیرهای انتخاب وسایل نقلیه باری در مناطق حومه شهری. در مجموعه مقالات هفتمین کنفرانس بین المللی ۲۰۲۱ در مورد مدل ها و فناوری ها برای سیستم های حمل و نقل هوشمند (MT-ITS)، هراکلیون، یونان، ۱۶-۱۷ ژوئن ۲۰۲۱؛ صص ۱-۶٫ [ Google Scholar ]
لین، جی. ژو، دبلیو. Wolfson، O. مشکل مسیریابی وسایل نقلیه الکتریکی. ترانسپ Res. Procedia ۲۰۱۶ ، ۱۲ ، ۵۰۸-۵۲۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
موسولینو، جی. پولمنی، ع. Vitetta، A. مسیریابی وسیله نقلیه باری با زمان سفر پیوند قابل اعتماد: روشی مبتنی بر نمودار اساسی شبکه. ترانسپ Lett. ۲۰۱۸ ، ۱۰ ، ۱۵۹-۱۷۱٫ [ Google Scholar ] [ CrossRef ]
پولمنی، ع. Vitetta، A. مسیریابی خودرو در مناطق شهری: یک رویکرد بهینه با کالیبراسیون تابع هزینه. ترانسپ B Transp. دین ۲۰۱۴ ، ۲ ، ۱-۱۹٫ [ Google Scholar ] [ CrossRef ]
میرجلیلی، س. الگوریتم های تکاملی و شبکه های عصبی. در مطالعات هوش محاسباتی ; Springer: برلین، آلمان، ۲۰۱۹؛ جلد ۷۸۰٫ [ Google Scholar ]
وانگ، اس.-سی. الگوریتم ژنتیک. در محاسبات بین رشته ای در برنامه نویسی جاوا ; Springer: برلین، آلمان، ۲۰۰۳; صص ۱۰۱-۱۱۶٫ [ Google Scholar ]
جئون، جی. لیپ، منابع انسانی؛ Shim, JY یک مشکل مسیریابی وسیله نقلیه که با استفاده از یک الگوریتم ژنتیک ترکیبی حل شده است. محاسبه کنید. مهندس ۲۰۰۷ ، ۵۳ ، ۶۸۰-۶۹۲٫ [ Google Scholar ] [ CrossRef ]
برگر، جی. Barkaoui، M. یک الگوریتم ژنتیک ترکیبی برای مسئله مسیریابی وسیله نقلیه با ظرفیت. در مجموعه مقالات کنفرانس محاسبات ژنتیکی و تکاملی، شیکاگو، IL، ایالات متحده آمریکا، ۱۲-۱۶ ژوئیه ۲۰۰۳٫ صص ۶۴۶-۶۵۶٫ [ Google Scholar ]
ژو، دبلیو. آهنگ، تی. او، اف. لیو، ایکس. مسئله مسیریابی وسیله نقلیه چند هدفه با تعادل مسیر بر اساس الگوریتم ژنتیک. گسسته. دین نات. Soc. ۲۰۱۳ ، ۲۰۱۳ ، ۳۲۵۶۸۶٫ [ Google Scholar ] [ CrossRef ]
لو، ی. یین، ی. Lawphongpanich، S. برنامه ریزی استقرار گشت خدمات آزادراه برای مدیریت حادثه و کاهش ازدحام. ترانسپ Res. قسمت C Emerg. تکنولوژی ۲۰۱۱ ، ۱۹ ، ۲۸۳-۲۹۵٫ [ Google Scholar ] [ CrossRef ]
متیو، الگوریتم ژنتیک تلویزیون. گزارش ؛ ارسال شده در IIT Bombay؛ IIT Bombay: Powai، هند، ۲۰۱۲٫ [ Google Scholar ]
دب، ک. پراتاپ، ا. آگاروال، اس. میاریوان، تی. الگوریتم ژنتیک چندهدفه سریع و نخبه: NSGA-II. IEEE Trans. تکامل. محاسبه کنید. ۲۰۰۲ ، ۶ ، ۱۸۲-۱۹۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
موراتا، تی. Ishibuchi، H. MOGA: الگوریتم های ژنتیک چند هدفه. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد محاسبات تکاملی، پرت، استرالیا، ۲۹ نوامبر تا ۱ دسامبر ۱۹۹۵٫ ص ۲۸۹-۲۹۴٫ [ Google Scholar ]

شکل ۱٫ نمودار جریان الگوریتم ژنتیک بهبود یافته.

شکل ۲٫ شبکه راه برای منطقه مورد مطالعه.

شکل ۳٫ نمودار چکیده شبکه راه.

شکل ۴٫ مسیر اولیه قبل از بهینه سازی در سناریوی واقعی.

شکل ۵٫ مسیر نهایی پس از بهینه سازی در سناریوی واقعی.

ونوس نصیرفام

15 ژانویه 2023

مقالات