آیا Medoid برای میانگین مسیرهای GPS مناسب است؟

میانگین مسیرهای GPS در کاربردهایی مانند خوشه بندی و استخراج خودکار بخش های جاده مورد نیاز است. محاسبه میانگین برای مسیرها و سایر داده‌های سری زمانی غیرممکن است و نشان داده شده است که یک مسئله NP-hard است. بنابراین medoid به طور گسترده ای به عنوان یک جایگزین عملی و به دلیل تحمل نویز (فرض) بهتر مورد استفاده قرار گرفته است. در این مقاله، ما سودمندی مدوید را برای حل مسئله میانگین‌گیری با ده معیار مختلف مسیر-شباهت/-فاصله مطالعه می‌کنیم. نتایج ما نشان می‌دهد که دقت مدوید عمدتاً به حجم نمونه بستگی دارد. در مقایسه با سایر روش‌های میانگین‌گیری، عملکرد بدتر می‌شود، به‌ویژه زمانی که تنها نمونه‌های کمی وجود داشته باشد که باید مدوید از بین آنها انتخاب شود. ضعف دیگر این است که medoid ویژگی هایی مانند فراوانی نمونه نمونه انتخابی خودسرانه را به ارث می برد. انتخاب تابع فاصله مسیر کمتر قابل توجه است. برای کاربردهای عملی، روش‌های میانگین‌گیری دیگر به جز medoid جایگزین بهتری برای دقت بالاتر به نظر می‌رسد.

کلید واژه ها:

مدوید ; مسیرهای GPS ; میانگین گیری بخش ; توالی میانگین گیری ; HC-SIM ; موارد پرت

چکیده گرافیکی

۱٫ مقدمه

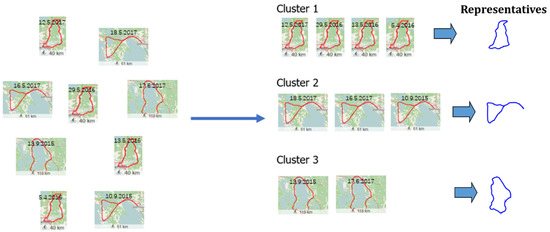
میانگین سیگنال‌های سری زمانی یک مشکل باز است که راه‌حل‌هایی برای آن در بسیاری از کاربردهای عملی مانند خوشه‌بندی مسیر [ ۱ ، ۲ ] و استخراج بخش‌های جاده از ضبط‌های سیستم موقعیت‌یابی جهانی (GPS) مورد نیاز است [ ۳ ، ۴ ، ۵ ]. شکل ۱ و شکل ۲ را ببینید . میانگین را می توان به عنوان نقطه ای در فضای داده تعریف کرد که فاصله مجذور از همه نقاط داده را به حداقل می رساند. با این حال، یافتن میانگین بهینه برای دنباله ها زمان بر است زیرا تعداد نمایی از نامزدها برای میانگین وجود دارد. نشان داده شده است که این یک مشکل محاسباتی (NP-hard) در مورد فضای DTW [6 ]، که برای حل بهینه نیاز به زمان نمایی دارد.

توالی‌های GPS با سری‌های زمانی متفاوت هستند زیرا تراز نقطه‌ای در فضای جغرافیایی ۲ بعدی (طول جغرافیایی، طول جغرافیایی) به جای فضای زمانی ۱ بعدی انجام می‌شود. مکان‌های مکانی نقاط از داده‌ها تشکیل می‌دهند و مهرهای زمانی آن‌ها در اینجا حذف می‌شوند. اگر شامل شود، مشکل تبدیل به میانگین توالی ها در فضای ۳ بعدی می شود. مسیرهای GPS همچنین می توانند به دلیل خطاهای GPS بسیار پر سر و صدا باشند [ ۷ ]. بنابراین، دو چالش اصلی مسئله میانگین گیری این است که (۱) نقاط منفرد با هم تراز نیستند، و (۲) تعداد نقاط می تواند به طور قابل توجهی بین دنباله های مختلف متفاوت باشد. حتی نسخه ۱ بعدی ساده شده با سیگنال با طول ثابت یک مشکل محاسباتی دشوار و NP-hard است.

Medoid یک جایگزین عملی برای میانگین گیری است. به طور گسترده در بسیاری از کاربردها در داده کاوی فضایی، دسته بندی متن، مسیریابی وسایل نقلیه و خوشه بندی استفاده شده است . به عنوان جسمی در مجموعه تعریف می شود که میانگین فاصله آن تا تمام اشیاء خوشه حداقل است [ ۱۲ ]. مفهومی شبیه به معنی استبا این تفاوت که میانگین می تواند هر نقطه ای از فضای داده باشد در حالی که medoid محدود شده است تا یکی از اشیاء در مجموعه باشد. Medoid زمانی استفاده می شود که میانگین را نمی توان به راحتی تعریف کرد، یا زمانی که میانگین گیری ساده می تواند ترکیبات مصنوعی ایجاد کند که در زندگی واقعی ظاهر نمی شوند. Medoid در مقایسه با میانگین دو مزیت اصلی دارد. اول، فقط k کاندید برای انتخاب وجود دارد که آن را از نظر محاسباتی قابل حل می کند. ثانیاً، انتظار می‌رود که در داده‌ها کمتر مورد تعصب قرار گیرد.

در خوشه بندی، medoid برای جایگزینی الگوریتم k-means شناخته شده [ ۱۳ ، ۱۴ ] با نوع قوی تر آن به نام k-medoids [ ۱۵ ] استفاده شده است، با این فرض که در برابر نویز قوی تر است. مشابه k-means، ابتدا نمایندگان خوشه ها را به صورت تصادفی انتخاب می کند. دوم، نزدیکترین نمایندگان جستجو می شوند و هر نقطه به خوشه ای با نزدیکترین نماینده تقسیم می شود. سپس مجموعه جدیدی از نمایندگان به عنوان مدوید برای هر خوشه محاسبه می شود. این فرآیند به طور مشابه در k-means تکرار می شود.

K-means خود فقط یک تنظیم کننده دقیق محلی است و اگر تعداد خوشه ها زیاد باشد عملکرد ضعیفی دارد. استفاده از روش اولیه سازی هوشمندانه یا راه اندازی مجدد الگوریتم چندین بار می تواند نتیجه را بهبود بخشد، اما تنها در صورتی که خوشه ها به طور کامل از هم جدا نشده باشند [ ۱۶ ]. این را می توان با یک بسته بندی ساده در اطراف k-means، به نام مبادله تصادفی [ ۱۷ ]، که مرکزها را به روش آزمون و خطا تعویض می کند، اما هر زمان که داده ها دارای خوشه هستند، مکان درست مرکز را پیدا کند [ ۱۸ ] قابل غلبه بر می باشد. گسترش مشابهی به k-medoid نیز با روشی به نام پارتیشن بندی در اطراف medoid (PAM) اعمال شده است [ ۱۵ ].

نتیجه جالب دیگری در [ ۱۹ ] هنگام مقایسه عملکرد k-means و مبادله تصادفی با داده های پر سر و صدا یافت شد. مبادله تصادفی به طور قابل توجهی با داده های تمیز بهتر کار می کند، اما زمانی که میزان نویز افزایش می یابد، برتری مبادله تصادفی حذف می شود و هر دو الگوریتم به همان اندازه ضعیف عمل می کنند. در واقع، k-means از نویز سود می برد، زیرا همپوشانی بیشتری بین خوشه ها ایجاد می کند، که به k-means کمک می کند تا مرکزها را بین خوشه ها حرکت دهد [ ۲۰ ]. این یافته‌ها نشان می‌دهند که استحکام نویز هر روشی کاملاً بدیهی است و تأثیر آن می‌تواند چیزی غیر از آن چیزی باشد که از عقل سلیم انتظار می‌رود.

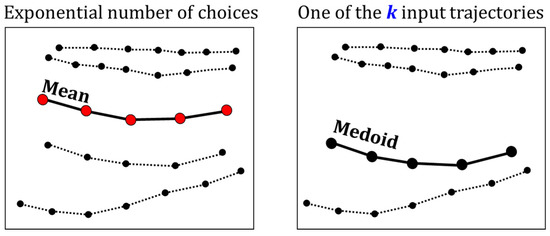
تفاوت بین میانگین و medoid در شکل ۳ نشان داده شده استبا مجموعه ای از چهار مسیر. Medoid یکی از مسیرهای ورودی است که می تواند کاربرد آن را در مجموعه های کوچک محدود کند. در این مورد، مکان بهینه میانگین جایی در میان است، اما هیچ مسیر نامزد مناسبی برای انتخاب وجود ندارد. medoid فقط بهترین در بین گزینه های موجود است. انتظار می رود که Medoid به خوبی کار کند اگر مسیرهای کافی در مجموعه برای انتخاب وجود داشته باشد. Medoid مشکلات دیگری نیز دارد. از آنجایی که یک نمونه از مجموعه ورودی است، تمام خصوصیات نمونه انتخابی (هم خوب و هم بد) را خواهد داشت. فاصله تا مسیرهای دیگر را به حداقل می رساند، اما سایر خصوصیات مانند فرکانس نمونه، طول یا شکل مسیرها را میانگین نمی کند. اینها ممکن است عملکرد آن را در عمل بدتر کنند.

علیرغم مزایای بالقوه مدوید، نتایج عملی در [ ۷] کاملاً دلسرد کننده بودند. همه اکتشافی‌های میانگین‌گیری مطالعه‌شده بدون توجه به تابع فاصله، به طور قابل‌توجهی بهتر از medoid عمل کردند. با این حال، medoid صرفاً به عنوان یک روش مرجع مورد استفاده قرار گرفت و واقعاً به طور جدی مورد توجه قرار نگرفت، در حالی که تمام اکتشافات ارسالی به دقت برای چالش میانگین‌گیری بخش تنظیم شده بودند. بنابراین این یک سوال باز است که آیا medoid واقعاً بسیار ضعیف است یا اینکه آیا می‌توان آن را برای عملکرد بهتر با استفاده از همان ترفندهای پیش پردازش و حذف موارد بیرونی که در روش‌های دیگر استفاده می‌شد تنظیم کرد. برای یافتن پاسخ به این سؤالات، ما یک مطالعه سیستماتیک در مورد سودمندی medoid برای مشکل میانگین‌گیری انجام دادیم. هدف ما پاسخ به سوالات زیر بود:

دقت مدوید چقدر است؟
چه زمانی کار می کند و چه زمانی نه؟
آیا در مورد داده های نویزدار بهتر از تکنیک های میانگین گیری موجود کار می کند؟
کدام تابع شباهت بهتر عمل می کند و انتخاب چقدر اهمیت دارد؟

بقیه مقاله به شرح زیر سازماندهی شده است. مشکل در بخش ۲ تعریف شده است و چندین گزینه را توضیح می دهد. Medoid در بخش ۳ تعریف شده است و بررسی مختصری در مورد آثار موجود با استفاده از medoid ارائه شده است. مجموعه داده ها و ابزارهای مورد استفاده برای آزمایش ها در بخش ۴ توضیح داده شده است. سپس نتایج اصلی در بخش ۵ گزارش شده و سپس تجزیه و تحلیل دقیق تر در بخش ۶ ارائه می شود . نتیجه گیری در بخش ۷ .

۲٫ میانگین گیری بخش

کار میانگین‌گیری به ظاهر ساده است، زیرا محاسبه میانگین اعداد بی‌اهمیت است، و تعمیم آن از اسکالر به بردار در تحلیل داده‌های چند متغیره آسان است. با این حال، میانگین سری های زمانی به طور قابل توجهی چالش برانگیزتر است، زیرا نقاط نمونه لزوماً همسو نیستند. حل مسئله میانگین‌گیری با استفاده از میانگین امکان‌پذیر است، که به عنوان هر دنباله ممکن در فضای داده تعریف می‌شود که مجموع فاصله‌های مجذور تمام توالی‌های ورودی را به حداقل می‌رساند [ ۷ ]:

(۱)

در اینجا X = { x _۱ , x _۲ , …, x _k } مجموعه ورودی نمونه و C میانگین آنهاست که به آن مرکز نیز می گویند . با این حال، فضای جستجو بسیار زیاد است و جستجوی جامع از طریق شمارش امکان پذیر نیست. برخی از نویسندگان مشکل را چنان چالش برانگیز می دانند که فکر می کنند بدیهی نیست که میانگین وجود داشته باشد [ ۶ ، ۲۱ ]. با این حال، قضیه کاهش آنها نشان داد که میانگین برای مجموعه ای از فضاهای تابش زمانی پویا (DTW) وجود دارد [ ۶ ]] و اکتشافی های موجود، بنابراین، توجیه نظری دارند. یک الگوریتم زمان نمایی برای حل دقیق میانگین DTW اخیراً در [ ۲۲ ] پیشنهاد شده است. مسیرهای GPS از چند جهت با سری های زمانی متفاوت است. ابتدا، هم ترازی سری های زمانی در حوزه زمانی انجام می شود، در حالی که نقاط GPS باید در فضای جغرافیایی تراز شوند. دوم، داده‌های GPS می‌توانند بسیار پر سر و صدا باشند، به این معنی که حتی ممکن است میانگین بهترین راه‌حل برای مشکل میانگین‌گیری نباشد.

۲٫۱٫ اکتشافی برای یافتن میانگین بخش

به دلیل دشواری یافتن میانگین بهینه، چندین اکتشافی سریعتر اما کمتر از بهینه توسعه یافته است. در [ ۱۳ ]، بخش های متوسط (به نام خط مرکزی ) برای خوشه بندی k-means مسیرهای GPS برای شناسایی خطوط جاده استفاده شد. روش میانگین گیری در مقاله تعریف نشده بود، اما بعداً در [ ۲۳ ] به عنوان رگرسیون خطی تکه ای توصیف شد . نقاط به عنوان یک مجموعه نامرتب در نظر گرفته می شوند و چند جمله ای های تکه تکه با شرایط پیوستگی در نقاط گره تناسب دارند [ ۲۴ ]. نقطه ضعف روش رگرسیون این است که ترتیب امتیازات از بین می رود و می تواند حل مشکل را حتی سخت تر کند.

روش میانگین‌بخشی بخش CellNet [ ۲۵ ] کوتاه‌ترین مسیر را به‌عنوان راه‌حل اولیه [ ۲۶ ] انتخاب می‌کند که به‌طور مکرر توسط الگوریتم عمده‌سازی-به حداقل رساندن [ ۱ ] بهبود می‌یابد. نمودار جعبه مسیر یک رویکرد تکراری مشابه است، که مسیرها را با خوشه‌بندی به بخش‌های فرعی تقسیم می‌کند و سپس، در هر مرحله، میانگین‌گیری تکه‌ای از بخش‌های فرعی را انجام می‌دهد [ ۲۷ ]. میانگین‌گیری الاستیک زمانی هسته‌ای (iTEKA) الگوریتم تکراری دیگری برای مسئله میانگین‌گیری است [ ۲۸ ]]. تمام مسیرهای هم ترازی ممکن را در نظر می گیرد و یک اصل هم ترازی رو به جلو و عقب را به طور مشترک ادغام می کند. چندین الگوریتم معقول در ادبیات وجود دارد، اگرچه بسیاری از آنها از پیچیدگی زمانی درجه دوم رنج می برند و اجرای آنها می تواند نسبتاً پیچیده باشد.

این مشکل در چالش اخیر میانگین‌گیری بخش ( http://cs.uef.fi/sipu/segments/ ، در ۲۴ نوامبر ۲۰۲۱ مشاهده شد) که در آن چندین روش اکتشافی ارائه و با یکدیگر مقایسه شدند، پرداخته شد. یک خط پایه جدید نیز با ترکیب بهترین اجزای روش ها از رقابت ساخته شد، همانطور که در شکل ۴ خلاصه شده است. اولین گام این است که مسیرها را دوباره مرتب کنید تا آنها را نسبت به ترتیب سفر تغییر ندهند. در مرحله دوم برای کاهش اثر مسیرهای پر سر و صدا، حذف بیرونی اعمال می شود. این مراحل مشکل را به یک مسئله میانگین‌گیری توالی استاندارد و الگوریتم عمده‌سازی-به حداقل رساندن کاهش می‌دهند [ ۱] سپس اعمال می شود. آخرین مرحله (اختیاری) صرفاً ساده کردن نمایش نهایی توسط الگوریتم چند ضلعی داگلاس-پوکر [ ۲۹ ] است.

۲٫۲٫ مدوید

میانه اغلب به جای متوسط استفاده می شود زیرا حساسیت کمتری به نویز دارد. در مورد مقادیر اسکالر، میانه را می توان به راحتی با مرتب سازی n مقدار داده و سپس انتخاب مقدار میانی از لیست مرتب شده به دست آورد. با این حال، داده‌های چند متغیره فاقد نظم طبیعی هستند، که یافتن مقدار «وسط» را دشوار می‌کند. میانه فضایی [ ۳۰ ] میانه را برای هر مقدار اسکالر به طور جداگانه می سازد و نتیجه الحاق میانه های اسکالر مستقل است. با این حال، مسیرهای GPS می‌توانند طول‌های متغیری داشته باشند و نقاط منفرد را نمی‌توان به‌طور پیش پاافتاده برای مطابقت با نقاطی که میانه باید از آن‌ها محاسبه کرد، تراز کرد.

می توان میانه را به عنوان یک مسئله کمینه سازی نیز تعریف کرد به طوری که میانه نقطه ورودی است که حداقل فاصله متوسط را با سایر نقاط مجموعه دارد. تعمیم این به داده های چند متغیره به عنوان medoid شناخته می شود . به عنوان یک شی داده ورودی تعریف می شود که فاصله کلی آن با سایر مشاهدات حداقل است. مزیت اصلی آن این است که مشکل سپس مشکل جستجوی خطی را کاهش می دهد: شی ورودی را پیدا کنید که این هدف کمینه سازی را برآورده می کند. به طور رسمی، ما medoid را به عنوان [ ۷ ] تعریف می کنیم:

(۲)

که در آن D یک تابع فاصله یا شباهت بین دو مسیر GPS x _i و x _j است. به عبارت دیگر، medoid به عنوان یک مسئله بهینه سازی تعریف می شود، مشابه آنچه که ما میانگین را در معادله (۱) تعریف کردیم. تفاوت این است که، به جای اجازه دادن به هر مسیر احتمالی در فضا، مدوید محدود می شود تا یکی از مسیرهای ورودی باشد. این امر فضای جستجو را به میزان قابل توجهی کاهش می‌دهد و پیچیدگی زمانی نظری یافتن مدوید می‌تواند به اندازه O( nk ^۲ ) باشد که k تعداد مسیرها و n تعداد نقاط در طولانی‌ترین مسیر است.

این تعریف همچنین مستلزم آن است که ما یک تابع فاصله معنادار بین اشیاء داده داشته باشیم. این پیچیدگی زمانی را افزایش می دهد زیرا محاسبه فاصله بین مسیرها بی اهمیت نیست. ^با توجه به k مسیرهای هر کدام از n نقطه، اکثر توابع فاصله O( ⁿ²) زمان می برند، که باعث پیچیدگی زمانی مدوید O(k2n2 ⁾می شود . با این حال، برخی از معیارها دارای انواع سریع‌تر مانند Fast-DTW [ ۳۱ ] هستند که می‌تواند این را به O( ^k2n) کاهش دهد .

۲٫۳٫ ترکیبی از اکتشافی و Medoid

در [ ۳۲ ]، یک روش ترکیبی با ترکیب یک میانگین اکتشافی ساده برای بخش های خطی و روش دیگری برای منحنی های پیچیده تر پیشنهاد شد. مدل خطی از سه توصیفگر استفاده می کند: منبع (S)، میانه (M) و مقصد (D). این روش ابتدا پیچیدگی بخش را بر اساس سه توصیف کننده تحلیل می کند تا تخمین بزند که آیا می توان از مدل خطی ساده استفاده کرد یا باید از جایگزین پیچیده تر استفاده کرد. Medoid به عنوان روش جایگزین در گونه ای به نام RapSeg-B استفاده شد. شکل ۵ (سمت چپ) ساختار کلی روش ترکیبی را نشان می دهد.

این روش سه مجموعه مجزا ایجاد می کند. نقاط پایانی هر مسیر ابتدا با k-means جمع آوری و خوشه بندی می شوند تا دو مجموعه تشکیل شود: مجموعه مبدا و مجموعه مقصد . جهت سفر نادیده گرفته می شود، اما خود ایده تعمیم می یابد حتی اگر مسیرها حفظ شوند. مجموعه سوم به نام مجموعه میانی از نقاط میانی مسیرها ایجاد می شود. سپس مرکزها برای هر یک از سه مجموعه برای ایجاد سه توصیفگر (S، M، D) محاسبه می شوند، همانطور که در شکل ۵ وجود دارد.(درست). برای تصمیم گیری در مورد اینکه آیا می توان از مدل خطی استفاده کرد، یک SD خط مستقیم با SMD چند ضلعی سه نقطه ای مقایسه می شود که از طریق نقطه میانی M یک انحراف ایجاد می کند. مدل برای توصیف این بخش مناسب است. این با کسینوس زاویه ∠SDM و ∠DSM اندازه گیری می شود. اگر کوچکتر از یک آستانه باشد، از medoid استفاده می شود.

۳٫ اقدامات شباهت

Medoid به عنوان مسیری در مجموعه تعریف می شود که فاصله کل را به حداقل می رساند (یا شباهت کل را به حداکثر می رساند) با سایر مسیرهای مجموعه. برای این، ما باید یک اندازه گیری فاصله یا شباهت را انتخاب کنیم. تاب خوردگی زمانی دینامیک احتمالاً رایج ترین است، اما به نمونه برداری فرعی، نویز و جابجایی نقطه حساس است. با توجه به [ ۵ ]، همچنین با قضاوت انسان همبستگی خوبی ندارد. در ادامه به طور مختصر معیارها را شرح می‌دهیم و سپس با استفاده از تمام این معیارها، میانگین‌گیری بخش را به طور گسترده مقایسه می‌کنیم. اقدامات و خواص آنها در جدول ۱ خلاصه شده است.

۳٫۱٫ شباهت سلولی (C-SIM)

شباهت سلولی (C-SIM) از یک شبکه برای محاسبه شباهت استفاده می کند. ابتدا نمایش سلولی مسیرها را ایجاد می‌کند و سپس شمارش می‌کند که دو مسیر چند سلول مشترک را نسبت به تعداد کل سلول‌های منحصربه‌فردی که اشغال می‌کنند، می‌شمارد [ ۵ ]. مزیت این روش این است که بسیار کمتر تحت تأثیر تغییر در نرخ نمونه برداری، جابجایی نقطه و نویز قرار می گیرد. یک اشکال این است که روش ترتیب سفر را نادیده می گیرد، اما یک توسعه اخیر برای حساس کردن آن به جهت در [ ۴۱ ] پیشنهاد شده است.

۳٫۲٫ شباهت سلول سلسله مراتبی (HC-SIM)

شباهت سلسله مراتبی سلول (HC-SIM) C-SIM را به سطوح زوم چندگانه گسترش می دهد. ایده این است که اگر منحنی ها در سطوح بالاتر تطابق خوبی داشته باشند، می توان تفاوت های کوچک را تحمل کرد. شکل ۶ را ببینید . C-SIM از شبکه ای به ابعاد ۲۵×۲۵ متر استفاده می کند و تعداد سلول هایی را که بخش به اشتراک می گذارد نسبت به تعداد کل سلول هایی که اشغال می کند، شمارش می کند. HC-SIM از شش سطح بزرگ‌نمایی با اندازه‌های شبکه ۲۵×۲۵ متر، ۵۰×۵۰ متر، ۱۰۰×۱۰۰ متر، ۲۰۰×۲۰۰ متر، ۴۰۰×۴۰۰ متر و ۸۰۰×۸۰۰ متر استفاده می‌کند. در مورد داده های نرمال شده به مقیاس (۰،۱) از اندازه های زیر استفاده می شود: ۰٫۵٪، ۱٪، ۲٪، ۴٪، ۸٪، ۱۶٪. سپس شمارش های فردی خلاصه می شود. با توجه به دو مسیر A و B، شباهت سلولی سلسله مراتبی آنها (با سطوح زوم L ) به صورت زیر محاسبه می شود [ ۷ ]:

(۳)

۳٫۳٫ فاصله ی اقلیدسی

فاصله اقلیدسی [ ۳۹ ] یکی از ساده ترین روش های ممکن است. فاصله بین نقاط دارای شاخص یکسان را محاسبه می کند. مزایای اصلی آن سادگی و تغییر ناپذیری در سفارش سفر است. تنها چالش این است که نقاط GPS (طول و عرض جغرافیایی) ابتدا باید به مختصات دکارتی تبدیل شوند. زمانی که نرخ نمونه برداری از دو مسیر بسیار متفاوت است، یا زمانی که این دو مسیر مشابه هستند اما یکی از آنها بسیار طولانی تر است، این اندازه گیری احتمالاً شکست می خورد. مشکل عدم همسویی نقاط است که در تمام اقدامات دیگر به یک شکل به آن پرداخته شده است.

۳٫۴٫ طولانی ترین دنباله متداول (LCSS)

طولانی ترین زیر دنباله مشترک (LCSS) در ابتدا برای شباهت رشته طراحی شده بود. طولانی ترین دنباله متداول برای رشته های GET EG، GE G T G، GE GET GET است . مزیت اصلی فاصله LCSS بین دو مسیر این است که اجازه می‌دهد نقاط GPS دور (پر سر و صدا) را بدون همتای خود رها کنید، تنها با یک جریمه جزئی در امتیاز [ ۴۲ ]. چنین نقاط نویز می تواند تأثیر عمده ای بر اندازه گیری های فاصله ای داشته باشد که نیاز به تطبیق جفت هر نقطه دارد.

۳٫۵٫ ویرایش فاصله در دنباله واقعی (EDR)

فاصله ویرایش روی دنباله واقعی (EDR) [ ۳۵ ] از فاصله ویرایش لوونشتاین [ ۴۳ ] مشتق شده است. تعداد عملیات درج، حذف و جایگزینی مورد نیاز برای تبدیل یک رشته به رشته دیگر را محاسبه می کند. به عنوان مثال، هنگام تبدیل تلخی به نشسته ، ابتدا b را به s ( sitter ) و سپس e را با i ( sittir ) و r را با n ( sittin ) جایگزین می کنیم و در آخر درج می کنیم. g ” و در پایان ( نشسته). بنابراین فاصله لونشتاین ۴ است. EDR با اعلام دو نقطه یکسان در صورتی که در فاصله ε از یکدیگر باشند، فاصله ویرایش را برای مسیرها اعمال می کند. در این مقاله مقدار ε ۰٫۰۵ است. در مقایسه با فاصله اقلیدسی، اثر نویز را کاهش می دهد، اما هر دو LCSS و EDR به نمونه برداری فرعی بسیار حساس هستند.

۳٫۶٫ تاب خوردگی زمانی پویا (DTW)

تاب خوردگی زمانی پویا (DTW) [ ۴۴ ] مشابه فاصله ویرایش است اما به جای تطبیق دقیق، فاصله بین نقاط مطابق را محاسبه می کند. معمولاً برای محاسبه فاصله سری های زمانی با طول های مختلف استفاده می شود و به طور مستقیم در مسیرهای GPS نیز اعمال می شود. اشکال DTW این است که به نرخ نمونه برداری حساس است.

۳٫۷٫ ویرایش فاصله با جریمه واقعی (ERP)

ویرایش فاصله با مجازات واقعی [ ۳۷ ] یک نوع متریک از EDR است که شبیه DTW است. فاصله بین نقاط همسان را محاسبه می کند. با این حال، در مورد یک موقعیت غیر منطبق، به جای استفاده از مقدار باینری (۰/۱) به عنوان EDR یا محاسبه فاصله تا نقاط همسایه به عنوان DTW، از ثابت ۱ استفاده می کند. این اصلاح، اندازه گیری را متریک می کند و امکان استفاده از ویژگی نابرابری مثلثی در جستجوها و ایجاد ساختارهای نمایه سازی کارآمد مانند درختان B+ را فراهم می کند.

۳٫۸٫ فاصله های فرشه و هاسدورف

فاصله هاسدورف [ ۴۵ ] حداکثر فاصله تمام نزدیکترین نقاط در دو مسیر است. فقط به طولانی ترین فاصله اهمیت می دهد و بنابراین به نویز، تفاوت در سرعت نمونه برداری و جابجایی نقطه حساس است. یک نقطه نویز منفرد می تواند فاصله را بسیار بزرگ کند حتی اگر مسیرها در غیر این صورت کاملاً مطابقت داشته باشند. فاصله Fréchet [ ۴۰ ] مانند Hausdorff است اما امتیازها را نمی توان با امتیازات گذشته مطابقت داد. بنابراین Fréchet ترتیب سفر را اجرا می کند در حالی که Hausdorff نسبت به آن تغییر نمی کند.

۳٫۹٫ فاصله مسیر درونیابی (IRD)

فاصله مسیر درونیابی (IRD) [ ۳۳ ] مشابه DTW است، با دو تفاوت اصلی. ابتدا، هنگامی که مسیر دیگر نمونه های کمتری در بخشی از مسیر دارد ، نقاط دو مسیر A و B را با استفاده از درون یابی جفت می کند. این می تواند تخمین فاصله بسیار دقیق تری را زمانی که دو مسیر دارای نرخ نمونه برداری متفاوت هستند، ارائه دهد. دوم، اجرای زمان خطی دارد، که باعث می‌شود به طور قابل‌توجهی سریع‌تر از اجرای ساده DTW زمان درجه دوم باشد.

۴٫ راه اندازی آزمایشی

ما میانگین‌گیری را با medoid با استفاده از داده‌های موجود از رقابت میانگین‌گیری بخش آزمایش می‌کنیم [ ۷ ]. جدول ۲ را ببینید . داده ها شامل بخش های استخراج شده از چهار مجموعه داده مسیر است: Joensuu 2015 [ ۵ ]، شیکاگو [ ۳ ]، برلین و آتن [ ۴ ]]. Joensuu 2015 بیشتر شامل مسیرهای پیاده روی، دویدن و دوچرخه است که توسط کاربران Mopsi جمع آوری شده است. دارای فرکانس نقطه بالا، به طور متوسط ۳ ثانیه، و داده ها به دلیل حرکت آهسته و تلفن های هوشمند پایین رده ای که برای جمع آوری داده ها استفاده می شوند، نویز دارند. شیکاگو شامل بخش های طولانی تر و ساده تر است که توسط اتوبوس شاتل دانشگاه جمع آوری شده است. برخی از بخش‌ها به دلیل ساختمان‌های بلند در کنار مسیر پر سر و صدا هستند که باعث پرش سیگنال GPS می‌شوند. داده ها در مجموعه آتن و برلین با ماشین با فرکانس نقطه بسیار پایین تر، ۴۲ ثانیه (برلین) و ۶۱ ثانیه (آتن) جمع آوری شد. این بخش‌ها ساده‌تر هستند و فقط چند نقطه دارند.

همه آزمایش ها با استفاده از دستگاه Dell R920 با ۴ × E7-4860 (مجموع ۴۸ هسته)، ۱ ترابایت، ۴ ترابایت SAS HD اجرا شد. زمان پردازش medoid با تمام اقدامات مشابه در همه موارد بیش از یک ساعت (> 1 ساعت) طول کشید، در حالی که روش مقایسه (پایه) تنها چند ثانیه طول کشید. به همین دلیل، ما زمان های دقیق را ثبت نکردیم، زیرا medoid به وضوح کندتر است.

ما عملکرد medoid را با یازده معیار تشابه به شرح زیر آزمایش می کنیم. ابتدا، میانگین های بخش را برای هر مجموعه با استفاده از medoid با اندازه گیری فاصله انتخاب شده تولید می کنیم. نتیجه با حقیقت زمینی با استفاده از HC-SIM مقایسه می‌شود، که به بهترین وجه با قضاوت انسان در [ ۷ ] مرتبط است. هر چه شباهت بیشتر باشد، نتیجه بهتر است. ما همچنین اثرات دو تکنیک پیش پردازش را آزمایش می کنیم: ترتیب مجدد نقاط و حذف نقاط پرت. انتظار می رود که سفارش مجدد اثر دستور سفر را از بین ببرد و اقدامات تحت تأثیر آن را بهبود بخشد. انتظار می‌رود که حذف قسمت‌های پرت در هنگام میانگین‌گیری مجموعه‌های پر سر و صدا کمک کند.

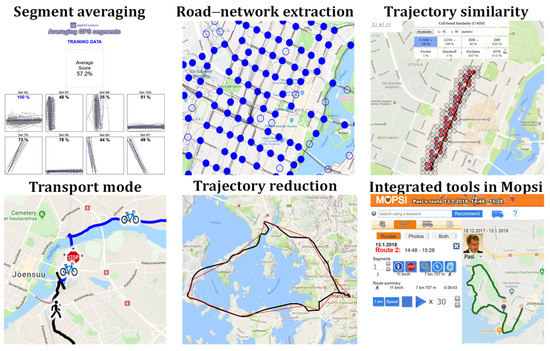
ما از ابزارهای وب Mopsi (نگاه کنید به شکل ۷ ) و API مربوطه در آزمایش استفاده می‌کنیم: http://cs.uef.fi/sipu/mopsi/ (در ۲۴ نوامبر ۲۰۲۱ قابل دسترسی است). اینها شامل صفحات وب مختلف برای نشان دادن عملکرد یک روش است. برخی اجازه آپلود داده‌های خود را می‌دهند و برخی دیگر APIهایی را ارائه می‌دهند که توسط افرادی که مهارت‌های برنامه‌نویسی کافی دارند استفاده شود. ابزارهای زیر حداقل در دسترس هستند:

میانگین گیری بخش [ ۷ ]

http://cs.uef.fi/sipu/segments/training.html (دسترسی در ۲۴ نوامبر ۲۰۲۱)
استخراج شبکه جاده ای [ ۲۵ ]

http://cs.uef.fi/mopsi/routes/network (دسترسی در ۲۴ نوامبر ۲۰۲۱)
شباهت مسیرها [ ۵ ]

http://cs.uef.fi/mopsi/routes/similarityApi/demo.php (دسترسی در ۲۴ نوامبر ۲۰۲۱)
تشخیص حالت حمل و نقل [ ۴۶ ]

http://cs.uef.fi/mopsi/routes/transportationModeApi (دسترسی در ۲۴ نوامبر ۲۰۲۱)
کاهش مسیر [ ۴۷ ]

http://cs.uef.fi/mopsi/routes/reductionApi (دسترسی در ۲۴ نوامبر ۲۰۲۱)
ابزارهای یکپارچه در Mopsi

http://cs.uef.fi/mopsi/ (دسترسی در ۲۴ نوامبر ۲۰۲۱)

صفحه وب با میانگین بخش مرتبط ترین است زیرا به کاربران اجازه می دهد الگوریتم خود را با داده های آموزشی با بارگذاری نتایج تقسیم بندی در قالب متن آزمایش کنند. این ابزار میانگین بخش های آپلود شده را تجسم می کند و امتیازات HC-SIM آنها را محاسبه می کند، اما فقط به ۱۰۰ داده آموزشی محدود می شود. داده های تست در دسترس هستند، اما نه از طریق این ابزار تعاملی. ابزار استخراج شبکه جاده، تقاطع ها و بخش های حاصل را در بین پنج الگوریتم نشان می دهد. این برنامه کاربردی را نشان می دهد که در آن میانگین گیری بخش مورد نیاز است. ابزار تشابه مسیر، عملکرد ۸ اندازه گیری فاصله (فقط تنها معیارهای اخیر، IRD و HC-SIM) را با هفت مجموعه داده از پیش انتخاب شده نشان می دهد. متأسفانه، در حال حاضر اجازه آزمایش با داده های خود کاربران را نمی دهد.

ابزار تشخیص حالت حمل و نقل به کاربران اجازه می دهد مسیرهای خود را آپلود کنند و بخش های شناسایی شده و نقاط توقف پیش بینی شده و انواع حرکت آنها (ماشین، دوچرخه، دویدن، پیاده روی) را خروجی می دهد. ابزار کاهش مسیر، تقریب چند ضلعی را برای مسیر ورودی کاربر با پنج سطح کیفی مختلف انجام می دهد. چندین ابزار دیگر به طور مستقیم در سیستم Mopsi بدون رابط های خاص یکپارچه شده اند، از جمله جستجوی شباهت مبتنی بر C-SIM [ ۵ ] و جستجوی مبتنی بر اشاره که در آن کاربر مسیر تقریبی را با ترسیم با دست آزاد وارد می کند [ ۴۸ ]]. به طور خلاصه، در حالی که اکثر نتایج در این مقاله توسط پیاده سازی های داخلی به دست آمده اند، API ها و ابزارهای وب مفیدی برای خواننده در دسترس هستند تا آزمایش های خود را مستقیماً مرتبط با پردازش مسیر GPS انجام دهند.

۵٫ نتایج

نتایج کلی داده های آموزشی و داده های آزمون بدون پیش پردازش در جدول ۳ خلاصه شده است که از بهترین به بدترین (داده های آموزشی) مرتب شده اند. نتایج حاصل از میانگین گیری بخش پایه نیز از [ ۷ ] گنجانده شده است. سه مشاهدات اصلی از نتایج عبارتند از:

HC-SIM بهترین عملکرد را با داده های آموزشی دارد.
انتخاب تابع فاصله فقط یک اثر جزئی دارد.
نتایج Medoid به طور قابل توجهی بدتر از میانگین پایه است [ ۷ ].

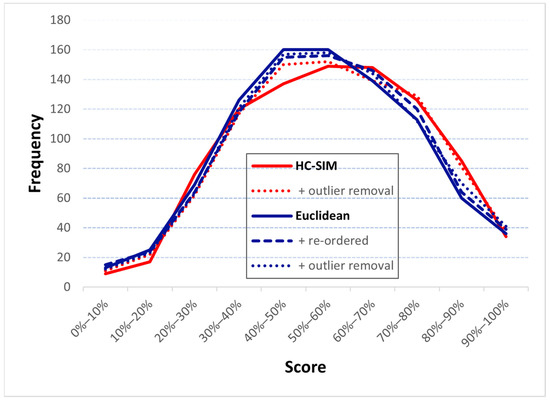
مشاهده اول تعجب آور نیست. انتظار می رود که بهینه سازی برای همان معیاری که در ارزیابی استفاده می شود بهترین عملکرد را داشته باشد و بنابراین منطقی است که از HC-SIM به عنوان معیار تشابه با medoid استفاده شود. اما مشاهده دوم مهمتر است. تفاوت بین بهترین (HC-SIM = 59.9٪) و بدترین (اقلیدسی = ۵۶٫۷٪) تنها ۳٫۲٪ واحد برای داده های آموزشی بدون پیش پردازش است. تفاوت (۵۵٫۷٪ در مقابل ۵۴٫۱٪) با داده های آزمون (۱٫۷٪) حتی کوچکتر می شود. توزیع امتیاز آنها نیز مشابه است. medoid با LCSS، DTW، EDR، C-SIM، و اقلیدسی دارای سگمنت‌های ضعیف‌تری است (<30٪) نسبت به HC-SIM، اما بیشتر سگمنت‌ها هنوز در بازه ۴۰-۷۰٪ هستند (از ۴۳۴ تا ۴۷۴ متغیر است). جدول ۴ و شکل ۸ را ببینید. مشاهده سوم مهم ترین است: همه این نتایج به طور قابل توجهی بدتر از میانگین میانگین پایه هستند که ۶۶٫۹٪ برای داده های آموزشی و ۶۲٫۱٪ برای داده های آزمایشی است [ ۷ ]. این نشان می‌دهد که علت اصلی عملکرد، خود مدوید است، نه معیار شباهت.

ما همچنین تأثیر ترتیب مجدد و حذف موارد پرت را تجزیه و تحلیل می کنیم. برای این موارد، از تکنیک‌های خط مبنا در [ ۷ ] استفاده می‌کنیم: k-means برای مرتب‌سازی مجدد، و معیار فاصله و طول برای حذف موارد پرت. توجه داشته باشید که اگر اندازه‌گیری فاصله نسبت به ترتیب سفر تغییر نمی‌کند، لزوماً نیازی به مرتب‌سازی مجدد ندارد. این مورد در مورد Hausdorff، C-SIM، و HC-SIM است. با این حال، سایر توابع فاصله به ترتیب نقطه حساس هستند: DTW، ERD، ERP، LCSS، Fréchet و Euclidean. در صورت استفاده از این موارد، ممکن است سفارش مجدد لازم باشد. با این حال، نتایج در جدول ۳نشان می دهد که در حالی که پیش پردازش نتایج را در بیشتر موارد بهبود می بخشد، اثر کلی متوسط باقی می ماند. مرتب‌سازی مجدد، Fréchet و Euclidean را اندکی بهبود می‌بخشد، به‌ویژه در مجموعه داده‌هایی که امتیاز میانگین بخش آن بین ۴۰% و ۹۰% کاهش می‌یابد ( جدول ۴ ). تشخیص های پرت نتایج EDR، DTW، FastDTW و LCSS را برای میانگین نمرات بین ۷۰ تا ۹۰ درصد بهبود می بخشد. به طور متوسط، میانگین عملکرد medoid از ۵۴٫۸٪ به ۵۴٫۹٪ بهبود می یابد، اما نتایج هنوز به طور قابل توجهی بدتر از روش میانگین بخش پایه در [ ۷ ] (۶۲٫۱٪) است، که نشان می دهد این دو تکنیک برای جبران کافی نیستند. برای نقاط ضعف مدوید

نتیجه IRD نشان می دهد که حذف پرت تأثیر قابل توجهی بر بسیاری از مجموعه داده های GPS ندارد. در موارد معدودی، حذف پرت اثرات مثبتی دارد، اما نه قابل توجه. میانگین نمرات مرتب شده مجدد برای C-SIM، HC-SIM و Hausdorff یکسان است.

۶٫ تجزیه و تحلیل دقیق

بعداً تأثیر پارامترهای مختلف مانند نویز و اندازه تنظیم، و تکنیک‌های پیش پردازش از جمله مرتب‌سازی مجدد، حذف موارد پرت و عادی‌سازی با نمونه‌گیری مجدد را تحلیل می‌کنیم.

۶٫۱٫ سر و صدا

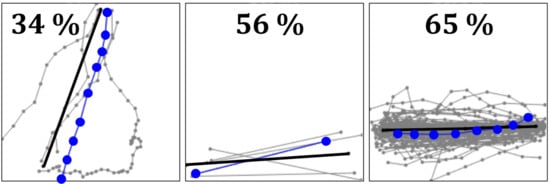
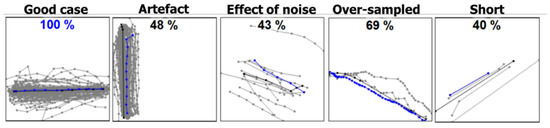
شکل ۹ چند نمونه را نشان می دهد که در آن مدوید انتخاب شده دارای ویژگی های غیرعادی است که داده ها را به خوبی توصیف نمی کند. به عنوان مرجع، اولین مثال (سمت چپ) موردی است که medoid بسیار خوب کار می کند. فاصله تا حقیقت زمین به ۱۰۰% می رسد و هیچ تفاوت قابل مشاهده ای بین آنها وجود ندارد. این مجموعه دارای نمونه های زیادی است و مدوید می تواند مسیری را انتخاب کند که از نظر بصری نیز دلپذیر است. موارد دیگر اما مشکلات متفاوتی را نشان می دهند.

مثال دوم (Artefact) در شکل ۹ممکن است انتخاب معقولی باشد، زیرا در وسط نمونه ها قرار دارد، حتی اگر کمی از حقیقت اصلی فاصله داشته باشد. با این حال، مسیر انتخاب شده دارای یک مصنوع ناخواسته در بالا با داشتن یک قله کوچک به سمت راست است. مثال سوم (Noise) اثر نویز را نشان می دهد. در حالی که انتظار می رود medoid در برابر نویز قوی تر از میانگین باشد، در عمل اینطور نیست. یک نمونه دور برای بیرون کشیدن مدوید از خط مرکزی کافی است و امتیاز را به ۴۳ درصد کاهش می دهد. مثال چهارم (Over-sampled) امتیاز نسبتاً خوبی دارد و از نظر بصری به واقعیت نزدیک است. مشکل این است که دارای تعداد قابل توجهی از نقاط نمونه است حتی اگر در غیر این صورت ممکن است ویژگی های میانگین گیری خوبی داشته باشد. مثال آخر (کوتاه) پدیده‌ای را نشان می‌دهد که در آن کوتاه‌ترین بخش به‌عنوان مدوید انتخاب می‌شود، علی‌رغم اینکه از بین همه گزینه‌ها بیرونی‌ترین بخش است.

۶٫۲٫ سفارش مجدد و حذف موارد پرت

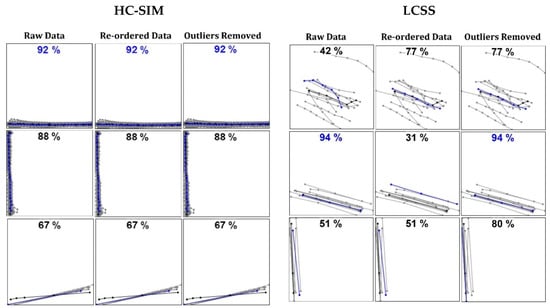
مجموعه های انتخاب شده در شکل ۱۰ نشان داده شده اند تا برخی از اثرات مرتب سازی مجدد و حذف موارد پرت را نشان دهند. مرتب کردن مجدد و حذف موارد پرت می تواند گهگاه کمک کند، به خصوص زمانی که از LCSS استفاده می شود، اما اثر با HC-SIM تقریباً تصادفی به نظر می رسد. حذف نقاط پرت نتوانست بسیاری از نقاط پرت را شناسایی کند. دلیل اصلی این است که فقط نقاط را تجزیه و تحلیل می کند، نه کل مسیرها. این یک پیشرفت بالقوه در آینده برای میانگین گیری بخش به طور کلی است، نه تنها با medoid.

۶٫۳٫ عادی سازی

ما بعداً تأثیر عادی‌سازی مسیرها را با نمونه‌برداری مجدد قبل از انتخاب medoid مطالعه می‌کنیم. شکل ۱۱ چهار مثال را نشان می دهد که داده های ورودی برای اولین بار پردازش می شوند به طوری که هر مسیر از همان تعداد نقطه تشکیل شده است (۱۰). می بینیم که در همه این موارد نتیجه هم از نظر بصری و هم با توجه به نمره عددی بهتر است. نتیجه هنوز هم مصنوعات مسیر انتخاب شده را کپی می کند، اما به دلیل پس پردازش، شدیدترین مصنوعات مانند نمونه برداری بیش از حد و اثر زیگ زاگ حذف شده اند.

۶٫۴٫ اندازه مجموعه ها

کمبود اصلی مدوید ناشی از کمبود داده برای انتخاب یک مدوید خوب است. HC-SIM، IRD و Hausdorff سه معیار شباهت هستند که با داده های آموزشی بهترین عملکرد را دارند، در حالی که HC-SIM، C-SIM و IRD بهترین عملکرد را با داده های آزمایشی دارند، از نظر نزدیک ترین به حقیقت زمین. با این حال، آنها همچنین دارای کمترین بخش با امتیاز کمتر از ۴۰٪ هستند. شکل ۱۲چند مورد را نشان می دهد که امتیاز زیر ۳۰٪ است. می بینیم که همه موارد فقط چند نمونه دارند. با این حال، مورد اول (مجموعه ۲۷) تنها سه نمونه مسیر دارد، که برای گرفتن بخش واقعی جاده (خط سیاه)، که از نمونه‌ها جدا شده است، بسیار کم هستند. مورد دوم (مجموعه ۸۷) دارای افست مشابه است، اما مثال سوم (مجموعه ۳۵) تمایل مدوید را به انتخاب کوتاه ترین بخش نشان می دهد، علیرغم این واقعیت که بخش طولانی تر در وسط معقول تر است. یک مشاهدات مهم این است که هر سه روش انتخاب های یکسانی دارند، بنابراین رفتار را می توان عمدتاً به خود مدوید نسبت داد، نه به انتخاب اندازه گیری فاصله.

۶٫۵٫ تعداد امتیاز

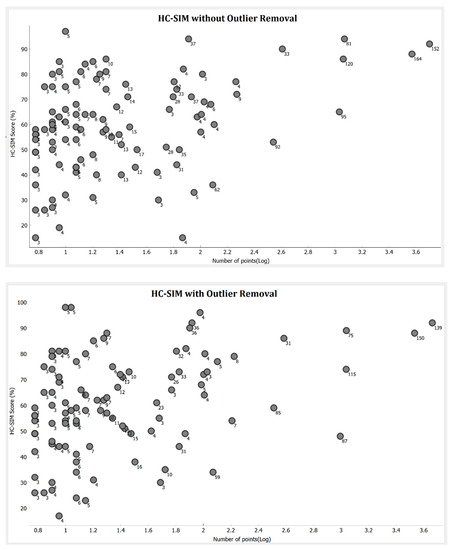
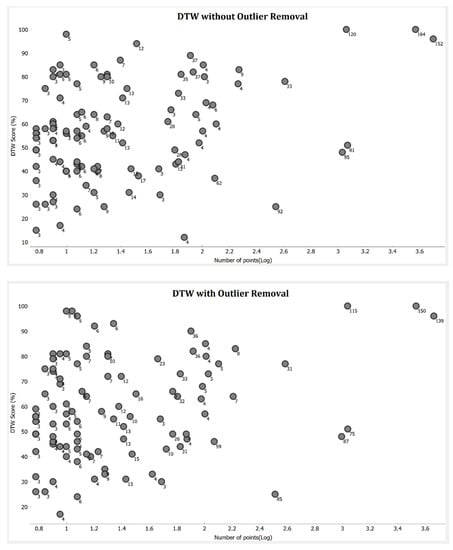
نتایج برای مجموعه های انتخاب شده با HC-SIM و DTW در شکل ۱۳ و شکل ۱۴ رسم شده است.برای نشان دادن تأثیر اندازه مجموعه و حذف موارد پرت. در اینجا عدد با دایره تعداد مسیرها را نشان می دهد و محور x مقدار لگاریتمی تعداد نقاط مجموعه است. نتایج نشان می دهد که عملکرد medoid با اندازه داده ها افزایش می یابد. ست هایی با تعداد امتیاز زیاد امتیازات به طور قابل توجهی بالاتری دارند و بیشتر ست های کم امتیاز ست هایی هستند که فقط مسیر و امتیاز کمی دارند. مشاهده می کنیم که تعداد مسیرها در مجموعه و تعداد نقاط در هر مسیر بر عملکرد مدوید تأثیر می گذارد. هر چه بیشتر = امتیاز و مسیر وجود داشته باشد، امتیاز بهتری کسب می کنید. حذف پرت باعث بهبود عملکرد برخی از مجموعه هایی می شود که مسیرها و نقاط کمی دارند.

۷٫ نتیجه گیری

استفاده از medoid برای میانگین‌گیری بخش‌های GPS به دلیل سادگی و مقاومت احتمالی آن برای نقاط پرت وسوسه‌انگیز است. با این حال، در واقعیت، از مشکلات متعددی رنج می برد که سودمندی آن را در عمل محدود می کند. ما در اینجا نقاط ضعف زیر را که در آزمایشات ما مشاهده شده است فهرست می کنیم:

دقت medoid به وضوح کمتر از بهترین میانگین اکتشافی (پایه) است.
برخلاف انتظارات، medoid در برابر نویز آسیب پذیر است.
Medoid تمایل دارد بخش های کوتاه را انتخاب کند.
Medoid ویژگی های (گاهی ناخواسته) مسیر اصلی را کپی می کند.
کند است (میانگین تمام ست ها بیش از ۱ ساعت طول می کشد).

Medoid در هنگام استفاده از معیار تشابه HC-SIM بدون پیش پردازش مجموعه داده، نمرات کیفیت ۵۹٫۹٪ (آموزش) و ۵۴٫۷٪ (آزمون) را ارائه می دهد. این بسیار کمتر از میانگین بخش پایه با ۶۶٫۹٪ (آموزش) و ۶۲٫۱٪ (آزمون) است. Medoid به خصوص زمانی که نمونه های کمی برای انتخاب وجود دارد، ضعیف عمل می کند. اگر اندازه مجموعه بزرگ باشد، شانس بیشتری برای یافتن نماینده دقیق تری وجود دارد. Medoid همچنین تمایل به انتخاب بخش های کوتاه دارد. فقط شکل کلی را به طور میانگین می گیرد اما سایر ویژگی ها مانند طول قطعه و تعداد نقاط نمونه را نادیده می گیرد. اینها به طور دلخواه از داده های اصلی انتخاب می شوند و بنابراین کیفیت medoid بستگی زیادی به کیفیت داده ها دارد.

به این دلایل، ما استفاده از medoid را توصیه نمی کنیم و میانگین اکتشافی موجود امیدوارکننده تر به نظر می رسد. از Medoid به خصوص زمانی که تعداد نمونه ها کم است باید اجتناب شود. برخی از نواقص آن را می توان با حذف نویز و عادی سازی مسیرهای ورودی با نمونه برداری مجدد برطرف کرد. این مراحل همچنین در سایر اکتشافی های میانگین گیری گنجانده شده است. سؤال اصلی دیگر طراحی، انتخاب بین میانگین‌گیری سریع توالی، مانند الگوریتم عمده‌سازی-به حداقل رساندن، یا الگوریتم زمان‌بر brute-force مورد نیاز medoid است. از نقطه نظر کارایی، دلیلی برای استفاده از medoid وجود ندارد. فقط زمانی که تعداد نمونه ها کم باشد سریع است، اما زمانی که کیفیت آن پایین است نیز چنین است.

اثر سنجش تشابه در درجه دوم اهمیت قرار داشت. HC-SIM بهترین عملکرد را داشت، اما با استفاده از تکنیک های پیش پردازش، نتایج بسیار به یکدیگر نزدیک شدند. میانگین نمرات پنج معیار با بهترین عملکرد (C-SIM، HC-SIM، IRD، EDR، LCSS) تنها در ۰٫۳٪ واحد از یکدیگر است (۵۶٫۰٪، ۵۵٫۹٪، ۵۵٫۹٪، ۵۵٫۷٪، ۵۵٫۷٪). ). به طور خلاصه، مشکل medoid انتخاب معیار تشابه نیست، بلکه محدودیت کلی خود medoid است، زیرا محدود به انتخاب یکی از مسیرهای ورودی به عنوان میانگین است. این محدودیت احتمالاً در سایر برنامه هایی که از medoid استفاده می شود ظاهر می شود.

منابع

هاوتاماکی، وی. نیکانن، پ. Fränti، P. خوشه بندی سری های زمانی توسط نمونه های اولیه تقریبی. در مجموعه مقالات کنفرانس بین المللی تشخیص الگو، تامپا، فلوریدا، ایالات متحده آمریکا، ۸-۱۱ دسامبر ۲۰۰۸٫ صص ۱-۴٫ [ Google Scholar ]
بوچین، ک. دریمل، ا. ون د لایل، ن. Nusser, A. Klcluster: Cluster-based Clustering of Trajectories. در مجموعه مقالات بیست و هفتمین کنفرانس بین المللی ACM SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی (SIGSPATIAL ’19)، شیکاگو، IL، ایالات متحده آمریکا، ۵ تا ۸ نوامبر ۲۰۱۹؛ صص ۴۹۶-۴۹۹٫ [ Google Scholar ]
بیاجیونی، جی. اریکسون، جی. استنتاج نقشه های راه از ردیابی سیستم موقعیت یابی جهانی: بررسی و ارزیابی مقایسه ای. ترانسپ Res. ضبط ۲۰۱۲ ، ۲۲۹۱ ، ۶۱-۷۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
احمد، م. کاراگیورگو، اس. Pfoser، D.; Wenk, C. مقایسه و ارزیابی الگوریتم‌های ساخت نقشه با استفاده از داده‌های ردیابی خودرو. GeoInformatica ۲۰۱۵ ، ۱۹ ، ۶۰۱-۶۳۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ماریسکو-ایستودور، آر. Fränti، P. روش مبتنی بر شبکه برای تجزیه و تحلیل مسیر GPS برای بازیابی. ACM Trans. تف کردن سیستم الگوریتم (TSAS) ۲۰۱۷ ، ۳ ، ۸٫ [ Google Scholar ] [ CrossRef ]
جین، بی جی; شولتز، دی. شرایط کافی برای وجود میانگین نمونه سری زمانی تحت تاب خوردگی زمانی پویا. ان ریاضی. آرتیف. هوشمند ۲۰۲۰ ، ۸۸ ، ۳۱۳-۳۴۶٫ [ Google Scholar ] [ CrossRef ]
فرانتی، پ. Mariescu-Istodor, R. میانگین رقابت بخش‌های GPS 2019. تشخیص الگو. ۲۰۲۱ , ۱۱۲ , ۱۰۷۷۳۰٫ [ Google Scholar ] [ CrossRef ]
استیویل-کاسترول، وی. موری، AT کشف ارتباط در داده‌های مکانی – یک رویکرد مبتنی بر مدوید کارآمد. در تحقیق و توسعه در کشف دانش و داده کاوی ; نکات سخنرانی در هوش مصنوعی; Springer: برلین/هایدلبرگ، آلمان، ۱۹۹۸; جلد ۱۳۹۴٫ [ Google Scholar ]
موکرجی، ا. باسو، تی. یک طرح وزن دهی مبتنی بر مدوید برای قاعده تصمیم گیری نزدیکترین همسایه به سمت طبقه بندی متن موثر. SN Appl. علمی ۲۰۲۰ ، ۲ ، ۱-۹٫ [ Google Scholar ] [ CrossRef ]
فرانتی، پ. Yang, J. Medoid-Shift برای حذف نویز برای بهبود خوشه بندی. در مجموعه مقالات کنفرانس بین المللی هوش مصنوعی و محاسبات نرم، زکوپان، لهستان، ۳ تا ۷ ژوئن ۲۰۱۸؛ Springer: Cham, Switzerland, 2018; صص ۶۰۴-۶۱۴٫ [ Google Scholar ]
پارک، اچ.-اس. جون، سی.-اچ. یک الگوریتم ساده و سریع برای خوشه بندی K-medoids. سیستم خبره Appl. ۲۰۱۹ ، ۳۶ ، ۳۳۳۶–۳۳۴۱٫ [ Google Scholar ] [ CrossRef ]
کافمن، ال. Rousseeuw, PJ یافتن گروه‌ها در داده‌ها: مقدمه‌ای بر تحلیل خوشه‌ای . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، ۲۰۰۹; جلد ۳۴۴٫ [ Google Scholar ]
واگستاف، ک. کاردی، سی. راجرز، اس. Schroedl, S. K-محدود به معنی خوشه بندی با دانش پس زمینه است. در مجموعه مقالات کنفرانس بین المللی یادگیری ماشین (ICML)، ویلیامزتاون، MA، ایالات متحده آمریکا، ۲۸ ژوئن تا ۱ ژوئیه ۲۰۰۱٫ جلد ۱، ص ۵۷۷–۵۸۴٫ [ Google Scholar ]
کریشنا، ک. الگوریتم مورتی، MN ژنتیک K-means. IEEE Trans. سیستم مرد سایبرن. قسمت B (سایبرن.) ۱۹۹۹ ، ۲۹ ، ۴۳۳-۴۳۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ون در لان، م. پولارد، ک. برایان، جی. الگوریتم پارتیشن بندی جدید پیرامون مدویدها. J. Stat. محاسبه کنید. شبیه سازی ۲۰۰۳ ، ۷۳ ، ۵۷۵-۵۸۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
فرانتی، پ. Sieranoja، S. چقدر می توان k-means را با استفاده از مقداردهی اولیه و تکرار بهتر بهبود بخشید؟ تشخیص الگو ۲۰۱۹ ، ۹۳ ، ۹۵-۱۱۲٫ [ Google Scholar ] [ CrossRef ]
Fränti، P. کارایی خوشه بندی مبادله تصادفی. J. Big Data ۲۰۱۸ , ۵ , ۱۳٫ [ Google Scholar ] [ CrossRef ]
رضایی، م. Fränti, P. آیا می توان تعداد خوشه ها را با شاخص های خارجی تعیین کرد؟ دسترسی IEEE ۲۰۲۰ ، ۸ ، ۸۹۲۳۹–۸۹۲۵۷٫ [ Google Scholar ] [ CrossRef ]
یانگ، جی. رهاردجا، س. Fränti، P. تشخیص و فیلتر کردن نقاط پرت میانگین تغییر. تشخیص الگو ۲۰۲۱ ، ۱۱۵ ، ۱۰۷۸۷۴٫ [ Google Scholar ] [ CrossRef ]
فرانتی، پ. Sieranoja، S. K-به معنی ویژگی‌ها در شش مجموعه داده معیار خوشه‌بندی است. Appl. هوشمند ۲۰۱۸ ، ۴۸ ، ۴۷۴۳-۴۷۵۹٫ [ Google Scholar ] [ CrossRef ]
شولتز، دی. جین، بی. تحلیل غیرهموار و روش‌های زیرگروهی برای میانگین‌گیری در فضاهای تاب‌دار زمانی پویا. تشخیص الگو ۲۰۱۸ ، ۷۴ ، ۳۴۰-۳۵۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بریل، ام. فلوشنیک، تی. فروس، وی. جین، بی. نیدرمایر، آر. شولتز، دی. محاسبه میانگین دقیق در فضاهای تاب دار زمان پویا. حداقل داده بدانید. کشف کنید. ۲۰۱۹ ، ۳۳ ، ۲۵۲-۲۹۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شرودل، اس. واگستاف، ک. راجرز، اس. لنگلی، پی. Wilson, C. استخراج ردیابی GPS برای اصلاح نقشه. حداقل داده بدانید. کشف کنید. ۲۰۰۴ ، ۹ ، ۵۹-۸۷٫ [ Google Scholar ] [ CrossRef ]
پیگل، ال. Tiller, W. The NURBS Book , ۲nd ed.; Springer: برلین/هایدلبرگ، آلمان، ۱۹۹۷٫ [ Google Scholar ]
ماریسکو-ایستودور، آر. Fränti، P. Cellnet: استنتاج شبکه های جاده از مسیرهای GPS. ACM Trans. تف کردن سیستم الگوریتم (TSAS) ۲۰۱۸ ، ۴ ، ۱-۲۲٫ [ Google Scholar ] [ CrossRef ]
فتحی، ع. Krumm, J. تشخیص تقاطع جاده ها از ردیابی GPS. در مجموعه مقالات کنفرانس بین المللی علم اطلاعات جغرافیایی، زوریخ، سوئیس، ۱۴-۱۷ سپتامبر ۲۰۱۰٫ Springer: برلین/هایدلبرگ، آلمان، ۲۰۱۰; صص ۵۶-۶۹٫ [ Google Scholar ]
اتین، ال. دووگل، تی. بوچین، م. مک آردل، جی. طرح جعبه مسیر: الگویی جدید برای خلاصه کردن حرکات. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۶ ، ۳۰ ، ۸۳۵-۸۵۳٫ [ Google Scholar ] [ CrossRef ]
Marteau، سری PF Times میانگین گیری و حذف نویز از دیدگاه احتمالی در هسته های الاستیک زمان. بین المللی J. Appl. ریاضی. محاسبه کنید. علمی ۲۰۱۹ ، ۲۹ ، ۳۷۵–۳۹۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
داگلاس، دی اچ. الگوریتم های Peucker، TK برای کاهش تعداد نقاط مورد نیاز برای نمایش یک خط دیجیتالی یا کاریکاتور آن. Cartographica ۱۹۷۳ , ۱۰ , ۱۱۲-۱۲۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
درزنر، ز. کلامروث، ک. شوبل، آ. Wesolowsky، GO مشکل وبر. در محل تاسیسات: کاربردها و تئوری ; Springer: Berlin/Heidelberg، آلمان، ۲۰۰۲٫ [ Google Scholar ]
سالوادور، اس. چان، پی. به سوی تاب برداشتن زمانی دینامیکی دقیق در زمان و مکان خطی. هوشمند داده آنال. ۲۰۰۷ ، ۱۱ ، ۵۶۱-۵۸۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
یانگ، جی. ماریسکو-ایستودور، آر. Fränti، P. سه روش سریع برای میانگین‌گیری بخش‌های GPS. Appl. علمی ۲۰۱۹ ، ۹ ، ۴۸۹۹٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
تراسارتی، ر. گیدوتی، آر. مونریال، آ. Giannotti، F. Myway: پیش‌بینی مکان از طریق پروفایل تحرک. Inf. سیستم ۲۰۱۷ ، ۶۴ ، ۳۵۰-۳۶۷٫ [ Google Scholar ] [ CrossRef ]
ولاچوس، م. گونوپولوس، دی. کولیوس، جی. معیارهای تشابه قوی برای مسیرهای جسم متحرک. در مجموعه مقالات سیزدهمین کارگاه بین المللی IEEE در مورد پایگاه داده و برنامه های کاربردی سیستم های خبره (DEXA’02)، Aix-en-Provence، فرانسه، ۲-۶ سپتامبر ۲۰۰۲٫ صص ۷۲۱-۷۲۶٫ [ Google Scholar ]
چن، ال. اوزسو، MT; Oria، V. جستجوی شباهت قوی و سریع برای مسیر حرکت جسم متحرک. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2005 در مدیریت داده ها، بالتیمور، MD، ایالات متحده آمریکا، ۱۴-۱۶ ژوئن ۲۰۰۵٫ صص ۴۹۱-۵۰۲٫ [ Google Scholar ]
Rockafellar، TR; Wets، RJ-B. تجزیه و تحلیل متغیر ; Springer: برلین/هایدلبرگ، آلمان، ۲۰۰۹; جلد ۳۱۷٫ [ Google Scholar ]
چن، ال. Ng, R. در مورد ازدواج lp-هنجارها و فاصله ویرایش. در مجموعه مقالات سی امین کنفرانس بین المللی در مورد پایگاه های داده بسیار بزرگ، تورنتو، ON، کانادا، ۳۱ اوت تا ۳ سپتامبر ۲۰۰۴٫ جلد ۳۰، صص ۷۹۲–۸۰۳٫ [ Google Scholar ]
ژنگ، ی. ژو، X. محاسبات با مسیرهای فضایی . Springer Science & Business Media: برلین/هایدلبرگ، آلمان، ۲۰۱۱٫ [ Google Scholar ]
گرادشتاین، IS; Ryzhik, IM Tables of Integrals, Series, and Products , ۶th ed.; مطبوعات دانشگاهی: سن دیگو، کالیفرنیا، ایالات متحده آمریکا، ۲۰۰۰; صص ۱۱۱۴–۱۱۲۵٫ [ Google Scholar ]
ایتر، تی. Mannila، H. محاسبه فاصله فریشه گسسته. در گزارش فنی CD-TR 94/64 ; آزمایشگاه کریستین داپلر برای سیستم های خبره، TU وین: وین، اتریش، ۱۹۹۴; صص ۶۳۶-۶۳۷٫ [ Google Scholar ]
نی، پی. چن، ز. شیا، ن. هوانگ، Q. Li، F. تحلیل شباهت مسیر با وزن جهت و همسایگی k برای داده‌های AIS. ISPRS Int. J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۷۵۷٫ [ Google Scholar ] [ CrossRef ]
وانگ، اچ. سو، اچ. ژنگ، ک. صادق، س. ژو، ایکس. مطالعه اثربخشی بر روی معیارهای شباهت مسیر. در مجموعه مقالات بیست و چهارمین کنفرانس پایگاه داده استرالیا، آدلاید، استرالیا، ۲۹ ژانویه تا ۱ فوریه ۲۰۱۳٫ جلد ۱۳۷، ص ۱۳–۲۲٫ [ Google Scholar ]
یوجیان، ال. بو، L. یک متریک فاصله نرمال شده لونشتاین. IEEE Trans. الگوی مقعدی ماخ هوشمند ۲۰۰۷ ، ۲۹ ، ۱۰۹۱-۱۰۹۵٫ [ Google Scholar ] [ CrossRef ]
مولر، ام. تاب برداشتن زمان پویا. در بازیابی اطلاعات برای موسیقی و حرکت ; Springer: برلین/هایدلبرگ، آلمان، ۲۰۰۷; صص ۶۹-۸۴٫ [ Google Scholar ]
Huttenlocher، DP; کلندرمن، GA؛ راکلیج، WJ مقایسه تصاویر با استفاده از فاصله Hausdorff. IEEE Trans. الگوی مقعدی ماخ هوشمند ۱۹۹۳ ، ۱۵ ، ۸۵۰-۸۶۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
واگا، ک. Tabarcea، A. چن، ام. Fränti، P. تشخیص نوع حرکت با تقسیم بندی مسیر و طبقه بندی. در مجموعه مقالات هشتمین کنفرانس بین المللی محاسبات مشارکتی: شبکه، برنامه های کاربردی و اشتراک گذاری (CollaborateCom)، پیتسبورگ، PA، ایالات متحده آمریکا، ۱۴ تا ۱۷ اکتبر ۲۰۱۲٫ [ Google Scholar ]
چن، ام. خو، ام. Fränti، P. الگوریتم تقریب چند ضلعی چند ضلعی O(N) سریع برای ساده سازی مسیر GPS. IEEE Trans. فرآیند تصویر ۲۰۱۲ ، ۲۱ ، ۲۷۷۰-۲۷۸۵٫ [ Google Scholar ] [ CrossRef ]
ماریسکو-ایستودور، آر. Fränti, P. ورودی اشاره برای جستجوی مسیر GPS. در مجموعه مقالات کارگاه بین المللی مشترک در مورد شناسایی الگوی ساختاری، نحوی و آماری (S+SSPR 2016)، مریدا، مکزیک، ۲۹ نوامبر تا ۲ دسامبر ۲۰۱۶؛ صص ۴۳۹-۴۴۹٫ [ Google Scholar ]

شکل ۱٫ استخراج شبکه جاده از مسیرهای GPS به میانگین بخشی برای تبدیل مجموعه ای از مسیرهای بین دو تقاطع به یک بخش جاده نیاز دارد.

شکل ۲٫ میانگین گیری برای یافتن نمایندگانی برای خوشه های مسیر مورد نیاز است. این می تواند چالش برانگیز باشد زیرا مسیرها ممکن است اشکال پیچیده ای داشته باشند.

شکل ۳٫ نمونه هایی از استفاده از میانگین ( سمت چپ ) و medoid ( راست ) برای میانگین گیری بخش.

شکل ۴٫ ساختار کلی روش ها از رقابت میانگین گیری بخش [ ۷ ]. یک خط پایه جدید (نشان داده شده با آبی) با سنتز این روش ها ساخته شد.

شکل ۵٫ ساختار کلی الگوریتم RapSeg [ ۳۲ ] و ایجاد سه توصیفگر.

شکل ۶٫ اندازه گیری شباهت سلول سلسله مراتبی (HC-SIM) با جمع کردن مقادیر CSIM با استفاده از سطوح مختلف بزرگنمایی ساخته شده است. در مثال، این دو مسیر تنها یک مسیر انحرافی کوتاه دارند و تفاوت‌های جزئی فقط در متراکم‌ترین سطح زوم نشان داده می‌شوند. در بالاترین سطح زوم، منحنی ها یکسان در نظر گرفته می شوند.

شکل ۷٫ خلاصه ای از ابزارهای وب Mopsi در دسترس دیگران برای آزمایش میانگین گیری بخش و روش های مرتبط.

شکل ۸٫ هیستوگرام فرکانس امتیازها هنگام استفاده از HC-SIM (قرمز) و اقلیدسی (آبی).

شکل ۹٫ نمونه هایی از مجموعه های k مسیر (خطوط خاکستری) به طور میانگین توسط مدوید با فاصله DTW (خط آبی). خط سیاه حقیقت زمین است.

شکل ۱۰٫ نمونه های انتخاب شده از medoid با معیارهای تشابه HC-SIM و LCSS. خط آبی نتیجه متوسط است و خط سیاه حقیقت اصلی است.

شکل ۱۱٫ پیش پردازش مسیرها با نمونه برداری مجدد می تواند بر برخی از مسائل medoid غلبه کند. اندازه گیری LCSS در این نمونه ها استفاده شد. نمونه برداری مجدد (تا ۱۰ امتیاز) فقط برای میانگین بخش (خط آبی) نشان داده می شود.

شکل ۱۲٫ نمونه هایی که medoid امتیاز پایینی را با سه معیار فاصله با بهترین عملکرد ارائه می دهد. تعداد مسیرها در همه موارد بسیار کم است: k = ۳٫

شکل ۱۳٫ نتیجه ۱۰۰ مجموعه داده به عنوان تابعی از تعداد نقاط (مقیاس ورود) در مجموعه رسم شده است. نتایج مربوط به HC-SIM قبل از حذف موارد پرت ( بالا ) و HC-SIM بعد از حذف موارد پرت ( در زیر ) است. هر نقطه نشان دهنده یک مجموعه است و عدد نشان می دهد که چند مسیر در مجموعه وجود دارد.

شکل ۱۴٫ نتیجه ۱۰۰ مجموعه داده به عنوان تابعی از نقاط (مقیاس ورود) در مجموعه رسم شده است. نتایج برای DTW قبل از حذف نقاط پرت ( بالا ) و DTW بعد از حذف نقاط پرت ( زیر ) هستند. هر نقطه نشان دهنده یک مجموعه است و عدد نشان می دهد که چند مسیر در مجموعه وجود دارد.