AHP
AHP (فرایند تحلیل سلسله مراتبی) به عنوان یک روش برای MCDA توسعه داده شد که امکان بررسی انتقادی مفروضات اساسی، سازگاری قضاوتهای ارزشی را فراهم میکند و شناسایی مبادلات بین ملاحظات اجتماعی، اقتصادی و محیطی را برای طیف گستردهای از مشکلات تصمیمگیری تسهیل میکند (ساعتی). ۱۹۸۰). از سه اصل اساسی استفاده می کند : تجزیه، قضاوت مقایسه ای و سنتز.
تجزیه شامل شناسایی عناصر کلیدی یک مشکل تصمیم گیری، از جمله اهداف، معیارها و جایگزین ها، و ایجاد سلسله مراتب تصمیم گیری است. به عبارت دیگر، از آن برای ساختار مشکل تصمیم گیری استفاده می شود، مرحله دوم در روش کلی MCDA که در بالا مورد بحث قرار گرفت. ساختار سلسله مراتبی یک فعالیت نسبتاً ذهنی است که بر اساس تجربه و دانش تصمیم گیرندگان در مورد مشکل تصمیم گیری است. سلسله مراتب باید بر معیارهایی تمرکز کند که مهمترین آنها هستند. با توجه به ظرفیت محدود ذهن انسان برای مقایسه همزمان چیزها، AHP حداکثر ۵ تا ۹ شاخه را در هر گره در سلسله مراتب تصمیم گیری می خواهد تا کارایی و ثبات زیادی در ارزیابی داشته باشد.
بر اساس سلسله مراتب، اصل قضاوت های مقایسه ای برای تعیین اهمیت نسبی معیارها و ترجیح نسبی گزینه ها از طریق مقایسه های زوجی اعمال می شود. عناصر در یک سطح معین در یک سلسله مراتب به صورت جفت با توجه به یک ویژگی یا معیار مشترک در سطح بالا مقایسه می شوند. AHP از مقیاس اساسی اعداد مطلق برای بیان ترجیحات یا قضاوت های فردی استفاده می کند. جدول ۹-۲ این مقادیر مقیاس اساسی را فهرست می کند. اگر افراد زیادی شرکت کنند، قضاوت های متعدد را می توان با استفاده از ابزارهای هندسی قضاوت های فردی ترکیب کرد. قضاوتهای مقایسه ای باید بر اساس بهترین اطلاعات موجود و شهود، دانش و تجربه تصمیم گیرندگان انجام شود.
مقایسات زوجی در برابر معیار یا ویژگی معین منجر به ماتریس می شود. جدول ۹-۳ ماتریسی از مقایسه جفتی معیارها را با توجه به هدف کلی در نشان می دهد. شکل ۹-۱ به اعداد موجود در ماتریس مقادیر مقیاس AHP هستند که تعاریف آنها در آن شرح داده شده است. در جدول ۹-۲ آنها با احکام بدست آمده از مقایسه عناصر ستون سمت چپ با عناصر ردیف بالا مطابقت دارند. وقتی عنصری کمتر از عنصر دیگر مورد توجه قرار گیرد، قضاوت کسری است. می توان توجه داشت که هنگام مقایسه یک عنصر با خود، مقایسه باید ۱ باشد.
بنابراین مقادیر مورب ماتریس مقایسه زوجی همیشه ۱ است. ماتریس مقایسه زوجی نیز متقابل است. قضاوت فقط برای قسمت مثلثی بالایی یک ماتریس مورد نیاز است. قسمت مثلثی پایینی متقابل آنهاست. هنگامی که یک ماتریس مقایسه زوجی ایجاد شد، AHP وزن ها یا اولویت های عناصر مربوطه را با حل بردار ویژه اصلی ماتریس استخراج می کند. فرض کنید عناصر C1, C2, . . . ، Cn در سطحی از سلسله مراتب هستند، می خواهیم وزن اولویت آنها را پیدا کنیم، w1، w2، . . ., wn. مقدار wi نشان دهنده درجه تأثیر یا اهمیت Ci با توجه به عنصر معیار در سطح بالا است. ما از aij برای نشان دادن مقدار مقایسه جفتی Ci نسبت به Cj استفاده می کنیم. ماتریس مقایسه جفتی برای این عناصر به صورت زیر نشان داده شده است :

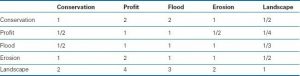
جدول ۹-۳ ماتریس مقایسه زوجی
به دست آوردن وزن های بر اساس A مسئله مقدار ویژه است :

که در اینجا λmax بزرگترین یا اصلی ترین ارزش ویژه A است. راه حل w با بالا بردن ماتریس به قدر کافی بزرگ، سپس جمع آوری سطرها و عادی سازی بدست می آید. وزنهای حاصل از ماتریس مقایسه زوجی با توجه به یک معیار خاص، وزنهای محلی نامیده میشوند. پس از وزن دهی به عنصر ملاک، وزن جهانی نامیده می شود. بعد از اینکه همه قضاوت ها انجام شد و همه ماتریس های مقایسه زوجی بدست آمدند، وزن جهانی عناصر محاسبه می شود. با پایین آمدن سلسله مراتب از سطح دوم، وزن کلی برای هر عنصر در سطحی با ضرب وزن محلی آن در اولویت های عناصر معیار در سطح بلافاصله بالا و اضافه کردن آنها محاسبه می شود. این وزن جهانی به نوبه خود برای وزن دهی وزن های محلی عناصر مربوطه در سطح پایین و غیره به سطح پایین استفاده می شود. این فرآیند در AHP سنتز نامیده می شود که منجر به مجموعه ای از اولویت های کلی برای گزینه های موجود در سطح پایین می شود. جزئیات سنتز و نتایج کلی برای مشکل تصمیم گیری مدیریت پوشش گیاهی ساحلی در شکل ۹-۲ نشان داده شده است.
AHP همچنین ناسازگاری قضاوت ها را اندازه گیری می کند. گفته می شود ماتریس مقایسه جفتی A اگر کاملاً سازگار باشد
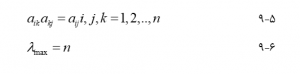
هرچه λmax به n نزدیکتر باشد ، قضاوت ها سازگارتر هستند. شاخص ثبات در AHP به شرح زیر تعریف شده است :

به منظور به دست آوردن تفسیر معنی دار از شاخص سازگاری، ساعتی (۱۹۸۰) نسبت ثبات را که نسبت ناسازگاری نیز نامیده می شود، به عنوان نسبت شاخص سازگاری برای مجموعه ای از قضاوت ها به میانگین شاخص ثبات برای مقایسه های تصادفی برای ماتریس با همان اندازه مجموعه ای از قضاوت های کاملاً سازگار، نسبت ناسازگاری صفر را ایجاد می کند، در حالی که مجموعه ای از قضاوت های ناسازگار معادل آنچه از قضاوت های تصادفی انتظار می رود، نسبت ناسازگاری ۱ را تولید می کند. به عنوان یک قاعده کلی، هنگامی که نسبت ناسازگاری بیش از ۱/۰باشد، قضاوت ها اغلب نیاز به بررسی مجدد دارند.
مطالعه موردی ۵ در فصل ۱۰ شامل استفاده از AHP در ارزیابی زمین در شمال لائوس در امتداد مرز با چین است.
