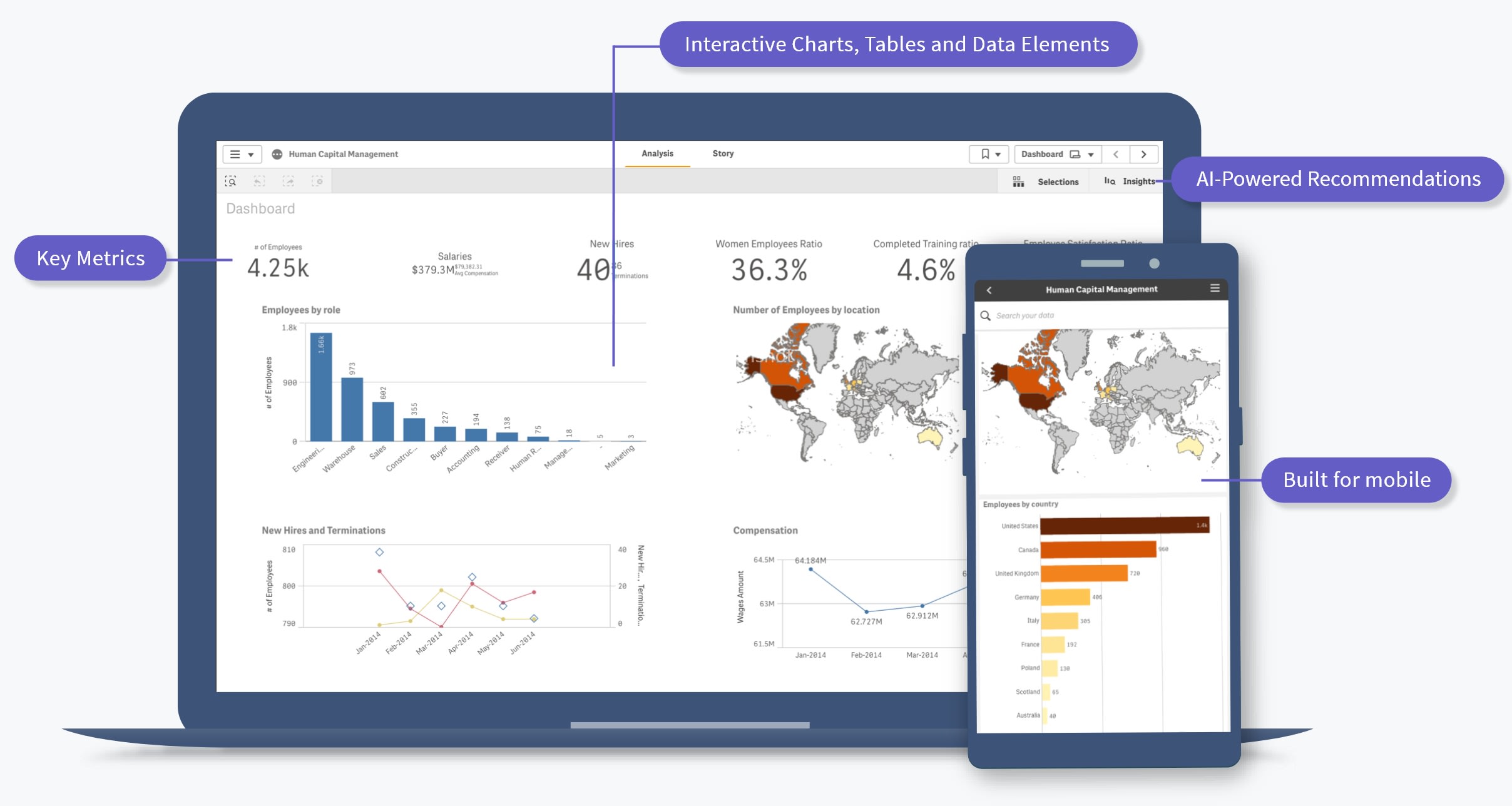
ویژگی های داده و تجسم
در پست های قبلی، آموختیم که چگونه بستههای نرمافزاری سیستم اطلاعات جغرافیایی (GIS) از پایگاههای داده برای ذخیرهسازی اطلاعات ویژگیهای مختلف اطلاعات مکانی در یک نقشه استفاده میکنند. با این حال، ارزش واقعی این اطلاعات زمانی مشخص میشود که ابزارهای تحلیلی قدرتمند مشابهی برای دسترسی، پردازش و سادهسازی دادهها به کار گرفته شوند. برای این منظور، GIS معمولاً مجموعهای از ابزارهای پیشرفته برای جستجو، پرسوجو، توصیف، خلاصهسازی و طبقهبندی دادهها ارائه میدهد. با استفاده از این ابزارها، حتی بزرگترین مجموعههای داده نیز قابل استخراج هستند تا به کاربران این امکان را بدهند که بینشهای معنیداری از آن اطلاعات استخراج کرده و تحلیلهایی مفید ارائه دهند.
توضیحات و خلاصه
هدف یادگیری
هدف این بخش، بررسی رایجترین معیارهای توزیع، تمایل مرکزی و پراکندگی است.
هیچ بحثی در مورد تجزیه و تحلیل جغرافیایی بدون مروری مختصر بر مفاهیم اولیه آماری کامل نخواهد بود. آمارهای اساسی معرفیشده در اینجا، نقطه شروعی برای هر تلاشی در جهت توصیف، خلاصهسازی و تحلیل مجموعههای داده جغرافیایی هستند. نمونهای از تلاشهای آماری در زمینفضا، تجزیه و تحلیل دادههای نقطهای بهدستآمده از مجموعهای از سنجش های بارندگی است که در سراسر یک منطقه خاص توزیع شدهاند. با استفاده از این بارانسنجها، میتوان مقدار معمولی و تغییرپذیری بارندگی در هر ایستگاه را محاسبه کرده و همچنین میزان بارندگی متوسط در سطح کل منطقه را تعیین کرد. علاوه بر این، میتوان میزان بارندگی را بین هر ایستگاه یا در مناطقی که بیشترین یا کمترین بارندگی رخ میدهد، درونیابی کرد. همچنین، میتوان مقدار پیشبینی شده بارندگی را در آینده برای هر ایستگاه یا بین ایستگاهها پیشبینی نمود.
افزایش قدرت محاسباتی در چند دهه گذشته باعث تولید مجموعه دادههای گستردهای شده است که جمعبندی آنها بهسادگی امکانپذیر نیست. آمار توصیفی، توصیفات عددی سادهای از این مجموعه دادههای بزرگ ارائه میدهد. آمار توصیفی عمدتاً به تحلیل تکمتغیره میپردازد، به این معنا که یک متغیر را در یک زمان بررسی میکند. سه دسته اصلی از آمار توصیفی وجود دارند که در اینجا به آنها پرداخته خواهد شد: معیارهای توزیع، معیارهای گرایش مرکزی و معیارهای پراکندگی. با این حال، پیش از اینکه به تفصیل به تکنیکهای آماری مختلف پرداخته شود، ابتدا باید چند اصطلاح پایه را تعریف کنیم:
-
- متغیر: نمادی که برای نشان دادن هر مقدار یا مجموعهای از مقادیر استفاده میشود.
- مقدار: مشاهده فردی از یک متغیر (در سیستم اطلاعات جغرافیایی [GIS] به آن رکورد نیز گفته میشود).
- جمعیت: مجموعهای از تمام مقادیر ممکن برای یک متغیر.
- نمونه: زیرمجموعهای از جمعیت.
- n: تعداد مشاهدات یک متغیر.
- آرایه: دنبالهای از مقادیر مشاهده شده (در GIS به آن فیلد نیز گفته میشود و در جدول ویژگیها به صورت ستون نمایش داده میشود).
- آرایه مرتبشده: یک آرایه مرتبشده و کمی.
اقدامات توزیع
اندازهگیری توزیع یک متغیر، صرفاً خلاصهای از فراوانی مقادیر در دامنه مجموعه داده است (که به آن توزیع فراوانی نیز گفته میشود). به طور معمول، مقادیر متغیر دادهشده در یک سری از کلاسهای از پیش تعیینشده (که به آنها فواصل، بنها یا دستهها نیز گفته میشود) گروهبندی میشوند و تعداد مقادیر دادهای که در هر کلاس قرار میگیرند، خلاصه میشود. نموداری که تعداد مقادیر داده را در هر کلاس نشان میدهد، هیستوگرام نامیده میشود.
برای مثال، درصد نمرات یک کلاس در یک امتحان ممکن است به آرایه زیر منجر شود (n = 30):
آرایه نمرات امتحان: {۸۷، ۷۶، ۸۹، ۹۰، ۶۴، ۶۷، ۵۹، ۷۹، ۸۸، ۷۴، ۷۲، ۹۹، ۸۱، ۷۷، ۷۵، ۸۶، ۹۴، ۶۶، ۷۵، ۷۴، ۸۳، ۹۲، ۷۵، ۷۳، ۷۰، ۶۰، ۸۰، ۸۵، ۵۷}
برای قرار دادن این آرایه در یک توزیع فراوانی، دستورالعملهای کلی زیر باید رعایت شوند:
- بین پنج تا پانزده کلاس مختلف باید استفاده شوند، اگرچه تعداد دقیق کلاسها به تعداد مشاهدات بستگی دارد.
- هر مشاهده باید به یک و تنها یک کلاس اختصاص یابد.
- در صورت امکان، از کلاسهایی استفاده شود که مقادیرشان در محدودههای مساوی تقسیمبندی شدهاند (فروند و پرلز، ۲۰۰۶).
با رعایت این رهنمودها، آرایه نمرات امتحانی که پیشتر نشان داده شد، میتواند به شکل هیستوگرام زیر تجسم شود (شکل ۶٫۱ “هیستوگرام نشاندهنده توزیع فراوانی نمرات امتحان”).
شکل ۶٫۱ هیستوگرام توزیع فراوانی نمرات امتحان را نشان می دهد

همانطور که از هیستوگرام مشاهده میشود، میتوان مشاهدات توصیفی خاصی را بهراحتی انجام داد. بیشتر دانشآموزان در امتحان نمره C (70-79) دریافت کردهاند. دو دانشآموز در امتحان مردود شدهاند (۵۰-۵۹). پنج دانشآموز نمره A (90-99) کسب کردهاند. توجه داشته باشید که این هیستوگرام سومین قانون اساسی را نقض میکند که بر اساس آن هر کلاس باید محدوده مساوی داشته باشد، زیرا محدوده نمرات F (0-59) متغیر است، در حالی که سایر درجات محدودههایی با اندازه یکسان دارند. با این حال، در این مورد، نگرانی اصلی ما توصیف توزیع نمرات امتحانی است. بنابراین، ایجاد محدودههای کلاسی که بهترین تطابق را با نیازهای خاص ما دارند، کاملاً منطقی به نظر میرسد.
اقدامات گرایش مرکزی
ما میتوانیم آرایه نمرات امتحان را با اعمال معیارهای گرایش مرکزی بیشتر بررسی کنیم. سه معیار اصلی برای گرایش مرکزی وجود دارد: میانگین، حالت و میانه.
میانگین که معمولاً بهعنوان «میانگین حسابی» شناخته میشود، بیشترین استفاده را برای سنجش گرایش مرکزی دارد. برای محاسبه میانگین، کافی است تمام مقادیر موجود در آرایه را جمع کرده و آن مجموع را بر تعداد مشاهدات تقسیم کنید. برای بازگشت به مثال نمرات امتحان قبلی، مجموع آن آرایه ۲۳۴۰ است و تعداد مشاهدات ۳۰ (n = 30) میباشد. بنابراین، میانگین برابر با ۲۳۴۰ ÷ ۳۰ = ۷۸ است.
حالت معیاری است که بیشترین فراوانی را در آرایه نشان میدهد. در مورد نمرات امتحان، حالت برابر با ۷۵ است، زیرا بیشترین تعداد دانشآموزان (در مجموع سه نفر) این نمره را دریافت کردهاند.
میانه به مشاهدهای گفته میشود که وقتی آرایه از کمترین به بیشترین مرتب میشود، دقیقاً در وسط آن قرار میگیرد. بهطور خاص، میانه مقداری است که در وسط آرایه مرتبشده زمانی که تعداد مشاهدات فرد باشد، قرار دارد. از طرف دیگر، هنگامی که تعداد مشاهدات زوج باشد، میانه با یافتن میانگین دو مقدار مرکزی محاسبه میشود. اگر آرایه نمرات امتحان را مجدداً مرتب کنیم، نمرات به این ترتیب فهرست میشوند:
آرایه مرتبشده از نمرات امتحان: {۵۷، ۵۹، ۶۰، ۶۴، ۶۶، ۶۷، ۷۰، ۷۲، ۷۳، ۷۴، ۷۴، ۷۵، ۷۵، ۷۵، ۷۶، ۷۷، ۷۹، ۸۰، ۸۱، ۸۳، ۸۵، ۸۶، ۸۷، ۸۸، ۸۹، ۹۰، ۹۲، ۹۳، ۹۴، ۹۹}
از آنجا که در این مثال تعداد مشاهدات برابر با ۳۰ (n = 30) است، تعداد مشاهدات زوجی داریم. بنابراین، برای محاسبه میانه، میانگین دو مقدار مرکزی (مقدار ۱۵ام = ۷۶ و مقدار ۱۶ام = ۷۷) محاسبه میشود که در نتیجه میانه برابر با (۷۶ + ۷۷) ÷ ۲ = ۷۶٫۵ خواهد بود.
در مجموع، میانگین، حالت و میانه ابتداییترین راهها برای تحلیل روندها در یک مجموعه داده هستند.
اقدامات پراکندگی
سومین نوع آمار توصیفی، معیارهای پراکندگی است (که به آنها معیارهای تغییرپذیری نیز گفته میشود). این معیارها پراکندگی دادهها را در اطراف میانگین توصیف میکنند. سادهترین معیار پراکندگی، محدوده است که برابر با تفاوت بزرگترین مقدار و کوچکترین مقدار در مجموعه دادهها است. در مثال ما، محدوده برابر با ۹۹−۵۷=۴۲۹۹ – ۵۷ = ۴۲ است.
محدوده بین چارکی معیاری پیچیدهتر برای اندازهگیری پراکندگی است. این روش دادهها را به چهار بخش تقسیم میکند. برای انجام این کار، ابتدا از میانه برای تقسیم آرایه مرتبشده به دو نیمه استفاده میشود. سپس این نیمهها دوباره با استفاده از میانه خود به دو بخش تقسیم میشوند. چارک اول (Q1) میانه نیمه پایینی آرایه مرتبشده است و بهعنوان چارک پایین نیز شناخته میشود. Q2 همان میانه کل آرایه است. Q3 میانه نیمه بالایی آرایه مرتبشده است و بهعنوان چارک بالا شناخته میشود. تفاوت بین چارک بالا و پایین، محدوده بین چارکی را تشکیل میدهد. در مثال نمرات امتحان، Q1=72.25Q1 = 72.25 و Q3=86.75Q3 = 86.75 است. بنابراین، محدوده بین چارکی برای این مجموعه داده ۸۶٫۷۵−۷۲٫۲۵=۱۴٫۵۰۸۶٫۷۵ – ۷۲٫۲۵ = ۱۴٫۵۰ است.
واریانس (که معمولاً با نماد s2s^2 نمایش داده میشود) سومین معیار پراکندگی است. برای محاسبه واریانس، باید هر نمره امتحان را از میانگین نمرات امتحان کم کنید. همانطور که ممکن است حدس بزنید، برخی از تفاوتها مثبت و برخی منفی خواهند بود که در نتیجه مجموع این تفاوتها برابر با صفر میشود. از آنجایی که بیشتر به بزرگی این تفاوتها (یا انحرافات) از میانگین علاقهمندیم، یک روش برای غلبه بر این ویژگی “صفر شدن” آنها، مربع کردن هر انحراف است. اینگونه مقادیر منفی از محاسبات حذف میشوند (شکل ۶٫۲). این کار منجر به موارد زیر میشود:
شکل ۶٫۲

سپس مجموع مربعات انحرافات را بر n−۱n – 1 (در صورتی که با نمونه کار میکنیم) یا nn (در صورتی که با جمعیت کامل کار میکنیم) تقسیم میکنیم. از آنجایی که نمرات امتحان دادهشده در اینجا نمایانگر کل جمعیت کلاس است، از فرمول واریانس استفاده میکنیم که منجر به واریانس s2=116.4s^2 = 116.4 میشود. اگر بخواهیم از این نمرات امتحانی برای برونیابی اطلاعات در مورد جمعیت بزرگتر استفاده کنیم، با نمونهای از جامعه کار خواهیم کرد و در این صورت مجموع مربعات انحرافات را بر n−۱n – 1 تقسیم میکنیم.
شکل ۶٫۳ واریانس

انحراف استاندارد، که آخرین و رایجترین معیار پراکندگی است که در اینجا بررسی میشود، برای جبران تأثیر مربع کردن هر تفاوت از میانگین در محاسبه واریانس، جذر واریانس را میگیرد. همانطور که در شکل ۶٫۴ “انحراف استاندارد” نشان داده شده است، در مثال نمرات امتحان، انحراف استاندارد برابر با s=116.4=10.8s = \sqrt{116.4} = 10.8 است.
شکل ۶٫۴ انحراف معیار

محاسبه انحراف استاندارد به ما این امکان را میدهد که استنباطهای معناداری در مورد پراکندگی مجموعه دادههای خود داشته باشیم. انحراف استاندارد کوچک نشاندهنده این است که مقادیر مجموعه داده بهطور متمرکز در اطراف میانگین جمع شدهاند، در حالی که انحراف استاندارد بزرگتر نشاندهنده پراکندگی وسیع مقادیر در اطراف میانگین است.
اگر مجموعه داده با توزیع نرمال مطابقت داشته باشد، میتوان استنباطهای بیشتری در مورد انحراف استاندارد انجام داد. توزیع نرمال به این معناست که دادهها، وقتی در یک توزیع فرکانس (هیستوگرام) قرار میگیرند، متقارن و بهطور کلی “زنگشکل” به نظر میرسند. در غیر این صورت، توزیع دادهها به طور مثبت یا منفی “منحرف” یا “مائل” نامیده میشود (شکل ۶٫۵ “هیستوگرام مجموعه دادههای منحنی، با انحراف مثبت و منفی”). دادههای مایل، دادههایی هستند که حول میانگین بهطور متقارن توزیع نشدهاند.
با این حال، دادههای با توزیع نرمال این ویژگی را دارند که تقریباً ۶۸ درصد از مقادیر دادهها در یک انحراف استاندارد ±۱ از میانگین قرار میگیرند و ۹۵ درصد از مقادیر دادهها در یک انحراف استاندارد ±۲ از میانگین قرار دارند. در مثال ما، با میانگین ۷۸ و انحراف استاندارد ۱۰٫۸، میتوان گفت که ۶۸ درصد از نمرات در بازه ۶۷٫۲ تا ۸۸٫۸ (یعنی ۷۸ ± ۱۰٫۸) قرار دارند، در حالی که ۹۵ درصد از نمرات در بازه ۵۶٫۴ تا ۹۹٫۶ قرار دارند (یعنی ۷۸ ± [۱۰٫۸ * ۲]).
برای مجموعه دادههایی که با منحنی نرمال مطابقت ندارند، میتوان فرض کرد که حدود ۷۵ درصد از مقادیر دادهها در بازه ±۲ انحراف استاندارد از میانگین قرار دارند.
شکل ۶٫۵ هیستوگرام مجموعه داده های منحنی معمولی، دارای انحراف مثبت و منحنی منفی

خوراکی های کلیدی
- اندازه گیری توزیع برای یک متغیر معین خلاصه ای از فراوانی مقادیر در محدوده مجموعه داده است و معمولاً با استفاده از یک هیستوگرام نشان داده می شود.
- اندازهگیریهای گرایش مرکزی تلاش میکنند تا بینشهایی را درباره ارزش «معمولی» برای یک مجموعه داده ارائه دهند.
- معیارهای پراکندگی (یا تغییرپذیری) پراکندگی داده ها در اطراف میانگین یا میانه را توصیف می کند.
تمرینات
- یک جدول حاوی حداقل سی مقدار داده ایجاد کنید.
- برای جدولی که ایجاد کردید، میانگین، حالت، میانه، محدوده، محدوده بین چارکی، واریانس و انحراف معیار را محاسبه کنید.