مشاوره رایگان
فیس بوکتوئیتراینستاگراماسکایپ
کپی رایت 2024

حسابداری برای تنوع زمین شناسی محلی در شبیه سازی های متوالی – مفهوم و کاربرد

مقالات حسابداری برای تنوع زمین شناسی محلی در شبیه سازی های متوالی - مفهوم و کاربرد

خلاصه

مدل‌های ویژگی حفظ ناهمگونی مناطق زیرسطحی معمولاً با استفاده از شبیه‌سازی‌های متوالی ساخته می‌شوند. شبیه‌سازی گاوسی متوالی (SGS) و شبیه‌سازی متوالی مستقیم (DSS) مقادیری را از یک تابع چگالی احتمال محلی می‌گیرند که با تخمین کریجینگ ساده و واریانس کریجینگ ساده محلی در مکان‌های نمونه‌گیری نشده توصیف می‌شود. با این حال، واریانس کریجینگ ساده محلی لزوماً منعکس کننده تنوع زمین شناسی موجود در زیر مجموعه های حوزه هدف نیست. به منظور پرداختن به این مشکل، یک گردش کار جدید را پیشنهاد می کنیم که دو نسخه اصلاح شده از الگوریتم های محبوب SGS و DSS را پیاده سازی می کند. هر دو اصلاح، یعنی LVM-DSS و LVM-SGS، با هدف شبیه سازی مقادیر با استفاده از یک مدل واریانس محلی (LVM) هستند. LVM یک نمایش جهانی محدود و مبتنی بر زمین شناسی از واریانس قابل مشاهده محلی یک ویژگی است. الگوریتم‌های اصلاح‌شده پیشنهادی، تابع چگالی احتمال محلی را با LVM به‌جای استفاده از واریانس کریجینگ ساده می‌سازند، در حالی که هنوز از تخمین کریجینگ ساده به‌عنوان بهترین برآوردگر خطی بی‌طرف استفاده می‌کنند. در یک مطالعه آنالوگ رخنمون، می‌توانیم نشان دهیم که واریانس کریجینگ ساده محلی در شبیه‌سازی‌های متوالی تمایل به دست کم گرفتن تغییرپذیری زمین‌شناسی مشاهده شده محلی در حوزه هدف دارد و مطمئناً توزیع فضایی ناهمگونی زمین‌شناسی را در نظر نمی‌گیرد. الگوریتم های شبیه سازی پیشنهادی هیستوگرام جهانی، ناهمگنی جهانی و مدل واریوگرام در نظر گرفته شده را در محدوده نوسانات ارگودیک بازتولید می کنند. LVM-SGS نسبت به الگوریتم های دیگر در مورد بازتولید مدل واریوگرام بهتر عمل می کند. در حالی که DSS و SGS یک ناهمگنی توزیع شده تصادفی ایجاد می کنند، الگوریتم های اصلاح شده به جای آن یک توزیع فضایی منطقی از نظر زمین شناسی ناهمگنی را تولید می کنند. گردش کار جدید امکان ادغام روندهای زمین شناسی پیوسته را در شبیه سازی های متوالی به جای استفاده از رویکردهای کلاس محور مانند تکنیک شبیه سازی نشانگر فراهم می کند.

کلید واژه ها:

شبیه سازی متوالی ; مدل واریانس محلی ; ناهمگونی زمین شناسی ; تخمین عدم قطعیت ; تنوع زیر مجموعه

۱٫ معرفی

نتیجه گیری از داده های نامطمئن در علوم زمین بسیار معمول است تا غیر معمول. هر اندازه گیری در مطالعات زمین شناسی متاثر از خطاهای اندازه گیری است و تنها زیر مجموعه ای از تنوع طبیعی رسانه های زمین شناسی را نشان می دهد. تنوع طبیعی یک عامل کنترل کننده مهم تجاری برای انواع مختلف بهره برداری زیرسطحی مانند استخراج، بهره برداری هیدروکربن و زمین گرمایی، جذب و ذخیره کربن، یا دفع زباله های هسته ای است. تنوع فیزیکی سنگ ها به عنوان پیچیدگی یا ناهمگونی یک سیستم در زمان و مکان تعریف می شود [ ۱ ]. حتی اختلافات حاشیه ای از توزیع اموال پیش بینی شده در سطح زیرزمینی می تواند منجر به شبیه سازی نادرست پتانسیل تولید معدن یا بازیابی و طول عمر یک مخزن شود.۲ ، ۳ ]. به خصوص تنوع در مقیاس کوچک خواص فیزیکی سنگ، پیش‌بینی‌های اندازه میدان را همچنان چالش برانگیز می‌کند.
ناهمگونی طبیعی و توزیع ویژگی مربوطه در زمان و مکان را می توان از طریق درون یابی، رگرسیون آماری، یادگیری ماشینی یا شبیه سازی تصادفی [ ۴ ، ۵ ] با استفاده از تعدادی مشاهدات یا داده های آموزشی مدل کرد. به دلیل محدودیت‌های فنی، اقتصادی یا زمانی، کمپین‌های نمونه‌گیری زمین‌شناسی عملاً همیشه به مجموعه داده‌های کمیاب در یک دامنه هدف ختم می‌شوند.  Ω. بر این اساس، برآورد خواص اغلب ساختارهای زمین‌شناسی مشاهده‌شده در میدان را در نظر نمی‌گیرد یا نادرست است و به‌ویژه تکنیک‌های درون‌یابی مرسوم مانند کریجینگ، انتقال‌های صاف در مرزهای زمین‌شناسی تیز ایجاد می‌کنند. علاوه بر این، آنها ممکن است نتوانند آمار جهانی را به درستی تولید کنند. درون یابی های مرسوم تمایل به دست کم گرفتن حضور مقادیر در دم بالایی یک توزیع و به همین ترتیب در دم پایینی نیز دارند [ ۵ ]. در نتیجه، ناهمگونی‌های زمین‌شناسی عمده، مانند گسل‌ها، سطوح مرزی اصلی، یا ناهنجاری‌های فیزیکوشیمیایی، به احتمال زیاد توسط یک تابع تصادفی پیوسته (RF) بازتولید نمی‌شوند [ ۶ ].
برخلاف تکنیک‌های درون‌یابی مرسوم، شبیه‌سازی‌های تصادفی با هدف بازتولید واریانس و هیستوگرام مشاهده‌شده در داده‌های جهانی [ ۷ ، ۸ ] انجام می‌شود. بر اساس محدود بودن یا نبودن، شبیه‌سازی‌های تصادفی به شبیه‌سازی‌های غیرشرطی و شرطی تقسیم می‌شوند [ ۹ ]]. شبیه‌سازی‌های بی‌قید و شرط مبتنی بر مونت کارلو، هیستوگرام اصلی را بدون محدودیت‌های مکانی بازتولید می‌کنند. با این حال، تحقق‌هایی که توسط آن روش‌ها ایجاد می‌شود، به طور منظم از نمایش توزیع فضایی واقعی دور هستند و در بهترین حالت «به احتمال زیاد» موارد را تشکیل می‌دهند. در مقابل، شبیه‌سازی‌های شرطی با هدف بازتولید توزیع ویژگی اصلی با استفاده از نقاط نمونه‌گیری گسسته همراه با ویژگی‌های فضایی مانند مدل واریوگرام مشاهده‌شده [ ۱۰ ].
یکی از انواع الگوریتم‌های شبیه‌سازی مرسوم با شبیه‌سازی گاوسی متوالی (SGS) نشان داده می‌شود که در آن تغییرپذیری محلی با نمونه‌برداری از تابع چگالی احتمال محلی (PDF) مشتق‌شده از واریانس کریجینگ ساده محلی شبیه‌سازی می‌شود. σاسک۲. این پارامتر از درون یابی قبلی انجام شده از مجموعه داده استاندارد توزیع شده [ ۱۱ ] حاصل می شود. مطالعات میدانی اولیه پتانسیل این روش را برای پیش‌بینی ویژگی‌های سنگ در مکان‌های ناشناخته و ارزیابی عدم قطعیتی که می‌توان در ناحیه مورد نظر انتظار داشت، اثبات کرده است [ ۱۲ ، ۱۳ ، ۱۴ ، ۱۵ ]. رویکردهای جدیدتر منجر به تغییراتی در الگوریتم SGS بدون نیاز به تبدیل متغیر اصلی به فضای عادی استاندارد می شود. این تکنیک – که بهتر به عنوان شبیه‌سازی‌های متوالی مستقیم (DSS) شناخته می‌شود – ممکن است برای مثال از هیستوگرام سراسری نمونه برداری کند تا از PDF محلی [ ۹ ]] یا پس از شبیه سازی، یک تبدیل چندک به فضای متغیر اصلی انجام دهید. این رویکردها می‌توانند هم هیستوگرام اصلی و هم مدل نیم‌واریوگرام تجربی را بازتولید کنند [ ۱۰ ]. PDF محلی مشتق شده از σاسک۲با این حال، عمدتاً منعکس کننده درجه عدم قطعیت ناشی از خود روش درونیابی است و لزوماً منعکس کننده تغییرپذیری محلی مشاهده شده در مقیاس کوچکتر از Ω.
به منظور افزایش دقت شبیه‌سازی‌های متوالی، ما یک گردش کار جدید را پیشنهاد می‌کنیم که تنوع محلی حاصل از اندازه‌گیری‌ها را در زیرمجموعه‌ای از Ωبه SGS و DSS با در نظر گرفتن خطاهای اندازه گیری. الگوریتم‌های SGS و DSS اصلاح‌شده از یک نمایش کلی از واریانس قابل مشاهده محلی، به نام مدل واریانس محلی (LVM) استفاده می‌کنند تا یک مقدار را در یک مکان نمونه‌برداری نشده ترسیم کنند. بر این اساس، الگوریتم ها LVM-SGS و LVM-DSS نامیده می شوند. قبل از شبیه‌سازی، یک تحلیل بهینه‌سازی برنامه‌نویسی عدد صحیح به منظور بهینه‌سازی استحکام تابع درونیابی زیربنایی انجام می‌شود. به جای نمونه برداری از PDF محلی، که با استفاده از σاسک۲، یا با حل یک مشکل بهینه سازی جهانی، رویکرد پارامتریک ما یک PDF محلی را بر اساس واریانس محدود شده با اندازه گیری و زمین شناسی استخراج شده از LVM شبیه سازی می کند. PDF محلی بدین وسیله با تبدیل Box-Muller [ ۱۶ ] شبیه سازی شده است.
این روش در یک مطالعه موردی، که در یک تشکیل مخزن زمین گرمایی بالقوه در جنوب غربی آلمان انجام شده است، آزمایش و تایید شد. بنابراین، ما نفوذپذیری ذاتی را که یک پارامتر کلیدی در بسیاری از انواع بهره‌برداری زیرسطحی است، روی مجموعه‌ای از نمونه‌های گرفته‌شده از یک معدن فعال اندازه‌گیری کردیم. Ωتوسط یک مدل رخنمون ۳ بعدی نشان داده شده است که با استفاده از بازسازی دیوار رخنمون فتوگرامتری ساخته شده است. این مدل ۹۰۰۰ متر حجم را پوشش می دهد ۳. تنوع در مقیاس کوچک از نمونه های سنگی که از دو مکعب سنگ نماینده گرفته شده است، به دست می آید. آنها به عنوان Ωبو حجم ۰٫۰۱۵۶ متر را پوشش می دهد ۳و ۰٫۰۰۸ متر ۳، به ترتیب. مکعب های سنگ از همان رخنمون گرفته شده اند که نمونه های جهانی از آن گرفته شده است. در نهایت، رویکرد ما با الگوریتم‌های معمولی SGS و DSS مقایسه شده و با توانایی آن در بازتولید مدل واریوگرام جهانی و ناهمگنی زمین‌شناسی ارزیابی می‌شود.

۲٫ پیشینه نظری

۲٫۱٫ تغییرپذیری فضایی

به منظور کاهش احتمال شکست اقتصادی در صنایع معدنی، مفهوم متغیر منطقه‌ای شده توسط Matheron [ ۱۷ ] در دهه ۱۹۶۰ ایجاد شد. متغیر منطقه ای تابعی است که در هر نقطه از فضا مقدار معینی می گیرد. در رسانه‌های زمین‌شناسی، آن متغیر منطقه‌ای شده اغلب پیچیده‌تر از آن است که بتوان آن را با توابع ریاضی بیان کرد. یک متغیر منطقه‌ای شده فرض می‌شود که تداوم کم و بیش ثابتی در فضا همراه با نوسانات محلی را نشان می‌دهد ( شکل ۱ ). در رسانه های زمین شناسی، این نوسانات معمولاً ناشی از تنوع فیزیکی مشاهده شده در مقیاس های کوچکتر است.

تنوع سنگ شناسی و فیزیکی موضوع مطالعات زمین شناسی متعددی است [ ۱۸ ، ۱۹ ، ۲۰ ، ۲۱ ] و معمولاً ناهمگنی نامیده می شود . در فرهنگ لغت آکسفورد [ ۲۲ ] واژه ناهمگونی به عنوان تفاوت یا تنوع در نوع از چیزهای دیگر یا ترکیبی از عناصر یا اجزای متنوع تعریف شده است. ترکیب چندگانه . در بیشتر آثار، این اصطلاح برای توصیف اینکه یک شی شامل چندین زیرمجموعه است که در یک یا چند ویژگی با یکدیگر متفاوت هستند، استفاده می شود. لی و رینولدز [ ۱] عبارت را به تغییرپذیری ویژگی سیستم در فضای سه بعدی محدود می کند. فیچ و همکاران [ ۲۳ ] مجموعه‌ای از روش‌ها را برای تعیین کمیت ناهمگنی در نمونه‌ای از مشاهدات از جمله ضریب تغییرات ارائه می‌کند. جv)

جv=σ۲μ،

جایی که σانحراف معیار است و μمیانگین حسابی و ضریب Dykstra–Parsons است ( جدپ)

جدپ=ایکس۵۰-ایکس۸۴ایکس۵۰،

جایی که ایکسnصدک n یک توزیع است.

بنابراین تداوم یک متغیر منطقه‌ای شده به تداوم رسانه زمین‌شناسی وابسته است و ممکن است تداوم را به معنای ریاضی ارائه ندهد. در این کار، ما از اصطلاح ویژگی برای یک متغیر منطقه‌ای شده، اصطلاح فیلد برای توزیع فضایی (شبه) پیوسته یک ویژگی و اصطلاح دامنه هدف استفاده خواهیم کرد. Ωبرای یک منطقه مورد علاقه وقتی ویژگی های جهانی و محلی را ذکر می کنیم، به ویژگی های آن اشاره می کنیم Ωو زیر مجموعه های آن Ωب، به ترتیب.

۲٫۲٫ درونیابی زمین آماری

هدف تکنیک های درونیابی زمین آماری تخمین یک مقدار در مکان های نمونه برداری نشده از یک ملک است Ωو پایه ای برای شبیه سازی های متوالی بسازید. محبوب ترین روش درونیابی زمین آماری کریجینگ است. در بخش‌های فرعی بعدی، به طور خلاصه نظریه کریجینگ را شرح می‌دهیم و بر انواع کریجینگ ساده آن (SK) تمرکز می‌کنیم. علاوه بر این، ما جنبه های محاسباتی عملی مانند همسایگی ها را مورد بحث قرار خواهیم داد.

۲٫۲٫۱٫ محله فضایی

از آنجایی که سیستم معادلات خطی برای تخمین های زمین آماری ممکن است بسیار بزرگ شود، این الگوریتم ها برای عملکرد معقول به نمونه گیری زیر مجموعه ای نیاز دارند. بنابراین، یک بیضی جستجوی سه بعدی می تواند برای یافتن همسایگان یک نقطه در یک مش استفاده شود [ ۲۴ ]. این بیضی را می توان با شش ویژگی تعریف کرد: آزیموت α; شیب β; غوطه γهمراه با شعاع در X rایکس، ی ryو جهت Z rzاز بیضی α، β، و γچرخش عقربه‌های ساعت بیضی حول محورهای Z، X و Y را دقیقاً به این ترتیب تعریف کنید. بر این اساس، ماتریس چرخش T را می توان به صورت تعریف کرد

تی=cosαگناهα۰-گناهαcosα۰۰۰۱۱۰۰۰cosβsinβ۰−sinβcosβcosγ۰−sinγ۰۱۰sinγ۰cosγ.

پس از ترجمه مش به گونه ای که xx=xy=xz=0 و چرخاندن آن بر اساس رابطه ( ۳ )، از رابطه ( ۴ ) می توان برای تعیین اینکه آیا یک نقطه ایکس”با مختصات تبدیل شده ایکسایکس”، ایکسy”و ایکسz”در داخل یا روی مرز بیضی جستجو قرار دارد (≤۱) یا نه (>1).

rایکسایکسایکس”۲+ryایکسy”2+rzایکسz”2≤۱

۲٫۲٫۲٫ واریوگرافی

تجزیه و تحلیل واریوگرافی یک پیش نیاز حیاتی برای بسیاری از تکنیک های درونیابی زمین آماری است. بدینوسیله، نیم متغیر تجربی نشان دهنده عدم تشابه تجمعی یک مجموعه گسسته از جفت نقطه با nجنشان دهنده تعداد جفت های نقطه در کلاس های فاصله است ساعتافزایش فاصله یکسان (معادله ( ۵ )).

γ(ساعت)=۱۲nج(ساعت)∑ک=۱nج(ساعت)z(ایکسک+ساعت)-z(ایکسک)۲

همتای پیوسته، که با نیمه متغیریگرام نظری نشان داده می شود γتیساعتهo، تقریبی از نیم متغیر تجربی است با فرض z(ایکس)یک میدان تصادفی ثابت [ ۲۵ ] باشد. γتیساعتهoبرای برازش واریوگرام تجربی استفاده می شود. مدل واریوگرام کروی γسپساعتبا اثر ناگت یک مدل تودرتوی محبوب است که برای برازش نیم‌واریوگرام تجربی [ ۲۶ و ۲۷ ] استفاده می‌شود که توسط محاسبه می‌شود

γ(ساعت)سپساعت=n+ب·۳|ساعت|۲آ-|ساعت|۳۲آ۳اگر۰≤|ساعت|<آnاگر|ساعت|≥آ،

با n قطعه، b آستانه و a محدوده [ ۶ ]. مدل واریوگرام یک تابع کوواریانس c را با رابطه نشان می دهد γ(ساعت)تیساعتهo=ج(۰)-ج(ساعت)، که در آن c یک تابع قطعی مثبت، زوج و ج(۰)=n+بدر مورد مدل واریوگرام کروی با اثر ناگت. نیمه متغیروگرام ها می توانند برای تعیین کمیت همبستگی مکانی یا زمانی یک متغیر تصادفی استفاده شوند [ ۲۷ ، ۲۸ ، ۲۹ ]. ج و γتیساعتهoمتغیرهای ورودی برای الگوریتم های درونیابی زمین آماری هستند.

۲٫۲٫۳٫ کریجینگ ساده

کریجینگ یک تکنیک تصادفی رایج برای درونیابی خواص سنگ های زمین شناسی در فضا و زمان است [ ۳۰ ]. برآوردگر کریجینگ بهترین برآوردگر خطی بی طرفانه (BLUE) یک ویژگی است زیرا واریانس خطا را به حداقل می رساند. این ساختار کوواریانس مقادیر نمونه برداری شده در سطح جهانی را در وزن ها برای پیش بینی ارزش ترکیب می کند. z(ایکس۰)در یک مکان نمونه برداری نشده ایکس۰[ ۳۱ ]. از این رو، z(ایکس۰)با وزن دادن به مقادیر مکان های نمونه گیری شده و ساخت ترکیبی خطی از آنچه می دهد محاسبه می شود

z(ایکس۰)=∑ک=۱nwک·z(ایکسک)،

جایی که wکوزن نقطه نمونه برداری شده است ایکسکبا ارزش z(ایکسک). انواع کریجینگ در درجه اول با اشتقاق آنها از بردار وزن متفاوت است. برای همه سیستم‌های کریجینگ، یک سیستم معادلات خطی باید حل شود همانطور که در پاراگراف‌های زیر توضیح داده شده است، که در آن ما تکنیک کریجینگ ساده (SK) [ ۳۲ ] را در نظر می‌گیریم و آن را با ادغام یک میانگین محلی متغیر [ ۳۳ ] گسترش می‌دهیم. ]. بنابراین، معادله ( ۷ ) را به آن تغییر می دهیم

z(ایکس۰)اسک=∑ک=۱nwک·z(ایکسک)+۱-∑ک=۱nwک·μ.

که در آن میانگین ساکن شناخته شده است μاضافه شده است [ ۶ ]. در حالی که SK این را فرض می کند μدر سطح جهانی ثابت و شناخته شده است، SK با میانگین متغیر محلی فرض می کند μثابت بودن فقط در همسایگی ایکس۰. برای به دست آوردن وزن های SK، سیستمی از n معادله خطی باید حل شود که در آن n نشان دهنده تعداد همسایگان در نظر گرفته شده است. این سیستم معادلات به این صورت تعریف می شود

آw=ب،

که مطابقت دارد

ج(ایکس۱-ایکس۱)⋯ج(ایکس۱-ایکسn)⋮⋱⋮ج(ایکسn-ایکس۱)⋯ج(ایکسn-ایکسn)⏟آw1اسک⋮wnاسک⏟w=ج(ایکس۱-ایکس۰)⋮ج(ایکسn-ایکس۰)،⏟ب

با c به عنوان تابع کوواریانس و ایکسnبه عنوان نقطه با مقدار معلوم [ ۲۵ ]. در SK هر نقطه درون یابی شده یک واریانس کریجینگ ساده ارائه می دهد σاسک۲[ ۵ ] که می توانیم با استفاده از فرمول محاسبه کنیم

σاسک۲=ج(۰)-∑ک=۱nwکج(ایکسک،ایکس۰).

کیفیت درونیابی کریجینگ به مدل واریوگرام و تناسب آن با نیم متغیر تجربی بستگی دارد.
۲٫۲٫۴٫ در نظر گرفتن واریانس خطای اندازه گیری

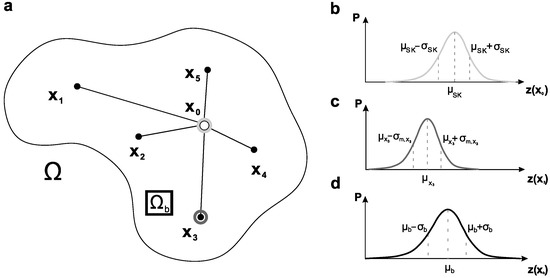
قبلاً دیدیم که کریجینگ به خودی خود یک خطای درون یابی محلی ایجاد می کند، یعنی: σاسک۲. با این حال، مؤلفه های دیگری نیز وجود دارد که نتیجه درون یابی را مغایر می کند. بعلاوه σاسک۲، تنوع محلی و ناشناخته از z(ایکس)که در Ωبو همچنین واریانس خطای اندازه گیری σمتر۲ممکن است نقش مهمی ایفا کند ( شکل ۲ ). یکپارچه سازی σمتر۲با تخمین دقت خطای اندازه گیری می توان به درون یابی دست یافت σمتربا واریانس از σمتر۲و ادغام آن در سیستم کریجینگ معادلات خطی

ج(ایکس۱-ایکس۱)+σ۱۲⋯ج(ایکس۱-ایکسn)⋮⋱⋮ج(ایکسn-ایکس۱)⋯ج(ایکسn-ایکسn)+σn2w1اسک⋮wnاسک=ج(ایکس۱-ایکس۰)⋮ج(ایکسn-ایکس۰).

برخلاف فرمول معمولی، σمتر۲با توجه به مقدار شناخته شده در نظر گرفته شده در ایکسکدر قطر ماتریس [ ۲۵ ] اضافه می شود. این به دلیل ماهیت ناهمگون پارامترهای زمین شناسی است زیرا معمولاً برای مقادیر بالا تغییرپذیری بالاتر و برای مقادیر کم تغییرپذیری کمتری نشان می دهند.

۲٫۳٫ شبیه سازی ترتیبی

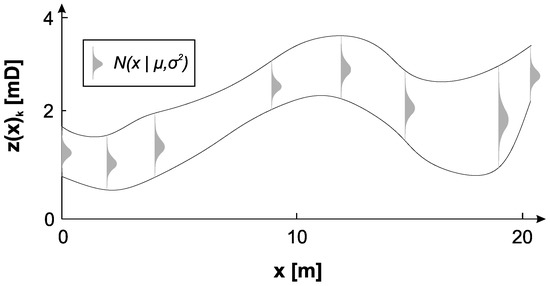
برخلاف تکنیک های درونیابی زمین آماری، شبیه سازی های متوالی با هدف بازتولید آمار جهانی در قالب مدل واریوگرام در نظر گرفته شده و هیستوگرام جهانی انجام می شود. بنابراین، به منظور محاسبه ناهمگنی فضایی یک ویژگی سنگ، می‌توان از شبیه‌سازی گاوسی متوالی (SGS) و الگوریتم شبیه‌سازی متوالی مستقیم (DSS) برای شبیه‌سازی تک متغیره استفاده کرد. SGS بر اساس رویکرد چند گاوسی [ ۳۳ ] است، که فرض می‌کند خطای کریجینگ استاندارد است که معمولاً با توزیع معمولی μ= ۰ و σاسک۲= ۱٫ این مستلزم آن است که هر تابع چگالی تجمعی یک نقطه‌ای (CDF) از هر ترکیب خطی RV به طور معمول توزیع شود، همه زیر مجموعه‌های RF نرمال چند متغیره باشند، توزیع دو نقطه‌ای نرمال باشد و همه توزیع‌های شرطی زیر مجموعه های RF طبیعی هستند [ ۳۳ ]. اگر RF الزامات را برآورده کند، تخمین کریجینگ ساده و واریانس CDF تجمعی خلفی را با در نظر گرفتن مدل واریوگرام نمره نرمال مشخص می‌کند. بنابراین، ما باید CDF توزیع اصلی را به فضای عادی استاندارد برای SGS تبدیل کنیم. به منظور تبدیل هر نقطه در CDF ( اف(ز(تو))) از هر متغیر تصادفی ز(تو)به یک تابع تصادفی Y(تو)و بالعکس می توان معادله زیر را اعمال کرد

Y(تو)=ϕ(ز(تو))=جی-۱[اف(ز(تو))]،

جایی که جی-۱CDF گاوسی معکوس است Y(تو)، که تابع چندک نیز نامیده می شود [ ۳۴ ] و  ϕ CDF گاوسی معکوس است اف(ز(تو)). بنابراین، z و y با احتمالات مشابهی مطابقت دارند. برای هر نقطه از قبل درون یابی شده است ایکسjاکنون یک مقدار تصادفی از توزیع نرمال است نμاسک،σاسک۲، که PDF آن را به صورت تعریف می کند

f(ایکس)=۱σ۲πه-۱۲ایکس-μσ۲،

به عنوان رسم شده است z(ایکس۰)با استفاده از تبدیل Box-Muller [ ۳۵ ]. ما می توانیم این تبدیل را با اعمال معادله انجام دهیم

z(ایکس۰)=-۲·ورود به سیستم(تو۱)·cos(2π·تو۲)·σ+μ،

با تو۱و تو۲به عنوان اعداد تصادفی ∈[۰،۱]، σبه عنوان انحراف معیار، و μبه عنوان میانگین توزیع اصلی. این شبیه‌سازی در نهایت با استفاده از یک تکنیک نقشه‌برداری برگشتی تبدیل چندک به فضای اصلی تبدیل می‌شود. بازتولید مدل کوواریانس، با این حال، تا زمانی که برآورد و واریانس از تخمین SK مشتق شده باشد، به رویکرد چند گاوسی نیاز ندارد [ ۹ ، ۱۰ ]. بنابراین، نوع توزیع شرطی، که به منظور شبیه‌سازی تغییرپذیری در هر نقطه انتخاب می‌شود، لزوماً نیازی به گاوسی بودن ندارد. با در نظر گرفتن این موضوع، بدیهی است که قبل از انجام یک شبیه سازی متوالی، نیازی به تبدیل نمره عادی نیست. این منجر به رویکرد DSS می‌شود که معمولاً از PDF جهانی با تعیین فاصله نمونه‌گیری از PDF محلی نمونه‌برداری می‌کند [ ۹ ]].

۲٫۴٫ اعتبار سنجی مدل

۲٫۴٫۱٫ اعتبار سنجی متقابل

به منظور ارزیابی کیفیت تحقق، مدل‌هایی که با استفاده از تکنیک‌های درون‌یابی یا شبیه‌سازی ساخته می‌شوند، باید اعتبارسنجی شوند. معمولاً درونیابی ها با اعتبارسنجی متقاطع تأیید می شوند. این تکنیک معمولاً با استفاده از روش‌های حذف نقطه به نام اعتبارسنجی متقاطع ترک p-out (LpO CV) انجام می‌شود. برای LpO CV، p نمونه‌های انتخاب شده به‌طور تصادفی از مجموعه داده‌های ورودی با اندازه n حذف می‌شوند. ۰<پ<nو درون یابی یا شبیه سازی بدون این نمونه ها انجام می شود [ ۳۶ ]. به عنوان معیارهای خوبی برازش، میانگین مربعات خطا (MSE، معادله ( ۱۶ ))، ریشه میانگین مربع خطا (RMSE، معادله ( ۱۷ ))، و میانگین خطای مطلق (MAE، معادله ( ۱۸ ) ) تحقق را می توان به صورت محاسبه کرد

ماسE=1n∑ک=۱nz^(ایکسک)-z(ایکسک)۲،

آرماسE=1n∑ک=۱nz^(ایکسک)-z(ایکسک)۲

و

مالفE=1n∑ک=۱n|z^(ایکسک)-z(ایکسک)|،

جایی که z^(ایکسک)نقاط شبیه سازی شده هستند. در حالی که ویلموت و همکاران. [ ۳۷ ] وضعیت نابرابری مثلث را برای RMSE که برای متریک تابع فاصله مورد نیاز است، سؤال می کنند، چای و دراکسلر [ ۳۸ ] نشان می دهند که RMSE در واقع این شرط را برآورده می کند. بنابراین، اگر خطاهای مدل از توزیع نرمال پیروی کنند، RMSE نسبت به MAE برتری دارد [ ۳۸ ].

۲٫۴٫۲٫ نوسانات ارگودیک
حداقل نیاز برای شبیه‌سازی‌های زمین‌آماری، توانایی آن‌ها در بازتولید داده‌های اصلی، آمار خلاصه جهانی و مدل واریوگرام جهانی است [ ۸ ، ۳۹ ]. نوسانات اردوژیک به اختلاف بین پارامترهای مدل و آمار تحقق ها اشاره دارد [ ۶ ]]. در مورد مدل واریوگرام، مغایرت یک تحقق با مدل واریوگرام به محدودیت محدودیت‌های یکپارچه به یک همسایگی محدود مربوط می‌شود. این در واقع منجر به خطاهای بالاتر در محدوده های دور در شبیه سازی می شود. در این مطالعه، ما نوسان ارگودیک یک تحقق را با تخمین میانگین MSE بین نیم‌واریوگرام تجربی و مدل واریوگرام اندازه‌گیری کردیم. اگر اختلاف یک تحقق بین مدل واریوگرام تجربی و واریوگرام از اختلاف مقادیر اصلی تجاوز نکند، گفته می‌شود که تولید مثل واریوگرام در محدوده نوسانات ارگودیکی قرار دارد.

۳٫ شبیه سازی ترتیبی با استفاده از مدل واریانس محلی

در این بخش توضیح خواهیم داد که چگونه الگوریتم های SGS و DSS برای نمونه برداری از مدل واریانس محلی (LVM) باید اصلاح شوند. LVM را می توان به عنوان یک نمایش جهانی از واریانس قابل مشاهده محلی توصیف کرد σLVم۲در یک سلول مش. بنابراین، LVM را می توان به عنوان ناهمگنی زمین شناسی محلی نام برد. LVM با استفاده از یک تکنیک نگاشت ساخته می شود که در آن مقدار واریانس های نگاشت شده توسط مجموعه ای از اندازه گیری ها محدود می شود. اینها برای نشان دادن تنوع در مقیاس کوچک موجود در موقعیت نقشه‌برداری شده در نظر گرفته شده‌اند. پس از آن، واریانس بر روی درون یابی می شود Ω. مفهوم اساسی درونیابی یک توزیع در فضا در شکل ۳ ج نشان داده شده است.

شبیه سازی های متوالی بر روی گره های انجام می شود Ωبا استفاده از اصلاح الگوریتم های SGS و DSS، یعنی LVM-SGS و LVM-DSS. ایده اصلی ما این است که اگر و فقط اگر ناهمگونی زمین شناسی بیش از حد باشد σاسک۲در ایکسک، ما از PDF ساخته شده توسط LVM به جای PDF مشتق شده از کریجینگ نمونه برداری می کنیم. در غیر این صورت، اگر خطای درون یابی بیشتر از ناهمگنی زمین شناسی قابل انتظار باشد، از PDF مشتق شده از کریجینگ نمونه برداری می کنیم. الگوریتم تعمیم یافته در الگوریتم ۱ نمایش داده شده است. همه تحلیل ها با نرم افزار منبع باز GeoReVi [ ۴۱ ] انجام شده است که در آن الگوریتم های جدید به عنوان پسوند در زبان برنامه نویسی C# ( پیوست A ) پیاده سازی شده اند.

الگوریتم ۱ LVM-SGS و LVM-DSS
  • داده شده: Ω; ایکس; N           ▷ دامنه هدف. مکان های نمونه برداری شده؛ اطلاعات محله؛
  • مقدار دهی اولیه: توسیم; ایکس”                    ▷ مکان های شبیه سازی شده. همسایگان فضایی؛
  • اگر GMV-SGS پس
  •      Y(ایکس)←معادله ( ۱۳ ) ▷ تبدیل به فضای معمولی استاندارد
  • پایان اگر
  • γ(ساعت)←معادله ( ۵ ) ▷ واریوگرام تجربی را تخمین بزنید
  • γ(ساعت)سپساعت←معادله ( ۶ ) ▷ مدل واریوگرام و تابع کوواریانس را استخراج کنید
  • برای همه تومنکه در Ω انجام دادن
  •      ایکس”←معادله ( ۳ ) و معادله ( ۴ ) ▷ همسایگی با N اعمال شده را تعیین کنیدایکس& توسیم
  •      μاسک←معادله ( ۸ ) با استفاده از γ(ساعت)سپساعت                         ▷ از ایکس”
  •      σاسک۲←معادله ( ۱۱ ) با استفاده از γ(ساعت)سپساعت                       ▷ از ایکس”
  •     اختصاص دهید σLVم(ایکسمن”)۲
  •     اگر σاسک۲≥σLVم(ایکسمن”)۲ سپس
  •          z(تومن)←معادله ( ۱۵ ) از نμاسک،σاسک۲            ▷ یک مقدار با σاسک۲
  •     دیگر
  •          z(تومن)←معادله ( ۱۵ ) از نμاسک،σLVم۲          ▷ یک مقدار با σLVم۲
  •     پایان اگر
  •     اضافه کردن z(تومن)به توسیم
  • پایان برای
  • اف(ز(تو))←معادله ( ۱۳ )، ▷ مقادیر شبیه سازی شده را به فضای اصلی تبدیل کنید

۳٫۱٫ مطالعه موردی

به منظور آزمایش و ارزیابی گردش کار جدید با الگوریتم‌های اصلاح‌شده، ما یک مطالعه آنالوگ رخنمون را در معدنی در آلمان انجام دادیم. در بخش‌های فرعی بعدی، هدف بررسی، استراتژی نمونه‌گیری و تکنیک‌های مدل‌سازی مورد استفاده برای پیاده‌سازی الگوریتم‌های LVM-SGS و LVM-DSS را تشریح خواهیم کرد. ما تصمیم گرفتیم از K نفوذپذیری ذاتی برای اجرا استفاده کنیم زیرا این ویژگی نقش مهمی در انواع مختلفی از استفاده از زیرسطحی ایفا می کند – به ویژه با توجه به مخازن زیرسطحی.

۳٫۱٫۱٫ موضوع تحقیق

یک رخنمون ماسه سنگ به طور فعال استخراج شده (طولانی ۷٫۶۴۷۵۴۶، lat. 49.523821) در Obersulzbach، که در حوضه Saar-Nahe در جنوب غربی آلمان واقع شده است، به عنوان موضوع بررسی انتخاب شده است ( شکل ۳ a). این رخنمون سازند دیزیبودنبرگ از گروه روتلیجند درون‌واریسکن را نشان می‌دهد، که یک واحد مخزن هیدروترمال بالقوه عمیق [ ۴۲ ] در گرابن راین بالایی شمالی را تشکیل می‌دهد. سازند دیزیبودنبرگ در معدن از دو دنباله بوما تشکیل شده است ( شکل ۳ب) از دلتای دریاچه ای که در زمان پرمین رسوب کرده است. دو معیار انتخاب تعیین کننده برای انتخاب معدن وجود داشت. از یک طرف، بسترهای رسوبی ≥۲ متر ضخامت دارند و به صورت جانبی پیوسته هستند. علاوه بر این، رخنمون به طور فعال استخراج می شود، که تاثیر هوازدگی اخیر را بر نفوذپذیری کاهش می دهد. علاوه بر این، امکان استخراج هر دو نمونه سنگ از دیواره رخنمون و همچنین مکعب‌های سنگ جهت‌یافته از انواع مختلف رخساره‌های سنگی به منظور انجام تحقیقات سه‌بعدی چند مقیاسی وجود داشت. رخنمون اندازه گیری می کند ۵۰×۱۵×۱۰m و بنابراین دارای اندازه یک سلول معمولی در مدل‌های مخزن استاتیکی و دینامیکی رایج است (به عنوان مثال، در [ ۴۴ ] را ببینید).
۳٫۱٫۲٫ استراتژی نمونه گیری
مطالعات متعدد نشان داد که تنوع فیزیکی در محیط های زمین شناسی باید به عنوان تابعی از حجم اندازه گیری، که به عنوان حجم ابتدایی نماینده (REV) نیز شناخته می شود، یکپارچه شود [ ۴۵ ]. REV حجمی را نشان می دهد که در آن مقدار معرف ناهمگنی با یک اندازه گیری [ ۴۶ ] به حداقل رساندن نوسانات در مقیاس کوچکتر گرفته می شود. بنابراین، یک رویکرد چند مقیاسی بر اساس مفهوم REV اجرا شده است. بر این اساس، ۳۹ نمونه سنگ استوانه‌ای به قطر و طول چهار سانتی‌متر از دیواره رخنمون استخراج شد. نمونه ها از شش پروفیل ۱ بعدی که کل منطقه معدن را پوشش می دهند ( شکل ۴ الف) گرفته شد. اطلاعات بیشتر در مورد موقعیت ها و جهت گیری های نمونه را می توان در Linsel [41 ]. این نمونه ها برای شبیه سازی میدان جهانی استفاده شد.
معدن شامل توالی هایی از یک میله دهانی پرودلتا است که به صورت چگال های turbiditic نهشته شده است. توالی ها از یک محیط رسوبی پرانرژی در پایه به یک محیط کم انرژی در بالا تغییر می کنند زیرا سرعت جریان به طور پیوسته در حال کاهش است. توالی‌ها از ماسه‌سنگ‌های ناهمگن و غنی از داخل کلاس در پایه و از ماسه‌سنگ‌های متقاطع بستر، موج‌دار و ماسه‌سنگ‌های همگن در بالا تشکیل شده‌اند. در نتیجه، توالی‌ها را می‌توان به‌عنوان توالی‌های Bouma حاوی فواصل Bouma A تا Bouma E در یک محیط رسوبی دریاچه‌ای-دلتایی تحت سلطه رودخانه‌ها [ ۴۷ ] اعلام کرد. بر اساس آن، ما فرض کردیم که تنوع در یک دنباله بوما در پایه بالاترین و در بالا کمترین است ( شکل ۳ ب).
بر این اساس، دو مکعب سنگ از ۰٫۲×۰٫۲×۰٫۲m (OSB2_c) و ۰٫۲۵×۰٫۲۵×۰٫۲۵m (OSB1_c) گرفته شد – یکی از بالا (Bouma E) و یکی از پایه (Bouma A) یک دنباله – به منظور گرفتن بیشترین و کمترین تنوع. محل قرارگیری مکعب ها در معدن و لایه ها در شکل ۳ a,b نشان داده شده است.
ما دو نوع رخساره را انتخاب کردیم: OSB1_c، یک نوع رخساره‌های غیرپیوسته با بستر متقاطع، غنی از داخل کلاس و OSB2_c، یک نوع رخساره‌های همگن بدون سطوح مرزی داخلی قابل مشاهده ماکروسکوپی. در مجموع، ۷۹ استوانه سنگ از مکعب سنگ OSB1_c و ۲۹ استوانه از OSB2_c استخراج شد. اطلاعات بیشتر در مورد فرآیند نمونه گیری را می توان در Linsel et al. [ ۴۰ ]. از این نمونه ها برای محدود کردن LVM استفاده شد.
۳٫۱٫۳٫ اندازه گیری های آزمایشگاهی
نمونه‌های استوانه‌ای برش داده شدند و در دمای ۱۰۵ در فر خشک شدند ∘C و در آزمایشگاه برای تعیین نفوذپذیری گاز ذاتی k در شرایط غیر اشباع اندازه گیری شد. k را می توان یکی از پارامترهای کلیدی سنگ های مخزن زمین گرمایی با توجه به سیستم های گرمابی در سفره های متخلخل [ ۴۸ ] در نظر گرفت. k با نفوذ سنج دارمشتات سلول هاسلر اندازه گیری شد. عملکرد دستگاه به تفصیل در Filomena و همکاران توضیح داده شده است. [ ۴۹ ]. نفوذپذیری در واحد میلیدارسی استاندارد صنعتی (mD) ارائه می شود، که در آن ۱ mD مربوط به ۹٫۸۶۹ × ۱۰ است. -۱۶متر ۲. اندازه گیری نفوذپذیری واریانس خطا بین ۰ و ۰٫۱۵ mD را ارائه می دهد ۲در محدوده مقادیر مشاهده شده [ ۵۰ ].
۳٫۱٫۴٫ نسل مش

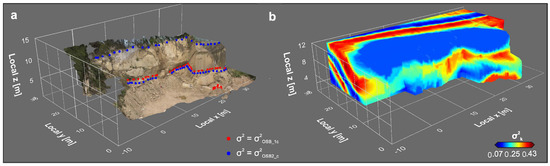
به منظور ساخت Ω، دیوار رخنمون با استفاده از یک نمایش فتوگرامتری مدل سازی شده است که نمونه برداری شده است ۴۰×۲۰چهره ها و متعاقباً با استفاده از درون یابی شپرد p -value IDW درون یابی شد، که می توانیم آن را به صورت بنویسیم

z(ایکس۰)=∑ک=۱n1/دکپ·z(ایکسک)∑ک=۱n1/دکپ،

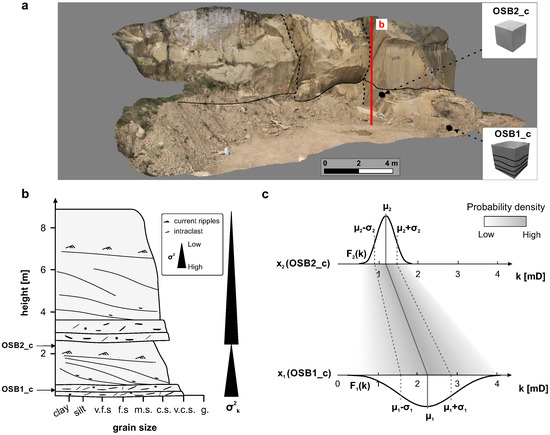
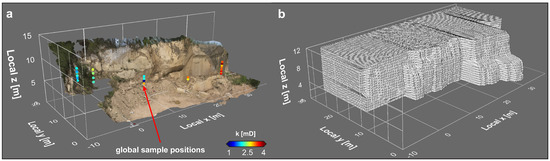
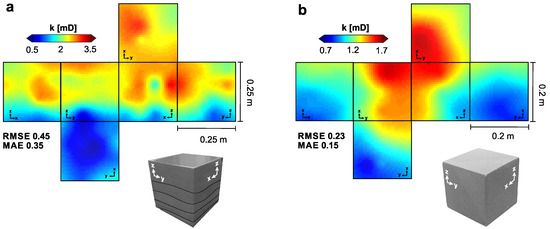
جایی که d فاصله اقلیدسی بین نقطه ای با مقدار شناخته شده است ایکسکو نقطه با مقدار مجهول ایکس۰و p یک عامل توان برای تأثیر غیرخطی وزن ها است. IDW با شعاع جستجوی کوتاه پنج متر و پارامتر قدرت چهار اعمال شده است. نتیجه درونیابی دارای RMSE 0.024 متر است که می تواند برای درونیابی سطحی کم در نظر گرفته شود. سطح رخنمون حاصل به عنوان یک سطح مرزی برای یک مش شش وجهی استفاده می شود که نشان دهنده Ω، که از ۷۵۲۴۰ سلول تشکیل شده است ( شکل ۴ ب، جدول ۱ ). مکعب های سنگ، که نشان دهنده Ωب، توسط یک شبکه متعامد و شش ضلعی که به ترتیب حاوی ۲۵۲۳۰ (OSB2_c) و ۶۴۰۰۰ سلول (OSB1_c) است ساخته شده اند. حجم یک سلول متوسط ​​از مش رخنمون تقریباً هشت برابر حجم OSB1_c و ۱۵ برابر حجم OSB2_c است ( جدول ۱ ).

واریانس σج۲به‌دست‌آمده از اندازه‌گیری‌های انجام‌شده بر روی نمونه‌ها از مکعب‌های سنگ، فرض می‌شود که واریانس را نشان می‌دهد σΩب۲که می توان در یک سلول از مش رخنمون انتظار داشت به طوری که

σLVم۲≈σΩب۲،

با σLVم۲واریانس نمونه محلی است که می توانیم با استفاده از فرمول آن را محاسبه کنیم

σ۲=۱n∑من=۱n(ایکسمن-μ)۲،

که در آن n تعداد کل نمونه ها است، μمیانگین و ایکسمننمونه در محل i است.

۴٫ نتایج

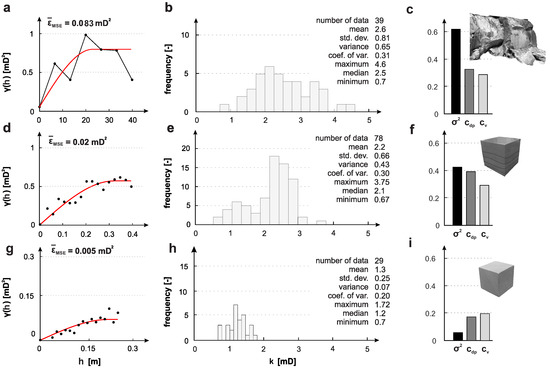
۴٫۱٫ تغییرپذیری فضایی

آنالیز واریوگرام محدوده ۰٫۳ متر و ۰٫۲ متر را برای نمونه های مکعب سنگ OSB1_c و OSB2_c به ترتیب و دامنه ۱۸ متر را برای نمونه های رخنمون نشان می دهد ( شکل ۵ a,d,g). آستانه در منطقه رخنمون کمی بالاتر است، همانطور که در مکعب های سنگ است. علاوه بر این، نمونه‌های رخنمون یک اثر قطعه ضعیف را نشان می‌دهند. به طور کلی، یک اثر مقیاس را می توان مشاهده کرد که در آن واریانس با حجم در نظر گرفته شده افزایش می یابد. این اثر در آمار توصیفی نیز وجود دارد ( شکل ۵ c,f,i).
اندازه گیری از ناحیه رخنمون نشان می دهد a جvاز ۰٫۲۸ و a جدپاز ۰٫۳۱٫ هیستوگرام توزیع نرمال k را در محدوده ۰٫۷ mD تا ۴٫۶ mD نشان می دهد ( شکل ۵ ب). یک آزمون دو طرفه کولموگروف-اسمیرنوف [ ۵۱ ]، که مبتنی بر اجرای سیمارد و اکویر [ ۵۲ ] است، این فرضیه را تایید کرد که همه نمونه ها از یک توزیع نرمال می آیند. استفاده از روش تشخیص پرت توکی [ ۵۳ ] هیچ گونه پرت آماری را در نمونه نشان نمی دهد. با استفاده از طرح طبقه بندی کوربت و جنسن [ ۵۴ ]، نمونه را می توان به عنوان بسیار همگن طبقه بندی کرد.
هیستوگرام محلی k از OSB1_c یک دووجهی را در اختلال در محدوده ۰٫۷ تا ۳٫۹ mD نشان می دهد ( شکل ۵ e). هیستوگرام OSB2_c یک محدوده تک وجهی از ۰٫۸ تا ۱٫۵ mD را نشان می دهد ( شکل ۵ h). باز هم، هیچ نقطه پرت آماری قابل تشخیص نیست. تنوع محلی OSB1_c به طور قابل توجهی بیشتر از OSB2_c است. k از OSB1_c یک را فراهم می کند جvاز ۰٫۳ و a جدپاز ۰٫۴ در حالی که اندازه گیری های OSB2_c مقادیر ۰٫۲ را برای نشان می دهد جvو ۰٫۱۸ برای جدپ. جvو جدپOSB1_c تمایل به پوشش تغییرپذیری داده های جهانی دارد. این نتیجه با نظریه REV از Nordahl و Ringrose [ ۴۵ ] مطابقت دارد. هر دو مکعب سنگ را می توان به عنوان بسیار همگن طبقه بندی کرد.
بنابراین، ما می توانیم یک تنوع قابل توجه در مقیاس کوچک را مشاهده کنیم. ساختارهای بستر در OSB1_c به خوبی در میدان نفوذپذیری درون یابی k حفظ می شوند ، که به تدریج از مقادیر کم بین ۰٫۷ و ۲ mD در بسترهای پایینی به مقادیر بالاتر بین ۲ و ۴ mD در بسترهای بالایی افزایش می یابد ( شکل ۶ a). در OSB2_c روند به صورت مورب از طریق مکعب سنگ در حال اجرا است ( شکل ۶ ب). با این حال، هیچ سطح مرزی ماکروسکوپی قابل مشاهده نیست، که می تواند کنترلی بر روی میدان k در اینجا داشته باشد. البته باید توجه داشت که محدوده k در اینجا به طور قابل توجهی در مقایسه با OSB1_c کوچکتر است.

۴٫۲٫ ساخت LVM

LVM با استفاده از نگاشت عناصر معماری سه بعدی از هر دو توالی بوما در معدن ساخته شده است. پایه و بالای دنباله ها نگاشت شده اند که برای محدود کردن LVM توسط واریانس قابل مشاهده محلی استفاده می شوند. σLVم۲. تجزیه و تحلیل داده های اکتشافی نشان می دهد که واریانس k در OSB1_c پنج برابر بزرگتر از OSB2_c است. این مطابق با نقشه برداری رسوبی است که نشان دهنده ناهمگنی بالاتر در پایه توالی بوما است.
فرض بر این است که OSB1_c ناهمگن ترین و OSB2_c همگن ترین نوع رخساره در توالی های بوما را نشان می دهد همانطور که در شکل ۳ ب نشان داده شده است. بر این اساس، موقعیت این نوع رخساره ها در سراسر منطقه معدن نقشه برداری شده و با σLVم۲که با اندازه گیری k OSB1_c و OSB2_c تعیین شده است. بنابراین، ما استفاده می کنیم σLVم۲=۰٫۴۳ برای نگاشت مرزهای پایه دنباله ها در سراسر ناحیه رخنمون. به همین ترتیب، σLVم۲=۰٫۰۷ به عنوان یک واریانس محلی برای بالاترین مرز توالی های منفرد استفاده می شود. مکان های نقشه برداری از σLVم۲در شکل ۷ الف نشان داده شده است. نقاط نگاشت شده بر روی مدل رخنمون متعاقباً درون یابی می شوند Ωبا استفاده از یک روش درونیابی مبتنی بر SK برای فایل های PDF پارامتریک ( شکل ۳ ج). درونیابی با استفاده از ۵ همسایه، برد پنج متر، آستانه ۰٫۰۰۵، قطعه ۰ و فرورفتن ۱۰ انجام می شود. ∘همانطور که طبقات به آرامی به سمت جنوب فرو می روند. شکل ۷ b LVM ساخته شده را نشان می دهد که توسط الگوریتم های شبیه سازی متوالی استفاده می شود. لازم به ذکر است که ما در LVM در ناحیه پهنه های گسل مرکزی، افست مناسبی داریم.

۴٫۳٫ بهینه سازی BLUE برای شبیه سازی متوالی

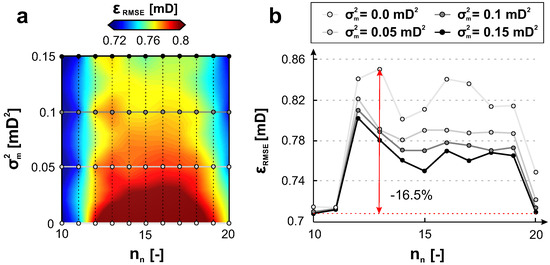
قبل از شبیه سازی متوالی، شرایط SK بهینه با توجه به واریانس خطای اندازه گیری یکپارچه σمتر۲و محله انتخابی مشخص می شود. بنابراین، یک بهینه‌سازی برنامه‌نویسی اعداد صحیح ساده با استفاده از واریانس‌های خطای اندازه‌گیری متفاوت انجام می‌شود. ۰٫۰mD ۲ ≤σمتر۲≤۰٫۱۵mD ۲) و تعداد متفاوتی از همسایگان ( ۱۰≤nn≤۲۰) به عنوان محدودیت های نابرابری. می توانیم مسئله بهینه سازی را به صورت بیان کنیم

دقیقهσمتر۲∈آر،nn∈نϵاسک(σمتر۲،nn)موضوعبه۰≤σm2≤۰٫۱۵۱۰≤nn≤۲۰,

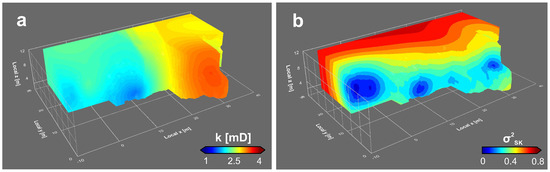
که در آن خطای SK ϵSKدر قالب RMSE و MAE باید به حداقل برسد. سطح پاسخ فرآیند بهینه سازی عددی نشان می دهد که خطای SK به طور کلی در حال کاهش است σm2در حال افزایش است. کمترین خطا با یک تولید می شود nnاز ۱۰، ۱۱ و ۲۰٫ این حساسیت خطای SK روی تعداد نقاط همسایه غیرعادی نیست. بهینه‌سازی عددی نشان می‌دهد که شرایط بهینه برای SK در آن برآورده می‌شود nn=20و σm2= 0.15 که RMSE 0.708 mD را به دست می دهد ( شکل ۸ ). خطای درون یابی را می توان ۱۶٫۵% برای RMSE و ۱۸٫۵% برای MAE کاهش داد. تحقق نهایی SK و توزیع فضایی σSK2برای آن مدل دقیق در شکل ۹ نشان داده شده است . لازم به ذکر است که توزیع فضایی از σSK2در یک شبیه سازی متوالی متفاوت است زیرا مکان های شبیه سازی شده قبلی نیز در نظر گرفته می شوند.

متغیرهای مدل سازی نهایی برای شبیه سازی های متوالی در جدول ۲ آورده شده است. برای SGS و LVM-SGS، داده های اصلی به فضای عادی استاندارد تبدیل می شوند μ= ۰ و σ= ۱٫ تبدیل منجر به انطباق مدل واریوگرام در نظر گرفته شده می شود زیرا آستانه اکنون ۱ است و نه ۰٫۷۵ با قطعه ۰ به جای ۰٫۰۵٫

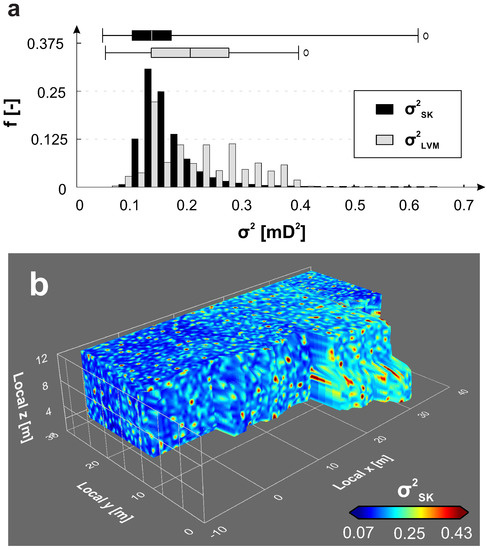
۴٫۴٫ σSK2در مقابل σLVM2

ویژگی های آماری و مکانی σSK2و σLVM2بسیار متفاوت است σSK2به صورت یکنواخت توزیع می شود، در حالی که σLVM2توزیع دووجهی را فراهم می کند ( شکل ۱۰ a). مشهود است که σSK2محدوده کل مدل کوواریانس در نظر گرفته شده را پوشش می دهد در حالی که σLVM2دامنه محدودتر است. احتمال شبیه سازی واریانس بین ۰٫۲ و ۰٫۴۳ mD ۲هنگام نمونه برداری از LVM به جای واریانس SK محلی، بالاتر است ( شکل ۱۰ ب). میانه بین σLVM2و σSK2≈ ۰٫۰۸ mD متفاوت است ۲، که نشان می دهد که تنوع شبیه سازی شده در تحقق الگوریتم های شبیه سازی متوالی مرسوم به طور سیستماتیک دست کم گرفته می شود.
با توجه به مدل واریوگرام، σLVM2دارای برد ۵ متر و آستانه ۰٫۳۶ mD ۲، و σSK2دارای برد ۰٫۳ متر و آستانه ۰٫۱ mD است ۲. بدین ترتیب، σSK2به نظر می رسد از نظر فضایی نامرتبط و تصادفی است. اما درجه تغییرپذیری در قسمت شرقی رخنمون کمی بیشتر از قسمت غربی است. بنابراین، در مقابل σLVM2، σSK2بدیهی است که الگوریتم شبیه سازی را با روند فضایی هنگام شبیه سازی تغییرپذیری محلی ارائه نمی دهد.

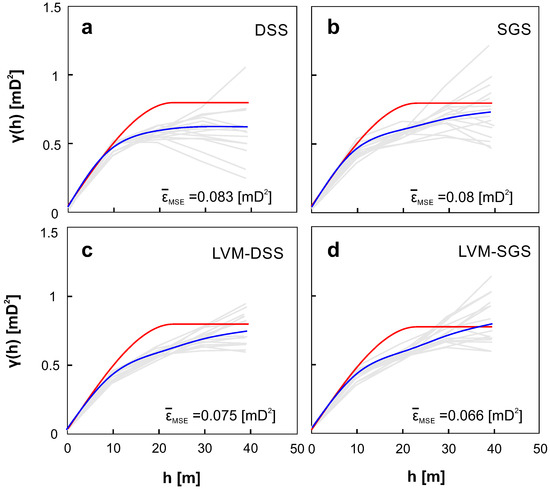
۴٫۵٫ اعتبار سنجی مدل

همه الگوریتم‌ها مدل واریوگرام در نظر گرفته شده را در محدوده نوسانات ارگودیک پس از تبدیل مجدد تولید می‌کنند ( شکل ۱۱ a-d). کیفیت بازتولید واریوگرام با محاسبه میانگین مربعات خطا ارزیابی شده است ϵ¯MSEاز تمام تحقق های بین واریوگرام تجربی و مدل واریوگرام. بهترین بازتولید توسط الگوریتم های LVM-DSS و LVM-SGS تولید می شود، در حالی که الگوریتم دومی کمترین درجه نوسانات ارگودیک را با ϵ¯MSE= 0.066 mD ۲. همه تحقق ها ناهمسانی های کوتاه برد را به خوبی بازتولید می کنند، اما کمی تفاوت را در محدوده های متوسط ​​دست کم می گیرند. DSS و SGS تمایل به دست کم گرفتن ملایم در محدوده های دور دارند که یک نقطه ضعف محله های محدود است. این اثر، با این حال، کمتر در الگوریتم های مبتنی بر LVM بیان شده است. برای هر دو نوع شبیه‌سازی متوالی، الگوریتم مبتنی بر LVM از رویکردهای شبیه‌سازی شرطی مرسوم بهتر عمل می‌کند.

خروجی های بصری

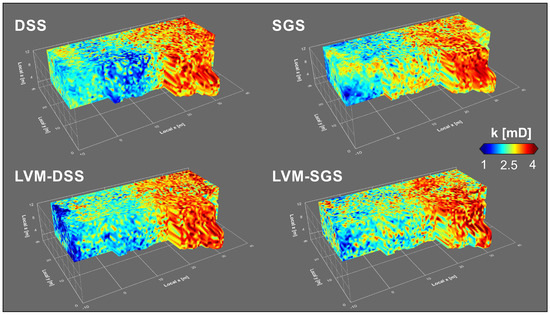
بدیهی است که همه الگوریتم های شبیه سازی نتایج قابل مقایسه بصری را ارائه می دهند ( شکل ۱۲ ). لازم به ذکر است که چهارضلعی های مدل های سه بعدی با استفاده از طرح Catmull-Clark [ ۵۵ ] برای تجسم تقسیم می شوند. در این طرح، یک نقطه جدید در یک چهارضلعی محاسبه می شود

ایکسjک+۱=۱n∑من=۰n-1ایکسمنک،

با ایکسjک+۱به عنوان نقطه جدید در مرحله تقسیم ک+۱در مرکز عنصر j با n راس در مرحله تقسیم k . این تکنیک الگوهای قابل مشاهده در مدل ها را صاف می کند. روندی آشکار در تمامی تحقق ها وجود دارد که نشان می دهد بیشترین مقادیر در قسمت شرقی معدن و کمترین مقادیر در قسمت غربی قرار دارد. با توجه به اینکه الگوریتم های اعمال شده مشروط هستند، این روند به خوبی با محدودیت های داده شده توسط اندازه گیری های جهانی مطابقت دارد، که همچنین بالاترین مقادیر را در قسمت شرقی معدن و کمترین مقدار را در قسمت غربی ارائه می دهد ( شکل ۴). آ). این روند به وضوح در تحقق DSS و LVM-DSS نشان داده شده است ( شکل ۱۲). SGS و DSS تمایل بیشتری به ایجاد مناطق همگن نسبت به معادل LVM خود دارند. بنابراین، آن الگوریتم‌ها ممکن است یک همگنی را نشان دهند که احتمالاً در لایه‌ها وجود ندارد. علاوه بر این، ناهمگونی معادل‌های LVM نسبت به مدل‌های تولید شده توسط الگوریتم‌های مرسوم به‌طور واقع‌بینانه‌تر در امتداد سطوح مرزی در معدن جهت‌گیری می‌کند.

۵٫ بحث

در این مطالعه، ما یک گردش کار ارائه می‌کنیم که تغییرات زمین‌شناسی قابل مشاهده محلی را در نسخه‌های اصلاح‌شده الگوریتم‌های شبیه‌سازی متوالی مرسوم به حساب می‌آورد. رویکردهای ما خروجی‌های مشابهی با الگوریتم‌های مرسوم تولید می‌کنند و مدل واریانس جهانی را همراه با آمار خلاصه جهانی که معیارهای مهمی برای اعتبار یک شبیه‌سازی آماری هستند، بازتولید می‌کنند [ ۸ ، ۱۰ ، ۳۹ ]. نتایج ما مفهوم REV [ ۴۵ ] را تأیید می کند، که در آن پیچیدگی یک متغیر تصادفی پیوسته با کاهش مقیاس مشاهده افزایش می یابد. علاوه بر این، ما می توانیم آن را تأیید کنیم σاسک۲هیچ معیاری برای دقت تخمین محلی [ ۵۶ ] ایجاد نمی کند زیرا فقط پیکربندی فضایی نقاط داده محدود کننده را منعکس می کند که به طور همزمان مستقل از مقادیر محدودیت ها هستند [ ۶ ]. با این حال، دو نکته وجود دارد که باید برای بحث در مورد مزایا و همچنین معایب رویکرد ما مطرح شود.

۵٫۱٫ ساخت LVM

منبع اصلی خطاها در گردش کار پیشنهادی بر اساس ساخت LVM است. LVM با یک رویکرد یکپارچه برای اندازه گیری تنوع محلی در همگن ترین و ناهمگن ترین انواع رخساره های سنگی در توالی رسوبی به دست آمده است. تجزیه و تحلیل آماری نشان داد که این فرض درست است زیرا معیارهای ناهمگونی در OSB1_c تنوع بالاتری را نشان می‌دهد که در OSB2_c وجود دارد. این در واقع پایه و اساس این مطالعه را می سازد. واریانس در پایه و بالای یک دنباله بوما ثابت فرض شده است. این فرض با تعداد نمونه های گرفته شده در این مطالعه موردی محدود می شود. با ساخت LVM با درون یابی SK، فرض می کنیم که واریانس در یک دنباله رسوبی بوما از نظر ریاضی پیوسته است. این فرض ممکن است در مطالعات آینده بسیار ساده باشد. به منظور اعتبارسنجی این نتایج، نمونه های محلی بیشتری برای محدود کردن LVM لازم است. این یک اشکال در مقایسه با الگوریتم‌های SGS و DSS معمولی است زیرا این الگوریتم‌ها به تخمین مدل تنوع جهانی وابسته نیستند.

۵٫۲٫ مقایسه توزیع فضایی واریانس محلی

شکل ۱۳ a,b رابطه بین LVM و تحقق DSS (a) و تحقق LVM-DSS را به ترتیب (b) نشان می دهد. اگرچه روند کلی در بین هر دو نوع شبیه‌سازی یکسان باقی می‌ماند، توزیع فضایی تنوع محلی نامرتبط و ذاتاً متفاوت است. در تحقق DSS، ناهمگونی در منطقه به طور تصادفی توزیع شده است. ناهمگن ترین نواحی در تحقق LVM-DSS در نواحی نوری قرار دارند که در آن ها σLVم۲بالا است – در حالی که همگن ترین مناطق در مناطق تاریک زندگی می کنند – جایی که σLVم۲کم است. به عنوان توزیع فضایی σاسک۲الگوریتم‌های SGS و DSS، بر خلاف اصلاحات مبتنی بر LVM، در درجه اول به فاصله تا همسایه‌های محدودکننده وابسته است، نمی‌توانند توزیع فضایی واقعی تنوع زمین‌شناختی محلی را توضیح دهند. این مشاهدات به صورت مفهومی در شکل ۱۳ ج نشان داده شده است که رابطه فضایی بین σاسک۲و σLVم۲، همانطور که نتایج مطالعه ما نشان می دهد. بدیهی است که الگوریتم های مرسوم تنوع زمین شناسی محلی را در محدوده های نزدیک به داده های شرطی دست کم می گیرند. همچنین مشهود است که σاسک۲به طور سیستماتیک تنوع طبیعی موجود در محیط زمین شناسی را دست کم می گیرد که در این مطالعه بررسی شده است ( شکل ۱۰ a). بنابراین، SGS و DSS ممکن است نتوانند کل تنوع زمین‌شناسی را همانطور که در این مطالعه نشان داده شده است، بازتولید کنند، که در عوض مزیت الگوریتم‌های پیشنهادی است.

۶٫ نتیجه گیری

در این مطالعه، ما یک گردش کار جدید را پیشنهاد می کنیم که تنوع مشاهده شده به صورت محلی را در بر می گیرد σLVم۲به شبیه سازی های متوالی ما می‌توانیم واریانس کریجینگ ساده محلی را نشان دهیم σاسک۲متفاوت است σLVم۲در حجم های محلی منطقه هدف. بنابراین، الگوریتم های DSS و SGS با جایگزینی اصلاح شده اند σاسک۲از طریق اندازه گیری مشتق شده است σLVم۲در یک سلول مش این جایگزینی اگر و فقط اگر انجام شده است σLVم۲≥σاسک۲. LVM با استفاده از نقشه‌برداری زمین‌شناسی و با این فرض ساخته شده است که تنوع در سنگ‌شناسی ناهمگن‌ترین و کمترین در کم‌ترین سنگ‌شناسی ناهمگن در یک دنباله بوما است. رویکرد پیشنهادی می‌تواند در هر نوع شبیه‌سازی ویژگی‌های فضایی استفاده شود، اما به‌ویژه برای رسانه‌های زمین‌شناسی طراحی شده است.
رویکردهای LVM-DSS و LVM-SGS تنوع مشاهده شده در جانشینی رسوبی را به اندازه کافی بازتولید می کنند و در عین حال حداقل معیارهای آماری مورد نیاز یک شبیه سازی معتبر شامل هیستوگرام جهانی، ناهمگنی جهانی و مدل واریوگرام را بازتولید می کنند. علاوه بر این، بر خلاف نمایندگان مرسوم خود، الگوریتم‌های مبتنی بر LVM توزیع فضایی واریانس محلی مورد انتظار را به اندازه کافی محاسبه می‌کنند. هنگامی که LVM مشتق شد، ممکن است در سایر الگوریتم های شبیه سازی زمین آماری مانند روش باندهای چرخشی [ ۵۷ ، ۵۸ ، ۵۹ ، ۶۰ ] ادغام شود.
از نتایج ما موارد زیر را نتیجه می گیریم.
  • معیارهای فاصله RMSE و MAE در درونیابی های فضایی را می توان با توجه به واریانس خطای اندازه گیری و همسایگی بهینه بهینه کرد.
  • نمونه‌های زمین‌شناسی همیشه زیرمجموعه کوچکی از تنوع محلی را نشان می‌دهند که حداقل باید با نمونه‌برداری با وضوح بالا و به صورت تصادفی در نظر گرفته شود.
  • واریانس کریجینگ ساده لزوماً برای بزرگی تنوع محلی در رسانه های زمین شناسی و قطعاً برای توزیع فضایی آن حساب نمی کند.
  • این واقعیت که واریانس کریجینگ ساده محلی یک روند زمین‌شناسی را منعکس نمی‌کند، ممکن است هنگام استفاده از مدل‌های مشتق‌شده از شبیه‌سازی متوالی به عنوان پایه‌ای برای فرآیندهای بهره‌برداری زیرسطحی، منجر به مشکلات پیش‌بینی نشده شود، زیرا ممکن است ناهمگونی کامل زمین‌شناسی به درستی در نظر گرفته نشده باشد.
  • با معرفی یک مدل واریانس محلی مبتنی بر زمین شناسی محدود شده با اندازه گیری، توزیع فضایی واریانس مورد انتظار در معدن مورد بررسی را می توان در شبیه سازی های متوالی ادغام کرد. این امکان شبیه سازی تنوع زمین شناسی را فراهم می کند، که ممکن است بیشتر از تغییرپذیری شبیه سازی شده در الگوریتم های شبیه سازی متوالی مرسوم باشد.
تحقیقات آتی باید بر مقایسه متمرکز شود σSK2و σLVM2تحت در نظر گرفتن سایر خواص فیزیکوشیمیایی، سایر تنظیمات زمین شناسی، و مقیاس های دیگر. این ممکن است مستلزم تطبیق مفروضات در مورد تداوم فضایی تنوع باشد که با این حال، همیشه باید بر اساس تجزیه و تحلیل های زمین شناسی قابل اعتماد باشد.

اختصارات

در این نسخه از اختصارات زیر استفاده شده است:

CDF تابع توزیع تجمعی
DSS شبیه سازی ترتیبی مستقیم
LVM مدل واریانس محلی
CV LpO اعتبار سنجی متقاطع را ترک کنید
MAE میانگین-مطلق-خطا
MSE خطای میانگین مربع
PDF تابع چگالی احتمال
REV نماینده حجم ابتدایی
RMSE خطای ریشه میانگین مربع
RF تابع تصادفی
RV متغیر تصادفی
SGS شبیه سازی گاوسی متوالی
SK کریجینگ ساده

پیوست A. کد و در دسترس بودن داده ها

GeoReVi یک نرم افزار منبع باز برای سیستم های ویندوز است که در https://github.com/ApirsAL/GeoReVi موجود است. داده ها در https://www.doi.org/10.6084/m9.figshare.11791407.v2 موجود است .

منابع

  1. لی، اچ. رینولدز، جی. در تعریف و کمیت ناهمگنی. Oikos ۱۹۹۵ ، ۷۳ ، ۲۸۰-۲۸۴٫ [ Google Scholar ] [ CrossRef ]
  2. کرویجمانس، RA; ویلمز، CJL; نیک، اچ ام. Bruhn، DF تأثیر ناهمگونی رخساره بر عملکرد دوگانه در مخازن رسوبی زمین گرمایی کم آنتالپی. Geothermics ۲۰۱۶ ، ۶۴ ، ۲۰۹-۲۱۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  3. رودریگو-ایلاری، جی. ریزینگر، ام. گومز-هرناندز، JJ تأثیر ناهمگونی بر شبیه‌سازی‌های انتقال حرارت در سیستم‌های زمین گرمایی کم عمق. در زمین آمار والنسیا ۲۰۱۶ ; Springer: برلین، آلمان، ۲۰۱۷; صص ۸۴۹-۸۶۲٫ [ Google Scholar ] [ CrossRef ]
  4. شپرد، دی. تابع درونیابی دو بعدی برای داده های با فاصله نامنظم. در مجموعه مقالات کنفرانس ملی ACM 1968، نیویورک، نیویورک، ایالات متحده آمریکا، ۲۷-۲۹ اوت ۱۹۶۸; صص ۵۱۷-۵۲۴٫ [ Google Scholar ] [ CrossRef ]
  5. وبستر، آر. مارگارت، AO Geostatistics for Environmental Scientists , ۲nd ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; پ. ۳۳۰٫ [ Google Scholar ]
  6. Deutsch، CV; Journel , A. GSLIB: کتابخانه نرم افزار زمین آماری و راهنمای کاربر . انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، ۱۹۹۸٫ [ Google Scholar ]
  7. Tran, TT بهبود تولید مثل واریوگرام در شبکه های شبیه سازی متراکم. محاسبه کنید. Geosci. ۱۹۹۴ ، ۲۰ ، ۱۱۶۱-۱۱۶۸٫ [ Google Scholar ] [ CrossRef ]
  8. Leuangthong، O. مک لنان، جی. Deutsch، CV حداقل معیارهای پذیرش برای تحقق زمین آماری. نات. منبع. Res. ۲۰۰۴ ، ۱۳ ، ۱۳۱-۱۴۱٫ [ Google Scholar ] [ CrossRef ]
  9. Soares، A. شبیه سازی متوالی مستقیم و شبیه سازی. ریاضی. جئول ۲۰۰۱ ، ۳۳ ، ۹۱۱-۹۲۶٫ [ Google Scholar ] [ CrossRef ]
  10. رابرتسون، RK; مولر، UA; بلوم، شبیه سازی متوالی مستقیم LM با بازتولید هیستوگرام: مقایسه الگوریتم ها محاسبه کنید. Geosci. ۲۰۰۶ ، ۳۲ ، ۳۸۲-۳۹۵٫ [ Google Scholar ] [ CrossRef ]
  11. ژورنل، ا. آلابرت، اف. گسترش داده های غیر گاوسی در علوم زمین. Terra Nova ۱۹۸۹ ، ۱ ، ۱۲۳-۱۳۴٫ [ Google Scholar ] [ CrossRef ]
  12. ورلی، جی. شبیه‌سازی گاوسی متوالی: روش مونت کارلو برای تولید مدل‌های تخلخل و نفوذپذیری. در تولید، انباشت و تولید هیدروکربن های اروپا III ; اسپنسر، AM، اد. Springer: برلین/هایدلبرگ، آلمان، ۱۹۹۳; صص ۳۴۵-۳۵۶٫ [ Google Scholar ]
  13. ارسوی، ا. Yünsel، TY شبیه سازی شرطی زمین آماری برای ارزیابی ویژگی های کیفی ذخایر زغال سنگ Cayırhan. کاوش انرژی بهره برداری. ۲۰۰۶ ، ۲۴ ، ۳۹۱-۴۱۶٫ [ Google Scholar ] [ CrossRef ]
  14. دلبری، م. افراسیاب، پ. Loiskandl، W. استفاده از شبیه‌سازی گاوسی متوالی برای ارزیابی عدم قطعیت فضایی در مقیاس میدانی محتوای آب خاک. CATENA ۲۰۰۹ ، ۷۹ ، ۱۶۳-۱۶۹٫ [ Google Scholar ] [ CrossRef ]
  15. پینیرو، ام. امری، ایکس. میراندا، تی. لاماس، ال. اسپادا، ام. مدل سازی ناهمگونی های ژئوتکنیکی با استفاده از شبیه سازی زمین آماری و تجزیه و تحلیل تفاوت های محدود. Minerals ۲۰۱۸ ، ۸ ، ۵۲٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  16. جعبه، GEP؛ مولر، ME نکته ای در مورد تولید انحرافات طبیعی تصادفی. ان ریاضی. آمار. ۱۹۵۸ ، ۲۹ ، ۶۱۰-۶۱۱٫ [ Google Scholar ] [ CrossRef ]
  17. Matheron, G. اصول زمین آمار. اقتصاد جئول ۱۹۶۳ ، ۵۸ ، ۱۲۴۶-۱۲۶۶٫ [ Google Scholar ] [ CrossRef ]
  18. Anyiam، OA; اندرو، پی جی. Okwara، IC ارزیابی ناهمگنی و ارزیابی پتروفیزیکی مخازن در “میدان اکبر”، دلتای نیجر، نیجریه. جی. پت. کاوش کنید. تولید تکنولوژی ۲۰۱۷ ، ۷ ، ۱۰۳۵-۱۰۵۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. میچی، EAH؛ Haines، TJ تنوع و ناهمگنی خواص پتروفیزیکی سنگ‌های گسل کربنات کششی، مالت. حیوان خانگی Geosci. ۲۰۱۶ ، ۲۲ ، ۱۳۶-۱۵۲٫ [ Google Scholar ] [ CrossRef ]
  20. موکرجی، تی. ماوکو، جی. ریو، P. مقیاس ناهمگونی های مخزن و تاثیر تفکیک لرزه ای بر یکپارچگی زمین آماری. ریاضی. جئول ۱۹۹۷ ، ۲۹ ، ۹۳۳-۹۵۰٫ [ Google Scholar ] [ CrossRef ]
  21. De Ros، LF; Scherer، کنترل‌های چینه‌شناسی CMS بر روی توزیع فرآیندهای دیاژنتیکی، کیفیت و ناهمگونی مخازن رودخانه‌ای-بادی از حوضه Recôncavo، برزیل. در پیوند دیاژنز به چینه شناسی توالی ; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; صص ۱۰۵-۱۳۲٫ [ Google Scholar ] [ CrossRef ]
  22. فرهنگ لغت انگلیسی آکسفورد. ناهمگونی ؛ انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، ۲۰۱۴٫ [ Google Scholar ]
  23. Fitch، PJR؛ لاول، MA; دیویس، اس جی. پریچارد، تی. هاروی، PK یک رویکرد یکپارچه و کمی به ناهمگنی پتروفیزیکی. مارس پت. جئول ۲۰۱۵ ، ۶۳ ، ۸۲-۹۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. رمی، ن. بوچر، ا. Wu, J. زمین آمار کاربردی با SGeMS: راهنمای کاربر . انتشارات دانشگاه کمبریج: کمبریج، انگلستان، ۲۰۰۹٫ [ Google Scholar ] [ CrossRef ]
  25. Wackernagel, H. Multivariate Geostatistics , ۳rd ed.; Springer: برلین/هایدلبرگ، آلمان، ۲۰۰۳; پ. ۳۸۸٫ [ Google Scholar ] [ CrossRef ]
  26. آرمسترانگ، ام. واریوگرام های تجربی. در زمین آمار خطی پایه ; Springer: برلین/هایدلبرگ، آلمان، ۱۹۹۸; ص ۴۷-۵۸٫ [ Google Scholar ] [ CrossRef ]
  27. رینگروس، پی. Bentley, M. Reservoir Model Design , ۱st ed.; Springer: Dordrecht، هلند، ۲۰۱۵; پ. ۲۴۹٫ [ Google Scholar ] [ CrossRef ]
  28. گو، ی. Rühaak، W. پارس سگ.؛ Sass, I. استفاده از داده های لرزه ای برای تخمین توزیع فضایی هدایت حرارتی سنگ در مقیاس مخزن. Geothermics ۲۰۱۷ ، ۶۶ ، ۶۱-۷۲٫ [ Google Scholar ] [ CrossRef ]
  29. Rühaak، W. گوادانینی، آ. گایگر، اس. پارس سگ.؛ گو، ی. آرتز، ا. هوموث، اس. Sass, I. ارتقاء رسانایی حرارتی سازندهای رسوبی برای اکتشاف زمین گرمایی. Geothermics ۲۰۱۵ ، ۵۸ ، ۴۹-۶۱٫ [ Google Scholar ] [ CrossRef ]
  30. Rühaak, W. درونیابی ۳-بعدی داده های دمای زیرسطحی با خطای اندازه گیری با استفاده از کریجینگ. محیط زیست علوم زمین ۲۰۱۵ ، ۷۳ ، ۱۸۹۳-۱۹۰۰٫ [ Google Scholar ] [ CrossRef ]
  31. بیلی، تی. Gatrell، A. تجزیه و تحلیل داده های فضایی تعاملی . Longman Group Limited: هارلو، انگلستان، ۱۹۹۵; پ. ۴۳۲٫ [ Google Scholar ]
  32. Journel, AG تخمین ناپارامتری توزیع های فضایی. J. Int. دانشیار ریاضی. جئول ۱۹۸۳ ، ۱۵ ، ۴۴۵-۴۶۸٫ [ Google Scholar ] [ CrossRef ]
  33. Goovaerts, P. Geostatistics for Natural Resources Evaluation ; انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، ۱۹۹۷٫ [ Google Scholar ]
  34. Remy, N. روش‌های الگوریتمی و نرم‌افزاری برای ادغام بهتر اطلاعات زمین‌شناسی در مدل‌های عددی . دانشگاه استندفورد: استنفورد، کالیفرنیا، ایالات متحده آمریکا، ۲۰۰۴٫ [ Google Scholar ]
  35. اوکتن، جی. Göncü، A. ایجاد توالی با اختلاف کم از توزیع نرمال: جعبه-مولر یا تبدیل معکوس؟ ریاضی. محاسبه کنید. مدل. ۲۰۱۱ ، ۵۳ ، ۱۲۶۸-۱۲۸۱٫ [ Google Scholar ] [ CrossRef ]
  36. سلیس، الف. اعتبارسنجی متقاطع بهینه در تخمین چگالی با اتلاف L2. ان آمار ۲۰۱۴ ، ۴۲ ، ۱۸۷۹-۱۹۱۰٫ [ Google Scholar ] [ CrossRef ]
  37. ویلموت، سی جی; ماتسورا، ک. Robeson، SM ابهامات ذاتی در آمار خطاهای مبتنی بر مجموع مربعات. اتمس. محیط زیست ۲۰۰۹ ، ۴۳ ، ۷۴۹-۷۵۲٫ [ Google Scholar ] [ CrossRef ]
  38. چای، تی. Draxler، RR ریشه میانگین مربعات خطا (RMSE) یا میانگین خطای مطلق (MAE)؟ – استدلال هایی علیه اجتناب از RMSE در ادبیات. Geosci. مدل Dev. ۲۰۱۴ ، ۷ ، ۱۲۴۷-۱۲۵۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. Emery, X. تست درستی الگوریتم ترتیبی برای شبیه سازی میدان های تصادفی گاوسی. استوک. محیط زیست Res. ارزیابی ریسک ۲۰۰۴ ، ۱۸ ، ۴۰۱-۴۱۳٫ [ Google Scholar ] [ CrossRef ]
  40. لینسل، ا. ویزلر، اس. هورنونگ، جی. Hinderer، M. تجزیه و تحلیل با وضوح بالا ویژگی های فیزیکوشیمیایی محیط های ماسه سنگی در مقیاس رخساره های سنگی. بحث زمین جامد ۲۰۲۰ ، ۲۰۲۰ ، ۱-۲۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. Linsel, A. ApirsAL/GeoReVi: GeoReVi v1.0.0 Pre-Release. در دسترس آنلاین: https://zenodo.org/record/3541136#.XvhBb3ERWUk (دسترسی در ۲۰ دسامبر ۲۰۱۹).
  42. بکر، ا. شوارتز، ام. Schäfer, A. Lithostratigraphische Korrelation des Rotliegend im östlichen Saar-Nahe-Becken. Jahresberichte Und Mitteilungen Des Oberrheinischen Geologischen Vereins ۲۰۱۲ ، ۹۴ ، ۱۰۵-۱۳۳٫ [ Google Scholar ] [ CrossRef ]
  43. آرتز، ا. پارس سگ.؛ گوتز، AE; Sass، I. مطالعه آنالوگ رخنمون سازندهای مخزن ماسه سنگ زمین گرمایی پرموکربونیفر (شمال راین بالا گرابن، آلمان): تاثیر محتوای معدنی، محیط رسوبی و دیاژنز بر خواص پتروفیزیکی. بین المللی J. Earth Sci. ۲۰۱۵ ، ۱۰۵ ، ۱۴۳۱-۱۴۵۲٫ [ Google Scholar ] [ CrossRef ]
  44. فرخوتدینوف، آ. جام، پ. د فوکه، سی. Cherkasov، S. مطالعه موردی مدل‌سازی یک مخزن هیدروترمال: کانسار خانکالا از آب‌های زمین گرمایی. Geothermics ۲۰۱۶ ، ۵۹ ، ۵۶-۶۶٫ [ Google Scholar ] [ CrossRef ]
  45. نوردال، ک. Ringrose، PS شناسایی حجم ابتدایی نماینده برای نفوذپذیری در کانسارهای هترولیتیک با استفاده از مدل‌های سنگ عددی. ریاضی. Geosci. ۲۰۰۸ ، ۴۰ ، ۷۵۳٫ [ Google Scholar ] [ CrossRef ]
  46. نوردال، ک. مسینا، سی. برلند، اچ. روستاد، AB; ریمستاد، ای. مارتینیوس، AW; هاول، ج.ا. تأثیر خوب، TR مدل‌سازی چند مقیاسی بر توزیع تخلخل و نفوذپذیری پیش‌بینی‌شده در نهشته‌های رودخانه‌ای عضو لوند بالایی (میدان اسنور، فلات قاره نروژ). در هندسه رسوب-بدن و ناهمگنی: مطالعات آنالوگ برای مدل‌سازی زیرسطحی ; انجمن زمین شناسی لندن: لندن، انگلستان، ۲۰۱۴; جلد ۳۸۷، ص. ۲۵٫ [ Google Scholar ] [ CrossRef ]
  47. میدلتون، رسوب GV از جریان های کدورت. آنو. سیاره زمین کشیش. علمی ۱۹۹۳ ، ۲۱ ، ۸۹-۱۱۴٫ [ Google Scholar ] [ CrossRef ]
  48. آگهمار، تی. وبر، جی. شولز، آر. تولید انرژی زمین گرمایی عمیق در آلمان. انرژی ها ۲۰۱۴ ، ۷ ، ۴۳۹۷-۴۴۱۶٫ [ Google Scholar ] [ CrossRef ]
  49. Filomena، CM; هورنونگ، جی. استولهوفن، اچ. ارزیابی دقت اندازه‌گیری‌های نفوذپذیری گاز محور: مطالعه مقایسه‌ای دستگاه‌های نفوذ سنج سلولی هاسلر و پروب. زمین جامد ۲۰۱۴ ، ۵ ، ۱-۱۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  50. Bär, K. Untersuchung der tieFengeothermischen Potenziale von Hessen ; Technische Universität Darmstadt: دارمشتات، آلمان، ۲۰۱۲; پ. ۲۹۷٫ [ Google Scholar ]
  51. Massey, FJ آزمون کولموگروف-اسمیرنوف برای خوبی تناسب. مربا. آمار دانشیار ۱۹۵۱ ، ۴۶ ، ۶۸-۷۸٫ [ Google Scholar ] [ CrossRef ]
  52. سیمرد، ر. Ecuyer, P. محاسبه توزیع دو طرفه Kolmogorov-Smirnov. J. Stat. نرم افزار ۲۰۱۱ ، ۱ . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  53. Tukey, J. تجزیه و تحلیل داده های اکتشافی ; Addison-Wesley: Reading، MA، ایالات متحده آمریکا، ۱۹۷۷; پ. ۷۱۲٫ [ Google Scholar ]
  54. کوربت، پی. Jensen, JL برآورد نفوذپذیری متوسط: به چند اندازه گیری نیاز دارید؟ First Break ۱۹۹۲ , ۱۰ , ۵٫ [ Google Scholar ] [ CrossRef ]
  55. Catmull, E. A Subdivision Algorithm for Computer Display of Curved Surfaces ; دانشگاه یوتا: سالت لیک سیتی، یوتا، ۱۹۷۴٫ [ Google Scholar ]
  56. Journel, AG Geostatistics: مدل ها و ابزارهایی برای علوم زمین. ریاضی. جئول ۱۹۸۶ ، ۱۸ ، ۱۱۹-۱۴۰٫ [ Google Scholar ] [ CrossRef ]
  57. Matheron، G. توابع تصادفی ذاتی و کاربردهای آنها. Adv. Appl. احتمالا. ۱۹۷۳ ، ۵ ، ۴۳۹-۴۶۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  58. منتوگلو، ع. Wilson, JL روش باندهای چرخشی برای شبیه‌سازی میدان‌های تصادفی با استفاده از تولید خط به روش طیفی. منبع آب Res. ۱۹۸۲ ، ۱۸ ، ۱۳۷۹-۱۳۹۴٫ [ Google Scholar ] [ CrossRef ]
  59. امری، ایکس. Lantuéjoul, C. TBSIM: یک برنامه کامپیوتری برای شبیه‌سازی شرطی میدان‌های تصادفی گاوسی سه‌بعدی از طریق روش باندهای چرخشی. محاسبه کنید. Geosci. ۲۰۰۶ ، ۳۲ ، ۱۶۱۵-۱۶۲۸٫ [ Google Scholar ] [ CrossRef ]
  60. پرواززار، س. امری، ایکس. مدنی، ن. مقایسه الگوریتم‌های گاوسی متوالی و باندهای چرخشی برای شبیه‌سازی درجه‌ها در نهشته‌های چند عنصری. Comptes Rendus Geosci. ۲۰۱۵ ، ۳۴۷ ، ۸۴-۹۳٫ [ Google Scholar ] [ CrossRef ]
در دسترس بودن نمونه: نمونه‌های سنگ مورد بررسی در موسسه علوم زمین کاربردی دارمشتات موجود است و می‌توانید از طریق linsel@geo.tu-darmstadt.de درخواست کنید. علاوه بر این، نمونه ها در سیستم ثبت نمونه زمین (SESAR، www.geosamples.org ) ثبت می شوند.
Ijgi 09 00409 g001 550
شکل ۱٫ مفهوم سازی یک متغیر منطقه ای شده پس از [ ۵ ] مثالی برای نفوذپذیری ذاتی نشان داده شده است.
Ijgi 09 00409 g002 550
شکل ۲٫ شماتیک اجزای عدم قطعیت ادغام شده در یک مدل پیش بینی خواص سنگ. ( الف ) تصویری از فرآیند درونیابی با استفاده از نقاط همسایه ایکسکبا مقادیر شناخته شده برای پیش بینی مقدار مجهول در ایکس۰. ( ب – د ) شماتیک توابع چگالی احتمال محلی (PDF) به شکل توزیع گاوسی که توسط σ۲و μبرای واریانس خطای کریجینگ تخمین زده شده است σاسک۲در ایکس۰( ب )، خطای اندازه گیری مشاهده شده σمتر۲در نقطه ایکس۳( ج ) و واریانس مشاهده شده σب۲در یک زیر مجموعه Ωباز Ω( د ).
Ijgi 09 00409 g003 550
شکل ۳٫ ( الف ) مدل فتوگرامتری معدن ماسه سنگ مورد بررسی. رخنمون توسط دو گسل قیچی تقسیم بندی شده و از دو توالی بوما دریاچه-دلتایی تشکیل شده است [ ۴۰ ]. ( ب ) بخش ۱-D رسوب شناسی از معماری رسوبی مشاهده شده در رخنمون. توالی بوما یک پایه فرسایشی را فراهم می کند. یک دنباله با یک روند رو به بالا مشخص می شود و شامل ماسه سنگ های عظیم غنی از داخل کلاس در پایه و ماسه سنگ های متقاطع بستر و موج دار به سمت بالا است [ ۴۰ ]. ( ج ) درونیابی فضایی یک نمونه PDF که با هر دو توزیع گاوسی نظری به دست آمده از اندازه‌گیری‌های OSB1_c و OSB2_c نشان داده شده است.
Ijgi 09 00409 g004 550
شکل ۴٫ ( الف ) مدل فتوگرامتری معدن ماسه سنگ مورد بررسی در Obersulzbach، آلمان. مکان های نمونه به صورت کره هایی نمایش داده می شوند که رنگ آنها مقدار نفوذپذیری مشاهده شده در مکان های نمونه را نشان می دهد. ( ب ) مش غیر متعامد شش وجهی رخنمون بررسی شده که توسط درون یابی IDW با استفاده از گره های مدل فتوگرامتری به عنوان محدودیت ایجاد می شود.
Ijgi 09 00409 g005 550
شکل ۵٫ مدل تجربی واریوگرام، هیستوگرام تجربی، و شاخص های ناهمگنی که از اندازه گیری های k برای رخنمون ( a – c )، و مکعب های سنگ OSB1_c ( d – f ) و OSB2_c ( g – i ) به دست آمده است. یک اثر مقیاس در ضریب تغییرات نشان‌دهنده ناهمگنی، ضریب Dykstra-Parson و واریانس نمونه قابل مشاهده است. همه مدل‌های واریوگرام با یک مدل کروی با اثر ناگت توصیف می‌شوند. مدل واریوگرام برای ( a ) با mD 0.05 = n توصیف شده است ۲a = 23 m و b = 0.75 mD ۲با n به عنوان قطعه، a به عنوان محدوده، و b به عنوان آستانه. مدل برای ( d ) با n = 0 mD توصیف شده است ۲a = 0.3 m و b = 0.58 mD ۲در حالی که مدل ( g ) با mD 0.005 = n توصیف شده است ۲a = 0.18 m و b = 0.08 mD ۲.
Ijgi 09 00409 g006 550
شکل ۶٫ توزیع فضایی نفوذپذیری ذاتی در مکعب سنگ OSB1_c ( a ) [ ۴۰ ] و OSB2_c ( b ) با استفاده از روش SK درونیابی شده است.
Ijgi 09 00409 g007 550
شکل ۷٫ ( الف ) نقشه برداری از واریانس محلی با توجه به ساختار زمین شناسی مشاهده شده. بیشترین واریانس با کره های قرمز و کمترین واریانس با کره های آبی نشان داده می شود. واریانس از اندازه‌گیری‌های مکعب سنگ OSB1_c – که نمایانگر ناهمگن‌ترین سنگ‌شناسی در پایین توالی‌های Bouma (قرمز) است – و OSB2_c – به همین ترتیب نشان‌دهنده همگن‌ترین سنگ‌شناسی در بالای توالی‌های Bouma (آبی) است. ( ب ) مدل واریانس محلی سه بعدی (LVM) که واریانس قابل مشاهده محلی را نشان می دهد، که توسط نگاشت های نشان داده شده در ( a ) محدود می شود.
Ijgi 09 00409 g008 550
شکل ۸٫ نتایج بهینه سازی برنامه ریزی اعداد صحیح خطی با استفاده از نقاط نمونه برداری مشخص شده. خطای درون یابی ϵآرماسEبا استفاده از قیود نابرابری ارائه شده در رابطه (۲۲) به حداقل می رسد. ( الف ) سطح پاسخ RMSE با توجه به واریانس خطای اندازه گیری گنجانده شده σمتر۲و حداکثر تعداد همسایگان nnبا استفاده از اعتبارسنجی متقاطع ترک یک خروجی. ( ب ) مقاطع عرضی از طریق سطح پاسخ ( a ).
Ijgi 09 00409 g009 550
شکل ۹٫ ( الف ) برآورد کریجینگ ساده ( b ) و واریانس کریجینگ ساده محلی برای یک تحقق SK.
Ijgi 09 00409 g010 550
شکل ۱۰٫ ( الف ) مقایسه هیستوگرام های تجربی σاسک۲مدل تولید شده در تحقق DSS با LVM و ( ب ) توزیع تجربی σاسک۲تولید شده در تحقق ( الف ).
Ijgi 09 00409 g011 550
شکل ۱۱٫ واریوگرام های تجربی (خاکستری) برای ۱۵ تحقق DSS ( a )، SGS ( b )، LVM-DSS ( c ) و LVM-SGS ( d ) همراه با میانگین تمام تحقق ها (آبی) و واریوگرام در نظر گرفته شده ترسیم شده اند. مدل (قرمز)، که توسط یک قطعه ۰٫۰۵ mD توصیف شده است ۲، برد ۲۳ متر و آستانه ۰٫۷۵ mD ۲.
Ijgi 09 00409 g012 550
شکل ۱۲٫ تجسم مدل نمونه برای تحقق DSS، SGS، LVM-DSS و LVM-SGS.
Ijgi 09 00409 g013 550
شکل ۱۳٫ نمای بالا بر روی یک نتیجه شبیه سازی نماینده DSS ( a ) و LVM-DSS ( b ) که توسط یک نمایش مقیاس خاکستری از LVM با کدورت ۰٫۶ روی هم قرار گرفته است. بدیهی است که ناهمگنی الگوریتم‌های مبتنی بر LVM در آن ناحیه از LVM که بالاترین واریانس محلی را نیز ارائه می‌کند، بالاترین است. رویکرد مرسوم، با این حال، واریانس مورد انتظار در فضا را منعکس نمی کند. ( ج ) تصویر مفهومی که توزیع فضایی اندازه‌گیری‌های محدودکننده را نشان می‌دهد ک(ایکسj)و رابطه فضایی بین برآورد کریجینگ ساده μاسکبا خطای اندازه گیری ϵمترو دو پارامتر مورد استفاده برای شبیه سازی k در این مطالعه یعنی σاسک۲و σLVم۲. Pr مخفف احتمال k تحت شرایطی است که k متعلق به توزیع گاوسی توصیف شده توسط μاسکهمراه با هر کدام σاسک۲یا σLVم۲.

ونوس نصیرفام

مقالات

فیسبوکتوئیترپینترسترددیتDeliciousلینکدینواتس اپتلگرامایمیل

نوشته های مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

خانهدربارهتماسارتباط با ما