شبکه پیچیدگی ابر نقطه ای بر اساس مکاتبات مکان مکانی

خلاصه

مطالعه شبکه های عصبی کانولوشن برای ابرهای نقطه سه بعدی به طور فزاینده ای محبوب می شود و مشکل عمدتاً در بی نظمی و بی نظمی ابرهای نقطه است. در حال حاضر، پیشنهاد یک عملیات کانولوشن و انجام اعتبارسنجی تجربی ساده است. اگرچه نتایج خوبی به دست آمده است، اما اصول پشت آنها توضیح داده نشده است – به عنوان مثال، چرا این می تواند بی نظمی و بی نظمی ابرهای نقطه ای را حل کند – و برای محققان دشوار است که یک شبکه کانولوشن ابر نقطه ای مناسب برای نیازهای خود طراحی کنند. برای این پدیده، ما یک چارچوب شبکه پیچیدگی نقطه‌ای را بر اساس مکاتبات مکان مکانی پیشنهاد می‌کنیم. پیروی از اصل مطابقت می تواند ما را در طراحی شبکه های کانولوشن متناسب با نیازهای ما راهنمایی کند. ما ماهیت ریاضی ذاتی عملیات پیچیدگی را تجزیه و تحلیل کردیم، و استدلال می‌کنیم که زمانی که تناظر مکان فضایی بین نقاط هسته کانولوشن و عناصر محدوده کانولوشن بدون تغییر باقی می‌ماند، عملیات پیچیدگی یکسان می‌ماند. با هدایت این اصل، ما یک چارچوب پیچیدگی نقطه کلی را بر اساس تناظر موقعیت مکانی فرموله کردیم، که توضیح می‌دهد چگونه یک ابر نقطه بی‌نظم را مدیریت کنیم. علاوه بر این، ما انواع مختلفی از مکاتبات را بر اساس موقعیت مکانی، از جمله روابط M-to-M، M-to-N، و M-to-1 و غیره مورد بحث قرار می‌دهیم که نحوه رسیدگی به بی‌نظمی ابرهای نقطه را توضیح می‌دهد. در نهایت، یک شبکه کانولوشن نقطه‌ای را مثال می‌زنیم که نقاط هسته پیچشی آن بر اساس توزیع ماتریس کوواریانس نمونه مطابق با چارچوب ما تولید می‌شوند. عملیات پیچیدگی ما را می توان در شبکه های مختلف پردازش ابری نقطه اعمال کرد. ما کارآمدی چارچوب خود را برای طبقه‌بندی ابر نقطه‌ای و وظایف تقسیم‌بندی معنایی، دستیابی به نتایج رقابتی با شبکه‌های پیشرفته نشان دادیم.

کلید واژه ها:

ابر نقطه سه بعدی ; شبکه پیچیدگی ; مکاتبات مکان مکانی ; طبقه بندی ; تقسیم بندی معنایی

۱٫ معرفی

درک صحنه سه بعدی (سه بعدی) با استفاده از یادگیری عمیق توجه روزافزونی را به خود جلب کرده است. توسعه سریع آن عمدتاً نتیجه نکات زیر است: (۱) راحتی دسترسی به حجم عظیمی از داده ها – از جمله مجموعه داده های منبع باز، مانند S3DIS [ ۱ ]، Semantic3D [ ۲ ]، یا SensatUrban [ ۳ ] —و توسعه حسگرها برای به دست آوردن داده ها (به عنوان مثال، LiDAR و پهپاد). (۲) توسعه دستگاه های سخت افزاری محاسباتی، مانند NVIDIA GPU [ ۴ ]، که می تواند حجم عظیمی از داده ها را به صورت موازی اداره کند. و (۳) چارچوب های یادگیری عمیق منبع باز، از جمله TensorFlow [ ۵ ]، PyTorch [ ۶ ]مطالعات بر روی درک صحنه سه بعدی شامل طبقه بندی و تقسیم بندی، تکمیل داده ها، تشخیص هدف سه بعدی، بازسازی سه بعدی، تقسیم بندی نمونه و غیره بوده است، اما به آنها محدود نشده است. این وظایف شامل طیف گسترده ای از کاربردهای عملی مانند چهره تشخیص، وسایل نقلیه خودمختار، ناوبری و موقعیت یابی ربات مستقل، فتوگرامتری، و سنجش از دور.

ابرهای نقطه سه بعدی به دلیل سادگی در نمایش دنیای سه بعدی واقعی محبوب هستند. آنها نمونه های گسسته ای از جهان طبیعی هستند که به صورت مختصات فضایی همراه با ویژگی های اضافی بسته به سبک اکتساب بیان می شوند. به عنوان مثال، ابرهای نقطه ای که با فناوری فتوگرامتری به دست می آیند، عموماً دارای اطلاعات رنگی هستند، در حالی که ابرهای به دست آمده توسط حسگرهای LiDAR دارای شدت و تعداد پژواک هستند. ابرهای نقطه‌ای نامنظم و بی‌نظم هستند که منجر به محدودیت‌هایی در کاربرد مستقیم عملیات پیچیدگی استاندارد برای ابرهای نقطه‌ای می‌شود. بی نظمی شکل هسته پیچیدگی کلاسیک را محدود می کند، در حالی که بی نظمی نحوه انجام عملیات پیچیدگی را محدود می کند.

تا به امروز، انواع شبکه‌های زیادی برای برخورد با ابرهای نقطه‌ای وجود دارد که نه تنها شامل روش‌های مبتنی بر کانولوشن [ ۷ ، ۸ ، ۹ ، ۱۰ ، ۱۱ ، ۱۲ ، ۱۳ ، ۱۴ ، ۱۵ ، ۱۶ ]، بلکه شامل MLP (پرسپترون چندلایه) نیز می‌شود. روش‌های مبتنی بر [ ۱۷ ، ۱۸ ]، مبتنی بر نمودار [ ۷ ، ۱۹ ، ۲۰ ] و حتی روش‌های مبتنی بر ترانسفورماتور [ ۲۱ ، ۲۲ ، ۲۳]. برخی از کارهای موجود، عملیات کانولوشن را در زمینه ابرهای نقطه ای مطالعه کرده اند [ ۸ ، ۱۰ ، ۱۱ ، ۱۶ ، ۲۴ ، ۲۵ ، ۲۶ ، ۲۷ .] و اجراهای امیدوارکننده ای به دست آوردند، اما بیشتر این آثار به سادگی یک شبکه پیچیدگی نقطه ای را پیشنهاد کردند و سپس آزمایش هایی را برای تأیید ایده های خود انجام دادند. آنها تجزیه و تحلیل عمیق تری از دلایلی ارائه نکردند که چرا این هسته ها و عملیات ها می توانند به عملیات پیچیدگی بر روی ابرهای نقطه دست یابند و بر بی نظمی و بی نظمی ابرهای نقطه غلبه کنند. اصل اساسی پشت این فرآیند هنوز آشکار نشده است. اگر بخواهیم آن را اصلاح کنیم تا نیازهایمان را برآورده کنیم، پیدا کردن مسیر درست برای بهبود آن دشوار است. به عنوان مثال، در Pointwise CNN [ ۱۱ ]، اگر بخواهیم سرعت را افزایش دهیم یا دقت را بهبود بخشیم، برای اصلاح پارامتر هسته کانولوشن آن چه باید بکنیم؟

برای پر کردن این شکاف، ما یک عملیات پیچیدگی نقطه‌ای قابل تفسیر بر اساس تطابق مکان مکانی پیشنهاد می‌کنیم و دلایلی را توضیح می‌دهیم که چرا این عملیات پیچیدگی می‌تواند به بی‌نظمی و بی‌نظمی ابرهای نقطه رسیدگی کند. پیروی از اصل تطابق می تواند ما را در طراحی شبکه های کانولوشن متناسب با نیازهای ما راهنمایی کند. در واقع، برخی از شبکه‌های کانولوشن موجود به طور بالقوه این اصل را گنجانده‌اند، اما به صراحت آن را توضیح و تحلیل نکرده‌اند. برای دستیابی به درک کامل، ما یک چارچوب پیچیدگی را بر اساس آن پیشنهاد می کنیم که شامل چندین مرحله تعیین کننده است. لازم به ذکر است که هدف ما طراحی شبکه کانولوشن خاصی برای ابرهای نقطه ای نبوده است. در عوض، ما بر روی یک چارچوب کانولوشن ابر نقطه‌ای کلی تمرکز کردیم که می‌تواند نیازهای مختلفی مانند دقت یا سرعت را برآورده کند. در راستای این چارچوب، ما یک عملیات پیچش ابر نقطه را توسعه دادیم و آزمایش‌های زیادی را روی طبقه‌بندی ابر نقطه و وظایف تقسیم‌بندی معنایی انجام دادیم. نتایج نشان داد که عملیات پیچیدگی در مقایسه با روش‌های پیشرفته به دقت ثابتی دست یافت.

کمک های اصلی ما به شرح زیر است:

(۱): ما ماهیت پیچیدگی گسسته را آشکار می کنیم – جمع محصولات بر اساس مکاتبات. آنچه مهم است مکاتبه است. ما معتقدیم که کانولوشن عملیاتی است که نه به ترتیب، بلکه به تناظر بین محدوده کانولوشن و هسته کانولوشن مربوط می شود. ما استدلال می کنیم که تا زمانی که مطابقت بین محدوده کانولوشن و عناصر موجود در یک هسته کانولوشن ثابت بماند، مقدار کانولوشن تغییر نمی کند.
(۲): ما دریافتیم که مکاتبات مکان مکانی ابرهای نقطه سه بعدی را برآورده می کند، که می تواند مشکل بی نظمی در ابرهای نقطه را حل کند. علاوه بر این، ما سبک های مختلف مکاتبات را تجزیه و تحلیل کردیم، و پیشنهاد می کنیم که ابرهای نقطه ای باید مطابقت های N-to-M را اتخاذ کنند، که می تواند مشکل بی نظمی در ابرهای نقطه را حل کند. اینها در سایر شبکه های کانولوشن موجود پوشش داده نمی شوند.
(۳): ما یک چارچوب کانولوشن کلی را برای ابرهای نقطه ای با توجه به مکاتبات مکان مکانی پیشنهاد می کنیم و نمونه ای از یک شبکه کانولوشن را بر اساس این چارچوب ارائه می دهیم. ما چندین آزمایش را روی وظایف ابر نقطه ای، مانند طبقه بندی و تقسیم بندی معنایی انجام دادیم. همه نتایج ما با شبکه های جریان اصلی فعلی سازگاری داشت.

۲٫ کارهای مرتبط

ابرهای نقطه ای، که در آن نقاط عنصر اساسی هستند، نمونه های گسسته ای از جهان عینی هستند که عموماً به صورت مجموعه ای از نقاط نمونه بیان می شوند. ابرهای نقطه ای معمولاً با مقادیر مختصات سه بعدی به اضافه سایر اطلاعات اضافی بسته به روش جمع آوری داده ها نشان داده می شوند – مانند مقادیر شدت و پژواک برای ابرهای نقطه ای از حسگرهای LiDAR یا اطلاعات رنگ برای فتوگرامتری. در این مقاله، ما عمدتا بر روی ابرهای نقطه ای با RGB تمرکز می کنیم.

ابرهای نقطه ای با بی نظمی، بی نظمی و چگالی ناهموار مشخص می شوند. تراکم ناهموار را می توان با استراتژی های نمونه گیری مختلف کاهش داد. به دلیل این بی نظمی و بی نظمی، پیچیدگی کلاسیک تصاویر را نمی توان مستقیماً روی ابرهای نقطه ای اعمال کرد. تحقیقات کنونی عمدتاً بر حل بی نظمی و بی نظمی ابرهای نقطه متمرکز شده است. روش های برخورد با ابرهای نقطه سه بعدی ممکن است مبتنی بر طرح ریزی، مبتنی بر MLP، مبتنی بر پیچیدگی، مبتنی بر گراف یا مبتنی بر ترانسفورماتور باشد.

۲٫۱٫ مبتنی بر فرافکنی

ایده اصلی روش‌های مبتنی بر پروجکشن این است که ابرهای نقطه‌ای را به‌عنوان داده‌های تنظیم‌شده نمایش دهند که می‌توان آن‌ها را به دو جنبه تقسیم کرد: مبتنی بر چند نمای و مبتنی بر وکسل.

۲٫۱٫۱٫ مبتنی بر چند نمایش

در تحقیقات قبلی، ابرهای نقطه‌ای ابتدا بر روی تصاویر دوبعدی چند نمای نمایش داده می‌شدند، و سپس از شبکه پیچیدگی بالغ روی تصویر برای پردازش تصویر پیش‌بینی‌شده استفاده می‌شد، پس از آن بر روی داده‌های سه‌بعدی پرتاب می‌شد. -view network [ ۲۸ ] عمل می کند. در فرآیند نمایش ابر نقطه سه بعدی بر روی یک تصویر دو بعدی، برخی از ابعاد و اطلاعات دقیق از بین رفته و دقت را کاهش می دهد.

۲٫۱٫۲٫ مبتنی بر وکسل

VoxNet [ ۹] و سایر ابزارها کانولوشن سه بعدی را روی داده های سه بعدی اعمال می کنند. این شبکه‌ها ابر نقطه سه‌بعدی را تنظیم می‌کنند و سپس اندازه‌های مختلف وکسل را برای نمایش شبکه وکسل در وضوح‌های مختلف تنظیم می‌کنند، معمولاً از مرکز نقطه واقع در وکسل برای نشان دادن مقدار آن وکسل استفاده می‌کنند. از آنجایی که ابر نقطه شامل داده هایی است که گسسته و پراکنده هستند، تعداد زیادی وکسل خالی به دست می آید که منجر به مقدار زیادی حافظه محاسباتی و کارایی هدر رفته می شود. هسته‌های کانولوشن سه‌بعدی در سه بعدی پیچیده می‌شوند، بنابراین کارایی محاسباتی آنها با تغییر در وضوح وکسل تغییر می‌کند. امروزه، اندازه هسته کانولوشن ۳ بعدی مبتنی بر وکسل معمولاً ۳۲ × ۳۲ × ۳۲ یا ۶۴ × ۶۴ × ۶۴ است. این رویکرد برای پردازش داده‌های عمومی LiDAR، مانند داده‌های ابری نقطه‌ای LiDAR برای رانندگی خودکار استفاده می‌شود.

۲٫۲٫ مبتنی بر نقطه

PointNet [ ۱۷ ] در کاربرد مستقیم MLP برای نقاط پیشگام بود، و کارهای بعدی بسیاری از جمله PointNet++ [ ۱۸ ] و غیره دنبال شد. اطلاعاتی که به دست می‌آورد، اطلاعات سراسری و تک نقطه‌ای است – نه اطلاعات محلی. با این حال، همه ما می دانیم که اطلاعات محلی نقش مهمی در طبقه بندی و تقسیم بندی اشیاء ایفا می کند، همانطور که CNN ها می توانند ساختار محلی را ضبط کنند و نتایج خوبی روی تصاویر به دست آورند. کار بعدی بر اساس PointNet بر چگونگی دستیابی به درک بهتر از همسایگان محلی تمرکز دارد.

۲٫۳٫ مبتنی بر نمودار

این رویکرد ابر نقطه ای را به عنوان یک ساختار داده گراف می سازد و سپس از شبکه های عصبی گراف برای پردازش داده های سه بعدی استفاده می کند. شبکه های خاص عبارتند از ECC [ ۱۹ ]، DGCNN [ ۷ ] و SPG [ ۲۰ ]]، که در طبقه بندی و تقسیم بندی ابرهای نقطه نیز به نتایج خوبی دست یافته اند، در حالی که DGCNN به نتایج عالی در ساخت پویا ساختارهای داده گراف بر اساس ویژگی های استخراج شده از هر لایه دست یافته است. SPG عمدتاً برای حل مشکل مقیاس بزرگ با ابتدا تقسیم بندی بیش از حد ابرهای نقطه و سپس ساخت ساختارهای نمودار ابرنقطه برای بلوک های ابر نقطه تقسیم شده طراحی شده است. پس از آن، جاسازی از PointNet به شبکه عصبی گراف وارد می‌شود، که بهتر می‌تواند با مشکل ابرهای نقطه‌ای صحنه‌های بزرگ مقابله کند.

۲٫۴٫ مبتنی بر پیچیدگی

گزینه اعمال عملیات کانولوشن به طور مستقیم روی ابرهای نقطه ای نیز مورد توجه قرار گرفته است. هدف اصلی آنها غلبه بر بی‌نظمی و بی‌نظمی ابرهای نقطه‌ای، گرفتن ویژگی‌های محلی، و استخراج بهتر ویژگی‌های ابرهای نقطه‌ای برای خدمت به طیف گسترده‌ای از اهداف پایین دست است. این شامل دو جنبه اصلی است: یکی پرداختن به اختلال با یادگیری یک تبدیل هم ترازی، مانند PointCNN [ ۱۰ ]، که هدف آن یادگیری یک ماتریس X است که وظیفه تبدیل ترتیب نقاط همسایگی را دارد تا پیچیدگی های بعدی انجام شود. عملیات را می توان به عنوان مستقل از سفارش در نظر گرفت.

روش دیگر، رویکرد مبتنی بر هسته است که مستقیماً کانولوشن را اعمال می‌کند، از جمله روش‌های نقطه هسته مانند KPConv [ ۸ ] و روش‌های bin-kernel مانند Pointwise CNN [ ۱۱ ]. اساساً، هر دو به روش‌های نقطه هسته تعلق دارند، اما دامنه متفاوتی برای تأثیرگذاری بر فضا دارند. محتوای اصلی این مقاله یک کانولوشن مبتنی بر هسته نقطه است.

بر اساس چارچوب پیشنهادی کانولوشن ابر نقطه ای نشان داده شده در شکل ۱ ، هر مرحله از انتخاب های مختلف، عملیات پیچیدگی متفاوتی را تولید می کند. ما رابطه بین چارچوب کانولوشن خود و عملیات انحراف نقطه ای موجود را تجزیه و تحلیل کردیم و به این نتیجه رسیدیم که مورد دوم نمونه هایی از چارچوب پیچیدگی ما را در برخی موارد خاص نشان می دهد. شبکه‌های کانولوشن زیر همگی به طور بالقوه اصل اصلی تطابق مکان مکانی را در خود جای داده‌اند، اما هسته‌های پیچشی متفاوت بیان می‌شوند:

در PointNet [ ۱۷ ]، با توجه به چارچوب کانولوشن ابر نقطه، وقتی از سیستم همسایگی به تنهایی استفاده می کنیم (یعنی فقط یک نقطه)، هسته کانولوشن نیز تنها یک نقطه دارد که مختصات مکان مکانی برای آن (۰) است. ، ۰، ۰). پس از ایجاد مکاتبات بر اساس موقعیت مکانی اقلیدسی، حداکثر ادغام (یعنی MLP مشترک که عملیات PointNet [ ۱ ] نیز نامیده می شود) روی نقاط اعمال می شود.

CNN نقطه‌ای [ ۱۱ ] ابر نقطه‌ای را به شبکه‌های فضایی تقسیم می‌کند، یک MLP مشترک را برای نقاط درون هر زیرشبکه اعمال می‌کند، و سپس روی تمام زیرشبکه‌ها تکرار می‌کند تا آنها را جمع کند، و به نوعی عملیات جمع کانولوشن دست می‌یابد. سیستم همسایگی آن یک سیستم k-NN است، و هسته کانولوشن یک وکسل مکعبی است، که در آن هر وکسل فرعی در یک هسته می‌تواند به عنوان یک مکان و یک مکعب از محدوده نفوذ در نظر گرفته شود.

برای PointConv [ ۲۶ ]، که از k-NN به عنوان سیستم همسایگی استفاده می کند، هسته آن بر اساس نقاط هسته تولید شده نیست. این بیشتر شبیه یک مکانیسم توجه با در نظر گرفتن رمزگذاری مکان ها است.

برای SPH3D [ ۲۷ ]، که سیستم همسایگی آن مبتنی بر شعاع است، هسته آن اساساً بر اساس تناظر فضایی است، و هر سطل در یک هسته کروی را می توان به عنوان یک مکان و یک محدوده تأثیر در نظر گرفت.

برای ۳DGCN [ ۲۹ ]، که سیستم همسایگی آن مبتنی بر شعاع است، هسته آن بر اساس مکاتبات مکان مکانی است که اطلاعات جهت را در نظر می گیرد.

KPConv [ ۸ ] بر اساس یک پیچیدگی هسته نقطه برای پردازش ابرهای نقطه با استفاده از یک نقطه هسته مولد است، و همچنین می تواند عملیات کانولوشن قابل تغییر شکل را طراحی کند، که هر دو به نتایج خوبی دست یافته اند. این یک سیستم همسایه مبتنی بر شعاع ایجاد می‌کند، و هسته کانولوشن – تابعی از بهینه‌سازی نقاط منظم در کره – مطابقت را با مکان فضایی اقلیدسی برقرار می‌کند.

۲٫۵٫ مبتنی بر ترانسفورماتور

ترانسفورماتور در ابتدا برای حل مشکلات NLP مورد استفاده قرار گرفت. اکنون کاربردهای زیادی برای مشکلات بینایی دارد که در آنها عملکرد خوبی داشته است. همچنین برای ابرهای نقطه سه بعدی، به عنوان مثال، توسط Point Transformer [ ۲۱ ]، Point Transformer [ ۲۲ ] و PCT [ ۲۳ ] اعمال شده است. تبدیل ترکیبی از توجه و MLP بر اساس ساختار محاسباتی منحصر به فرد آن است که می تواند ساختارهای داده نامرتب و با طول متغیر را مدیریت کند و به خوبی برای داده هایی مانند ابرهای نقطه ای مناسب است. با این حال، کاربرد خاص آن برای ابرهای نقطه‌ای به تحقیقات بیشتری نیاز دارد.

۳٫ مواد و روشها

تمرکز اصلی این مطالعه بر روی پردازش مستقیم ابرهای نقطه با RGBRGB در یک عملیات کانولوشن یادگیری عمیق است. این بخش نحوه تعمیم شبکه های کانولوشن استاندارد را به ابرهای نقطه ای توضیح می دهد. به پنج بخش فرعی تقسیم شده است. در بخش ۳٫۱ ، ماهیت ریاضی ذاتی عملیات انحراف را تجزیه و تحلیل می‌کنیم و استدلال می‌کنیم که نتیجه کانولوشن زمانی که مطابقت مکان مکانی بین نقاط هسته کانولوشن و عناصر محدوده کانولوشن بدون تغییر باقی می‌ماند، ثابت می‌ماند. در بخش ۳٫۲، سپس سبک های مکاتبات مختلف را بر اساس تناظرهای مکان مکانی، از جمله N-to-N، N-to-M، N-to-1 و غیره تجزیه و تحلیل می کنیم و سبک N-to-M را برای ابرهای نقطه ای اتخاذ می کنیم. تطابق مکان مکانی می تواند اختلال را برطرف کند و روابط N-to-M به بی نظمی ابرهای نقطه ای می پردازد. در بخش ۳٫۳ ، با توجه به این استدلال، ما یک چارچوب پیچیدگی ابر نقطه ای را فرموله می کنیم که می تواند مستقیماً برای آدرس دادن به ابرهای نقطه سه بعدی اعمال شود، که مطابقت های مکان مکانی را در نظر می گیرد و می تواند مشکلات بی نظمی و بی نظمی در ابرهای نقطه را حل کند.

ابتدا، ما با تجزیه و تحلیل عملیات ریاضی کانولوشن روی تصاویر دو بعدی شروع می کنیم و به این نتیجه می رسیم که ماهیت کانولوشن روی داده های مکانی این است که اطمینان حاصل شود که مطابقت مکان مکانی بین نقاط هسته کانولوشن و عناصر پیچیدگی بدون تغییر باقی می ماند. به طور کلی، ما هسته کانولوشن را روی یک تصویر به عنوان یک ماتریس با شکل خاصی از پارامترهای تعبیه شده در نظر می گیریم که دارای یک نقطه بحرانی است که به راحتی نادیده گرفته می شود، یعنی وجود مکان هایی که در آن کانولوشن انجام می شود. به دلیل تنظیم تصویر، مطابقت ذاتی بین هسته ها و پنجره های پیچشی وجود دارد. در مورد ابرهای نقطه ای، تنها کاری که باید انجام دهیم این است که این مطابقت را در ابر نقطه اعمال کنیم. سپس راهی پیدا می کنیم که این مطابقت را بر اساس فاصله فضایی اقلیدسی بر روی ابرهای نقطه ای ثابت کنیم. ما می توانیم مختصات فضایی را به عناصر موجود در هسته کانولوشن اختصاص دهیم و سپس محدوده تأثیرگذاری آن را با توجه به فاصله اقلیدسی تعیین کنیم. پس از ایجاد مکاتبات مکان مکانی، می‌توانیم عملیات کانولوشن را روی ابر نقطه انجام دهیم، زیرا این عملیات می‌تواند با حفظ ویژگی‌های کانولوشن، بی‌نظمی و بی‌نظمی ابرهای نقطه را کنترل کند.

با تعریف کانولوشن ابر نقطه ای، می توانیم خط لوله شبکه کانولوشن خود را برای پردازش یک ابر نقطه فرموله کنیم. ابتدا یک سیستم همسایگی برای ابرهای نقطه ای تعیین می کنیم (در این مطالعه از سیستم همسایگی شعاع استفاده می کنیم). سپس هسته کانولوشن را انتخاب می کنیم، از جمله روشی که در آن نقاط هسته کانولوشن ایجاد می شوند و شکل هسته کانولوشن (ما نقاط هسته را از یک ماتریس کوواریانس برای نمونه تولید می کنیم). در نهایت، ما عملیات پیچیدگی را با توجه به مکاتبات مکان مکانی انجام می دهیم. شکل ۱ کل خط لوله را توصیف می کند.

۳٫۱٫ ماهیت ریاضی پیچیدگی

فرمول ریاضی برای کانولوشن پیوسته ۱ بعدی به شرح زیر است:

f∗gn=🔻-∞∞f(τ)g(n-τ)دτ،

(۱)

جایی که fو gتوابع پیچیدگی درگیر هستند، nمحدوده پیچیدگی است، τعنصر در عملکرد است fدر محدوده پیچیدگی n، و (n-τ)عنصر مطابقت در تابع کانولوشن است g.

فرمول کانولوشن گسسته دو بعدی روی تصاویر به شرح زیر است:

f∗gمن،j=∑متر∑nf(متر،n)g(من-متر،j-n)،

(۲)

جایی که fتصویر دو بعدی است، gهسته کانولوشن است، من،jمحدوده پیچیدگی را بیان می کند، (متر،n)عنصر پیچیدگی را در تابع بیان می کند fدر محدوده پیچیدگی من،j، و (من-متر،j-n)عنصر مطابقت در هسته کانولوشن است g.

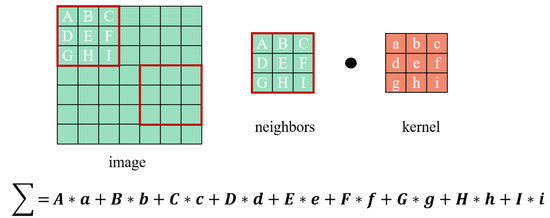
به عنوان مثال، یک کانولوشن تصویر یک کانال، یک عملیات نامتقارن از ضرب عناصر مربوطه و جمع کردن محصول است. به دلیل منظم بودن داده های تصویر که دارای نظم طبیعی هستند، وقتی سیستم همسایگی را تعریف می کنیم، همیشه برای یک پیکسل تعداد همسایه های یکسانی وجود خواهد داشت. عناصر محدوده کانولوشن با ضرب نقطه به نقطه با پارامترهای روی هسته کانولوشن بر اساس مطابقت و سپس جمع کردن محصولات، همانطور که در شکل ۲ نشان داده شده است، شروع می شود .

اجازه دهید به مورد ابرهای نقطه نگاه کنیم. شکل ۳ بی نظمی و بی نظمی یک ابر نقطه سه بعدی را نشان می دهد. سمت چپ شکل ۳ ابر نقطه اصلی یک شی را نشان می‌دهد که می‌توانیم یک سیستم همسایگی شعاع را شناسایی کنیم. کادر مشکی خط چین در وسط نشان دهنده بی نظمی ابر نقطه با تعداد نقاط مختلف و توزیع ناهموار در همان محله است. کادر سبز رنگ در سمت راست نشان دهنده بی نظمی ابر نقطه است که N تعداد ابرهای نقطه ای است که می توان دید N دارد! جایگشت ها

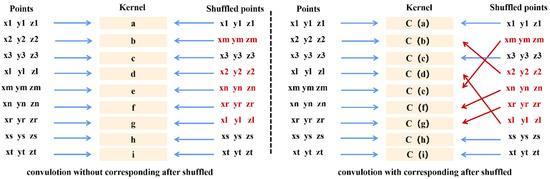
وقتی می خواهیم پیچیدگی استاندارد را روی یک ابر نقطه اعمال کنیم، اولین مشکل ناشی از بی نظمی آن است. یک سیستم همسایگی تعداد نقاط متفاوتی در مناطق مختلف دارد، به این معنی که ما نمی توانیم اندازه هسته کانولوشن را تعیین کنیم. حال فرض می کنیم با روش نمونه گیری به همان تعداد امتیاز در همسایگی به دست می آوریم. سپس می توان اندازه هسته کانولوشن را به عنوان تعداد نقاط با اندازه همسایگی مشخص تعیین کرد که موقعیت های مختلف عنصر هسته کانولوشن دارای پارامترهای متفاوتی خواهد بود. مشکل دوم ناشی از بی نظمی آن است، زیرا همان ابرهای نقطه ای N متفاوتی دارند! جایگشت. در شکل ۴، (x1، y1، z1) مختصات نقطه، a نقطه هسته بدون مطابقت، و C(a) نقطه هسته با مطابقت است. در سمت چپ شکل ۴، برای عنصر b در هسته، نقطه (x2, y2, z2) در دنباله اصلی b را با توجه به مطابقت پیش فرض نشان می دهد. هنگامی که ابر نقطه طبق ترتیب دیگری به هم می‌ریزد، نقطه (x2، y2، z2) نشان‌دهنده d، در حالی که نقطه (xm، ym، zm) نشان‌دهنده b است. این باید مقداری متفاوت از آنچه که قبلاً پس از ضرب و جمع کردن عملیات به دست آمد، به دست آورد. با استفاده از یک هسته کانولوشن قطعی و طبق کانولوشن استاندارد، N را به دست خواهیم آورد! مقادیر مختلف پیچیدگی، که نتیجه مورد نظر ما نیست. حتی اگر N داشته باشیم! جایگشت، پس از یک عملیات کانولوشن، ما همیشه می خواهیم همان نتیجه را به دست آوریم. شکل ۴ عملیات کانولوشن را برای نقاط مخلوط شده توضیح می دهد.

برای حفظ مقادیر کانولوشن ثابت، باید مطابقت بین عناصر در محدوده کانولوشن و عناصر موجود در هسته کانولوشن را ثابت نگه داریم. در پانل سمت راست شکل ۴ ، f(1) یک رابطه مطابقت بین اولین عنصر در هسته و نقاط را نشان می دهد. هنگامی که این مطابقت برقرار شد، نقطه (x2، y2، z2) همیشه b را نشان می دهد، حتی اگر ترتیب به هم ریخته باشد. همه اینها برای یافتن مطابقت در ابرهای نقطه و در نتیجه حل مشکل بی نظمی ضروری است.

اکنون به مشکل بی نظمی بازگردیم.

ما می توانیم یک تصویر را به عنوان مثال برای تجزیه و تحلیل انواع مختلف تناظر بین محدوده کانولوشن و هسته کانولوشن بگیریم ( شکل ۵ ). برای اینکه بعداً اصل را به ابرهای نقطه‌ای بسط دهیم، می‌توانیم تصویر را بر اساس ستون و موقعیت شاخص پیکسل بازآرایی کنیم. پانل بالایی در شکل تصویر اصلی است. پانل پایین تصویر سازماندهی مجدد شده است. در پانل سمت چپ شکل، N-به-N پیچیدگی استاندارد تصویر را نشان می دهد، که در آن موقعیت های مختلف مقادیر پارامترهای متفاوتی دارند. اگر همه مقادیر در هسته کانولوشن یکسان باشند، این معادل یک مقدار یکسان است که می تواند به عنوان یک مطابقت N-به-۱ دیده شود. شکل ۴انواع مکاتبات را نشان می دهد. به دلیل بی نظمی، باید از مکاتبات N-to-M برای پردازش ابر نقطه استفاده کنیم. در این مرحله، نامنظمی ابرهای نقطه نیز حل می شود.

به طور خلاصه، فرمول کانولوشن گسسته به صورت زیر فرموله می شود:

(f∗g)(ک)=∑من=۰من∑j=0jf(من)من∈ن(ک)*g(j)j∈هستهψ(من،j)=سی،

(۳)

جایی که کعنصر پیچیدگی مورد بررسی است، من∈ن(ک)یعنی که منیک نقطه همسایه است کدر یک سیستم همسایه، jعنصری است که به هسته کانولوشن تعلق دارد و ψ(من،j)=سینشان میدهد که منو jباید یک محدودیت را برآورده کند – که به آن رابطه مکاتبات نیز گفته می شود.

را کدر فرمول (۳) می تواند نه تنها داده های ۱ بعدی، بلکه داده های ۲ بعدی و با ابعاد بالاتر را نیز نمایش دهد. چه زمانی کنشان دهنده داده های ۱ بعدی، رابطه مطابقت است ψ(من،j)=سیراضی می کند من+j=nو بنابراین، فرمول (۳) را می توان برای کانولوشن گسسته یک بعدی، مشابه فرمول (۱) استفاده کرد. چه زمانی کداده های ۲ بعدی مانند یک تصویر را نشان می دهد (س،تی)، در این مورد، مناست (متر،n)و jاست (پ،q); بنابراین، رابطه مکاتبه ψ(من،j)=سیراضی می کند [متر+پ=س،n+q=تی]همانطور که در فرمول (۲) توضیح داده شده است. چه زمانی کیک ابر نقطه سه بعدی را نشان می دهد که می تواند به صورت نمایش داده شود (ایکس،y،z)، مناست (ل،متر،n)و jاست (r،س،تی). بنابراین ما باید پیدا کنیم ψ(من،j)=سیبرای یک ابر نقطه

۳٫۲٫ مکاتبات مکان مکانی

در پرتو این درک از ابرهای نقطه ای، ما از تناظرهای موقعیت مکانی به عنوان داده های مکانی استفاده کردیم. از تناظرهای مبتنی بر موقعیت مکانی اقلیدسی می توان برای ایجاد مطابقت ابرهای نقطه ای استفاده کرد. ما می توانیم نقاط مختصات فضایی عناصر را در هسته کانولوشن اختصاص دهیم، که می تواند توسط توابع مختلف تولید شود. همسایگان نقاط هسته کانولوشن در محدوده پیچیدگی تعیین می شوند، به این معنی که نقاط در محدوده کانولوشن همیشه مطابقت بدون تغییر خواهند داشت. نقاط همسایه یک نقطه هسته پیچیدگی این مطابقت را برآورده می کند. مهم نیست که ترتیب جایگشت آنها چگونه تغییر می کند، مطابقت این همسایه هرگز تغییر نمی کند، بنابراین مقدار کانولوشن نهایی ثابت می ماند. این مکاتبات مبتنی بر موقعیت مکانی اقلیدسی می تواند مشکل بی نظمی در ابرهای نقطه سه بعدی را حل کند و در ترکیب با استراتژی تطابق N-to-M، می تواند بی نظمی ابرهای نقطه سه بعدی را نیز حل کند. بنابراین، می‌توانیم عملیات پیچیدگی را تعمیم داده و آن را در ابرهای نقطه‌ای اعمال کنیم.شکل ۶ مطابقت‌های مبتنی بر مکان‌های فضایی اقلیدسی را در ابرهای نقطه‌ای سه‌بعدی، که برای راحتی توسط دایره‌ها نشان داده شده‌اند، توصیف می‌کند.

۳٫۳٫ چارچوب پیچیدگی نقطه

بر اساس بحث بالا، می‌توانیم یک چارچوب پیچیدگی کلی ایجاد کنیم که می‌تواند برای ابرهای نقطه‌ای اعمال شود. شکل ۱ یک چارچوب پیچیدگی کلی را برای ابرهای نقطه ای توصیف می کند.

برای ابرهای نقطه سه بعدی، می‌توانیم یک عملیات پیچیدگی ابر نقطه خاص را طبق چارچوب پیشنهادی از طریق مراحل زیر شناسایی کنیم:

(۱): ابتدا یک سیستم محله ابر نقطه ای مناسب را تعیین کنید.
(۲): دوم، نحوه ایجاد نقاط مختصات هسته کانولوشن و اندازه مناسب هسته کانولوشن را تعیین کنید. در این مطالعه، ما نقاط هسته را از ماتریس کوواریانس یک نمونه تولید کردیم.
(۳): سوم، محدوده تأثیر هر یک از نقاط هسته پیچیدگی را بر اساس مکان فضایی اقلیدسی تعیین کنید.
(۴): در نهایت عمل کانولوشن را طبق مکاتبات اعمال کنید.

۳٫۴٫ نمونه ای از یک شبکه

به عنوان نمونه ای از عملیات کانولوشن برای ابرهای نقطه ای بر اساس تجزیه و تحلیل بالا، ما یک شبکه با استفاده از چارچوب رمزگذار-رمزگشا ساختیم. ما از محله شعاع استفاده کردیم. مطالعه قبلی [ ۳۰ ] نشان داده است که سیستم همسایگی مبتنی بر شعاع نمایش بهتری در ابرهای نقطه ای دارد. ما انتخاب کردیم که نقاط هسته کانولوشن را با توجه به ماتریس کوواریانس نمونه ها تولید کنیم، جایی که هر لایه دارای هسته متفاوتی با توجه به ماتریس کوواریانس نمونه ها بود. هر لایه از معماری ResNet با نمونه‌گیری شبکه‌ای برای ادغام استفاده می‌کرد. ماژول های کانولوشن و ادغام هر دو یک بلوک ResNet استاندارد داشتند. شکل ۷ لایه های کانولوشن و ادغام را توضیح می دهد.

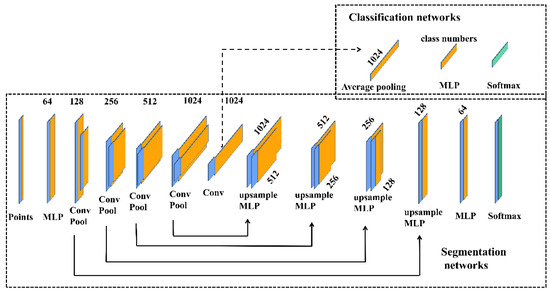
پانل پایین بلوک عملیات ادغام است. D _in و D _out به ترتیب ابعاد ویژگی ورودی و ابعاد ویژگی خروجی را در لایه جاری نشان می دهند. در این مطالعه، ما انتخاب کردیم که نقاط هسته پیچشی را با توجه به ماتریس کوواریانس نمونه‌ها ایجاد کنیم. شکل ۸ معماری کلی شبکه را شرح می دهد.

۴٫ نتایج و بحث

ما آزمایش‌های انبوهی را برای تأیید ایده‌های خود انجام دادیم، از جمله وظایف طبقه‌بندی و تقسیم‌بندی معنایی برای ابرهای نقطه سه بعدی. همه کارها روی پردازنده گرافیکی NVIDIA Tesla V100 32 گیگابایتی آزمایش شدند. همه آزمایش ها از بهینه ساز Adam استفاده کردند. روش افزایش ما شامل پوسته پوسته شدن، چرخاندن و نویز کردن نقاط بود. تعداد نقاط هسته در همه آزمایش‌ها ۱۳ بود مگر اینکه خلاف آن ذکر شده باشد.

۴٫۱٫ وظایف طبقه بندی

طبقه بندی ModelNet40

ما مدل خود را روی کار طبقه‌بندی ModelNet40 [ ۳۱ ] آزمایش کردیم. مجموعه داده ModelNet40 شامل ابرهای نقطه شی مصنوعی است. به عنوان پرکاربردترین معیار برای تجزیه و تحلیل ابر نقطه، ModelNet40 به دلیل دسته بندی های مختلف، اشکال تمیز، مجموعه داده های خوب و غیره محبوب است. مجموعه داده اصلی ModelNet40 از ۱۲۳۱۱ مش تولید شده توسط CAD در ۴۰ دسته (مانند هواپیما، اتومبیل) تشکیل شده است. ، گیاهان و لامپ ها) که از این تعداد ۹۸۴۳ مورد برای آموزش استفاده شده است، در حالی که ۲۴۶۸ مورد دیگر برای آزمایش در نظر گرفته شده است. نقاط داده ابر نقطه متناظر به طور یکنواخت از سطوح مش نمونه برداری شد و سپس با حرکت به مبدا و مقیاس بندی در یک کره واحد پیش پردازش شد.

ما تقسیم‌بندی‌های آموزشی/آزمایشی استاندارد را دنبال کردیم و اشیاء را مجدداً اندازه‌گیری کردیم تا آنها را در یک کره واحد قرار دهیم. ما نرمال ها را نادیده گرفتیم، زیرا فقط داده های مصنوعی در دسترس بود. اندازه نمونه اول ۰٫۰۲ متر بود و هر لایه بعدی دو برابر اندازه لایه قبلی نمونه برداری شد. شعاع هسته کانولوشن اندازه نمونه لایه فعلی ضرب در پارامتر چگالی بود، که عدد ثابتی بود که آن را روی ۵ قرار دادیم. اندازه دسته ۳۲ و نرخ یادگیری ۰٫۰۰۱ بود. مومنتوم برای عادی سازی دسته ای ۰٫۹۸ بود.

جدول ۱ نتایج طبقه بندی شکل سه بعدی را نشان می دهد. شبکه های نشان داده شده در جدول شامل شبکه های طبقه بندی ابر نقطه سه بعدی موجود در حال حاضر می باشد. مدل کوواریانس ما به ۹۲٫۷ درصد دقت کلی دست یافت – تا ۳٫۵ درصد بیشتر از PointNet [ ۱۷ ]، و ۰٫۲ درصد کمتر از KPConv [ ۸ ] که بهترین نتیجه را داشت، همانطور که در جدول ۱ نشان داده شده است. این روش کوواریانس به ما این امکان را داد که برازش بهتری با توزیع داده ها داشته باشیم و ویژگی های هدفمند بیشتری را بیاموزیم. شکل ۹ منحنی ضرر را نشان می دهد.

۴٫۲٫ وظایف تقسیم بندی معنایی

تقسیم بندی معنایی با استفاده از سه مجموعه داده آزمایش شد: S3IDS [ ۱ ]، Semantic3D [ ۲ ] و SensatUrban [ ۳ ].

۴٫۲٫۱٫ S3DIS: تقسیم بندی معنایی برای صحنه های داخلی

ما مدل خود را بر روی مجموعه داده S3DIS برای یک کار تقسیم بندی صحنه معنایی ارزیابی کردیم. این مجموعه داده شامل ابرهای نقطه اسکن سه بعدی برای شش منطقه داخلی است که در مجموع ۲۷۲ اتاق را شامل می شود. هر نقطه به ۱ از ۱۳ دسته معنایی (به عنوان مثال، تخته، قفسه کتاب، صندلی، سقف، تیر و غیره) به اضافه درهم و برهم تعلق دارد.

در آزمایش، هر نقطه به عنوان یک بردار ۹ بعدی (XYZ، RGB، و مختصات فضایی نرمال شده) نشان داده شد. مناطق آموزش مناطق ۱، ۲، ۳، ۴ و ۶ و منطقه آزمایش منطقه ۵ بود. نمونه شعاع ورودی ۱ متر بود. اندازه نمونه اول ۰٫۰۴ متر بود و هر لایه بعدی دو برابر اندازه لایه قبلی نمونه برداری شد. شعاع هسته کانولوشن اندازه نمونه لایه فعلی ضرب در پارامتر چگالی بود که عدد ثابتی بود که آن را روی ۵ قرار دادیم. اندازه دسته ۱۲ و نرخ یادگیری ۰٫۰۱ بود. مومنتوم برای عادی سازی دسته ای ۰٫۹۸ بود. ما نقاط هسته را با استفاده از ماتریس کوواریانس نمونه ها تولید کردیم. شکل ۱۰ نتایج تقسیم بندی معنایی را برای ناحیه ۵ نشان می دهد.

جدول ۲ معیارها را در مقایسه با سایر شبکه ها شرح می دهد. مدل ما در مقایسه با سایر مدل‌های نشان‌داده‌شده در جدول، بهترین mIOU (64.6%) و میانگین کلاس دقت (۶۹٫۶%) را به دست می‌آورد، به جز اینکه فقط کمی کمتر از KPConv [ ۸ ] است.

۴٫۲٫۲٫ Semantic3D: LiDAR Semantic Segmentation

Semantic3D [ ۲ ] مجموعه داده ابر نقطه ای از صحنه های فضای باز اسکن شده با بیش از ۳ میلیارد نقطه است. این شامل ۱۵ آموزش و ۱۵ صحنه آزمایشی است که به عنوان هشت کلاس شرح داده شده است. این مجموعه داده ابر نقطه سه بعدی بزرگ، طبیعی و دارای برچسب، طیف وسیعی از مناظر شهری متنوع از جمله کلیساها، خیابان ها، خطوط راه آهن و میادین را پوشش می دهد.

برای بررسی عملکرد شبکه خود بر روی داده‌های LiDAR بدون اطلاعات رنگ، دو مدل را با این مجموعه داده آموزش دادیم: یکی با داده‌های LiDAR رنگی، که به عنوان XYZRGB نشان داده می‌شود. و یکی بدون داده های رنگی که فقط XYZ را نشان می دهد. به دلایلی ناشناخته، معیار Semantic3D [ ۳۵ ] مدتی است که قادر به ارزیابی مجموعه تست نیست و ما فقط می‌توانیم نتایج بصری مجموعه تست را ارائه دهیم. با این حال، ما تجسم و ارزیابی مجموعه اعتبار سنجی را ارائه کردیم، و تقسیم مجموعه داده های اعتبارسنجی به دنبال KPConv [ ۸ ] بود.

در آزمایش با رنگ، هر نقطه به عنوان یک بردار ۹ بعدی (XYZ، RGB، و مختصات فضایی نرمال شده) نشان داده شد. در آزمایش بدون رنگ، هر نقطه به عنوان یک بردار ۶ بعدی (XYZ و مختصات فضایی نرمال شده) نشان داده شد و پارامتر دیگر یکسان بود. مجموعه داده آموزشی مورد استفاده ما شامل داده های رسمی ارائه شده بود. ما از داده های کاهش یافته-۸ برای آزمایش استفاده کردیم. نمونه شعاع ورودی ۳ متر بود. اندازه نمونه اول ۰٫۰۶ متر بود و هر لایه بعدی دو برابر اندازه لایه قبلی نمونه برداری شد. شعاع هسته کانولوشن اندازه نمونه لایه فعلی ضرب در پارامتر چگالی بود که عدد ثابتی بود که آن را ۵ قرار دادیم. اندازه دسته ۱۶ و نرخ یادگیری ۰٫۰۱ بود. مومنتوم برای عادی سازی دسته ای ۰٫۹۸ بود.شکل ۱۱ نتایج تقسیم بندی معنایی را برای داده های کاهش یافته-۸ با/بدون رنگ نشان می دهد. با توجه به نتایج تجسم، تفاوت کمی بین مدل رنگی و مدل غیر رنگی وجود داشت. تجزیه و تحلیل ما نشان داد که اشیاء صحنه ساختمان‌ها، خیابان‌ها، وسایل نقلیه و غیره هستند.

جدول ۳ جزئیات معیارها را در مقایسه با شبکه های دیگر در ۸ کاهش یافته با مدل رنگی توضیح می دهد. مدل ما به mIOU 75.5% دست یافت و صحنه های طبیعی و اتومبیل ها بهترین دقت کلاس را به دست آوردند. از آنجایی که معیار Semantic3D [ ۳۵ ] در حال حاضر به دلایل ناشناخته نمی تواند نتایج مجموعه آزمایشی را ارائه دهد، ما نتوانستیم ارزیابی متریک مدل غیر رنگی را ارائه دهیم، اما نتایج تجسم و ارزیابی متریک مجموعه اعتبار سنجی را ارائه کردیم، همانطور که نشان داده شده است. در شکل ۱۲ و جدول ۴ به ترتیب.

۴٫۲٫۳٫ SensatUrban: مجموعه داده های ابر نقطه فتوگرامتری در سطح شهر

مجموعه داده SensatUrban [ ۳ ] یک مجموعه داده ابر نقطه فتوگرامتری در مقیاس شهری با نزدیک به ۳ میلیارد نقطه با حاشیه نویسی غنی است. مجموعه داده شامل مناطق بزرگی از دو شهر بریتانیا است که حدود ۶ کیلومتر مربع ^از چشم انداز شهر را پوشش می دهد. در مجموعه داده، هر نقطه ۳ بعدی به عنوان یکی از ۱۳ کلاس معنایی (به عنوان مثال، زمین، پوشش گیاهی، اتومبیل، و غیره) برچسب گذاری شده است.

در آزمایش، هر نقطه به عنوان یک بردار ۹ بعدی (XYZ، RGB، و مختصات فضایی نرمال شده) نشان داده شد. مجموعه داده های آموزشی و آزمایشی که ما استفاده کردیم با مجموعه داده های SensatUrban [ ۳ ] سازگار بود. نمونه شعاع ورودی ۵ متر بود. اندازه نمونه اول ۰٫۱ متر بود و هر لایه بعدی دو برابر اندازه لایه قبلی نمونه برداری شد. شعاع هسته کانولوشن اندازه نمونه لایه فعلی ضرب در پارامتر چگالی بود که عدد ثابتی بود که آن را ۵ قرار دادیم. اندازه دسته ۱۶ و نرخ یادگیری ۰٫۰۱ بود. مومنتوم برای عادی سازی دسته ای ۰٫۹۸ بود. ما نقاط هسته را با استفاده از ماتریس کوواریانس نمونه ها تولید کردیم. شکل ۱۳ نتایج تقسیم بندی معنایی را برای SensatUrban نشان می دهد.

جدول ۵ معیارهای تقسیم بندی معنایی دقیق را برای SensatUrban شرح می دهد. مدل ما به mIOU 56.92% دست یافت.

۴٫۳٫ بحث

ما دو عامل کلیدی را برای آزمایش تأثیر آنها بر نتایج انتخاب کردیم: روشی که در آن نقاط هسته تولید شدند و تعداد نقاط هسته.

۴٫۳٫۱٫ روشی که در آن نقاط هسته ایجاد شد

ما اثرات طبقه‌بندی روش‌های مختلف تولید هسته، یعنی ماتریس کوواریانس نمونه‌ها و روش تصادفی را مقایسه کردیم. اولی نقاط هسته را با توجه به ماتریس کوواریانس نمونه ها تولید می کند. دومی نقاط هسته را از نقاط تصادفی در یک کره واحد تولید می کند.

در جدول ۱ ، می بینیم که حتی روش تصادفی دقت ۹۱٫۵ تا ۲٫۳% بیشتر از PointNet [ ۱۷ ] و کمتر از ۱٫۲% کمتر در مقایسه با کوواریانس دارد – بنابراین ما معتقدیم که نقاط هسته به طور تصادفی تولید شده ممکن است با آن مطابقت نداشته باشند. داده ها. این نشان می دهد که نقاط هسته سازگار با توزیع داده ها ممکن است برای بیان بهتر آموخته شوند. این ما را تشویق می‌کند تا یک نقطه هسته کانولوشن ایجاد کنیم که با داده‌ها بیشتر مطابقت داشته باشد، که جهتی برای کار آینده ما است.

۴٫۳٫۲٫ تعداد نقاط هسته

ما یک آزمایش مقایسه ای بر روی اثر و زمان برای تعداد مختلف نقاط هسته در یک کار تقسیم بندی معنایی با مجموعه داده S3DIS انجام دادیم. نقاط هسته پیچشی از ماتریس کوواریانس نمونه ها ایجاد شد. شکل ۱۴ نتایج را نشان می دهد.

همانطور که در شکل ۱۲ نشان داده شده است ، mIOU زمانی که تعداد نقاط هسته ۱۳ بود به حداکثر خود رسید و بیش از این تعداد به بهبود ادامه نداد. همانطور که انتظار می رفت، با افزایش تعداد امتیازات، زمان افزایش یافت. این به ما می گوید که اگر سرعت را دنبال می کنیم، باید تعداد هسته ها را کاهش دهیم، در حالی که اگر به دنبال دقت هستیم، باید تعداد نقاط هسته را افزایش دهیم که باید بر اساس نیاز خود تعادل ایجاد کنیم. لازم به ذکر است که بسته به مجموعه داده های مختلف، تراکم نمونه، ساختار چارچوب و تعداد لایه ها، تعداد بهینه نقاط هسته کانولوشن ثابت نیست.

۵٫ نتیجه گیری ها

در این کار، ما یک چارچوب پیچشی پیشنهاد می‌کنیم که می‌تواند مستقیماً برای ابرهای نقطه‌ای اعمال شود و مطابقت‌های موقعیت مکانی را در نظر بگیرد. ما ماهیت ریاضی کانولوشن را تجزیه و تحلیل کردیم و دریافتیم که تا زمانی که مطابقت ها بدون تغییر باقی می مانند، عملیات پیچیدگی بدون تغییر باقی می ماند. علاوه بر این، انواع روابط مطابقت را بر اساس مکان و تأثیر تعداد و روش تولید نقاط هسته مورد بحث قرار دادیم. ما شبکه کانولوشن خود را از طریق کارهای طبقه بندی و تقسیم بندی معنایی تأیید کردیم. بر اساس نتایج، تناظرهای موقعیت مکانی پیشنهادی ما برای ابرهای نقطه ای قابل استفاده است. این می تواند به عنوان یک اصل برای راهنمایی ما در طراحی شبکه های کانولوشن ابر نقطه ای که نیازهای متنوع ما را برآورده می کند، استفاده شود. همراه با چارچوب، ما فقط نیاز به ایجاد مراحل جداگانه برای ایجاد یک شبکه قطعی برای دستیابی به یک برنامه پردازش ابری نقطه ای سریع یا با دقت بالا داریم. این به ما کمک می کند تا به جای تلاش برای طراحی ماژول های شبکه پیچیده و نامفهوم، روی چگونگی حل کل مشکل تمرکز کنیم.

در این مقاله، ما عمدتا بر روی ابرهای نقطه ای با رنگ تمرکز می کنیم. با این حال، همانطور که همه ما می دانیم، همه ابرهای نقطه ای رنگ ندارند – برای مثال، ابرهای نقطه لیدار. بررسی روش پیچیدگی پیشنهادی روی ابرهای نقطه‌ای بدون رنگ، تمرکز کار بعدی ما خواهد بود. در همین حال، ما معتقدیم که چارچوب ما می‌تواند به انواع داده‌های بیشتر تعمیم داده شود – نه فقط ابرهای نقطه‌ای یا تصاویر – و همچنین برای پردازش مشترک تصاویر و ابرهای نقطه‌ای، به شرطی که مطابقت مناسبی پیدا کنیم.

منابع

ارمنی، من. سنر، او. ضمیر، ع. جیانگ، اچ. بریلاکیس، آی. فیشر، ام. Savarese, S. تجزیه معنایی سه بعدی فضاهای داخلی در مقیاس بزرگ. در مجموعه مقالات کنفرانس IEEE 2016 در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، لاس وگاس، NV، ایالات متحده آمریکا، ۲۷ تا ۳۰ ژوئن ۲۰۱۶؛ IEEE: لاس وگاس، NV، ایالات متحده؛ صص ۱۵۳۴-۱۵۴۳٫ [ Google Scholar ]
هاکل، تی. ساوینوف، ن. لدیکی، ال. Wegner، JD; شیندلر، ک. Pollefeys، M. Semantic3D. Net: معیار طبقه بندی ابر نقطه ای جدید. arXiv ۲۰۱۷ , arXiv:1704.03847. [ Google Scholar ]
هو، کیو. یانگ، بی. خالد، س. شیائو، دبلیو. تریگونی، ن. مارکهام، A. به سوی تقسیم بندی معنایی ابرهای نقطه سه بعدی در مقیاس شهری: مجموعه داده، معیارها و چالش ها در مجموعه مقالات کنفرانس IEEE/CVF 2021 در مورد دید رایانه و تشخیص الگو (CVPR)، نشویل، TN، ایالات متحده، ۲۰-۲۵ ژوئن ۲۰۲۱؛ IEEE: نشویل، TN، ایالات متحده؛ صفحات ۴۹۷۵-۴۹۸۵٫ [ Google Scholar ]
رهبری محاسبات هوش مصنوعی از NVIDIA. در دسترس آنلاین: https://www.nvidia.com/en-us/ (در ۱۸ ژوئیه ۲۰۲۲ قابل دسترسی است).
TensorFlow. در دسترس آنلاین: https://tensorflow.google.cn/?hl=en (در ۱۸ ژوئیه ۲۰۲۲ قابل دسترسی است).
PyTorch. در دسترس آنلاین: https://pytorch.org/ (در ۱۸ ژوئیه ۲۰۲۲ قابل دسترسی است).
Wang, Y. DGCNN: نمایش‌های ابر نقطه یادگیری توسط دینامیک گراف CNN. Ph.D. پایان نامه، موسسه فناوری ماساچوست، کمبریج، MA، ایالات متحده آمریکا، ۲۰۲۰٫ [ Google Scholar ]
توماس، اچ. Qi، CR; Deschaud, J.-E.; مارکوتگی، بی. گولت، اف. Guibas، LJ KPConv: پیچش انعطاف پذیر و تغییر شکل پذیر برای ابرهای نقطه ای. در مجموعه مقالات کنفرانس بین المللی IEEE/CVF در بینایی رایانه (ICCV)، سئول، جمهوری کره، ۲۷ اکتبر تا ۲ نوامبر ۲۰۱۹٫ [ Google Scholar ]
ماتورانا، دی. Scherer, S. VoxNet: یک شبکه عصبی کانولوشن سه بعدی برای تشخیص اشیاء در زمان واقعی. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2015 در مورد ربات ها و سیستم های هوشمند (IROS)، هامبورگ، آلمان، ۲۸ سپتامبر تا ۳ اکتبر ۲۰۱۵؛ ص ۹۲۲-۹۲۸٫ [ Google Scholar ]
لی، ی. بو، ر. سان، م. وو، دبلیو. دی، ایکس. چن، بی. پوینت سی ان ان: پیچیدگی در نقاط تبدیل شده X. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی، ونکوور، BC، کانادا، ۸ تا ۱۴ دسامبر ۲۰۱۹؛ Curran Associates, Inc.: Red Hook, NY, USA, 2018; جلد ۳۱٫ [ Google Scholar ]
Hua، B.-S.; تران، M.-K. یونگ، اس.-کی. شبکه های عصبی کانولوشنال نقطه ای در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ IEEE: سالت لیک سیتی، UT، ایالات متحده آمریکا؛ ص ۹۸۴-۹۹۳٫ [ Google Scholar ]
تاتارچنکو، م. پارک، جی. کلتون، وی. ژو، Q.-Y. پیچش های مماس برای پیش بینی متراکم در سه بعدی. arXiv ۲۰۱۸ , arXiv:1807.02443. [ Google Scholar ]
وانگ، اس. سو، اس. ما، W.-C. پوکروفسکی، آ. Urtasun، R. شبکه های عصبی کانولوشن پیوسته پارامتریک عمیق. در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ صص ۲۵۸۹–۲۵۹۷٫ [ Google Scholar ]
Deuge، MD; کوادروس، ا. هونگ، سی. Douillard, B. آموزش ویژگی بدون نظارت برای طبقه بندی اسکن های سه بعدی در فضای باز. در مجموعه مقالات کنفرانس استرالیایی در مورد رباتیک و اتوماسیون، سیدنی، استرالیا، ۲ تا ۴ دسامبر ۲۰۱۳٫ [ Google Scholar ]
هو، کیو. یانگ، بی. زی، ال. رزا، اس. گوا، ی. وانگ، ز. تریگونی، ن. مارکهام، A. RandLA-Net: تقسیم بندی معنایی کارآمد ابرهای نقطه ای در مقیاس بزرگ. در مجموعه مقالات کنفرانس IEEE/CVF در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، سیاتل، WA، ایالات متحده آمریکا، ۱۳ تا ۱۹ ژوئن ۲۰۲۰٫ [ Google Scholar ]
گراهام، بی. انگلک، م. van der Maaten، L. تقسیم‌بندی معنایی سه بعدی با شبکه‌های کانولوشنال پراکنده زیرمنیفولد. در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ IEEE: سالت لیک سیتی، UT، ایالات متحده آمریکا؛ ص ۹۲۲۴–۹۲۳۲٫ [ Google Scholar ]
Qi، CR; سو، اچ. مو، ک. Guibas، LJ PointNet: یادگیری عمیق در مجموعه های نقطه برای طبقه بندی و تقسیم بندی سه بعدی. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، هونولولو، HI، ایالات متحده آمریکا، ۲۱ تا ۲۶ ژوئیه ۲۰۱۷٫ [ Google Scholar ]
Qi، CR; یی، ال. سو، اچ. Guibas، LJ PointNet++: یادگیری ویژگی های سلسله مراتبی عمیق در مجموعه های نقطه در یک فضای متریک. Adv. عصبی Inf. روند. سیستم ۲۰۱۷ ۳۰ . _ [ Google Scholar ]
سیمونوفسکی، م. کوموداکیس، N. فیلترهای شرطی لبه پویا در شبکه های عصبی کانولوشن روی نمودارها. در مجموعه مقالات کنفرانس IEEE 2017 در مورد دید رایانه و تشخیص الگو (CVPR)، هونولولو، HI، ایالات متحده آمریکا، ۲۱ تا ۲۶ ژوئیه ۲۰۱۷؛ ص ۲۹-۳۸٫ [ Google Scholar ]
لندریو، ال. Simonovsky، M. تقسیم بندی معنایی ابر نقطه ای بزرگ با نمودارهای ابرنقطه ای. در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ صص ۴۵۵۸–۴۵۶۷٫ [ Google Scholar ]
گوو، ام.-اچ. کای، جی. لیو، Z.-N. مو، تی.-جی. مارتین، آر. Hu, S. PCT: Point Cloud Transformer. تعریف نشده ۲۰۲۱ ، ۷ ، ۱۸۷-۱۹۹٫ [ Google Scholar ] [ CrossRef ]
ژائو، اچ. جیانگ، ال. جیا، جی. تور، پی. کلتون، ترانسفورماتور V. Point. در مجموعه مقالات کنفرانس IEEE/CVF در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، سیاتل، WA، ایالات متحده آمریکا، ۱۳ تا ۱۹ ژوئن ۲۰۲۰٫ [ Google Scholar ]
انگل، ن. بلاگیانیس، وی. Dietmayer، K. Point Transformer. دسترسی IEEE ۲۰۲۱ ، ۹ ، ۱۳۴۸۲۶–۱۳۴۸۴۰٫ [ Google Scholar ] [ CrossRef ]
گرو، اف. ویشولک، پی. Lensch، HPA Flex-Convolution (Million-Scale Point-Cloud Learning Beyond Grid-Worlds). arXiv ۲۰۲۰ ، arXiv:1803.07289. [ Google Scholar ]
لی، اچ. اختر، ن. Mian، A. Octree CNN را با هسته های کروی برای ابرهای نقطه سه بعدی هدایت می کند. در مجموعه مقالات کنفرانس IEEE/CVF 2019 در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، ۱۵ تا ۲۰ ژوئن ۲۰۱۹؛ IEEE: لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا؛ صص ۹۶۲۳–۹۶۳۲٫ [ Google Scholar ]
وو، دبلیو. چی، ز. Fuxin، L. PointConv: شبکه‌های پیچیده عمیق در ابرهای نقطه سه بعدی. در مجموعه مقالات کنفرانس IEEE/CVF در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، سیاتل، WA، ایالات متحده آمریکا، ۱۳ تا ۱۹ ژوئن ۲۰۲۰٫ [ Google Scholar ]
لی، اچ. اختر، ن. Mian، A. هسته کروی برای پیچیدگی نمودار کارآمد در ابرهای نقطه سه بعدی. IEEE Trans. الگوی مقعدی ماخ هوشمند ۲۰۲۱ ، ۴۳ ، ۳۶۶۴-۳۶۸۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
سو، اچ. مجی، س. کالوگراکیس، ای. Learned-Miller, E. شبکه های عصبی کانولوشنال چند نمای برای تشخیص شکل سه بعدی. در مجموعه مقالات کنفرانس بین المللی IEEE 2015 در بینایی کامپیوتر (ICCV)، سانتیاگو، شیلی، ۷ تا ۱۳ دسامبر ۲۰۱۵؛ ص ۹۴۵-۹۵۳٫ [ Google Scholar ]
لین، ز.-اچ. هوانگ، S.-Y. Wang, Y.-CF Convolution in the Cloud: Learning Kernels Deformable in 3D Graph Convolution Networks for Point Cloud Analysis. در مجموعه مقالات کنفرانس IEEE/CVF 2020 در مورد دید رایانه و تشخیص الگو (CVPR)، سیاتل، WA، ایالات متحده آمریکا، ۱۳ تا ۱۹ ژوئن ۲۰۲۰؛ صفحات ۱۷۹۷-۱۸۰۶٫ [ Google Scholar ]
توماس، اچ. گولت، اف. Deschaud, J.-E.; مارکوتگی، بی. LeGall، Y. طبقه‌بندی معنایی ابرهای نقطه‌ای سه‌بعدی با همسایگی‌های کروی چند مقیاسی. در مجموعه مقالات کنفرانس بین المللی ۲۰۱۸ در ۳D Vision (3DV)، ورونا، ایتالیا، ۵-۸ سپتامبر ۲۰۱۸؛ صص ۳۹۰-۳۹۸٫ [ Google Scholar ]
وو، زی. آهنگ ها.؛ خسلا، ع. یو، اف. ژانگ، ال. تانگ، ایکس. Xiao, J. ShapeNets 3D: A Deep Representation for Volumetric Shapes. در مجموعه مقالات کنفرانس IEEE 2015 در مورد بینایی کامپیوتری و تشخیص الگو (CVPR)، بوستون، MA، ایالات متحده آمریکا، ۷ تا ۱۲ ژوئن ۲۰۱۵؛ IEEE: بوستون، MA، ایالات متحده آمریکا؛ صفحات ۱۹۱۲-۱۹۲۰٫ [ Google Scholar ]
لی، جی. چن، BM; لی، GH SO-Net: شبکه خودسازماندهی برای تحلیل ابر نقطه ای. در مجموعه مقالات کنفرانس IEEE/CVF 2018 در مورد دید رایانه و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ ص ۹۳۹۷–۹۴۰۶٫ [ Google Scholar ]
خو، ی. فن، تی. خو، ام. زنگ، ال. Qiao, Y. SpiderCNN: یادگیری عمیق در مجموعه های نقطه با فیلترهای کانولوشن پارامتری شده. در مجموعه مقالات کنفرانس اروپایی بینایی کامپیوتر (ECCV)، مونیخ، آلمان، ۸ تا ۱۴ سپتامبر ۲۰۱۸٫ [ Google Scholar ]
چاپمی، ال. چوی، سی. ارمنی، من. گواک، جی. Savarese, S. SEGCloud: Semantic Semmentation of 3D Point Clouds. در مجموعه مقالات کنفرانس بین المللی ۲۰۱۷ در ۳D Vision (3DV)، چینگدائو، چین، ۱۰-۱۲ اکتبر ۲۰۱۷؛ صص ۵۳۷-۵۴۷٫ [ Google Scholar ]
Semantic3D. در دسترس آنلاین: http://semantic3d.net/ (در ۱۶ نوامبر ۲۰۲۲ قابل دسترسی است).

شکل ۱٫ چارچوب کانولوشن ابرهای نقطه سه بعدی: بخش بالایی تعریف چارچوب پیچیدگی کلی را ارائه می دهد. بخش پایین پیچیدگی را طبق این مطالعه توصیف می کند. داشتن انتخاب های مختلف برای عناصر موجود در کادر قرمز رنگ، عملیات پیچیدگی متفاوتی را ایجاد می کند.

شکل ۲٫ پیچیدگی یک تصویر: پانل بالایی همسایگان و اندازه هسته کانولوشن را روی تصویر نشان می دهد. جعبه قرمز محدوده پیچیدگی است، جامد سیاه عملیات پیچش است. فرمول پایین روش محاسبه پیچش گسسته تصویر را توصیف می کند.

شکل ۳٫ بی نظمی و بی نظمی یک ابر نقطه سه بعدی: ابر نقطه در سمت چپ نشان داده شده است. کادر مشکی چین وسط، بی نظمی ابر نقطه سه بعدی را با شعاع همسایه r، تعداد نقاط مختلف (m و n) و توزیع های مختلف نشان می دهد. کادرهای سبز رنگ در سمت راست هر دو بی نظمی ابر نقطه سه بعدی را نشان می دهند، جایی که همان ابر نقطه دارای n است! دستورات مختلف، هر چند آنها یک موجودیت را بیان می کنند.

شکل ۴٫ عملیات کانولوشن برای نقاط مخلوط شده با و بدون تناظر: (x1، y1، z1) مختصات نقطه، a نقطه هسته بدون مطابقت، و C(a) نقطه هسته با مطابقت است. پانل سمت چپ نشان می دهد که پیچش بدون مطابقت پس از زدن نتیجه متفاوتی ایجاد می کند. پانل سمت راست نشان می دهد که برای عملیات کانولوشن با متناظر پس از به هم زدن نقاط، نقاط درهم ریخته همیشه همان پارامتر را نشان می دهند و نتیجه بدون تغییر است.

شکل ۵٫ انواع مکاتبات برای کانولوشن گسسته: مطابقت N-به-N پیچیدگی تصویر استاندارد را توصیف می کند. اگر پارامترها در همه مکان ها یکسان باشند از N-to-1 استفاده می شود. دایره سیاه عمل کانولوشن است، فلش متناظر است. انواع مکاتبات دیگری نیز وجود دارد، به عنوان مثال، N-to-M، و غیره.

شکل ۶٫ مطابقت های مبتنی بر مکان های فضایی اقلیدسی در ابرهای نقطه سه بعدی. دایره سمت چپ محدوده انحراف را در یک سیستم همسایه شعاع نشان می دهد، که در آن نقطه نارنجی نقطه پیچش و نقاط در دایره آبی نقطه چین همسایگان آن هستند. دایره میانی نقاط هسته کانولوشن تولید شده توسط یک تابع خاص را نشان می دهد. این نقاط دارای مختصات فضایی سه بعدی خواهند بود. دایره سمت راست روابط مطابقت را بر اساس موقعیت مکانی اقلیدسی توصیف می کند.

شکل ۷٫ لایه های کانولوشن و ادغام. پانل بالایی بلوک عملیات کانولوشن است.

شکل ۸٫ معماری کلی شبکه: ستون فقرات از معماری رمزگذار – رمزگشا و اتصال پرش استفاده می کند. شاخه بالایی شبکه های طبقه بندی را نشان می دهد. شاخه پایین شبکه های تقسیم بندی معنایی را نشان می دهد.

شکل ۹٫ منحنی ضرر برای طبقه بندی ModelNet40.

شکل ۱۰٫ نتایج تقسیم بندی معنایی ناحیه ۵: پانل بالایی داده های RGB خام را نشان می دهد. پانل وسط حقیقت زمین است. پانل پایین پیش بینی ها را نشان می دهد.

شکل ۱۱٫ نتایج تقسیم بندی معنایی برای داده های کاهش یافته-۸: ستون سمت چپ داده های اصلی را نشان می دهد. ستون وسط نتایج پیش بینی شده را با رنگ نشان می دهد. ستون سمت راست نتایج پیش بینی شده را بدون رنگ نشان می دهد.

شکل ۱۲٫ نتایج تقسیم بندی معنایی برای داده های اعتبارسنجی: پانل بالایی داده های اصلی را نشان می دهد. پانل پایینی نتیجه پیش بینی شده است.

شکل ۱۳٫ نتایج تقسیم بندی معنایی برای SensatUrban: ردیف های اول و سوم داده های اصلی را نشان می دهند. ردیف های دوم و چهارم نتایج پیش بینی شده را نشان می دهند.

شکل ۱۴٫ mIOU و زمان تقسیم بندی معنایی برای تعداد مختلف نقاط هسته.