GisGCN: چارچوبی مبتنی بر نمودار بصری برای تطبیق مناطق جغرافیایی در طول زمان

منابع بصری تاریخی به ویژه برای بازسازی حالات متوالی قلمرو در گذشته و برای تحلیل تحولات آن مفید هستند. با این حال، یافتن منابع بصری که یک منطقه معین را در انبوهی از آرشیوها پوشش می‌دهند، اگر مستند ضعیفی داشته باشند، می‌تواند بسیار دشوار باشد. در مورد عکس های هوایی، این کار در بیشتر مواقع صرفاً با تکیه بر محتوای بصری تصاویر انجام می شود. شبکه‌های عصبی کانولوشنال می‌توانند نشانه‌های بصری تصاویر را ضبط کرده و با توجه به داده‌های آموزشی کافی، آنها را با یکدیگر تطبیق دهند. با این حال، در طول زمان و در طول فصول، مناظر طبیعی و مصنوعی ممکن است تکامل پیدا کنند و بازیابی تصاویر تاریخی را به یک کار چالش برانگیز تبدیل کنند. ما می خواهیم به این مشکل نمایه سازی و بازیابی هوایی متقاطع از دیدگاه جدید متفاوتی بپردازیم: با استفاده از ویژگی‌های هندسی و توپولوژیکی موجودیت‌های جغرافیایی منطقه مورد تحقیق که به‌عنوان نمایش گراف کدگذاری شده‌اند که نسبت به تغییرات ظاهری قوی‌تر از نمونه‌های مبتنی بر تصویر خالص هستند. موجودات جغرافیایی در تصاویر هوایی عمودی به عنوان گره هایی در یک نمودار در نظر گرفته می شوند که توسط یال هایی که روابط فضایی آنها را نشان می دهند به یکدیگر مرتبط می شوند. برای ساخت چنین نمودارهایی، ما استفاده از نمونه‌هایی از پایگاه‌های داده برداری توپوگرافی و روش‌های پیشرفته تحلیل فضایی را پیشنهاد می‌کنیم. ما نشان می‌دهیم که چگونه این نمودارهای جغرافیایی را می‌توان با موفقیت در طول زمان با استفاده از جاسازی گراف آموخته شده مطابقت داد. موجودات جغرافیایی در تصاویر هوایی عمودی به عنوان گره هایی در یک نمودار در نظر گرفته می شوند که توسط یال هایی که روابط فضایی آنها را نشان می دهند به یکدیگر مرتبط می شوند. برای ساخت چنین نمودارهایی، ما استفاده از نمونه‌هایی از پایگاه‌های داده برداری توپوگرافی و روش‌های پیشرفته تحلیل فضایی را پیشنهاد می‌کنیم. ما نشان می‌دهیم که چگونه این نمودارهای جغرافیایی را می‌توان با موفقیت در طول زمان با استفاده از جاسازی گراف آموخته شده مطابقت داد. موجودات جغرافیایی در تصاویر هوایی عمودی به عنوان گره هایی در یک نمودار در نظر گرفته می شوند که توسط یال هایی که روابط فضایی آنها را نشان می دهند به یکدیگر مرتبط می شوند. برای ساخت چنین نمودارهایی، ما استفاده از نمونه‌هایی از پایگاه‌های داده برداری توپوگرافی و روش‌های پیشرفته تحلیل فضایی را پیشنهاد می‌کنیم. ما نشان می‌دهیم که چگونه این نمودارهای جغرافیایی را می‌توان با موفقیت در طول زمان با استفاده از جاسازی گراف آموخته شده مطابقت داد.

کلید واژه ها:

منابع تصویری تاریخی ; تعبیه گراف ; توصیفگرهای جغرافیایی ; نمایه سازی و بازیابی داده های تاریخی

۱٫ مقدمه

منابع بصری تاریخی، مانند نقشه‌ها، حکاکی‌ها، نقاشی‌ها یا عکس‌ها، تنها بازنمایی‌های بصری قلمرو جغرافیایی گذشته هستند که هنوز در دسترس هستند. به این ترتیب، آنها منابع اطلاعاتی بسیار مهمی برای تجزیه و تحلیل قلمرو گذشته و تکامل آن هستند. در سال‌های اخیر، بسیاری از ابتکارات سیستم اطلاعات جغرافیایی (GIS) با استفاده از نقشه‌ها یا به ندرت از عکس‌های قدیمی برای بازسازی قلمرو گذشته توسعه یافته‌اند.

اولین چالشی که این آثار با آن مواجه هستند، ارجاع جغرافیایی منابع بصری تاریخی است. هدف این عملیات تعیین موقعیت جغرافیایی یک منبع بصری معین است. این می تواند با استفاده از یک مدل حسگر فیزیکی مبتنی بر اطلاعات فیزیکی و هندسی دقیق که حسگر مورد استفاده برای ضبط داده را توصیف می کند یا یک مدل مطابقت مشتق شده از مجموعه ای از نقاط کنترل زمینی که مختصات زمین و تصویر برای آنها مشخص است، انجام شود [ ۱ ]. چه به صورت دستی [ ۲ ] و چه به صورت خودکار [ ۳]، این کار مستلزم ارائه نقاط کنترل زمینی کافی به سیستمی است که مدل ارجاع جغرافیایی را تخمین می زند. بنابراین، این امر مستلزم شناسایی از قبل منطقه تحت پوشش هر منبع بصری تاریخی است، که در مورد عکس‌های هوایی قدیمی، که گاهی مستندات بسیار ضعیفی دارند، می‌تواند بسیار دشوار باشد.

چالش دوم در استخراج اطلاعات مفید از منابع بصری و ادغام آنها در یک ساختار داده GIS برای قابل استفاده کردن آنها نهفته است. به عنوان مثال، نام مکان های باستانی را می توان از نقشه های قدیمی استخراج کرد و با مکان های مربوطه در برخی از فرمت های داده GIS ذخیره کرد. این عملیات را می توان به صورت دستی، اغلب از طریق رویکردهای مشترک انجام داد (به عنوان مثال، https://geo.nls.uk/maps/gb1900/ (در ۲۸ اکتبر ۲۰۲۱ قابل دسترسی است) یا https://geohistoricaldata.org/ ) (دسترسی شده است) در ۲۸ اکتبر ۲۰۲۱)، یا به صورت نیمه خودکار، با استفاده از ابزارهای تصحیح یا اعتبارسنجی مشارکتی (مانند http://buildinginspector.nypl.org/(دسترسی در ۲۸ اکتبر ۲۰۲۱))، روی داده‌های تولید شده توسط روش‌های تقسیم‌بندی خودکار تصویر و بردارسازی اعمال شد [ ۴ ، ۵ ].

کار ارائه شده در این مقاله به چالش فوق‌الذکر می‌پردازد، یعنی شناسایی و فهرست‌بندی خودکار منطقه جغرافیایی تحت پوشش برخی منابع بصری تاریخی. ما به‌ویژه روی عکس‌های هوایی قدیمی تمرکز می‌کنیم، اما این رویکرد می‌تواند به منابع بصری دیگر مانند نقشه‌های قدیمی نیز تعمیم یابد. ما این کار را گامی به سوی چارچوب یکپارچه برای تجزیه و تحلیل منابع چند بعدی چند بعدی می بینیم.

روش‌های موجود طراحی‌شده برای تطبیق با یک عکس هوایی معمولاً سپس آن را با پایگاه‌داده‌ای از عکس‌های زمین مرجع [ ۶ ] با استفاده از نشانه‌های بصری، یعنی رنگ، بافت یا توصیفگرهای درخشندگی مقایسه می‌کنند. با این حال، به دلیل تغییرات ساختاری و ظاهری که در طول زمان اتفاق می‌افتد، تطبیق عکس‌های هوایی موجود در طول سال‌ها کار ساده‌ای نیست. ساختمان‌ها و جاده‌های جدید ظاهر می‌شوند، ساختمان‌های قدیمی تخریب می‌شوند، رودخانه‌ها و جوی‌های آب می‌توانند بستر خود را تغییر دهند، و غیره. در روز کسب

در حالی که رویکرد ما تطبیق تصویر هوایی تاریخی با عکس‌های جغرافیایی مرجع را هدف قرار می‌دهد، ما یک روش اساسی متفاوت و جدید را برای رمزگذاری اطلاعات گرفته‌شده توسط عکس‌ها پیشنهاد می‌کنیم: ما پیشنهاد می‌کنیم که از ویژگی‌های هندسی (محیط عادی و خروج از مرکز، شکل، هم‌نشینی، و غیره) و توپولوژیکی استفاده کنیم. موجودیت های جغرافیایی که به جای نشانه های بصری خالص با عکس ها نشان داده می شوند. در واقع، ما فکر می‌کنیم که استفاده از ویژگی‌ها و روابط فضایی موجودیت‌های جغرافیایی می‌تواند از رویکردهای تطبیق مبتنی بر نشانه‌های بصری بهتر عمل کند، زیرا آنها در طول زمان کمتر از ظاهر بصری عکس‌ها تغییر می‌کنند. برای استفاده از این ویژگی‌های موجودات جغرافیایی، اولین قدم استخراج آنها از عکس‌ها، با استفاده از ابزارهای برداری خودکار است. با این حال، برای آزمایش فرضیه ما، پیشنهاد می کنیم ابتدا این مرحله را کنار بگذاریم و به جای آن از نمونه هایی از پایگاه داده های جغرافیایی برداری استفاده کنیم. در واقع، پایگاه‌های اطلاعاتی توپوگرافی برداری مدرن معمولاً از عکس‌های هوایی گرفته می‌شوند و بنابراین از نظر هندسی با آنها سازگار هستند. از این رو، با الهام از پیشرفت اخیر در یادگیری بر روی داده های گراف، ما پیشنهاد می کنیم صحنه ای را که یک منطقه جغرافیایی را به عنوان یک نمودار نشان می دهد، مدل کنیم، که یک راه بسیار قدرتمند و شهودی برای رمزگذاری اطلاعات جغرافیایی است. در این نمودار، موجودیت‌های جغرافیایی توسط گره‌ها نشان داده می‌شوند، ویژگی‌های آن‌ها به عنوان برچسب به گره‌ها اضافه می‌شوند و روابط فضایی آن‌ها با یال‌های بین گره‌های مربوطه نشان داده می‌شوند. به عنوان مثال، یک عکس هوایی را می توان به یک نمودار بدون جهت تبدیل کرد، جایی که رودخانه ها، ساختمان ها و جاده ها گره ها و لبه ها نشان دهنده روابط همسایگی آنها هستند.

مشارکت های این کار به شرح زیر است. اول از همه، ما یک رویکرد جدید برای جستجوی منطقه جغرافیایی متقاطع پیشنهاد می‌کنیم که مشکل را به عنوان یک کار تطبیق شباهت نمودار فرموله می‌کند. دوم، ما یک پایگاه داده گراف متقاطع چند منبعی ایجاد می کنیم که اولین معیار از این نوع در دسترس برای تحقیقات دیگر است. سوم، ما جستجوی کلاسیک مبتنی بر نقاط کلیدی را در مجموعه داده جدید خود ارزیابی می کنیم تا یک خط مبنا ایجاد کنیم. چهارم، ما رویکردی را برای یادگیری شباهت نمودار با استفاده از معماری سیامی‌مانند مبتنی بر شبکه عصبی گراف پیشنهاد می‌کنیم. آزمایش‌هایی که انجام دادیم نشان می‌دهد که روش پیشنهادی می‌تواند با موفقیت برای تطبیق داده‌های متقاطع استفاده شود و این یک راه امیدوارکننده است. هنوز هم برای کار چالش برانگیزتر بازیابی منابع متقابل چند ساله، بهبودهای زیادی وجود دارد.

ساختار باقی مانده این مقاله به شرح زیر است. ابتدا، ما تعریف مشکل و مفاهیم اساسی را که به پیشنهاد ما انگیزه می دهد در بخش ۲ ارائه می کنیم . ما پیشینه زمینه های تحقیقاتی مربوطه را در بخش ۷ ارائه می کنیم. این بخش مقاله پژوهشی را تکمیل می‌کند و مروری بر روش‌هایی که این کار بر آن‌ها استوار است ارائه می‌کند. با این حال، برای درک روش پیشنهادی لازم نیست. ما چارچوب پیشنهادی را ترسیم می‌کنیم که از یک شبکه کانولوشن گراف (GCN) به عنوان ستون فقرات و یک ساختار سیامی برای یادگیری جاسازی‌های نمودار در بخش ۳ استفاده می‌کند. ما یک مجموعه داده گراف بین‌زمان جدید را معرفی می‌کنیم که از عکس‌های تاریخی و شهودی که در پس تبدیل داده‌های بصری به داده‌های ساخت‌یافته است، بازیابی شده است.بخش ۴ . در بخش بعدی آزمایش های انجام شده برای ارزیابی رویکرد پیشنهادی را شرح می دهیم. بخش آخر، بخش ۸ ، کارهای آینده را تشریح می کند.

۲٫ بیان مشکل

در پروژه ما، هدف ما توسعه یک چارچوب یکپارچه برای تجزیه و تحلیل و نمایه سازی انواع مختلف منابع بصری، به دنبال نمایش مشترک بهینه ویژگی های مختلف از عکس های آرشیو، نقشه های تاریخی، نقشه های برداری مدرن و غیره است. این مقاله بر روی یک کار فرعی تمرکز دارد. در محدوده پروژه: تطابق مقطعی مناطق جغرافیایی بر اساس شباهت موجودات جغرافیایی که در آنها واقع شده است. این کار فرعی به ویژه دشوار است زیرا ممکن است چشم انداز در طول زمان تغییر کرده باشد. برای ارزیابی رویکرد خود، ما در این مقاله یک سناریوی مورد استفاده از تطابق متقاطع عکس‌های عمودی هوایی، بر اساس شباهت موجودیت‌های جغرافیایی که آنها نشان می‌دهند، ارائه می‌کنیم.

بازیابی تصویر هوایی به ویژه دشوار است، زیرا تقریباً همه تصاویر نشان دهنده یک نوع از موجودیت های جغرافیایی هستند: ساختمان ها، جاده ها، مسیرهای آب، مزارع، جنگل و غیره. در این وضوح، مشخصه اصلی که یک منطقه جغرافیایی را از سایرین متمایز می کند، توزیع فضایی است. از موجودیت های جغرافیایی موجود در آن. علاوه بر این، اکثر مناطق روستایی به هیچ وجه دارای اشیاء قابل تشخیص نیستند، زیرا توسط جنگل ها یا مزارع کشاورزی اشغال شده است. سه جهت نزدیک به مشکل در دست عبارتند از: تحقیقات متقاطع نقطه عطف بصری، تجزیه و تحلیل بازیابی اطلاعات بصری در مطالعات مختلف مبتنی بر تاریخی، و به طور کلی تر سنجش از دور (RS).

روش‌های گروه اول معمولاً مستلزم این هستند که اشیاء موجود در تصویر با وضوح بالاتر گرفته شوند و دارای نشانه‌های مشخصی باشند. سپس می‌توان ویژگی‌های آن‌ها را یاد گرفت که با استفاده از یک شبکه عصبی کانولوشنال (CNN) در بین نماها مطابقت داده شوند، همانطور که در [ ۷ ، ۸ ] انجام شد. با این حال، تصاویر هوایی آرشیو اغلب سطح قابل توجهی از جزئیات و وضوح بالایی ندارند و با استفاده از این روش ها نمی توان آنها را مطابقت داد. برخی از کارهای اخیر برای یادگیری رابطه بین ظاهر سطح زمین و ظاهر بالای سر و ویژگی های پوشش زمین از تصاویر سطح زمین دارای برچسب جغرافیایی کم موجود [ ۹ ، ۱۰ ، ۱۱ پیشنهاد شده است.]. روش‌ها پتانسیل خود را برای مشکل تعیین موقعیت جغرافیایی دنیای واقعی در منابع بصری نشان داده‌اند. با این حال، آنها به ویژه سناریوهای بین زمان را هدف قرار نمی دهند و در مکان های دیده نشده عملکرد ضعیفی دارند. تحقیقات بصری و بازیابی منطقه جغرافیایی در زمینه تصاویر هوایی با نمونه هایی از نرم افزارهای موجود مانند [ ۶ ] که در آن پایگاه داده های تصاویر هوایی به طور گسترده جستجو و تطبیق داده می شود تا یک قطعه از داده های زمینی در ایالات متحده را مکان یابی کند ، به میزان بسیار کمتری مورد تجزیه و تحلیل قرار گرفت. . گروه دوم روش‌ها از نظر مفهومی روش‌های متفاوتی را پوشش می‌دهند، اما همیشه فرض می‌شود که تصاویر حداقل تا حدی به صورت جغرافیایی ارجاع داده می‌شوند، همانطور که در تجزیه و تحلیل مبتنی بر فتوگرامتری عکاسی هوایی تاریخی [ ۱۲ ، ۱۳ ]]. تجزیه و تحلیل تغییرات معمولاً بر اساس پویایی مشخصه بصری است. به عنوان مثال، ر. [ ۱۲] کمیت کردن تغییرات حجمی در امتداد سواحل شنی از تصاویر آرشیوی با استفاده از تجزیه و تحلیل مبتنی بر فتوگرامتری. در این سناریو، تغییرات زمانی آنهایی هستند که باید با استفاده از داده های تاریخی ردیابی و تحلیل کمی یا کیفی شوند. سنجش از دور به لطف در دسترس بودن داده های دقیق مشاهدات زمین، اخیراً توجه بسیاری از محققان را به خود جلب کرده است. در حالی که رویکردها و کاربردها به طور قابل توجهی متفاوت است، ویژگی مشترک RS حجم زیاد، تنوع زیاد، سرعت زیاد، دقت زیاد و ارزش زیاد است که آگاهی را در مورد اهمیت پردازش تصویر در مقیاس بزرگ، ادغام، استخراج و نمایه سازی و بازیابی افزایش می دهد. . از این رو، نمایه سازی تصاویر نقش مهمی در حل مسائل RS ایفا می کند [ ۱۴ ، ۱۵ ]]. داده های تاریخی دارای چالش های پردازش مشابهی هستند و از مجموعه ای از ابزارهای نمایه سازی و بازیابی مناسب بهره مند خواهند شد.

شکل ۱ چارچوب یکپارچه را برای تحلیل منابع بصری چند بعدی چند بعدی ارائه شده در این کار نشان می دهد. همانطور که در این شکل نشان داده شده است، رویکرد جهانی ما با مرحله برداری از منابع بصری تاریخی آغاز می شود. این مرحله می تواند به صورت دستی یا با روش تقسیم بندی معنایی خودکار انجام شود. هدف آن استخراج موجودیت‌های اصلی جغرافیایی است که در منابع بصری نشان داده شده‌اند، ویژگی‌های آنها – مانند شکل، اندازه، جهت‌گیری، طبیعت و غیره و روابط فضایی آنها. با الهام از پیشرفت‌های اخیر رویکردهای مبتنی بر گراف یادگیری ماشین و دستاوردهای الگوریتم‌های تطبیق بصری مبتنی بر CNN، ما پیشنهاد می‌کنیم که از یک نمایش نمودار مشتق شده از این نتایج فرآیند تقسیم‌بندی معنایی برای مطابقت با تصاویر هوایی در طول زمان استفاده کنیم. به طور مشابه، برخی از روش های مبتنی بر بصری مانند [۹] بر یک تقسیم بندی قبلی تکیه می کنند که با استفاده از CNN در مرحله ای جداگانه ساخته می شود. تقسیم بندی معمولاً امکان تشخیص اشیاء مهم و قابل توجه موجود در یک تصویر را فراهم می کند. در حالی که CNN ها نتایج پیشرفته ای را در بخش بندی نشان می دهند، این مرحله همچنان مستعد خطا است. بنابراین این یک سوال باقی می ماند که آیا خطاهای احتمالی در این مرحله بر نتایج زیادی از کار تطبیق متقاطع زیر تأثیر می گذارد یا خیر. در این کار، ما وظیفه تقسیم‌بندی را برای تمرکز بر نمایش داده‌ها و مراحل تطبیق حذف می‌کنیم، از این رو استفاده از مجموعه داده‌های مشروح دستی را انتخاب می‌کنیم. این به ما امکان می دهد منبع بالقوه خطاها را به دلیل تقسیم بندی حذف کنیم و امکان سنجی بخش تطبیق الگوریتم را در تنظیم کنترل شده ارزیابی کنیم. بنابراین، در ادامه این مقاله بر روی مراحل ۱ تا ۴ رویکرد GisGCN تمرکز خواهیم کرد.

در مرحله ۱، نقاط مورد علاقه (POI) با استفاده از ویژگی های موجودات جغرافیایی موجود در منابع بصری تاریخی نمونه برداری می شوند. در مرحله ۲، موجودیت های جغرافیایی در ناحیه با اندازه از پیش تعریف شده در اطراف یک POI برای تشکیل گره های یک نمودار G استفاده می شوند. لبه ها بر اساس روابط فضایی بین موجودات جغرافیایی ساخته می شوند و گره ها با ویژگی های معنایی و هندسی موجودیت جغرافیایی مربوطه خود برچسب گذاری می شوند. با توجه به مجموعه نمودارها = با نشان دادن قلمرو اطراف یک POI در طول سالها، هدف ما بازیابی مناطق جغرافیایی تقریباً یکسان در طول زمان برای نمودار پرس و جو با استفاده از معیار تشابه است. بنابراین، مرحله ۳ با هدف یادگیری یک بردار جاسازی شده D از ساختار نمودار جغرافیایی است، که می تواند ویژگی های گره و روابط توپولوژیکی بین گره ها را در نظر بگیرد، در برابر نویز و تغییرات داده های حاصل از منابع مختلف یا تاریخ های مختلف مقاوم باشد، و جمع و جور باشد در مرحله ۴، این تعبیه‌ها برای جستجو و بازیابی سریع در پایگاه داده بزرگی از هزاران نمودار استفاده می‌شوند. شکل ۲طرح آموزش و ارزیابی مورد استفاده در مقاله ما را نشان می دهد. ما با استفاده از رویکرد یادگیری متضاد، روی مجموعه داده‌های مربوط به منطقه جغرافیایی شناخته شده آموزش می‌دهیم. در مرحله ارزیابی، شبکه از پیش آموزش دیده برای به دست آوردن یک توصیفگر از یک نمودار پرس و جو استفاده می شود، که سپس با استفاده از جستجوی K نزدیکترین همسایگان ( K NN) با پایگاه داده مطابقت داده می شود.

ما رویکرد پیشنهادی را GisGCN نامیدیم، جایی که Gis مخفف علم اطلاعات جغرافیایی است که در میان چیزهای دیگر، با نمایش و تجزیه و تحلیل اطلاعات جغرافیایی سروکار دارد، و GCN صرفاً اصطلاحی است که برای یک شبکه عصبی استفاده می‌شود که بر روی نمودارها کار می‌کند.

۳٫ GisGCN: یک مدل سیامی مبتنی بر GCN برای یادگیری جاسازی منطقه جغرافیایی

ما پیشنهاد می کنیم که اطلاعات توپولوژیکی رمزگذاری شده در ساختار گراف می تواند زمانی ضروری باشد که ما نیاز به تمایز بین دو منطقه جغرافیایی مختلف با مجموعه ای مشابه از اشیاء و ویژگی های هندسی مشابه داشته باشیم. بنابراین، ما یک خط لوله یادگیری جدید با استفاده از یک شبکه GCN [ ۱۶ ] برای یادگیری تطبیق مناطق جغرافیایی ارائه شده به عنوان نمودار در طول زمان پیشنهاد می‌کنیم. در کار اصلی، مدل GCN برای انجام یک کار طبقه‌بندی گره برای نمودارهای پراکنده بزرگ پیشنهاد شد. هدف مدل ما یادگیری یک فضای جاسازی برای نمودارهای جغرافیایی با اندازه متغیر با کاوش در مفهوم تطبیق نمودار عمیق است.

۳٫۱٫ ساختن نمودارها برای نشان دادن موجودیت های جغرافیایی و توزیع فضایی آنها

بنابراین برای هر منطقه جغرافیایی مورد علاقه، نموداری که پیکربندی فضایی آن را نشان می دهد، می تواند با معادله زیر خلاصه شود:

(۱)

جایی که:

منطقه مرجع است، یک اصطلاح عمومی که منطقه جغرافیایی مورد علاقه را در اطراف یک POI تعریف می کند،
X = مجموعه ای از مقادیر مرتبط با تمام گره ها، به اصطلاح ویژگی های گره،
l نوع موجودیت جغرافیایی است که هر گره به آن تعلق دارد،
ماتریس مجاورت برای رمزگذاری اطلاعات رابطه ای بین تمام گره ها است.

چنین نموداری را می توان از داده های برداری جغرافیایی که در مرحله پیش نیاز خط لوله پیشنهاد شده در شکل ۱ گرفته شده است، ساخته شود. POI را می توان با توجه به معیارهای کاربر، بر اساس ویژگی های موجودیت های جغرافیایی انتخاب کرد. اندازه مناطق جغرافیایی ساخته شده در اطراف POI ممکن است بسته به مقیاس تجزیه و تحلیل هر مورد استفاده متفاوت باشد. ویژگی‌های گره ویژگی‌هایی هستند که خصوصیات موجودیت‌های جغرافیایی را توصیف می‌کنند. آنها ممکن است توسط مجموعه داده بردار ورودی، در صورت وجود، ارائه شوند، یا از روی ویژگی های هندسی موجودیت های جغرافیایی با استفاده از روش های تحلیل فضایی کلاسیک [ ۱۷ ] محاسبه شوند. لبه ها از روابط فضایی بین موجودات جغرافیایی مشتق می شوند: آنها ممکن است روابط همسایگی ساده باشند که با استفاده از مثلث دلونی محاسبه شده اند [ ۱۸ ]] به عنوان مثال، یا روابط توپولوژیکی که در نمودار به عنوان لبه های برچسب گذاری شده پیاده سازی شده است.

۳٫۲٫ معماری مدل

دو نمودار داده شده است و ، جایی که A یک ماتریس اتصال و X پارامترهای گره است، ما مدلی می خواهیم که تابع یادگیری را تولید کند. از طریق GCN با پارامترهای قابل یادگیری w ، برای مقایسه آنها با امتیاز شباهت بین آنها در یک فضای برداری جدید. تابع رمزگذاری f مقادیر A و X یک POI فعلی و همه موجودیت های جغرافیایی در منطقه مرجع R را به عنوان ورودی می گیرد و اطلاعات زمینه مکانی جاسازی شده را خروجی می کند. مدل ما اجازه می دهد تا نمودارها را به توصیفگر تبدیل کنیم، که بازیابی کارآمد را با ساختارهای داده جستجوی سریع نزدیکترین همسایه امکان پذیر می کند.

در این کار، ما پیشنهاد می‌کنیم که شبکه‌های سیامی را برای مدیریت نمودارها برای یادگیری جاسازی‌های آنها تطبیق دهیم. در واقع، یک شبکه سیامی به ویژه در آموزش یک مدل با چند نمونه برای هر کلاس مؤثر است، که اغلب برای منابع تصویری تاریخی صادق است. شبکه سیامی از دو شبکه یکسان (با پارامترهای وزن قابل اشتراک گذاری) تشکیل شده است. در مورد ما، هر یک از شبکه ها اساساً یک GCN با maxpooling هستند، همانطور که در شکل ۳ نشان داده شده است. این مدل تعبیه تطبیق گراف از GNN [ ۱۶ ] الهام گرفته شده است و شامل چهار بخش اصلی است:

یک لایه کاملاً متصل برای تبدیل بردارهای ویژگی گره به یک فضای جدید،
یک لایه تجمع ویژگی مبتنی بر GCN با لایه‌های کاملاً متصل اضافی برای افزایش عمق،
یک لایه maxpooling،
یک لایه نهایی کاملا متصل

معماری به صورت شماتیک در شکل ۳ نشان داده شده است. لایه های تجمع از فرمول GCN توسط [ ۱۶ ] پیروی می کنند و به صورت زیر تعریف می شوند:

(۲)

که در آن A نرمال شده و اصلاح شده در [ ۱۶ ] ماتریس مجاورت است و W وزن هایی هستند که باید آموزش داده شوند و یک تابع فعال سازی ReLu است. همانطور که در کار اصلی توسط [ ۱۶ ] ما از دو لایه انتشار استفاده می کنیم، به طوری که نمایش برای هر گره اطلاعات را در محله محلی ۲-hop خود جمع می کند.

پس از اینکه نمایش گره های نهایی را به دست آوردیم، آنها را در سراسر آنها جمع می کنیم تا نمایش های سطح گراف را بدست آوریم. این توسط یک maxpooling ساده به دنبال یک عملیات MLP که نمایش گره را به یک بردار کاهش می دهد و سپس آن را تبدیل می کند، پیاده سازی می شود:

(۳)

که در آن X گره های گراف آموخته شده n ویژگی هستند.

معماری پیشنهادی عمدتاً با [ ۱۶ ] در نقطه (۳) تفاوت دارد که در آن ویژگی‌های سطح گره را محاسبه نمی‌کنیم، بلکه یک نمایش در سطح گراف را با انجام یک عملیات maxpooling بر روی گره‌ها در یک نمودار برای به دست آوردن کل نمودار محاسبه می‌کنیم. توصیف کننده ها مشابه [ ۱۹ ]. لایه ادغام گراف ورودی هر ساختار و اندازه را به یک خروجی با ساختار اندازه ثابت نگاشت می کند.

در طول آموزش، مدل جاسازی به طور مشترک در مورد ساختار نمودار و همچنین ویژگی‌های نمودار استدلال می‌کند تا به تعبیه‌ای برسد که منعکس کننده مفهوم شباهت توصیف شده توسط مثال‌های آموزشی باشد. مدل سیامی GCN پیشنهادی با از دست دادن کنتراست برای آموزش بر روی داده‌ها با مطابقت حقیقت زمینی وقف شده است. تابع زیان NT-Xent [ ۲۰ ] برای یک جفت مثال مثبت از تطبیق مناطق جغرافیایی در طول زمان ( i , j ) به صورت زیر تعریف می شود:

(۴)

جایی که: دما است، سیم( ، ) – تشابه کسینوس، i ، j – دو نمودار در دسته ای با اندازه N. ضرر نهایی به عنوان میانگین حسابی در تمام جفت‌های مثبت، هر دو ( i ، j ) و ( j ، i )، در یک دسته کوچک محاسبه می‌شود.

(۵)

به دنبال ایده [ ۲۰ ]، پیشنهاد می کنیم دسته هایی از نمودارهای تصادفی برای آموزش مدل ایجاد کنیم. با این حال، به‌جای تغییر آن‌ها برای استفاده به عنوان ورودی برای شاخه دوم GCN سیامی، نمودارها را نشان‌دهنده همان منطقه جغرافیایی اما از یک چارچوب زمانی متفاوت برای تشکیل نمونه‌های مثبت می‌گیریم. سپس از دست دادن تعبیه‌ها را برای همان منطقه جغرافیایی تشویق می‌کند تا در فضای جاسازی از نظر فاصله کسینوس نزدیک‌تر باشند. و تعبیه مناطق مختلف از هم دورتر باشد.

۳٫۳٫ بازیابی بر اساس شباهت مناطق جغرافیایی

هنگامی که مدل آموزش داده شد، می‌توان از آن برای ایجاد جاسازی‌های بیشتر نمودار برای مناطقی با مکان ناشناخته استفاده کرد که یک نمایش بصری تاریخی در تاریخ معینی برای آن‌ها وجود دارد. سپس تعبیه‌های به‌دست‌آمده را می‌توان با مواردی که در طول آموزش مدل با استفاده از معیارهای پیشرفته مانند شباهت کسینوس یا فاصله L2 از قبل محاسبه شده است، مقایسه کرد. اگر ناحیه جستجو شده در پایگاه داده آموزشی ما نشان داده شود، پس جاسازی آن باید امتیاز تشابه بالاتری با نمودارهایی که همان ناحیه را در تاریخ های مختلف نشان می دهند به دست آورد، بنابراین مکان ناحیه جستجو شده را امکان پذیر می کند. در حالت ایده‌آل، باید امتیاز بالاتری را با نزدیک‌ترین تعبیه زمانی به‌دست آورد، مشروط بر اینکه بازنمایی‌های تاریخی موجود دارای همان سطح جزئیات باشند.

۴٫ آماده سازی مجموعه داده

مورد استفاده هدف ما به عکس‌های هوایی باستانی می‌پردازد که تکامل چشم‌انداز فرانسه را در طول زمان به تصویر می‌کشد: بنابراین ما برای هر مجموعه عکس‌هایی که همان منطقه را در تاریخ‌های مختلف نشان می‌دهند، به حاشیه‌نویسی نیاز داریم. علاوه بر این، بازیابی تصویر هوایی بسیار دشوار است، زیرا تقریباً همه تصاویر نشان دهنده یک نوع از موجودیت های جغرافیایی هستند: ساختمان ها، جاده ها، آبراهه ها، مزارع، جنگل و غیره. در این وضوح، ویژگی اصلی که یک منطقه جغرافیایی را از سایرین متمایز می کند، توزیع فضایی موجودات جغرافیایی موجود در آن. بنابراین برای به حداکثر رساندن شانس خود، بر مناطق جغرافیایی که نقاط دیدنی در آن قرار دارند تمرکز می کنیم.

۴٫۱٫ انتخاب داده های ورودی

مجموعه داده ورودی در آزمایش‌های ما از عکس‌های فوری زمانی یک پایگاه داده برداری توپوگرافی ساخته شده است که دقیقاً با تصاویر هوایی عمودی گرفته شده از سه بخش فرانسوی مطابقت دارد (به اصطلاح “بخش‌ها” بخش‌های اداری قلمرو فرانسه هستند): Moselle, Bas-Rhin. و Meurthe-et-Moselle در چهار سال مختلف (۲۰۰۴، ۲۰۱۰، ۲۰۱۴ و ۲۰۱۹). داده های مورد استفاده برای ایجاد مجموعه داده ما از آژانس نقشه برداری فرانسه (IGN) [ ۲۱ ] سرچشمه می گیرد. آنها به صورت دستی، با پیروی از قوانین جمع آوری داده ها و به روشی افزایشی در طول زمان، حاشیه نویسی شده اند. بنابراین آنها بسیار همگن هستند و به ویژه از نظر هندسی در طول زمان بسیار سازگار هستند ( شکل ۴ را ببینید). ما انواع موجودات جغرافیایی زیر را برای برجستگی بصری آنها در چشم انداز و دوام آنها انتخاب کرده ایم: جاده ها، راه آهن، آبراه ها، ساختمان ها، فرودگاه ها، امکانات ورزشی، و گورستان ها. برای هر بخش و هر عکس فوری زمانی، ما از نمایش‌های هندسی موجودیت‌های جغرافیایی و همچنین اطلاعات ویژگی‌های مرتبط با آنها برای ایجاد نموداری استفاده می‌کنیم که توزیع فضایی کلی آنها را در قلمرو توصیف می‌کند.

برای آزمایش پتانسیل تعمیم روش ما، به ناهمگونی بیشتری بین هندسه ها نیاز داریم، گویی که توسط برخی از الگوریتم های تقسیم بندی خودکار تولید شده اند. بنابراین، ما همچنین داده‌هایی را برای انواع موجودیت‌های جغرافیایی، که از نقشه خیابان باز [ ۲۲ ] (OSM) برای دو بخش (Moselle و Meurthe-et-Moselle) گرفته شده بود، اضافه کردیم. داده‌های OSM توسط جمع‌سپاری، بدون قوانین جمع‌آوری داده‌های دقیق تولید می‌شوند، و بنابراین، به احتمال زیاد هندسه‌های ناهمگن دارند. آنها فقط در جدیدترین نسخه مورخ ۲۰۲۰ در دسترس هستند. علاوه بر این داده‌های متقاطع، ما همچنین نویز تولید شده به‌طور تصادفی را که به ویژگی‌های هندسی در مجموعه داده تک منبع اضافه می‌شود، آزمایش می‌کنیم.

۴٫۲٫ تعریف مناطق جغرافیایی مورد علاقه

برای اطمینان از اینکه نواحی نشان‌داده‌شده توسط نمودارهای ما دارای موجودیت‌های جغرافیایی کافی برای شناسایی آن‌ها هستند، نمودارهای خود را پیرامون POI می‌سازیم: ساختمان‌های مذهبی، اشیاء و بناهای تاریخی، قلعه‌ها یا قلعه‌ها، ساختمان‌های دولتی محلی، ساختمان‌های دارای عملکرد ورزشی، ایستگاه‌های راه‌آهن. ، فرودگاه ها و غیره. ما مراکز هندسی دقیق POI را انتخاب می کنیم و به طور تصادفی یک جابجایی کوچک به مختصات شرقی و شمالی آن تا ۱۰ متر اضافه می کنیم. نمونه ای از مناطق جغرافیایی انتخاب شده برای پایگاه داده در شکل ۵ نشان داده شده است ، جایی که کادرهای محدود کننده ابعاد m بر روی تصاویر فیلم هوایی قرار گرفته اند.

برای هر نسخه پایگاه داده برداری (یعنی ۲۰۰۴، ۲۰۱۰، ۲۰۱۴ یا ۲۰۱۹)، به طور تصادفی مرکز کادرهای مرزی را تا ۲۰% تغییر می دهیم تا ناحیه نمایش داده شده برای یک سناریوی بازیابی واقعی تر، یکسان نباشد. برخی از POI های انتخاب شده به طور اتفاقی نزدیک به یکدیگر بودند، بنابراین جعبه های محدود کننده اطراف آنها همپوشانی دارند. اگر سطح همپوشانی بیش از ۵۰% باشد، نمودارهای حاصل را نمایانگر همان منطقه جغرافیایی در نظر می گیریم و به این منطقه همان شناسه منحصر به فرد را اختصاص می دهیم. این منجر به تعداد کمی از مناطق می شود که مطابقت های غیر منحصر به فردی در پایگاه داده دارند (برای جزئیات به جدول ۱ مراجعه کنید). ما برچسب ها را پس از ایجاد نمودار با استفاده از الگوریتم Union Find [ ۲۳ ] دوباره اختصاص می دهیم. نمونه ای از ناحیه غیر منحصر به فرد در شکل ۵ نشان داده شده است: دو کادر کراندار پایین سمت چپ روی هم را ببینید.

برای هر یک از این مناطق مورد علاقه، اطلاعات معنایی موجود در داده های برداری توپوگرافی و هندسه آنها برای ایجاد یک نمودار رابطه ای استفاده می شود. با ویژگی های X ، همانطور که در زیر توضیح داده شده است.

۴٫۳٫ ساختن نمودار

برای هر POI e ، نموداری می سازیم که بافت جغرافیایی آن را توصیف می کند یعنی موجودات جغرافیایی واقع در ناحیه جغرافیایی اطراف آن و روابط فضایی آنها.

۴٫۳٫۱٫ ایجاد گره ها و لبه ها

هر گره V گراف نشان دهنده یک موجودیت جغرافیایی واحد است. در آزمایش‌های خود، انواع موجودیت‌های جغرافیایی زیر را به‌عنوان گره‌ها برای نمودار انتخاب می‌کنیم: ساختمان‌ها، بخش‌های توپولوژیک جاده‌ها، بخش‌های توپولوژیک مسیرهای آب، بخش‌های توپولوژیکی راه‌آهن، فرودگاه‌ها، امکانات ورزشی، گورستان‌ها. ما آنها را انتخاب می کنیم زیرا آنها کاملاً دائمی هستند، به وضوح قابل مشاهده هستند و از نظر ساختاری نشانه های مهم در تصاویر هوایی عمودی هستند.

مختصات جغرافیایی گره ها را به عنوان یک مجموعه مسطح محدود در نظر می گیریم تا رابطه همسایگی بین آنها را محاسبه کرده و لبه های نمودار را بسازیم. توسن و همکاران [ ۲۴ ] سه روش را برای اتصال و خوشه بندی مجموعه ای از نقاط مقایسه کرد. بر اساس تجزیه و تحلیل آنها، ما مثلث سازی Delaunay [ ۱۸ ] را بین مرکز هندسه گره ها انتخاب کردیم، زیرا این روش بیشترین مقدار یال ها را بین نقاط همسایه محلی فراهم می کند. ما همچنین با Range Neighboring Graphs (RNG) آزمایش کردیم و کد ایجاد نمودار RNG را همراه با یکی از Delaunay ارائه کردیم. هر دو روش برای تضمین تشکیل نمودارهای متصل انتخاب شده اند.

۴٫۳٫۲٫ افزودن برچسب های معنایی به گره ها

گره های نمودار دارای برچسب های مجزا هستند که نشان دهنده ماهیت آنهاست: رودخانه، جاده، راه آهن، ساختمان های مذهبی، قلعه، قلعه، برج، قوس، بنای یادبود، گورستان، زمین ورزشی، ساختمان معمولی، ساختمان های عمومی و فرودگاه. در مواردی که برخی از برچسب های دقیق در دسترس نباشد، که گاهی اوقات برای ساختمان ها وجود دارد، برچسب “ساختمان عادی” اعمال می شود.

۴٫۳٫۳٫ افزودن ویژگی های هندسی به گره ها و لبه ها

هر گره همچنین دارای ویژگی های هندسی X (محیط عادی شده و خروج از مرکز) است. بسیاری از ویژگی‌های هندسی دیگر معمولاً در تحلیل فضایی استفاده می‌شوند، مانند جهت‌گیری کلی، محورهای میانگین اشکال هندسی، توصیف‌گرهای سطح و توصیف‌کننده‌های شکل‌های مختلف [ ۱۷ ]. با این حال، ما این تحقیق را به ساده‌ترین مواردی که برای جبران سطوح مختلف جزئیات در حاشیه‌نویسی‌ها در طول زمان و منابع داده و اجتناب از ایجاد فرضیات در جهت‌گیری صحنه، به هیچ اطلاعات جهت‌گیری یا جزئیات بالایی نیاز ندارند، محدود کردیم. عجیب و غریب در مورد ما به سادگی است ، که در آن L و W طول و عرض جعبه مرزی حداقل هندسه است. محیط عادی به سادگی است .

ما همچنین ویژگی های لبه را به شکل فاصله نرمال شده بین گره ها ذخیره می کنیم. گزینه دیگر استفاده از زوایا است، اما این ویژگی این ویژگی را وابسته به جهت می‌کند و ما به دنبال چرخش و تغییر مقیاس بودن نمودارها هستیم: از این رو، زوایای بین اشیا را نمی‌توان به عنوان وزن لبه در سناریوی ما استفاده کرد. توجه داشته باشید که ما بعداً در آزمایش‌های خود از لبه‌ها استفاده نمی‌کنیم، بلکه آنها را برای تحقیقات آینده می‌گذاریم، و این کار را به چالش‌برانگیزترین سناریوی موردی محدود می‌کنیم. بنابراین نمودارهای موجود در مجموعه داده ما بدون جهت و بدون وزن هستند.

کد طراحی‌شده برای ایجاد نمودار از داده‌های شکل فایل برداری در یک مخزن باز موجود در اینجا موجود است: https://www.alegoria-project.fr/en/GENR_dataset (در ۲۸ اکتبر ۲۰۲۱ قابل دسترسی است).

۴٫۴٫ بحث در مورد مجموعه داده نمودارهای حاصل

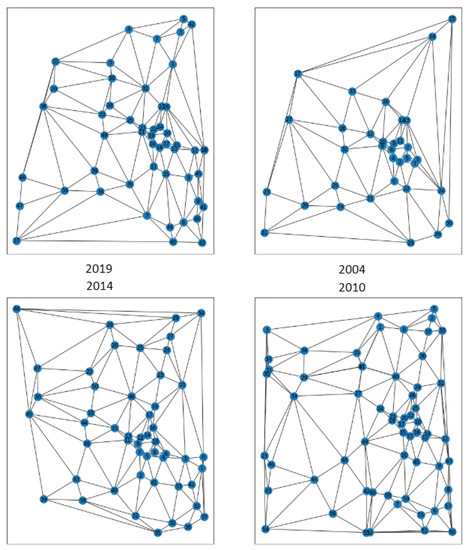
نمونه ای از نمودارهای به دست آمده نشان دهنده همان منطقه در طول زمان در شکل ۶ نشان داده شده است . به تفاوت چشم انداز و ساختار نمودار مربوطه در دو تاریخ متناظر با فاصله ۱۵ ساله توجه کنید. مشاهده می کنیم که در برخی موارد تغییرات بسیار قابل توجه است. حتی زمانی که فاصله زمانی کم است، این مورد برای نمودارهای متقاطع نیز صادق است. دو نمونه از نمودارهای متقاطع حاصل در شکل ۷ و شکل ۸ نشان داده شده است. از نظر بصری، بیشترین تغییرات در دسته‌بندی اشیا مانند جاده‌ها و جوی‌های آب است و تغییرات کمتری در ساختمان‌ها دیده می‌شود، اگرچه گره‌هایی از دسته «ساختمان» وجود دارد که در طول زمان ظاهر و ناپدید می‌شوند.

جدای از استفاده از مناطق جغرافیایی منطبق از سه بخش ذکر شده در بالا، ما همچنین برخی از داده های درهم و برهم را بدون مکاتبات از بخش چهارم فرانسوی، یعنی Côtes-d’Armor اضافه می کنیم تا سناریوی نمایه سازی و بازیابی برای داده های منبع مشابه را چالش برانگیزتر کنیم. جدول ۱ داده های موجود در پایگاه داده نموداری را که برای بازیابی منطقه جغرافیایی در طول زمان ایجاد کرده ایم، ارائه می دهد. توجه داشته باشید که حداکثر تعداد گره ها در یک گراف منفرد ۱۵۰ است. این به عمد انجام می شود، ما فقط چندین منطقه جغرافیایی را با تعداد رئوس بیشتر حذف کردیم تا اندازه نمودار نهایی محدود شود. به طور مشابه، ما تمام نمودارهایی را با کمتر از ۳ گره حذف کردیم. این انتخاب با انتخاب مدل GCN در ادامه این کار توضیح داده شده است.

۴٫۵٫ نمودار آمار مجموعه داده ها

نمونه ای از مشخصات و توزیع داده های نمودار نهایی برای بخش موزل در جدول ۲ خلاصه شده است. دیدن تفاوت بین توزیع داده ها در طول سال ها جالب است. همچنین توجه داشته باشید که تغییر خاصی در تعداد گره‌ها و یال‌ها در سال ۲۰۱۴ وجود دارد – این احتمالاً به دلیل تغییراتی در فرآیند جمع‌آوری دستی داده‌های برداری است زیرا ما از همان کد برای تبدیل داده‌های برداری به نمایش نمودار برای همه سال‌ها استفاده می‌کنیم. هر دو منبع به نظر می‌رسد توزیع مشخصه نمودار برای پایگاه‌های داده مختلف با شکاف کوچک، تقریباً مشابه است، با گره‌های کمتری برای نمودارهای OSM نسبت به نمودارهای IGN، که همراه با مشاهدات ما است که داده‌های IGN سطح جزئیات بالاتری در گستره جغرافیایی مجموعه داده ما دارند. .

همانطور که در بالا توضیح داده شد، مجموعه داده ما همیشه شامل مناطق جغرافیایی یکسان در هر سال نیست، به عنوان مثال، جعبه های مرزی برای یک سناریوی واقعی تر جابجا می شوند. بنابراین ما تجزیه و تحلیل آماری شباهت ویژگی‌ها را بین داده‌های نمودار تطبیق ارائه می‌کنیم. برای این منظور، تقاطع بیش از اتحادیه (IOU) بین دو نمودار که منطقه جغرافیایی یکسانی را در طول زمان نشان می‌دهند استفاده می‌شود:

(۶)

جایی که ویژگی های هندسی گره ها هستند که موجودیت های جغرافیایی را نشان می دهند . توزیع های حاصل از IOU بین نمودارهای منطبق که از منبع داده یکسانی می آیند در شکل ۹ نشان داده شده است. با این حال، توزیع های به دست آمده همیشه نرمال نیستند. با تجزیه و تحلیل هیستوگرام‌های به‌دست‌آمده، می‌توانیم ببینیم که تعداد گراف‌هایی که مقادیر IOU کوچک‌تر دارند، زمانی که اختلاف زمان بزرگ‌تر باشد، بیشتر است. از آنجایی که چشم انداز و در نتیجه موجودات جغرافیایی موجود در آن به احتمال زیاد در یک دوره زمانی طولانی تکامل یافته اند تا در یک بازه زمانی کوتاه، منطقی به نظر می رسد که تفاوت بین نمودارهای زمان های معتبر بسیار متفاوت بیشتر از تفاوت بین نمودارهای نزدیک به زمان باشد. .

شکل ۱۰ تجزیه و تحلیل آماری منبع متقاطع را برای IOU بر روی ویژگی های گره نشان می دهد. هنگام محاسبه IOU برای نمودارهای متقاطع، یک پارامتر جدید d را معرفی کردیم که مربوط به تعداد ارقام بعد از نقطه اعشار در مقادیر مشخصه پیوسته است. ما مشاهده کردیم که با تغییر مقدار d ، هیستوگرام های نسبتاً متفاوتی از IOU بدست می آوریم، همانطور که در شکل ۱۱ a نشان داده شده است. با استفاده از هیستوگرام ها و بر اساس نتایج تجربی بخش بعدی، d را انتخاب می کنیم= ۳ برای آزمایش داده های متقابل منبع. علاوه بر این، با یک بررسی بصری و تجزیه و تحلیل هیستوگرام بیشتر، متوجه شدیم که ساختمان‌ها پایدارترین ویژگی‌های هندسی را در بین دو پایگاه داده و رودخانه‌ها کمترین دارند. این احتمالاً به دلیل این واقعیت است که از همان طرح کاداستر برای حاشیه نویسی ساختمان ها برای منابع داده OSM و IGN استفاده شده است. هیستوگرام در شکل ۱۱ ب، IOU را برای ویژگی های دسته های مختلف خلاصه می کند. با این حال، در طول زمان، میانگین امتیاز IOU برای داده های متقاطع بسیار کمتر از همان منبع باقی می ماند.

بنابراین ما یک مجموعه داده متقاطع با منبع متقاطع ایجاد کرده‌ایم که شامل نمایش نمودارهای مناطق جغرافیایی منطبق است. برای تعمیم‌پذیری، داده‌ها از دو منبع مختلف گرفته شده‌اند: نقشه خیابان باز [ ۲۲ ] (OSM) و آژانس نقشه‌برداری فرانسه (IGN) [ ۲۱ ]]. انتخاب این تاریخ‌های خاص برای آزمایش‌های ما بر اساس در دسترس بودن عکس‌های هوایی و داده‌های برداری مربوط به آن‌ها تعیین شد. ما از نظر آماری این فرض را تأیید کردیم که هر چه شکاف زمانی بزرگتر باشد، نمودارهای حاصل برای همان منطقه متفاوت تر هستند. ما تا حد امکان از تاریخ‌های متوسط استفاده کردیم تا ارزیابی کنیم که چگونه دقت رویکردمان به تعداد تغییرات چشم‌انداز ساخته‌شده توسط انسان در طول سال‌ها بستگی دارد. سپس این نمودارهای متقابل پایگاه داده متقاطع نهایی که مناطق جغرافیایی تقریباً یکسانی را نشان می‌دهند برای ارزیابی عملکرد روش GisGCN پیشنهادی استفاده می‌شوند. به طور کلی، ما انتظار داریم که رویکرد ما برای مواردی کار کند که تعداد قابل توجهی از اشیاء در منطقه جغرافیایی معین در طول سال‌ها حفظ شده باشند، و ما آگاه هستیم که با افزایش بازه زمانی عملکرد می‌تواند کاهش یابد.

۵٫ آزمایش ها و ارزیابی مدل

در این بخش، ما دو روش برای مقایسه داده های تولید شده از نسخه های مختلف BD TOPO ارائه می کنیم. پایگاه داده برای یافتن کسانی که همان منطقه از قلمرو جغرافیایی را نشان می دهند. اولین مورد، بدون نظارت، به سادگی مقادیر مشخصه محاسبه شده را همانطور که در بخش ۳ ارائه شده است، مقایسه می کند . دومی از جاسازی‌های نموداری استفاده می‌کند که با استفاده از شبکه ارائه‌شده در بخش قبل تولید شده‌اند.

۵٫۱٫ جستجوی شباهت بدون نظارت بر اساس ویژگی ها

ما از یک خط پایه بدون نظارت برای تعیین اینکه آیا ویژگی های هندسی اشیاء صحنه به تنهایی برای کار تطبیق گراف کافی است، بدون استفاده از هیچ گونه اطلاعات توپولوژیکی (یعنی نمایش نمودار) و هر گونه یادگیری، استفاده می کنیم. ما از K Nearest Neighbors ( K NN) برای بازیابی ۵ نتیجه تطبیق برتر و گزارش مقدار دقت متوسط نقشه ( map@5 ) استفاده می کنیم:

(۷)

که در آن N تعداد پرس و جوها است، دقت متوسط برای یک پرس و جو، K = ۵ است.

ما از کتابخانه فیس بوک AI Similarity Search (Faiss) [ ۲۵ ] برای بازیابی مناطق جغرافیایی در طول زمان استفاده می کنیم. Faiss برای جستجوی اسناد چندرسانه ای مشابه با یکدیگر با استفاده از الگوریتم K NN طراحی شده است. ما استفاده می کنیم اندازه گیری فاصله برای بازیابی مشابه ترین مناطق جغرافیایی در طول سال ها بر اساس ویژگی های هندسی محلی و معنایی هر شی موجود در صحنه. سایر معیارهای تشابه موجود در Faiss از نظر تجربی کارآمدی کمتری داشتند.

نتایج جستجوی شباهت مبتنی بر فایس در جدول ۳ خلاصه شده است. نقشه بدست آمده @۵نمرات بسیار بالا هستند، به این معنی که ویژگی های معنایی و هندسی به اندازه کافی نماینده برای توصیف مناطق جغرافیایی هستند. با این وجود، هنوز فضایی برای بهبود وجود دارد که به طور بالقوه می توان با استفاده از اطلاعات توپولوژیکی بین گره ها، یعنی نمایش گراف، به دست آورد. جالب است که ببینید وقتی داده های برگشتی واقعا اشتباه هستند. توجه داشته باشید که حتی اگر منطقه جغرافیایی مکاتبات واقعی از سال ۲۰۰۴ شامل بسیاری از نهادهای موجود در سال ۲۰۱۹ باشد، مناطق دیگر به جای آن بازگردانده شدند. این مثال محدودیت جستجوی فقط ویژگی ها را نشان می دهد، زمانی که هیچ اطلاعات رابطه ای در مورد صحنه استفاده نمی شود. در همان لحظه، می‌توانیم ببینیم که تغییرات قابل توجهی در ساختار نمودار در طول سال‌ها وجود دارد، که در حالت ایده‌آل می‌خواهیم در سناریوی تطبیق گراف قوی باشیم.شکل ۱۲ .

به طور کلی، همه نتایج ما نشان می دهد که هرچه فاصله زمانی بین پرس و جو و پایگاه داده کمتر باشد، نتایج بازیابی map@5 بهتر است. این منطقی به نظر می رسد زیرا اختلاف چارچوب زمانی باید به تعداد تغییرات چشم انداز رخ داده مرتبط باشد. یک افت ناگهانی در دقت بازیابی بین داده های متقاطع با فاصله ۱۰ ساله وجود دارد.

۵٫۲٫ گره استحکام را در حضور نویز مشخص می کند

در پایگاه داده ما به اصطلاح منبع ، ویژگی‌های گره بسیار دقیقی با دقت شش اعشار داریم که به لطف دسترسی به داده‌های برداری دستی و افزایشی مشابه هستند. مخصوصاً برای آزمایش‌هایی که داده‌ها از یک منبع می‌آیند، و نتایج مربوط به map@5 بالاتر از cross-source map@5 است.اگر همان اطلاعات باید به طور خودکار از تصاویر استخراج می شد، شباهت ویژگی گره به دلیل خطاهای موجود در مراحل تقسیم بندی و برداری کاهش می یافت. برای شبیه‌سازی این سناریوی واقعی، گروهی از آزمایش‌ها را با کاهش تعداد اعشار در ویژگی‌های گره تا یک، دو و سه اعشار و با اضافه کردن نویز توزیع شده معمولی با = ۰ و = [۰٫۱، ۰٫۰۱، ۰٫۰۰۱] به ویژگی های پرس و جو. نتایج روش فایس با نویز گاوسی اضافه شده و ویژگی‌های پرس‌وجو با دقت کمتر در جدول ۴ خلاصه شده‌اند .

۵٫۳٫ مدل GisGCN

ما دو سناریو زیر را در جدول ۵ برای مشکل یادگیری شباهت نمودار در نظر می گیریم:

سناریو اول با هدف یادگیری جاسازی‌ها با استفاده از جفت نمودارها از مجموعه داده‌های ما، و اطلاعات زمانی برای تقسیم داده‌ها به زیر مجموعه‌های آموزشی، اعتبارسنجی و آزمایش استفاده می‌شود. دقیقاً، ما در ۲۰۱۹-۲۰۱۰ تمرین می کنیم، در ۲۰۱۹-۲۰۱۴ اعتبارسنجی می کنیم و در نهایت جفت های ۲۰۱۹-۲۰۰۴ و ۲۰۱۰-۲۰۰۴ مجموعه آزمایشی را تشکیل می دهند.
در سناریوی دوم، مجموعه داده‌ها را نه تنها بر اساس سال، بلکه بر اساس بخش‌ها نیز تقسیم می‌کنیم تا تعمیم‌پذیری روش خود را ارزیابی کنیم. به عنوان مثال، ما از جفت های ۲۰۱۹-۲۰۰۴ از بخش Moselle برای آموزش و از جفت های ۲۰۱۹-۲۰۰۴ از Meurthe-and-Moselle برای آزمایش استفاده می کنیم.

هر دو سناریو برای داده های منبع و منبع متقابل یکسان مستقر شده اند . علاوه بر این، ما سعی می کنیم مدل یاد گرفته شده را مستقیماً به منبع داده جدید منتقل کنیم تا عملکرد آن را در این منبع داده بیشتر ایجاد کنیم. ما شباهت بین توصیفگرهای نهایی را با استفاده از یک متریک شباهت L2 ساده در فضای برداری از کتابخانه Faiss محاسبه می کنیم و نتایج را با استفاده از متریک map@K ارزیابی می کنیم. توجه داشته باشید که شباهت در تابع ضرری که استفاده می کنیم، شباهت کسینوس است. با این حال، ما دریافتیم که فاصله L2 در زمان استنتاج بهتر کار می کند. ما همچنین میانگین زمان بازیابی را برای یک پرس و جو گزارش می کنیم.

۵٫۴٫ پارامترهای مدل

در طول آزمایش‌ها، ابعاد تعبیه‌های گراف را روی ۵۱۲ ثابت کردیم، و مقادیر رایج زیر را امتحان کردیم: ۱۲۸، ۲۵۶، ۵۱۲٫ آزمایش‌های ما بر روی داده‌های “منبع یکسان” نشان داده است که وقتی اندازه توصیفگر نهایی کمتر از ۵۱۲ باشد، یادگیری ظرفیت های مدل ثابت می ماند، اما ظرفیت های تعمیم برای تطبیق زمان متقابل در فریم های زمانی جدید بسیار کمتر است. ما می توانیم همان مقادیر map@5 را در مجموعه آموزشی با تمام اندازه های توصیفگر به دست آوریم. با این حال، اعتبارسنجی map@5 به فلات می‌رسد و افزایش برای map@5 پایین‌تر متوقف می‌شودمقادیر در مورد اندازه توصیفگر کوچکتر. ما مشاهده کردیم که تابع ضرر از روند مشابهی پیروی می کند و هر چه اندازه توصیفگر کوچکتر باشد، مدل سریعتر شروع به برازش داده های آموزشی می کند. اولین لایه FC دارای اندازه ثابت است و ویژگی ها را به فضای ۱۲۸ بعدی ترسیم می کند.

ما از دو لایه GCN اصلاح شده در ستون فقرات مدل خود استفاده می کنیم. وزن‌ها در لایه‌های GCN نیز برابر با ۵۱۲ است، اگرچه ما با پارامترهای مختلف از ۱۲۸ تا ۱۰۲۴ آزمایش کردیم. مشاهده کردیم که تعداد کمتر وزن‌ها منجر به عدم تناسب داده‌های ما می‌شود. ابعاد لایه FC اضافه شده به لایه های GCN نیز برابر با ۵۱۲ است.

۵٫۵٫ پارامترهای آموزشی

در مرحله پیش پردازش گراف، برچسب‌های گسسته گره‌ها به صورت یک داغ کدگذاری شدند و ویژگی‌های پیوسته دست نخورده باقی ماندند و با ویژگی‌های کدگذاری‌شده یک‌گرم الحاق شدند. از آنجایی که گراف ها تعداد گره های متفاوتی دارند، از padding برای ایجاد نمودارهایی با اندازه ورودی به شبکه استفاده می کنیم. بنابراین حداکثر تعداد گره‌ها در یک نمودار منفرد روی ۱۵۰ تنظیم شد. نمونه‌ای از نمودارها برای همان منطقه در طول سال‌ها در شکل ۱۳ نشان داده شده است . اولین لایه کاملا متصل با وزن های یادگیری مدل، ویژگی ها را در ۱۲۸ بعد ترسیم می کند.

جفت‌های گراف آموزشی در طول زمان اجرا انتخاب می‌شوند و در پایان هر دوره به‌طور تصادفی با هم مخلوط می‌شوند. این شبکه برای تقریباً ۲۰۰ دوره آموزش داده می شود تا زمانی که دقت نقشه اعتبارسنجی @۵ به فلات برسد و شروع به کاهش کند. در مورد آموزش یک بخش، ۱۰۰ دوره برای غنی سازی حداکثر دقت اعتبار کافی بود. آموزش بیشتر منجر به تطبیق بیش از حد با مجموعه آموزشی می شود، بنابراین مدلی را انتخاب می کنیم که بهترین امتیاز اعتبار سنجی را نشان می دهد و نتایج آن را گزارش می کنیم. ما در تمام آزمایش‌ها از اندازه دسته ۶۴ نمودار استفاده کردیم.

ما از هیچ تکنیک افزایش داده استفاده نمی کنیم و از دست دادن NT-Xent اجازه می دهد تا از استخراج نمونه سخت که معمولاً برای آموزش شبکه سیامی استفاده می شود جلوگیری شود. پارامتر دما در افت کنتراست برابر است با . بهینه ساز Adam [ ۲۶ ] برای بهینه سازی وزن های یادگیری انتخاب شده است. میزان یادگیری برابر است با ، با پوسیدگی و یک زمان‌بندی نرخ یادگیری چند مرحله‌ای، که پس از ۸۰ و ۱۲۰ دوره با گاما ۰٫۰۵ کاهش می‌یابد. تمام آموزش ها بر روی یک CPU انجام می شود و به قدرت محاسباتی بیش از حد نیاز ندارد، عمدتا به دلیل اندازه کوچک نمودارهای ما. حدود ۱۲ ساعت طول می کشد تا مدل را به صورت انتها به انتها در مجموعه داده ما با ۵۷۳۲ نمودار در دو سال مجزا از پایگاه داده آموزش دهیم، همراه با محاسبه دقت map@5 برای آموزش و داده های اعتبار سنجی پس از هر دوره. یک شاخه واحد از مدل سیامی در مرحله استنتاج استفاده می شود.

۶٫ بحث

جدول ۶ نتایج مربوط به سناریوی یادگیری متقاطع را برای توصیفگرهای مبتنی بر GCN ما خلاصه می کند. ما عملکرد توصیفگرهای سراسری و محلی را گزارش می‌کنیم و تعبیه‌های گره حاصل را قبل از لایه maxpooling می‌گیریم. ما مشاهده کردیم که محاسبه دومی بسیار بیشتر طول می کشد و عملکرد کمتری نسبت به موارد جهانی دارد که با هدف یادگیری ما مطابقت دارد. به طور متوسط، زمان بازیابی برای پرسشی که به عنوان یک توصیفگر منفرد نشان داده می شود، دو برابر کمتر از زمانی است که با ویژگی های محلی Faiss قبلاً در همان رایانه به دست آمده بود. مقادیر map@5 به‌دست‌آمده کمتر از مقادیر به‌دست‌آمده با جستجوی شباهت کاملاً مبتنی بر ویژگی از خط پایه ما است.

در مرحله بعد، ارزیابی کردیم که آیا می‌توان از همان شبکه آموزش‌دیده منبع برای سناریوی بازیابی منبع متقاطع با پرس‌وجو از داده‌های OSM با مدل از پیش آموزش داده شده IGN استفاده کرد یا خیر. مقادیر map@5 به‌دست‌آمده بسیار کم هستند، اگرچه با نتایج پایه در مورد فاصله زمانی بزرگ بین دو منبع مطابقت دارند. بنابراین، می‌توان نتیجه گرفت که روش آموزش زیر مشخص است و مدل به خوبی به داده‌های جدید تعمیم نمی‌یابد. این نتیجه حتی در مورد داده هایی با فاصله زمانی کم بین آنها، حاشیه های زیادی برای بهبود بیشتر باقی می گذارد.

جدول ۷ نشان می دهد که چگونه نویز اضافه شده به ویژگی های نمودار پرس و جو بر نتایج در مرحله استنتاج تأثیر می گذارد. در اینجا می‌توانیم ببینیم که برخلاف روش پایه، توصیفگر مبتنی بر GCN نسبت به نویز نسبتاً قوی است، با مقادیر map@5 تا ۱۰ درصد کاهش می‌یابد در مقابل کاهش ۷۰ درصدی جستجوی ویژگی محلی پر سر و صدا Faiss. ما فقط نویز را به داده‌های یک منبع اضافه کردیم، با این فرض که داده‌های منبع متقاطع از قبل حاوی مقدار قابل توجهی نویز به دلیل فرآیند ضبط آنها هستند.

جدول ۸ پتانسیل تعمیم توصیفگرهای مبتنی بر GCN را برای مواردی نشان می‌دهد که داده‌ها از یک منبع می‌آیند و در مناطق جغرافیایی مختلف آموزش و آزمایش می‌شوند. توجه داشته باشید که map@5 برای جستجوی شباهت در دو بخش (آموزش) و یک (آزمایش) به ترتیب گزارش شده است. ما پیش از این، هایپرپارامترها را برای سناریوی یادگیری متقاطع تنظیم کردیم و می‌توانیم ببینیم که شبکه می‌تواند یک توصیفگر معنی‌دار برای منطقه جدیدی که در طول آموزش ندیده است ایجاد کند، بنابراین زمانی که داده‌ها از یکسان می‌آیند، به خوبی تعمیم می‌یابند. منبع

در نهایت، جدول ۹ نتایج یادگیری متقاطع منبع را نشان می دهد . این مدل از ابتدا آموزش داده شد، اما ما تمام پارامترها را از آزمایش های قبلی دست نخورده باقی گذاشتیم. نتایج به‌طور قابل‌توجهی کمتر از نتایج به‌دست‌آمده توسط سناریوی منبع مشابه است ، که نشان‌دهنده دشواری کار هدف‌گذاری شده، به‌ویژه برای داده‌هایی با فاصله زمانی قابل‌توجه است. به سختی می توان گفت دلیل کاهش عملکرد در این مورد چیست، زیرا هم ویژگی های هندسی و هم ساختار نمودار در مورد منبع متقاطع می توانند تأثیر زیادی بگذارند.داده ها. با این وجود، با در نظر گرفتن این واقعیت که حقیقت پایه مجموعه داده ما عمدتاً از منطبقات صحیح منفرد تشکیل شده است، نتایج جالب هستند و این شهود را تأیید می کنند که نمایش های نمودار می توانند برای این کار چالش برانگیز استفاده شوند.

جدول ۱۰ قابلیت تعمیم توصیفگرهای مبتنی بر GCN را برای مواردی که داده ها از دو منبع مختلف می آیند نشان می دهد. توجه داشته باشید که map@5 برای جستجوی شباهت در یک بخش (آموزش) و یک (تست) به ترتیب است. ما امتیاز نقشه@۵ کمتری نسبت به داده‌های متقابل منبع یکسان دریافت کردیم، اما نتیجه بالاتری داشتیم.

نتایج به‌دست‌آمده نشان می‌دهد که روش پیشنهادی برای سناریوهایی که با ویژگی‌های کمتر دقیق و داده‌های منبع متقاطع سروکار دارند، کار می‌کند و از رویکرد پایه بهتر عمل می‌کند : از این رو پتانسیل بیشتری برای کار تطبیق نمودار جغرافیایی واقعی مورد هدف ما دارد. جدول ۷ ثابت می کند که توصیفگرهای به دست آمده در برابر نویز قوی هستند و در ۵۰% پرس و جوها هنگام برخورد با داده های منبع یکسان (یعنی آموزش دیده و آزمایش شده در یک منطقه جغرافیایی) منطقه جغرافیایی صحیح را بازیابی می کنند. توجه داشته باشید که با خطوط پایه بدون نظارت، نویز به طور چشمگیری بر روی آن تأثیر می گذارد روی map@5 تأثیر می گذاردنتایج در حالی که مدل GCN ثابت می کند قوی است. در یک سناریوی دنیای واقعی، که در آن هنوز تولید خودکار نتایج کامل تقسیم‌بندی غیرممکن است، و حتی حاشیه‌نویسی انسانی ممکن است از فردی به فرد دیگر و از پایگاه‌داده‌ای به پایگاه داده دیگر متفاوت باشد، این ویژگی بسیار مهم است. با این حال، آزمایش‌های منبع متقاطع بسیار کم نشان داده‌اند نقشه@۵ارزش ها، اما نشان داد که رویکرد ما در وضعیت فعلی به اندازه کافی قابل تعمیم نیست. ما راه‌های مختلفی را برای نمایش داده‌های جغرافیایی به‌عنوان نمودار کاوش کردیم (گراف‌های Delaunay، نمودارهای RNG)، و پارامترهای مختلف مدل GCN سیامی خود را آزمایش کردیم و متوجه شدیم که معماری گراف و پارامترهای شبکه بسیار به یکدیگر وابسته هستند، اما ما مورد خاصی را کشف نکردیم. مشخصه روند برای تمام تست های انجام شده با گفتن آن، فرض می‌کنیم که اگرچه اولین نتایج به‌دست‌آمده هنوز در مورد روش‌های کلاسیک نیست، اما راهی به سمت یک جهت تحقیقاتی جدید است.

۷٫ پس زمینه

ایده استفاده از موجودیت‌های جغرافیایی مجزا برای فهرست‌بندی خودکار، تطبیق و انتخابی جغرافیایی‌سازی تصاویر هوایی جدید نیست. تحقیقات اولیه در Computer Vision مدت‌ها پیش آن را پیش‌بینی می‌کرد [ ۲۷ ]، و کارهای اخیر برای نمایه‌سازی و بازیابی مبتنی بر تصویر RS وجود دارد [ ۲۸ ، ۲۹ ]. با این حال، اکثر آثار اختصاص داده شده به تطبیق و بازیابی تصویر به صراحت از ساختار نمودار برای نشان دادن روابط فضایی بین موجودیت های جغرافیایی استفاده نمی کنند و همانطور که در این تحقیق با الهام از پیشرفت های اخیر در ساختار انجام می دهیم، هدف تطبیق متقاطع زمانی نیست. یادگیری. در ادامه پیشینه حوزه های مختلف تحقیقاتی را که کار کنونی بر آن استوار است، ارائه می دهیم.

۷٫۱٫ نمایش اطلاعات جغرافیایی به صورت نمودار

نمایش های مبتنی بر نمودار به طور سنتی برای نمایش شبکه جاده، قطار یا مسیر آب و محاسبات مرتبط با آنها مانند برنامه های مسیریابی استفاده می شود. آنها همچنین معمولا برای داده های جغرافیایی مکانی-زمانی استفاده می شوند [ ۳۰ ]. اما نمایش مبتنی بر نمودار از مکان‌ها و مناظر همچنین می‌تواند بینش‌های مهمی را در سناریوهایی مانند مکان‌یابی صحنه یا بازیابی اطلاعات جغرافیایی نشان دهد.

در ابتدا توسط گوگل برای توصیف بهبود موتور جستجوی خود با معناشناسی [ ۳۱ ] ابداع شد، اصطلاح “نمودار دانش” امروزه به طور گسترده برای اشاره به هر گونه نمایش مبتنی بر نمودار از دانش با هدف عمومی، مانند پایگاه های دانش بزرگ مرتبط استفاده می شود. ابر داده های باز (LOD)، یعنی DBPedia [ ۳۲ ]، Yago [ ۳۳ ]، و غیره. از روزهای اولیه وب داده ها، داده های جغرافیایی نقش اصلی را در ابر LOD ایفا کرده اند، زیرا آنها راهی بصری برای پیوند دادن ارائه می دهند. مجموعه داده هایی از زمینه های مختلف مانند علوم زیستی، علوم انسانی، میراث، رسانه ها، شبکه های اجتماعی و غیره [ ۳۴ ]. به دنبال مثال Ordnance Survey [ ۳۵]، بسیاری از آژانس های ملی نقشه برداری داده های جغرافیایی خود را در انطباق با شیوه ها و استانداردهای خوب Web of data منتشر کرده اند [ ۳۶ ، ۳۷ ، ۳۸ ، ۳۹ ]. به منظور گامی فراتر از ترجمه مستقیم داده‌های برداری جغرافیایی به یک نمودار RDF، [ ۴۰ ] مجموعه‌ای از روابط توپولوژیکی تقریبی تصفیه‌شده را برای غنی‌سازی نمودار دانش جغرافیایی و بهبود قابلیت‌های پاسخگویی به سؤالات پیشنهاد می‌کند. خلاصه نمودار دانش جغرافیایی تا حد زیادی در [ ۴۱ ] پوشش داده شده است. این کار موضوعاتی مانند درک، بازنمایی و استدلال در مورد POI را پوشش می‌دهد، اما راه‌هایی برای یادگیری توصیف‌گرهای منطقه جغرافیایی پیشنهاد نمی‌کند. در نهایت، Trisedya و همکاران. [ ۴۲] یک مدل هم ترازی موجودیت برای نمودارهای دانش بر اساس رویکرد محبوب قبلی Trans-E [ ۴۳ ] پیشنهاد می کند که روابط را با تفسیر آنها به عنوان ترجمه هایی که بر روی تعبیه های کم بعدی موجودیت ها کار می کنند مدل می کند. با این حال، این روش فقط برای پیوند ۱ به ۱ بین دو پایگاه داده گراف قابل استفاده است و از سه گانه به جای نمودار برای یادگیری جاسازی ها استفاده می کند، بنابراین نمی توان آن را مستقیماً در سناریوی ما استفاده کرد. در نهایت، لینگ کای و همکاران. [ ۴۴ ] یک چارچوب رمزگذار یکپارچه GCN به نام TransGCN را پیشنهاد می‌کند که می‌تواند تعبیه‌های موجودیت و تعبیه‌های روابط را به طور همزمان یاد بگیرد. کار مشابه ما در ایده استفاده از جاسازی نمودار برای رمزگذاری ساختار همسایه است. با این حال، نویسندگان تعبیه گره را هدف قرار می دهند و نه کل جاسازی گراف را مانند ما.

۷٫۲٫ هسته های نمودار و فاصله های نمودار

جستجوی شباهت بر اساس هسته های گراف یک موضوع تحقیقاتی شناخته شده با تعداد زیادی هسته های مختلف است که برای موارد خاص و انواع داده ها پیشنهاد شده است، بسیاری از آنها در کتابخانه Grakel [ ۴۵ ] موجود است. این شباهت معمولاً با تطابق دقیق (ایزومورفیسم نمودار کامل یا زیرگراف) [ ۴۶ ]، راه رفتن یا مسیرهای تصادفی روی نمودارها [ ۴۷ ]، انتشار اطلاعات در ساختار نمودار [ ۴۸ ] یا موارد دیگر تعریف می‌شود. یک بررسی اخیر در مورد هسته های گراف را می توان در [ ۴۹ ] یافت]. لازم به ذکر است که خود هسته ها به صورت دستی طراحی شده اند و با تئوری گراف برانگیخته می شوند و فقط برخی از آنها برای مدیریت ویژگی های پیوسته در لبه ها و گره های یک گراف طراحی شده اند. هسته‌های گراف را می‌توان به‌گونه‌ای فرمول‌بندی کرد که ابتدا بردارهای ویژگی را برای هر نمودار محاسبه می‌کنند، و سپس حاصلضرب درونی بین این بردارها را برای محاسبه مقدار هسته، بدون یادگیری به استثنای [ ۵۰ ] می‌گیرند. هسته های گراف خود را به عنوان ابزار بسیار کارآمدی برای مقایسه گراف نشان داده اند، اما اغلب زمان قابل توجهی برای محاسبه نیاز دارند.

فواصل گراف مهندسی شده یا آموخته شده بسیار شبیه به هسته گراف است. انتخاب های رایج شامل فواصل طیفی و فواصل بر اساس میل گره است. [ ۵۱ ] معیارهای رایج گراف و اندازه‌گیری‌های فاصله را مقایسه می‌کند و توانایی آن‌ها را در تشخیص ویژگی‌های توپولوژیکی رایج موجود در هر دو مدل نمودار تصادفی و شبکه‌های دنیای واقعی نشان می‌دهد. بسیاری از هسته‌های گراف کلاسیک نیز بر اساس فواصل نمودار هستند [ ۴۵ ، ۵۲ ]. اخیراً، فواصل نمودار توجه محققان را به خود جلب کرد، با کارهای اخیر که از مکانیسم‌های توجه برای ایجاد معیارهای قابل یادگیری استفاده می‌کنند [ ۵۳ ].

۷٫۳٫ جاسازی های نمودار

اخیراً الگوریتم‌های مختلف یادگیری ماشین و یادگیری عمیق برای داده‌های گراف پیشنهاد شده‌اند. جامعه داده کاوی علاقه زیادی به خلاصه کردن (دانش) نمودار دارد زیرا ساختار نمودار در همه جا وجود دارد: همه انواع داده ها از شبکه های اجتماعی و تا انتشارات تحقیقاتی را می توان به عنوان نمودار نشان داد. یک ایده رایج این است که تعبیه گره ها [ ۵۴ ] یا حتی کل نمودار [ ۵۵ ، ۵۶ ] را بر اساس ویژگی ها و ساختار آنها یاد بگیریم. همچنین نمونه ای از استفاده از چنین روش تعبیه گره در یک زمینه جغرافیایی وجود دارد. یان و همکاران [ ۵۷] تخمین شباهت و ارتباط انواع مکان با محیط اطرافشان را با استفاده از جاسازی انواع مکان پیشنهاد می کند. با این حال، همه این الگوریتم‌ها مبتنی بر مدل‌هایی هستند که از پردازش متن به دست می‌آیند، بنابراین برای تولید جاسازی‌هایی طراحی شده‌اند که گره‌هایی با همسایگی‌های شبکه مشابه در نزدیکی یکدیگر قرار می‌گیرند: گره‌ها به‌عنوان کلماتی که از یک واژگان گرفته شده‌اند، مدیریت می‌شوند. علاوه بر این، این روش‌ها می‌توانند اطلاعات ساختار یا برچسب‌گذاری را مدیریت کنند، اما نه هر دو را همزمان، که کاربرد آنها را برای سناریوی ما محدود می‌کند.

۷٫۴٫ شبکه های گراف کانولوشنال

در چند سال گذشته، شبکه‌های عصبی گراف (GNN) به‌عنوان یک کلاس مؤثر از مدل‌ها برای یادگیری نمایش داده‌های ساخت‌یافته و برای حل مسائل مختلف پیش‌بینی نظارت شده بر روی نمودارها ظهور کرده‌اند. چنین مدل‌هایی با طراحی نسبت به جایگشت عناصر گراف و محاسبه نمایش گره‌های گراف از طریق یک فرآیند انتشار که به طور مکرر اطلاعات ساختاری محلی را جمع‌آوری می‌کند، تغییرناپذیر هستند. گره‌های روی نمودارهای هم‌مورف (با ویژگی‌های گره و لبه‌های یکسان) بدون در نظر گرفتن ترتیب، نمایش‌های یکسانی خواهند داشت. شبکه‌های GNN دارای معماری‌های متفاوتی هستند و تقریباً می‌توان آنها را به چند دسته طبقه‌بندی کرد: روش‌های طیفی [ ۵۸ ]] پیچیدگی نمودار را با استفاده از بردارهای ویژه گراف لاپلاسین به عنوان ماتریس تبدیل، روش‌هایی که در حوزه فضایی کار می‌کنند [ ۱۶ ] و روش‌های مکمل GNN و آگنوستیک برای انتخاب خود GNN (یعنی ادغام، توجه) انجام می‌دهند. ۵۹ ]. GNN ها با موفقیت در بسیاری از حوزه ها از کشف دارو [ ۶۰ ] تا طبقه بندی شبکه های اجتماعی [ ۶۱ ] استفاده شده اند.]. مستقل از ماهیت شبکه، وظیفه مشترکی که توسط آنها انجام می شود، یادگیری تحت نظارت تعبیه گره ها است. سپس این نمایش گره ها یا مستقیماً برای طبقه بندی گره ها استفاده می شوند، یا در یک بردار گراف برای طبقه بندی گراف ادغام می شوند. مشکلات فراتر از طبقه بندی نظارت شده یا رگرسیون نسبتاً کمتر برای GNN ها مطالعه شده است. خو و همکاران [ ۶۲ ] ثابت کرد که با شبکه‌های عصبی کانولوشن، می‌توانیم شباهت نمودار را اندازه‌گیری کنیم، مانند آزمون تشابه Weisfeiler-Lehman. با این حال، مسئله ایزومورفیسم نمودار برای مورد استفاده ما چندان مرتبط نیست. رویکردهای یادگیری شباهت نمودار کلی تری اخیراً توسط [ ۶۳ و ۶۴ ارائه شده است]. این مدل های آموخته شده می توانند با معیارهای مورد نظر سازگار شوند و به طور بالقوه برای سناریوی هدف ما جالب هستند. با این حال، لی و همکاران. [ ۶۳ ] عملکرد روش را روی نمودارها تنها با تغییرات جزئی و بدون ویژگی گره نشان می دهد. در این مقاله، ما بر بازنمایی و یادگیری متریک شباهت برای نمودارهای نسبت داده شده که همان منطقه جغرافیایی را در طول زمان نشان می‌دهند، تمرکز می‌کنیم.

۷٫۵٫ شبکه های سیامی

هدف معماری‌های شبکه سیامی ساخت جاسازی‌هایی است، که در آن دو ویژگی استخراج‌شده مربوط به یک موجودیت دنیای واقعی، بیشتر شبیه به ویژگی‌هایی هستند که موجودیت‌های دنیای واقعی متفاوت را نشان می‌دهند [ ۶۵ ]. آنها یک انتخاب محبوب برای سناریوهایی هستند که با مشکلات یادگیری یکباره سروکار دارند، زمانی که یک نمونه آموزشی برای هر کلاس در دسترس است. کارایی شبکه‌های سیامی قبلاً برای ردیابی شی بصری [ ۶۶ ]، شناسایی مجدد شخص [ ۶۷ ]، تطبیق تصویر متقاطع [ ۶۸ ] و سایر وظایف نشان داده شده بود. شبکه های سیامی همچنین می توانند برای یادگیری شباهت نمودار استفاده شوند همانطور که در [ ۶۳ ] نشان داده شده است. نزدیکترین کار به ما کار اخیر [ ۶۹] که در آن نویسندگان با موفقیت از معماری Convolutional Graph Siamese برای نمایه سازی و بازیابی تصاویر سنجش از راه دور که به عنوان نمودارهای مجاورت منطقه نشان داده شده اند استفاده می کنند.

ما ایده مشابهی را دنبال می کنیم تا از قدرت توصیفی نمایش نمودار به همراه GCN مبتنی بر سیامی استفاده کنیم. با این حال، فرآیند ایجاد گراف با رویکرد گراف مجاورت منطقه (RAG) [ ۶۹ ] متفاوت است، و معماری پیشنهادی ما برای نوع داده‌ها و ویژگی‌های مربوطه در نظر گرفته شده است. سناریوی نهایی نیز متفاوت است: ما می‌خواهیم مکان دقیق را بازیابی کنیم نه کلاس‌های مشابه، از این رو با یک مشکل چالش برانگیزتر با بسیاری از کلاس‌ها و چند نمونه در هر کلاس (عمدتاً یک مکاتبه منفرد) سروکار داریم. علاوه بر این، هدف نهایی ما ایجاد یک تطابق داده تصویر به برداری است.

۸٫ نتیجه گیری

با در دسترس بودن رو به رشد حجم زیادی از داده های جغرافیایی تاریخی و مدرن با روش های مختلف (تصویر، داده های ساختاری یا متنی، و غیره)، توسعه یک چارچوب یکپارچه برای تجزیه و تحلیل مشترک آنها بسیار مورد توجه است. در این کار، ما شروع به حرکت به سمت چنین چارچوبی با بررسی مدل‌هایی برای یادگیری شباهت منطقه جغرافیایی کردیم که خود یک جهت تحقیق مرتبط است.

این مقاله رویکردی به مشکل نمایه‌سازی و بازیابی تصویر متقاطع عمودی از دیدگاه جدیدی پیشنهاد می‌کند: ما موجودیت‌های جغرافیایی نشان‌داده‌شده در عکس‌ها و ویژگی‌های هندسی و معنایی آنها را به عنوان یک نمودار متصل تفسیر می‌کنیم. سپس ما یک روش جدید مبتنی بر یادگیری عمیق را برای یادگیری نمایش نمودارهای موجودات جغرافیایی و روابط فضایی آنها و مقایسه آنها در طول زمان پیشنهاد کردیم. برای آزمایش این رویکرد، دو منبع اصلی و منبع متقاطع ایجاد کردیممجموعه داده ها مدل پیشنهادی مبتنی بر GCN در حال حاضر با روش بدون نظارت بر اساس شباهت ویژگی‌هایی که به عنوان خط پایه استفاده می‌کنیم، بهتر عمل می‌کند. اما بر خلاف این خط مبنا، مدل ما نسبت به وجود نویز در ویژگی‌ها قوی است، که آن را در یک سناریوی واقعی معتبر می‌کند، مانند نمایه‌سازی و بازیابی تصاویر هوایی تقسیم‌بندی شده و برداری خودکار یا حتی تطبیق پایگاه‌های داده بردار ناهمگن. وظیفه یا یک برنامه بازیابی الگوی مکانی-زمانی. ادغام داده‌های GIS و یادگیری ماشینی به ما این امکان را می‌دهد که با موفقیت مناطق جغرافیایی را در طول زمان مطابقت دهیم و در بیش از ۵۰٪ موارد، تا ۱۵ سال، تطابق صحیح را به دست آوریم. علاوه بر این، رویکرد پیشنهادی می‌تواند مستقیماً برای یادگیری تعبیه‌های گراف در هر مشکل شباهت گراف نسبت داده شده استفاده شود.

ما می بینیم که رویکرد پیشنهادی توسط مورخان و بایگانی‌هایی که با مقادیر زیادی از منابع بصری تاریخی کار می‌کنند و به دنبال راه‌هایی برای بازیابی تصاویر – عکس‌ها، نقشه‌ها، حکاکی‌ها، و غیره- هستند که همان مناطق جغرافیایی را نشان می‌دهند، یا مکان یابی این تصاویر را در زمانی که مکان ضعیف نشان داده شده است. با این حال، استفاده از رویکرد ما ساده نیست زیرا عکس‌های هوایی یا نقشه‌های باستانی به ندرت قطعه‌بندی می‌شوند، و روش پیشنهادی GisGCN به تقسیم‌بندی به عنوان مرحله قبلی نیاز دارد. می توان آن را به صورت دستی برای یک تصویر در زمان پرس و جو انجام داد، مشروط بر اینکه پایگاه داده از داده های برداری جغرافیایی باشد، همانطور که در این کار انجام می شود. برای مثال در مورد تطبیق بین مجموعه‌های تصاویر هوایی مورب، بهره‌برداری از داده‌های تصویری و برداری با هم پیچیده‌تر است. ما در اینجا دو احتمال را می بینیم. روش‌های تقسیم‌بندی خودکار مبتنی بر CNN دقت بیشتری به دست می‌آورند و می‌توان از آن‌ها برای حاشیه‌نویسی داده‌ها به عنوان گام قبلی استفاده کرد. روش دیگر استفاده از روش‌های یادگیری مبتنی بر گراف پیشنهادی است، اما گرفتن گره‌های گراف از طریق تشخیص شی. علاوه بر این، برخی از گره‌های اضافی را می‌توان برای ثبت حاشیه‌نویسی‌های متنی معرفی کرد که تا حدی در بسیاری از داده‌های تاریخی وجود دارد. با این حال، دشواری جدیدی در رمزگذاری ویژگی‌های متنی مانند نام‌های نام‌گذاری به همراه خواهد داشت، چالشی که ما برای تحقیقات آینده باقی می‌گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. و می توان از آنها برای حاشیه نویسی داده ها به عنوان گام قبلی استفاده کرد. روش دیگر استفاده از روش‌های یادگیری مبتنی بر گراف پیشنهادی است، اما گرفتن گره‌های گراف از طریق تشخیص شی. علاوه بر این، برخی از گره‌های اضافی را می‌توان برای ثبت حاشیه‌نویسی‌های متنی معرفی کرد که تا حدی در بسیاری از داده‌های تاریخی وجود دارد. با این حال، دشواری جدیدی در رمزگذاری ویژگی‌های متنی مانند نام‌های نام‌گذاری به همراه خواهد داشت، چالشی که ما برای تحقیقات آینده باقی می‌گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. و می توان از آنها برای حاشیه نویسی داده ها به عنوان گام قبلی استفاده کرد. روش دیگر استفاده از روش‌های یادگیری مبتنی بر گراف پیشنهادی است، اما گرفتن گره‌های گراف از طریق تشخیص شی. علاوه بر این، برخی از گره‌های اضافی را می‌توان برای ثبت حاشیه‌نویسی‌های متنی معرفی کرد که تا حدی در بسیاری از داده‌های تاریخی وجود دارد. با این حال، دشواری جدیدی در رمزگذاری ویژگی‌های متنی مانند نام‌های نام‌گذاری به همراه خواهد داشت، چالشی که ما برای تحقیقات آینده باقی می‌گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. اما گرفتن گره های گراف با استفاده از تشخیص شی. علاوه بر این، برخی از گره‌های اضافی را می‌توان برای ثبت حاشیه‌نویسی‌های متنی معرفی کرد که تا حدی در بسیاری از داده‌های تاریخی وجود دارد. با این حال، دشواری جدیدی در رمزگذاری ویژگی‌های متنی مانند نام‌های نام‌گذاری به همراه خواهد داشت، چالشی که ما برای تحقیقات آینده باقی می‌گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. اما گرفتن گره های گراف با استفاده از تشخیص شی. علاوه بر این، برخی از گره‌های اضافی را می‌توان برای ثبت حاشیه‌نویسی‌های متنی معرفی کرد که تا حدی در بسیاری از داده‌های تاریخی وجود دارد. با این حال، دشواری جدیدی در رمزگذاری ویژگی‌های متنی مانند نام‌های نام‌گذاری به همراه خواهد داشت، چالشی که ما برای تحقیقات آینده باقی می‌گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. چالشی که برای تحقیقات آتی باقی می گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند. چالشی که برای تحقیقات آتی باقی می گذاریم. یکی دیگر از کاربردهای مستقیم جالب کار ما، جستجوی پیکربندی‌های فضایی خاص (به عنوان مثال ساختمان‌هایی که بین جاده و رودخانه قرار گرفته‌اند) بدون توجه به موقعیت مکانی است که برای حرفه‌هایی مفید است که به مطالعه کاربری زمین، سازمان‌دهی فضا و شهرنشینی می‌پردازند.

در نهایت، هنوز تعدادی چالش جالب برای حل وجود دارد: بهبود کارایی مدل‌های تطبیق، مطالعه معماری‌های تطبیق مختلف، تطبیق GCN به گونه‌ای که بتواند از نمودارهایی با اندازه‌های مختلف استفاده کند، و استفاده از مدل ما در برنامه‌های جدید. دامنه ها ما فکر می‌کنیم که مدل‌های نمودار با توجه می‌توانند به طور موثر در برنامه مورد نظر کار کنند، و ما قصد داریم در آینده یک مکانیسم توجه اتخاذ کنیم. جهت ممکن دیگر بهبود نمایش نمودار است که می تواند به نتایج بازیابی بهتری منجر شود. ما این مسیرها را برای تحقیقات آتی واگذار می کنیم. ما همچنین منبع متقاطع جدید و مجموعه داده متقاطع را به همراه بارگذارهای داده (شامل تطبیق بارگذار داده برای کتابخانه هندسی Pytorch [ ۷۰ ) ارائه می کنیم.]). ما امیدواریم که این کار بتواند تحقیقات بیشتر در زمینه تطبیق نمودارهای جغرافیایی را تحریک کند و اولین معیار را برای یادگیری بر روی نمودارها برای تطبیق منطقه متقاطع ارائه دهد.

منابع

ISO ۱-۱۹۱۳۰: اطلاعات جغرافیایی – مدل‌های حسگر تصویر برای موقعیت‌یابی جغرافیایی – بخش ۱: مبانی. استاندارد بین المللی، سازمان بین المللی استاندارد. ۲۰۱۸٫ در دسترس آنلاین: http://www.iso.org (دسترسی در ۱۰ نوامبر ۲۰۲۰).
دومنیو، بی. عبادی، ن. Perret, J. ارزیابی دقت پلانیمتری اطلس های پاریس از اواخر قرن ۱۸ و ۱۹٫ در استخراج دانش از داده های جغرافیایی (KEGeoD)، مجموعه مقالات سمپوزیوم در محاسبات کاربردی (SAC 2018)، پائو، فرانسه، ۹-۱۳ آوریل ۲۰۱۸ ؛ ACM Press: Pau، فرانسه، ۲۰۱۸; جلد ۸، ص ۸۷۶–۸۸۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
جووردانو، اس. لو بریس، ای. مالت، سی. به سمت ارجاع جغرافیایی خودکار بررسی‌های فتوگرامتری هوایی آرشیوی. ایسپرس ان. فتوگرام از راه دور. حس اسپات. Inf. علمی ۲۰۱۸ ، IV-2 ، ۱۰۵-۱۱۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
چن، کیو. وانگ، ال. Waslander، SL; لیو، ایکس. چارچوب مدل‌سازی شکل سرتاسری برای تولید طرح کلی ساختمان بردار از تصاویر هوایی. ISPRS J. Photogramm. Remote Sens. ۲۰۲۰ , ۱۷۰ , ۱۱۴–۱۲۶٫ [ Google Scholar ] [ CrossRef ]
زو، ال. لی، ی. Shimamura، H. استخراج جاده و برداری از داده های تصویر هوایی. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی ۲۰۲۰ ، ۴۳ ، ۱۳۲۳-۱۳۲۷٫ [ Google Scholar ] [ CrossRef ]
مشارکت کنندگان Netronline. بزرگترین پایگاه داده تصاویر هوایی تاریخی ایالات متحده ۲۰۲۰٫ در دسترس آنلاین: https://www.historicaerials.com/ (در ۲۵ نوامبر ۲۰۲۰ قابل دسترسی است).
نه، اچ. آرائوجو، ا. سیم، جی. ویاند، تی. Han, B. بازیابی تصویر در مقیاس بزرگ با ویژگی‌های محلی عمیق و دقیق. در مجموعه مقالات کنفرانس بین المللی IEEE در بینایی کامپیوتر، ونیز، ایتالیا، ۲۲ تا ۲۹ اکتبر ۲۰۱۷؛ صص ۳۴۵۶–۳۴۶۵٫ [ Google Scholar ]
ماگلیانی، ف. Prati، A. یک بازیابی دقیق از طریق توصیفگرهای R-MAC+ برای تشخیص نقطه عطف. در مجموعه مقالات دوازدهمین کنفرانس بین المللی دوربین های هوشمند توزیع شده، آیندهوون، هلند، ۳ تا ۴ سپتامبر ۲۰۱۸؛ صص ۱-۶٫ [ Google Scholar ]
تیان، ی. چن، سی. شاه، م. تطبیق تصویر متقاطع برای مکان‌یابی جغرافیایی در محیط‌های شهری. در مجموعه مقالات کنفرانس IEEE در مورد دید رایانه و تشخیص الگو، هونولولو، HI، ایالات متحده آمریکا، ۲۱ تا ۲۶ ژوئیه ۲۰۱۷؛ صص ۳۶۰۸–۳۶۱۶٫ [ Google Scholar ]
شی، ی. یو، ایکس. لیو، ال. ژانگ، تی. Li, H. انتقال ویژگی بهینه برای مکان‌یابی جغرافیایی تصویر متقاطع. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، نیویورک، نیویورک، ایالات متحده آمریکا، ۷ تا ۱۲ فوریه ۲۰۲۰؛ جلد ۳۴، ص ۱۱۹۹۰–۱۱۹۹۷٫ [ Google Scholar ]
رگمی، ک. شاه، ام. پل زدن شکاف دامنه برای تطبیق تصویر زمین به هوایی. در مجموعه مقالات کنفرانس بین المللی IEEE/CVF در بینایی کامپیوتر، سئول، کره، ۲۷ تا ۲۸ اکتبر ۲۰۱۹؛ صص ۴۷۰-۴۷۹٫ [ Google Scholar ]
کاروالیو، آرسی کندی، دی.م. نیازی، ی. لیچ، سی. Konlechner، TM; Ierodiaconou، D. تجزیه و تحلیل فتوگرامتری ساختار از حرکت در عکاسی هوایی تاریخی: تعیین تغییر حجمی ساحل در مقیاس های دهه ای. زمین گشت و گذار. روند. Landforms ۲۰۲۰ , ۴۵ , ۲۵۴۰–۲۵۵۵٫ [ Google Scholar ] [ CrossRef ]
ون وستن، سی. Getahun، FL تجزیه و تحلیل تکامل زمین لغزش Tessina با استفاده از عکس های هوایی و مدل های ارتفاعی دیجیتال. ژئومورفولوژی ۲۰۰۳ ، ۵۴ ، ۷۷-۸۹٫ [ Google Scholar ] [ CrossRef ]
لی، ی. ما، جی. ژانگ، ی. بازیابی تصویر از داده های بزرگ سنجش از دور: یک بررسی. Inf. فیوژن ۲۰۲۱ ، ۶۷ ، ۹۴-۱۱۵٫ [ Google Scholar ] [ CrossRef ]
یوان، Q. شن، اچ. لی، تی. لی، ز. لی، اس. جیانگ، ی. خو، اچ. تان، دبلیو. یانگ، کیو. وانگ، جی. و همکاران یادگیری عمیق در سنجش از دور محیطی: دستاوردها و چالش ها سنسور از راه دور محیط. ۲۰۲۰ , ۲۴۱ , ۱۱۱۷۱۶٫ [ Google Scholar ] [ CrossRef ]
Kipf، TN; ولینگ، ام. طبقه بندی نیمه نظارت شده با شبکه های کانولوشن گراف. در مجموعه مقالات پنجمین کنفرانس بین المللی بازنمایی های یادگیری (ICLR 2017)، تولون، فرانسه، ۲۴ تا ۲۶ آوریل ۲۰۱۷٫ [ Google Scholar ]
توصیفگرهای شکل دوبعدی و سه بعدی مارتینز-اورتیز، CA. دکتری پایان نامه، دانشگاه اکستر، اکستر، انگلستان، ۲۰۱۰٫ [ Google Scholar ]
Delaunay، B. Sur la sphere vide. Izv. آکاد. Nauk SSSR، Otd. تشک. من Estestv. ناوک ۱۹۳۴ ، ۷ ، ۱-۲٫ [ Google Scholar ]
Knyazev، B. طبقه بندی نمودار با شبکه های کانولوشن گراف در PyTorch. ۲۰۱۸٫ در دسترس آنلاین: https://github.com/bknyaz/graph_nn (در ۱ فوریه ۲۰۲۰ قابل دسترسی است).
چن، تی. کورنبلیت، اس. نوروزی، م. هینتون، جی. چارچوبی ساده برای یادگیری متضاد بازنمایی های بصری. در مجموعه مقالات کنفرانس بین المللی یادگیری ماشین، وین، اتریش، ۱۲ تا ۱۸ ژوئیه ۲۰۲۰؛ صفحات ۱۵۹۷-۱۶۰۷٫ [ Google Scholar ]
Le Portail IGN. در دسترس آنلاین: https://geoservices.ign.fr/ (دسترسی در ۵ مه ۲۰۲۰).
مشارکت کنندگان OpenStreetMap. سیاره OSM Dumps. ۲۰۱۷٫ در دسترس آنلاین: https://planet.osm.org (در ۱ اوت ۲۰۲۰ قابل دسترسی است).
ترجان، RE کارایی یک الگوریتم اتحادیه مجموعه خوب اما نه خطی. J. ACM (JACM) ۱۹۷۵ ، ۲۲ ، ۲۱۵-۲۲۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Toussaint، GT نمودار همسایگی نسبی یک مجموعه مسطح محدود. تشخیص الگو ۱۹۸۰ ، ۱۲ ، ۲۶۱-۲۶۸٫ [ Google Scholar ] [ CrossRef ]
جانسون، جی. دوز، م. Jégou، H. جستجوی شباهت در مقیاس میلیارد با GPU. IEEE Trans. کلان داده ۲۰۱۹ ، ۷ ، ۵۳۵–۵۴۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Kingma، DP; با، جی. آدام: روشی برای بهینه سازی تصادفی. در مجموعه مقالات سومین کنفرانس بین المللی در مورد بازنمایی های یادگیری (ICLR 2015)، سن دیگو، کالیفرنیا، ایالات متحده آمریکا، ۷ تا ۹ مه ۲۰۱۵٫ [ Google Scholar ]
هالا، ن. ووسلمن، جی. شناخت الگوهای جاده و رودخانه با تطبیق رابطه ای. بین المللی قوس. فتوگرام Remote Sens. ۱۹۹۳ , ۲۹ , ۹۶۹٫ [ Google Scholar ]
لیو، ی. دینگ، ال. چن، سی. لیو، ی. یادگیری انتقال عمیق بدون نظارت مبتنی بر شباهت برای بازیابی تصویر سنجش از دور. IEEE Trans. Geosci. Remote Sens. ۲۰۲۰ , ۵۸ , ۷۸۷۲–۷۸۸۹٫ [ Google Scholar ] [ CrossRef ]
شائو، ز. ژو، دبلیو. دنگ، ایکس. ژانگ، ام. Cheng, Q. Multilabel بازیابی تصویر سنجش از دور بر اساس شبکه کاملاً کانولوشن. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. ۲۰۲۰ , ۱۳ , ۳۱۸–۳۲۸٫ [ Google Scholar ] [ CrossRef ]
سیاباتو، دبلیو. کلارامونت، سی. ایلاری، اس. Manso-Callejo، M.Á. بررسی روندهای مدلسازی در GIS زمانی کامپیوتر ACM. Surv. (CSUR) ۲۰۱۸ ، ۵۱ ، ۱-۴۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Singhal, A. معرفی نمودار دانش: اشیا، نه رشته ها. خاموش گوگل بلاگ ۲۰۱۲ ، ۵ . در دسترس آنلاین: https://www.blog.google/products/search/introducing-knowledge-graph-things-not/ (دسترسی در ۱۵ مه ۲۰۲۰).
لمان، جی. ایزل، آر. ژاکوب، م. جنتزش، آ. کونتوکوستاس، دی. مندز، PN; هلمن، اس. مورسی، ام. ون کلیف، پی. اور، اس. و همکاران DBpedia – یک پایگاه دانش چندزبانه در مقیاس بزرگ که از ویکی پدیا استخراج شده است. سمنت. وب ۲۰۱۵ ، ۶ ، ۱۶۷-۱۹۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شورشی، تی. سوشانک، اف. هافارت، جی. بیگا، جی. کوزی، ای. Weikum، G. YAGO: یک پایگاه دانش چند زبانه از ویکی‌پدیا، wordnet و geonames. در کنفرانس بین المللی وب معنایی ; Springer: Cham, Switzerland, 2016; صص ۱۷۷-۱۸۵٫ [ Google Scholar ]
شادبولت، ن. اوهارا، ک. برنرز لی، تی. گیبنز، ن. گلیزر، اچ. هال، دبلیو. داده‌های دولتی باز مرتبط: درس‌هایی از داده‌ها. دولت انگلستان. IEEE Intell. سیستم ۲۰۱۲ ، ۲۷ ، ۱۶-۲۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
گودوین، جی. دولبر، سی. هارت، جی. داده های مرتبط جغرافیایی: جغرافیای اداری بریتانیای کبیر در وب معنایی. ترانس. GIS ۲۰۰۸ ، ۱۲ ، ۱۹-۳۰٫ [ Google Scholar ] [ CrossRef ]
رونژین، اس. فولمر، ای. ماریا، پی. براتینگا، ام. بیک، دبلیو. لمنز، آر. van’t Veer, R. Kadaster Graph Knowledge: Beyond the Fifth Star of Open Data. اطلاعات ۲۰۱۹ ، ۱۰ ، ۳۱۰٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
دبروین، سی. میهن، ع. کلینتون، É. مک نرنی، ال. ناوتیال، ا. لاوین، پ. O’Sullivan، D. داده های مرتبط جغرافیایی معتبر ایرلند. در کنفرانس بین المللی وب معنایی ; Springer: برلین/هایدلبرگ، آلمان، ۲۰۱۷; صص ۶۶-۷۴٫ [ Google Scholar ]
د لئون، آ. ساکیسلا، وی. Vilches، LM; ویلازون-ترازاس، بی. پریاتنا، ف. Corcho، O. داده های مرتبط جغرافیایی: مورد استفاده اسپانیایی. در مجموعه مقالات ششمین کنفرانس بین المللی سیستم های معنایی، گراتس، اتریش، ۱-۳ سپتامبر ۲۰۱۰٫ صص ۱-۳٫ [ Google Scholar ]
اتمزینگ، جی. عبادی، ن. ترونسی، آر. Bucher، B. انتشار اطلاعات جغرافیایی مرجع در وب: فرصت ها و چالش ها برای IGN فرانسه. در مجموعه مقالات Terra Cognita 2014، ششمین کارگاه بین المللی درباره مبانی، فناوری ها و کاربردهای وب جغرافیایی، در ارتباط با سیزدهمین کنفرانس بین المللی وب معنایی، ریوا دل گاردا، ایتالیا، ۱۹ تا ۲۳ اکتبر ۲۰۱۴٫ [ Google Scholar ]
رگالیا، بی. یانوویچ، ک. مک‌کنزی، جی. محاسبات و پرس‌وجو روابط توپولوژیکی دقیق، تقریبی و متریک در داده‌های جغرافیایی مرتبط. ترانس. GIS ۲۰۱۹ ، ۲۳ ، ۶۰۱–۶۱۹٫ [ Google Scholar ] [ CrossRef ]
Yan, B. خلاصه نمودار دانش جغرافیایی. دکتری پایان نامه، دانشگاه کالیفرنیا، سانتا باربارا، کالیفرنیا، ایالات متحده آمریکا، ۲۰۱۹٫ [ Google Scholar ]
Trisedya، BD; چی، جی. Zhang, R. هم ترازی موجودیت بین نمودارهای دانش با استفاده از جاسازی ویژگی. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، هونولولو، HI، ایالات متحده، ۲۷ ژانویه تا ۱ فوریه ۲۰۱۹؛ جلد ۳۳، ص ۲۹۷–۳۰۴٫ [ Google Scholar ]
بوردس، آ. یوسونیر، ن. گارسیا-دوران، آ. وستون، جی. Yakhnenko، O. ترجمه تعبیه‌ها برای مدل‌سازی داده‌های چند رابطه‌ای. در پیشرفت در سیستم های پردازش اطلاعات عصبی ; Curran Associates Inc.: Red Hook، NY، USA، ۲۰۱۳; صص ۲۷۸۷–۲۷۹۵٫ [ Google Scholar ]
کای، ال. یان، بی. مای، جی. یانوویچ، ک. Zhu، R. TransGCN: فرضیات تبدیل جفت با شبکه های کانولوشن گراف برای پیش بینی پیوند. در مجموعه مقالات دهمین کنفرانس بین المللی جذب دانش، مارینا دل ری، کالیفرنیا، ایالات متحده آمریکا، ۱۹ تا ۲۱ نوامبر ۲۰۱۹؛ صص ۱۳۱-۱۳۸٫ [ Google Scholar ]
سیگلیدیس، جی. نیکولنتزوس، جی. لیمنیوس، اس. جیاتسیدیس، سی. اسکیانیس، ک. Vazirgiannis، M. GraKeL: A Graph Kernel Library در پایتون. جی. ماخ. فرا گرفتن. Res. ۲۰۲۰ ، ۲۱ ، ۱-۵٫ [ Google Scholar ]
کریگه، ن. Mutzel، P. هسته های تطبیق زیرگراف برای نمودارهای نسبت داده شده. در مجموعه مقالات بیست و نهمین کنفرانس بین المللی یادگیری ماشین (ICML’12)، حیفا، اسرائیل، ۲۱ تا ۲۴ ژوئن ۲۰۱۰٫ Omnipress: مدیسون، WI، ایالات متحده آمریکا، ۲۰۱۲؛ ص ۲۹۱-۲۹۸٫ [ Google Scholar ]
ویشواناتان، SVN؛ شرادولف، NN; کندور، آر. هسته های بورگوارد، KM Graph. جی. ماخ. فرا گرفتن. Res. ۲۰۱۰ ، ۱۱ ، ۱۲۰۱-۱۲۴۲٫ [ Google Scholar ]
نویمان، ام. گارنت، آر. باکیج، سی. Kersting، K. هسته های انتشار: هسته های نمودار کارآمد از اطلاعات منتشر شده. ماخ فرا گرفتن. ۲۰۱۶ ، ۱۰۲ ، ۲۰۹-۲۴۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کریگه، NM; یوهانسون، FD; موریس، سی. بررسی بر روی هسته گراف. Appl. شبکه علمی ۲۰۲۰ ، ۵ ، ۱-۴۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
یانارداق، پ. ویشواناتان، اس. هسته های گراف عمیق. در مجموعه مقالات بیست و یکمین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، سیدنی، استرالیا، ۱۰ تا ۱۳ اوت ۲۰۱۵٫ صص ۱۳۶۵–۱۳۷۴٫ [ Google Scholar ]
ویلز، پ. Meyer، FG Metrics برای مقایسه نمودار: راهنمای یک پزشک. PLoS ONE ۲۰۲۰ , ۱۵ , e0228728. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بورگوارد، KM; کریگل، هسته‌های کوتاه‌ترین مسیر HP در نمودارها. در مجموعه مقالات پنجمین کنفرانس بین المللی IEEE در مورد داده کاوی (ICDM’05)، هیوستون، TX، ایالات متحده، ۲۷-۳۰ نوامبر ۲۰۰۵٫ پ. ۸٫ [ Google Scholar ]
ژانگ، جی. گراف یادگیری متریک از راه دور عصبی با گراف-برت. arXiv ۲۰۲۰ ، arXiv:2002.03427. [ Google Scholar ]
گروور، ا. Leskovec, J. node2vec: یادگیری ویژگی های مقیاس پذیر برای شبکه ها. در مجموعه مقالات بیست و دومین کنفرانس بین المللی ACM SIGKDD در زمینه کشف دانش و داده کاوی، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، ۱۳ تا ۱۷ اوت ۲۰۱۶؛ صص ۸۵۵-۸۶۴٫ [ Google Scholar ]
ادیکاری، بی. ژانگ، ی. راماکریشنان، ن. Prakash، BA Sub2vec: یادگیری ویژگی برای زیرگراف ها. در کنفرانس اقیانوس آرام-آسیا در مورد کشف دانش و داده کاوی ؛ Springer: برلین/هایدلبرگ، آلمان، ۲۰۱۸; ص ۱۷۰-۱۸۲٫ [ Google Scholar ]
نارایانان، ع. چاندراموهان، م. ونکاتسان، ر. چن، ال. لیو، ی. Jaiswal, S. graph2vec: آموزش بازنمایی های توزیع شده نمودارها. در مجموعه مقالات سیزدهمین کارگاه بین المللی استخراج و یادگیری با نمودارها (MLG)، هالیفاکس، NS، کانادا، ۱۴ اوت ۲۰۱۷٫ [ Google Scholar ]
یان، بی. یانوویچ، ک. مای، جی. Gao, S. From itdl to place2vec: استدلال در مورد شباهت و ارتباط نوع مکان با یادگیری تعبیه‌ها از زمینه‌های فضایی تقویت‌شده. در مجموعه مقالات بیست و پنجمین کنفرانس بین‌المللی ACM SIGSPATIAL در مورد پیشرفت‌ها در سیستم‌های اطلاعات جغرافیایی، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، ۷ تا ۱۰ نوامبر ۲۰۱۷؛ صص ۱-۱۰٫ [ Google Scholar ]
برونا، جی. زارمبا، دبلیو. اسلم، آ. Lecun، Y. شبکه های طیفی و شبکه های متصل به صورت محلی روی نمودارها. در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی های یادگیری (ICLR2014)، Banff، AB، کانادا، ۱۴-۱۶ آوریل ۲۰۱۴٫ [ Google Scholar ]
ولیچکوویچ، پ. کوکورول، جی. کازانووا، آ. رومرو، آ. لیو، پی. Bengio، Y. گراف شبکه های توجه. در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی های یادگیری (ICLR2018)، ونکوور، BC، کانادا، ۳۰ آوریل تا ۳ مه ۲۰۱۸٫ [ Google Scholar ]
وسلکوف، ک. گونزالس، جی. الجیفری، س. گالیا، دی. میرنظامی، ر. یوسف، ج. برونشتاین، ام. Laponogov، I. HyperFoods: نقشه برداری هوشمند ماشینی از مولکول های ضد سرطان در غذاها. علمی جمهوری ۲۰۱۹ ، ۹ ، ۱-۱۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لی، جی. رانگ، ی. چنگ، اچ. منگ، اچ. هوانگ، دبلیو. هوانگ، جی. طبقه بندی گراف نیمه نظارت شده: دیدگاه گراف سلسله مراتبی. در کنفرانس جهانی وب ; انجمن ماشین‌های محاسباتی: نیویورک، نیویورک، ایالات متحده آمریکا، ۲۰۱۹؛ ص ۹۷۲-۹۸۲٫ [ Google Scholar ]
خو، ک. هو، دبلیو. Leskovec، J. جگلکا، اس. شبکه های عصبی نمودار چقدر قدرتمند هستند؟ در مجموعه مقالات کنفرانس بین المللی در مورد بازنمایی های یادگیری (ICLR2018)، ونکوور، BC، کانادا، ۳۰ آوریل تا ۳ مه ۲۰۱۸٫ [ Google Scholar ]
لی، ی. گو، سی. دالین، تی. وینیالز، او. کوهلی، پی. شبکه های تطبیق گراف برای یادگیری شباهت اشیاء ساختار یافته نمودار. در مجموعه مقالات تحقیقات یادگیری ماشینی، مجموعه مقالات سی و ششمین کنفرانس بین المللی یادگیری ماشین (ICML 2019)، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، ۹ تا ۱۵ ژوئن ۲۰۱۹؛ Chaudhuri, K., Salakhutdinov, R., Eds. Microtome Publishing: Brookline, MA, USA, 2019; جلد ۹۷، ص ۳۸۳۵–۳۸۴۵٫ [ Google Scholar ]
الرفو، ر. پروزی، بی. Zelle, D. Ddgk: یادگیری نمایش گراف برای هسته های گراف واگرایی عمیق. در کنفرانس جهانی وب ; انجمن ماشین‌های محاسباتی: نیویورک، نیویورک، ایالات متحده آمریکا، ۲۰۱۹؛ صص ۳۷-۴۸٫ [ Google Scholar ]
بروملی، جی. گیون، آی. LeCun، Y.; ساکینگر، ای. شاه، آر. تأیید امضا با استفاده از شبکه عصبی تأخیر زمانی «سیامی». در مجله بین المللی تشخیص الگو و هوش مصنوعی ; جهانی علمی: سنگاپور، ۱۹۹۳; جلد ۷، ص ۶۶۹–۶۸۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لی، بی. یان، جی. وو، دبلیو. زو، ز. Hu, X. ردیابی بصری با کارایی بالا با شبکه پیشنهادی منطقه سیامی. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ صفحات ۸۹۷۱-۸۹۸۰٫ [ Google Scholar ]
چانگ، دی. طاهب، ک. Delp، EJ یک شبکه عصبی کانولوشنال سیامی دو جریانی برای شناسایی مجدد افراد. در مجموعه مقالات کنفرانس بین المللی IEEE در بینایی کامپیوتر، ونیز، ایتالیا، ۲۲ تا ۲۹ اکتبر ۲۰۱۷؛ صفحات ۱۹۸۳-۱۹۹۱٫ [ Google Scholar ]
هو، اس. فنگ، ام. نگوین، آر.ام. Hee Lee, G. Cvm-net: شبکه تطبیق متقاطع برای مکان‌یابی زمین به هوایی مبتنی بر تصویر. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو، سالت لیک سیتی، UT، ایالات متحده آمریکا، ۱۸ تا ۲۳ ژوئن ۲۰۱۸؛ صص ۷۲۵۸-۷۲۶۷٫ [ Google Scholar ]
چاودوری، یو. بانرجی، بی. Bhattacharya، A. شبکه کانولوشن گراف سیامی برای بازیابی تصویر سنجش از راه دور مبتنی بر محتوا. محاسبه کنید. Vis. تصویر زیر. ۲۰۱۹ ، ۱۸۴ ، ۲۲-۳۰٫ [ Google Scholar ] [ CrossRef ]
فی، م. لنز، JE آموزش بازنمایی سریع نمودار با PyTorch Geometric. در مجموعه مقالات کنفرانس بین المللی بازنمودهای یادگیری، کارگاه آموزشی بازنمایی در نمودارها و منیفولدها، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، ۶ مه ۲۰۱۹٫ [ Google Scholar ]
پیوند و بهره برداری پیشرفته از میراث نمادین جغرافیایی دیجیتالی شده. در دسترس آنلاین: https://www.alegoria-project.fr/en/GENR_dataset (در ۲۸ اکتبر ۲۰۲۱ قابل دسترسی است).

شکل ۱٫ رویکرد پیشنهادی GisGCN از چندین مرحله تشکیل شده است: (۱) انتخاب POI و مناطق جغرافیایی اطراف برای داده های متقاطع. (۲) برای هر منطقه جغرافیایی، نمایش نهادهای جغرافیایی آن به عنوان یک نمودار برچسب دار متصل؛ (۳) برای هر نمودار، یادگیری تعبیه‌شده مبتنی بر GCN با وزن‌های مشترک. (۴) بازیابی بر اساس شباهت مناطق جغرافیایی در طول زمان.

شکل ۲٫ مراحل اصلی رویکرد پیشنهادی GisGCN بر روی نمودارها: آموزش و ارزیابی.

شکل ۳٫ معماری شماتیک مدل پیشنهادی برای آموزش تعبیه‌های گراف.

شکل ۴٫ عکس‌های لحظه‌ای موقتی که با یک عکس ارتوفوگرافی مربوط به سال ۲۰۲۰ همپوشانی دارند. ساختمان‌هایی که در تاریخ‌های مختلف گرفته شده‌اند با خطوط سبز و سفید برای سال ۲۰۰۴ و رنگ‌های رز و بژ برای سال ۲۰۱۹ نشان داده شده‌اند. بعد.

شکل ۵٫ نمونه ای از جعبه های محدود کننده یک سطح مساوی در اطراف POI. توجه داشته باشید که اگر دو جعبه کراندار بیش از ۵۰% همپوشانی داشته باشند، آنها را نمایانگر یک منطقه جغرافیایی می‌دانیم.

شکل ۶٫ نمونه ای از نمودارهای به دست آمده که منطقه جغرافیایی یکسان را در دو نقطه زمانی مختلف نشان می دهد. ( سمت چپ ): ۲۰۰۴٫ ( راست ): ۲۰۱۹٫ هندسه های دقیق برای مرجع نشان داده شده است، دسته بندی های آنها دارای کد رنگی هستند: قرمز = ساختمان، نارنجی = بخش جاده، زرد = ساختمان از یک دسته خاص (مانند کلیسا، بنای تاریخی) ، قلعه و غیره).

شکل ۷٫ نمودارهای حاصل برای نمودار شماره ۱۷٫ ( سمت چپ ): OSM 2020، ( وسط ): IGN 2019. برچسب های گره دارای کد رنگی هستند: قرمز = ساختمان ها، نارنجی: جاده ها، بنفش: راه آهن. ( راست ): نمودارهای IGN (نارنجی) و OSM (آبی) روی هم قرار گرفته اند.

شکل ۸٫ ( سمت چپ ): نمودارهای روی هم گذاشته OSM 2020 (آبی) و IGN 2004 (نارنجی). ( سمت راست ): نمودارهای روی هم قرار داده شده OSM 2020 و IGN 2019. منطقه جغرافیایی یکسان در طول سال ها و منابع.

شکل ۹٫ هیستوگرام های IOU برای تطبیق مناطق جغرافیایی نمودار به دست آمده برای بخش Meurthe-en-Moselle. اگر تمام ویژگی‌های گره‌ها دقیقاً مطابقت داشته باشند (تطبیق تزریقی) در نمودارها، مقدار IOU 1 خواهد بود.

شکل ۱۰٫ هیستوگرام های IOU برای تطبیق مناطق جغرافیایی نمودار به دست آمده برای بخش Meurthe-et-Moselle برای دو منبع نمودار: IGN 2019 و OSM 2020. سطح دقت ویژگی ها در ۳ ثابت شده است.

شکل ۱۱٫ IOU ( a ) هیستوگرام بین داده های IGN و OSM 2019-2020، با d متغیر . ( ب ) هیستوگرام های IOU برای تطبیق مناطق جغرافیایی نمودار به دست آمده برای بخش Meurthe-en-Moselle برای دو منبع نمودار (IGN 2019-OSM 2020) و ۴ دسته مختلف: قرمز-ساختمان های معمولی، زرد-همه ساختمان ها (از جمله بناهای تاریخی)، آبی- رودخانه ها و جاده های سیاه

شکل ۱۲٫ نمونه ای از ۵ نمودار مشابه برتر صحیح در سال ۲۰۱۰ برای پرس و جو از سال ۲۰۲۰، پایگاه داده متقاطع برگردانده شد. رنگ های گره بیانگر معنایی موجودیت های جغرافیایی است.

شکل ۱۳٫ نمونه ای از نمودار نمایش منطقه جغرافیایی تقریباً یکسان در طول ۴ سال.

هوش مکانی اتیم تحقیقاتی ونوس نصیرفام