نقشه برداری از choropleth دو متغیره
روش نگاشت بردار ورودی در شبکه به این صورت است که گره ای را با نزدیک ترین یا مشابه ترین بردار وزن به بردار ورودی پیدا کنید و مختصات شبکه این گره را به بردار ورودی اختصاص دهید. در جایی که وزن گره با بردار ورودی مطابقت دارد، آن ناحیه از شبکه به طور انتخابی بهینه می شود تا شباهت بیشتری به داده های کلاسی که بردار ورودی به آن تعلق دارد داشته باشد. از توزیع اولیه وزنهای تصادفی، و در طی چندین تکرار، SOM در نهایت در نقشهای از مناطق پایدار که توسط گرههای همسایه مشابه تشکیل شده است، قرار میگیرد. هر منطقه به طور موثر یک طبقه بندی ویژگی است. هر بردار ورودی جدید و دیده نشده ای که به SOM ارائه شود، گره هایی را در منطقه با بردارهای وزن مشابه تحریک می کند. بنابراین، SOM به طور خودکار بردار ورودی جدید را طبقه بندی می کند. مجموعه گره ها را می توان به عنوان یک نمودار شباهت و SOM از توزیع اقلام داده شده تشکیل می دهد. فرآیند SOM شامل چندین مرحله در چندین تکرار است :
- مقدار بردارهای وزن را برای هر گره آغاز کنید.
- بردار ورودی را به طور تصادفی از مجموعه داده های آموزشی انتخاب کنید.
- هر گره را بررسی کنید تا مشخص شود که بردار وزن آن چقدر شبیه بردار ورودی است. گره ای که وزن آن بیشتر شبیه بردار ورودی است برنده یا بهترین گره منطبق اعلام می شود.
- شعاع همسایگی بهترین گره منطبق را محاسبه کنید و هر گره ای را در این شعاع که در محله برنده تصور می شود پیدا کنید.
- وزن هر گره همسایه را تنظیم کنید تا شبیه بردار ورودی شود. هرچه یک گره به بهترین گره منطبق باشد، وزن آن بیشتر تغییر می کند.
- مراحل ۲ تا ۵ را برای تکرارهای N تکرار کنید.
فرض کنید ![]() باشد که بردار ورودی m بعدی است و
باشد که بردار ورودی m بعدی است و ![]() که بردار وزن مربوط به ابعاد m برای گره j است، که در آن n تعداد گره ها در لایه محاسباتی است. مقداردهی اولیه عبارت است از مقداردهی اولیه بردارهای وزن برای هر گره با مقادیر تصادفی استاندارد شده کوچک که معمولا شباهت بین بردار ورودی و گره توسط تابع متمایز تعیین می شود. این تابع به عنوان فاصله اقلیدسی بین بردار ورودی X و بردار وزن Wj برای هر گره j تعریف می شود که به صورت زیر محاسبه می شود :
که بردار وزن مربوط به ابعاد m برای گره j است، که در آن n تعداد گره ها در لایه محاسباتی است. مقداردهی اولیه عبارت است از مقداردهی اولیه بردارهای وزن برای هر گره با مقادیر تصادفی استاندارد شده کوچک که معمولا شباهت بین بردار ورودی و گره توسط تابع متمایز تعیین می شود. این تابع به عنوان فاصله اقلیدسی بین بردار ورودی X و بردار وزن Wj برای هر گره j تعریف می شود که به صورت زیر محاسبه می شود :

برای هر بردار ورودی، گره ها مقادیر مربوط به تابع تشخیصی را محاسبه می کنند. گره با کوچکترین مقدار، بهترین گره منطبق اعلام می شود – یعنی بردار وزن آن بیشتر شبیه بردار ورودی است.
پس از تعیین بهترین گره تطبیق، مرحله بعدی محاسبه اینکه کدام یک از گره های دیگر در همسایگی آن قرار دارند است. محله اغلب در عمل با تابع گاوسی تعریف می شود که به صورت زیر بیان می شود :

غالباً در عمل با عملکرد گوسی به صورت زیر تعریف می شود :
که در اینجا rw و rj موقعیت بهترین گره و گره j منطبق در محله روی شبکه هستند، || rw – rj || فاصله اقلیدسی بین دو گره است و σ نشان دهنده دامنه موثر یا اندازه محله است (یین، ۲۰۰۸). این تابع محله دارای چندین ویژگی مهم است : حداکثر در بهترین گره منطبق است، در مورد آن گره متقارن است، به طور یکنواخت با صفر شدن فاصله تا بی نهایت کاهش می یابد و مستقل از مکان بهترین گره منطبق است. علاوه بر این ویژگی خاص SOM ها این است که مساحت محله با گذشت زمان کاهش می یابد. وابستگی متداول به زمان فروپاشی نمایی است :
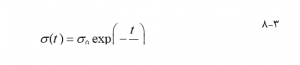
که در اینجا σ۰ عرض محله را در ابتدای فرآیند نشان می دهد (معمولاً روی “شعاع” شبکه تنظیم می شود) ، t- گام زمانی فعلی (تکرار حلقه) و λ ثابت زمان است. به عبارت دیگر مساحت محله به مرور زمان کوچک می شود.
نکته محله این است که گره برنده نه تنها وزنه های خود را به روز می کند، بلکه همسایگان آن نیز وزنه های خود را به روز می کنند، هرچند نه به اندازه خود برنده. در عمل اگر گره در مجاورت یافت شود، بردار وزن آن مطابق معادله زیر تنظیم می شود :
که در اینجا t گام زمانی را نشان می دهد و α (t) میزان یادگیری نامیده می شود که با گذشت زمان کاهش می یابد. اساساً این معادله نشان می دهد که وزن تنظیم شده جدید گره j برای ورودی i برابر با وزن قدیمی به علاوه کسری از تفاوت بین وزن قدیم و ورودی است.
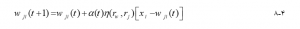
فروپاشی نرخ یادگیری در هر تکرار با استفاده از معادله زیر محاسبه می شود :

![]() به طور کلی با مقادیر بین ۴/۰ و ۱/۰ مقداردهی اولیه می شود. سپس به تدریج در طول زمان تحلیل می رود به طوری که در چند تکرار آخر نزدیک به صفر است. اثر هر به روز رسانی وزن این است که بردارهای وزن گره برنده و گره های مجاور آن را به سمت بردار ورودی حرکت می دهد. ارائههای مکرر دادههای آموزشی منجر به ترتیب توپولوژیکی میشود که در آن وزنهای کل محله در جهت حرکت میکنند و اقلام داده مشابه تمایل دارند گرههای مجاور را تحریک کنند. بنابراین، SOM نقشه معنایی را تشکیل می دهد که در آن اقلام داده مشابه در نزدیکی یکدیگر نگاشته می شوند و موارد نامتعارف در فاصله بین آنها قرار می گیرد. همانطور که در تصویر شکل ۸-۲۳ نشان داده شده است، ممکن است توسط شبکه شش ضلعی در سایه های مختلف خاکستری یا رنگها تجسم شود. هر شش ضلعی نشان دهنده یک گره در SOM است. مقیاس خاکستری یا رنگ یا شدت رنگ شش ضلعی نشان دهنده فاصله اقلیدسی بین بردار وزن شش ضلعی و بردارهای وزن شش ضلعی های مجاور آن است. به طور معمول ، رنگهای روشن بردارهای وزن گره را با فاصله بسیار نزدیک نشان می دهند (یعنی بردارهای داده چند متغیره مشابه) و رنگهای تیره تر نشان دهنده بردارهای وزن گره هستند که به طور گسترده تری از هم جدا شده اند (یعنی بردارهای داده چند متغیره متفاوت). بنابراین مناطق رنگ روشن به عنوان خوشه و مناطق تیره به عنوان مرز بین خوشه ها در نظر گرفته می شوند. این نوع نمایش گرافیکی ماتریس فاصله یکپارچه نامیده می شود که معمولاً به عنوان ماتریس U شناخته می شود ( اولسچ و سیمون، ۱۹۹۰). این نمودار شباهت داده های ورودی را ارائه می دهد و می تواند به تجسم خوشه ها در مجموعه داده های چند بعدی و چند بعدی کمک کند.
به طور کلی با مقادیر بین ۴/۰ و ۱/۰ مقداردهی اولیه می شود. سپس به تدریج در طول زمان تحلیل می رود به طوری که در چند تکرار آخر نزدیک به صفر است. اثر هر به روز رسانی وزن این است که بردارهای وزن گره برنده و گره های مجاور آن را به سمت بردار ورودی حرکت می دهد. ارائههای مکرر دادههای آموزشی منجر به ترتیب توپولوژیکی میشود که در آن وزنهای کل محله در جهت حرکت میکنند و اقلام داده مشابه تمایل دارند گرههای مجاور را تحریک کنند. بنابراین، SOM نقشه معنایی را تشکیل می دهد که در آن اقلام داده مشابه در نزدیکی یکدیگر نگاشته می شوند و موارد نامتعارف در فاصله بین آنها قرار می گیرد. همانطور که در تصویر شکل ۸-۲۳ نشان داده شده است، ممکن است توسط شبکه شش ضلعی در سایه های مختلف خاکستری یا رنگها تجسم شود. هر شش ضلعی نشان دهنده یک گره در SOM است. مقیاس خاکستری یا رنگ یا شدت رنگ شش ضلعی نشان دهنده فاصله اقلیدسی بین بردار وزن شش ضلعی و بردارهای وزن شش ضلعی های مجاور آن است. به طور معمول ، رنگهای روشن بردارهای وزن گره را با فاصله بسیار نزدیک نشان می دهند (یعنی بردارهای داده چند متغیره مشابه) و رنگهای تیره تر نشان دهنده بردارهای وزن گره هستند که به طور گسترده تری از هم جدا شده اند (یعنی بردارهای داده چند متغیره متفاوت). بنابراین مناطق رنگ روشن به عنوان خوشه و مناطق تیره به عنوان مرز بین خوشه ها در نظر گرفته می شوند. این نوع نمایش گرافیکی ماتریس فاصله یکپارچه نامیده می شود که معمولاً به عنوان ماتریس U شناخته می شود ( اولسچ و سیمون، ۱۹۹۰). این نمودار شباهت داده های ورودی را ارائه می دهد و می تواند به تجسم خوشه ها در مجموعه داده های چند بعدی و چند بعدی کمک کند.
گوو و همکاران (۲۰۰۵) رویکردی را برای ادغام PCP ها و SOM ها در نقشه برداری چند متغیره پیشنهاد کرد. با رویکرد خود، SOM موارد داده (ویژگی هایی مانند واحد های نقشه برداری و واحد های آماری) را به گره ها اختصاص می دهد و گره ها را مطابق با طرح رنگی سیستماتیک طراحی می کند تا گره های نزدیک یا مشابه رنگهای مشابه داشته باشند. گره ممکن است چندین مورد داده را به خود اختصاص دهد یا هیچ مورد داده ای نداشته باشد. SOM خود مقادیر داده اصلی را نشان نمی دهد. اما گره با آیتم های داده شامل چهار قطعه اطلاعات است: آیتم های داده به گره، تعداد آیتم های داده در گره، بردار میانگین (میانگین مقادیر همه آیتم های داده) و رنگ گره اختصاص داده شده است. این قطعات از اطلاعات توسط PCP برای ترسیم خطوط مشخصات هر مورد داده استفاده می شود. سپس هر مورد داده (نه هر گره) نقشه برداری می شود، از نظر جغرافیایی با رنگ اختصاص داده شده به گره ای که شامل مورد داده است. این نقشه یک نقشه چند متغیره است که به گره های غیر خالی موجود در ماتریس U SOM و پروفایل های PCP متصل شده است. از دیدگاه نقشه برداری موضوعی، SOM به عنوان روش طبقه بندی چند متغیره عمل می کند، رنگ ها را برای نگاشت ارائه می دهد و PCP به عنوان علائم عمل می کند، معانی آن رنگ ها را ارائه می دهد. این امر درک داده های چند متغیره و کشف توزیع مکانی الگوهای مختلف چند متغیری را آسان می کند.

شکل ۸-۲۳ ماتریس U
مثلا شکل ۸-۲۴ نقشه چند متغیره از چهار ویژگی خاک (یعنی چهار متغیر) و SOM و PCP مرتبط آن را نشان می دهد که از جدول ۸-۱ با استفاده از نرم افزار نقشه برداری چند متغیره سومویس ( گیوع، ۲۰۰۸) ایجاد شده است. در ماتریس U، دایره مقیاس شده در شش ضلعی گره، تعداد آیتم های داده را در گره نشان می دهد. هر دایره با یک رنگ پر شده است. این رنگ برای ترسیم خطوط مشخصات اقلام داده (واحدهای نقشه برداری خاک) موجود در گره در PCP و برای ترسیم موارد داده بر روی نقشه ویژگی خاک استفاده می شود. رنگهای مشابه در PCP و نقشه نشان دهنده شباهتهای چهار ویژگی خاک (متغیرهای ورودی) است. ضخامت خط پروفایل در PCP نیز به تعداد کل داده های موجود در گره مقیاس می شود. با تفسیر PCP، توزیع چهار ویژگی خاک در هر واحد نقشه برداری قابل درک است. نقشه در واقع یک نقشه چند متغیره با چهار متغیر است. کادر ۸-۷ نشان می دهد که چگونه SOMVIS برای تولید سه نمایشگر در شکل ۸-۲۴ استفاده می شود.
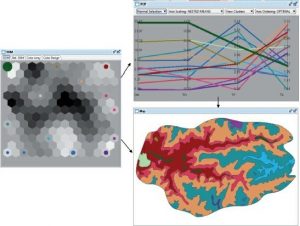
شکل ۸-۲۴ نقشه برداری چند متغیره با SOM و PCP

