مدل سازی روابط مکانی
الگوهای مکانی ناشی از فرآیندهای برون زا (القایی) یا درون زا (ذاتی) هستند که در مکان و زمان رخ میدهند. خود همبستگی مکانی تا حد زیادی تأثیر فرآیندهای درون زا است. به عنوان مثال فرآیندهای درون زا مانند پراکندگی بذر، جریان ژنی و رقابت تمایل دارند که گیاهان درون تکه ای شبیه یکدیگر باشند. بیشتر پدیدههای محیطی درجاتی از خودهمبستگی مکانی را نشان میدهند که میتوان آن را با استفاده از Moran’s I و سایر آمارهای مورد بحث در دو بخش قبل اندازهگیری کرد. الگوی مکانی ناشی از فرایندهای برون زا، عملکرد عوامل دیگر مستقل از متغیر یا ویژگیهای مورد علاقه است. به عنوان مثال الگوی بارش ممکن است تابعی از ارتفاع و فاصله از دریا باشد. الگوی مکانی گیاهان ممکن است پاسخی به خاکها باشد، زیرا ممکن است فقط در نوع خاصی از خاک رشد کنند. توزیع مکانی حیوانات حیات وحش ممکن است با عوامل محیطی مانند بارندگی، درجه حرارت یا نوع زیستگاه که خود از لحاظ مکانی با یکدیگر ارتباط دارند، محدود شده یا به طور فعال پاسخ دهد. چنین الگوهای مکانی را میتوان با استفاده از رگرسیون بررسی و مدل سازی کرد.
رگرسیون ابزار آماری است که برای بررسی و برآورد روابط بین متغیرها استفاده میشود. از آن به عنوان وسیله اصلی ارزیابی روابط مکانی به منظور توضیح عوامل پشت الگوهای مکانی مشاهده شده استفاده شده است. رگرسیون ساده یا چندگانه سنتی برای کشف، بررسی و مدل سازی روابط مکانی با فرض ثابت بودن و یکنواخت بودن روابط در کل منطقه مورد استفاده قرار میگیرد. رگرسیون با وزن جغرافیایی تغییرات مکانی یا منطقه ای روابط را در نظر میگیرد.
رگرسیون ساده
رگرسیون ساده روابط بین دو متغیر را با استفاده از معادله خطی زیر مدل میکند :

در این معادله رگرسیون، y متغیر وابسته، x متغیر مستقل یا توضیحی، a و b ضرایب رگرسیون و ε عبارت خطا هستند. ضرایب رگرسیون بیانگر شکل و قدرت رابطه متغیر توضیحی با متغیر وابسته است. از آنجایی که بعید است هنگام بررسی پدیدههای دنیای واقعی با یک رابطه خطی کامل مواجه شویم، ε همیشه وجود دارد. هدف از تحلیل رگرسیون ساده بدست آوردن تخمینی از پارامترهای مجهول a و b و ارزیابی باقیماندهها است. هنگامی که ضرایب رگرسیون شناخته شد، مقادیر y را میتوان از مقادیر x توسط رابطه زیر محاسبه کرد :

که در آن Y مقدار y تخمینی یا پیش بینی شده است. به عنوان مثال، فرض کنید رگرسیون بارندگی سالانه (y) در تعداد روزهای بارانی سالانه (x) مدل زیر را ایجاد میکند :
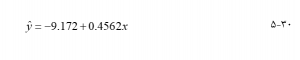
فرض کنید تعداد کل روزهای بارانی سال آینده پنجاه روز پیش بینی میشود. سپس بارندگی سالانه پیش بینی شده ۱۷۲/۹- + ۴۵۶۲/۰ × ۵۰ = ۶۳۸/۱۳ اینچ است. اگر تعداد روزهای بارانی سال آینده به هفتاد روز تغییر یابد، تخمین بارندگی سالانه ۹٫۱۷۲- + ۰٫۴۵۶۲ × ۷۰ = ۲۲٫۷۶۲ اینچ است.
فرض کنید تعداد کل روزهای بارندگی سال آینده پنجاه بار پیش بینی شده است. سپس بارندگی سالانه پیش بینی شده ۱۷۲/۹- + ۴۵۶۲/۰ × ۵۰ = ۶۳۸/۱۳ اینچ است. اگر تعداد روزهای بارندگی سال آینده به هفتاد مورد تجدید نظر شود ، برآورد سالانه بارندگی -۹٫۱۷۲ + ۰٫۴۵۶۲ ۰٫ ۷۰ = ۲۲٫۷۶۲ اینچ است.
ضرایب رگرسیون بر اساس مجموعه ای از دادههای نمونه زوجی از متغیرهای وابسته و توضیحی برآورد میشود. شکل رابطه بین دو متغیر را میتوان با ترسیم دادههای نمونه (اندازه گیریهای جفتی x و y برای هر مشاهده) در نمودار پراکنده، همانطور که در شکل ۵-۱۹ به صورت گرافیکی نشان داد. هر نقطه در نمودار نشان دهنده یک مشاهده با مقدار x و یک مقدار y است. رگرسیون ساده شامل برازش یک خط مستقیم به مجموعه نقاط است به طوری که مجموع فواصل عمودی مجذور از نقاط منفرد تا خط کوچکتر از هر خط دیگری باشد، یعنی به حداقل برسد (شکل ۱۹-۵) که در آن :

yi مقدار y اندازه گیری شده مشاهده iام است و yi مقدار y آن است که توسط خط مستقیم تخمین زده یا پیش بینی میشود. ei باقیمانده نامیده میشود. خط مستقیم را خط رگرسیون حداقل مربعات یا به سادگی خط رگرسیون مینامند. ضریب رگرسیون a نقطه قطع خط روی محور y است (مقدار y در نقطه ای که x برابر با صفر است) و b شیب خط رگرسیون است. آنها با استفاده از دادههای نمونه به شرح زیر تعیین میشوند :
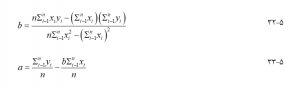
با خط رگرسیون پیشبینی میشود، y=y وقتی x=x است، میانگین x و y به ترتیب کجا هستند. این بدان معناست که نقطه (, ) روی خط رگرسیون قرار دارد. این برای همه مسائل رگرسیون خطی صادق است. تغییر در مقادیر مشاهده شده متغیر وابسته y دارای دو جزء است : باقیمانده ای که توسط متغیر مستقل x توضیح داده نشده یا به حساب نمیآید، و انحراف مقدار y پیش بینی شده از آن با x توضیح داده شده است، همانطور که در شکل ۵-۱۹ نشان داده شده است کسری از تغییرات کل در y که با رگرسیون توضیح داده میشود، ضریب تعیین نامیده میشود و محاسبه میشود :

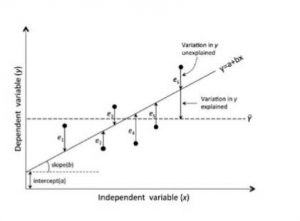
شکل ۵-۱۹ رگرسیون ساده و مفاهیم مرتبط
مقدار r2 در محدوده بین صفر و ۱ است. مقدار صفر نشان میدهد که هیچ یک از تغییرات در y با x توضیح داده نمیشود، در حالی که مقدار ۱ نشان میدهد که همه باقیماندهها صفر هستند – یعنی همه موارد مشاهده شده یا نقاط نمونه دقیقاً در خط رگرسیون قرار میگیرند. مقدار ۸۲/۰ به این معنی است که ۸۲ درصد از تغییرات y با x توضیح داده میشود. و ۱۰۰ منهای ۸۲/۰ دیگر (۱۸/۰) درصد از تغییرات توسط متغیرهای دیگری توضیح داده شده است که در مدل رگرسیون لحاظ نشده اند.
گسترش نقاط نمونه در مورد خط رگرسیون با خطای برآورد استاندارد اندازه گیری میشود که به شرح زیر تعریف شده است :
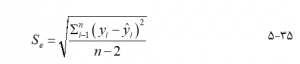
Se ممکن است به عنوان مقدار یک باقی مانده معمولی تفسیر شود. میتوان از آن برای مقایسه نمونههای مختلف با توجه به میزان پراکندگی نقاط مشاهده شده در مورد خط رگرسیون آنها استفاده کرد. همچنین میتواند برای مقایسه توزیعهایی که از خط رگرسیون حداقل مربعات یکسانی برخوردارند استفاده شود.

