سطح روند
درونیابی سطح روند سطح صاف که توسط تابع چند جمله ای تعریف شده است، با مجموعه ای از نقاط نمونه متناسب میکند، سپس از تابع چند جمله ای برای تخمین مقادیر مکانهای نمونه برداری نشده استفاده میکند. به ندرت از نقاط نمونه اصلی عبور میکند. ساده ترین شکل سطح روند، سطح مسطح بدون انحنا است که توسط چند جمله ای خطی یا مرتبه اول تعریف میشود:
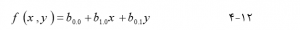
جایی که x و y مختصات هستند bi,j (i,j = 0, 1) ضرایب چند جمله ای هستند وf(x, y) مقدار یک متغیر محیطی در محل (x, y) است. فرض کنید n نقطه نمونه وجود دارد که مقادیر آنها z1, z2, . . ., zn ، و مختصات آنها عبارتند از (x1, y1), (x2, y2), . . ., (xn, yn) ضرایب تابع چند جمله ای را میتوان از نقاط نمونه با به حداقل رساندن موارد زیر تعیین کرد :

این روش حداقل مربعات نامیده میشود که تضمین میکند مجموع انحرافات مجذور مقادیر مشاهده شده در نقاط نمونه از سطح روند حداقل است.
در بسیاری از شرایط سطح مدل شده مطابق با صفحه نیست، بلکه سطح منحنی است. میتوان از چند جمله ای مرتبه دوم (درجه دوم) استفاده کرد که به صورت زیر بیان میشود :
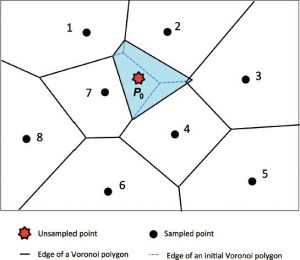
شکل ۴-۲۸ تجمع Voronoi (چند ضلعی سایه دار حاوی نقطه بدون نمونه)
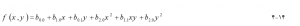
یا چند جمله ای مرتبه سوم (مکعب) میتوان استفاده کرد:
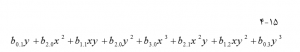
معادله کلی سطح روند عبارت است از :
![]()
که در آن p درجه چند جمله ای است. مطابق شکل نشان داده شده در شکل ۴-۲۹ همانطور که مرتبه چند جمله ای افزایش مییابد، سطحی که برازش میشود تعداد انحناهای فزاینده ای دارد و به تدریج پیچیده تر میشود. اگرچه سفارشات چند جمله ای تا ۱۰ پذیرفته میشود، بی ثباتی عددی در تجزیه و تحلیل اغلب مصنوعاتی را در سطوح روند سفارشات بزرگتر از ۵ ایجاد میکند. این عمدتاً به دلیل تعداد محدود نقاط نمونه در مقایسه با افزایش سریع تعداد ضرایب متصل به چند جملهایهای مرتبه بالا ایجاد میشود.
هنگامی که ضرایب با استفاده از روش حداقل مربعات شرح داده شده در بالا برآورد شدند، تابع چند جمله ای در هر نقطه از ناحیه مورد نظر ارزیابی قرار میگیرد. به دلیل روش برازش حداقل مربعات، هیچ معادله چند جمله ای دیگری با همان ترتیب نمیتواند تقریب بهتری از دادهها ارائه دهد.
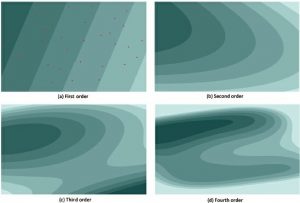
شکل ۴-۲۹ سطوح بارندگی که توسط سطوح روند مرتبههای مختلف در هم آمیخته شده اند: (الف) مرتبه اول، ب) مرتبه دوم، (ج) مرتبه سوم و (د) مرتبه چهارم (با استفاده از مجموعه داده یکسان و علائم مشابه درشکل ۴-۲۷)
درون یابی سطح روند، سطحی صاف ایجاد میکند که نشان دهنده روند جهانی توزیع متغیر محیطی است. بنابراین ، اغلب برای تناسب سطح با نقاط نمونه هنگامی که مقدار متغیر به آرامی در سطح تغییر میکند، مورد استفاده قرار میگیرد. همچنین به عنوان راهی برای حذف ویژگیهای وسیع دادهها قبل از استفاده از سایر روشهای درون یابی استفاده میشود. از چند جمله ایهای مرتبه پایین میتوان برای توصیف فرایندهای فیزیکی متغیر آهسته مانند آلودگی و جهت باد استفاده کرد. با این حال هرچه ترتیب چند جمله ای بیشتر باشد، نسبت دادن معنای فیزیکی به آن دشوارتر است. رایج ترین ترتیب چند جمله ایها ۱ تا ۴ است. علاوه بر این سطوح درون یابی بسیار حساس به نقاط بیرونی (یعنی مقادیر بسیار بالا و پایین) به ویژه در لبهها هستند.
اسپلاین
روش spline مقادیر را در مکانهای نمونه برداری نشده با استفاده از یک تابع ریاضی که انحنای سطح کلی را به حداقل میرساند، تخمین میزند. چندین نوع مختلف از spline وجود دارد. رایج ترین اسپلاینهایی که در GIS برای درون یابی مکانی استفاده میشوند، اسپلاینهای صفحه نازک هستند. چنین نوع اسپلاین سطحی را تولید میکند که دقیقاً از نقاط نمونه عبور میکند و در عین حال از صاف بودن سطح تا حد امکان اطمینان میدهد. شکل کلی تابع spline را میتوان به صورت زیر نوشت :

که در آن x و y مختصات هستند، t(x, y) یک تابع روند است، n تعداد نقاط نمونه است، di فاصله از نقطه نمونه من تا نقطه r(d) (x, y), است. تابع پایه برای بدست آوردن حداقل سطح انحنا و biضرایب طراحی شده است (میتاس و میتاسووآ،۱۹۹۹). برای خطوط با صفحه نازک، یک تابع پایه مجموع مجذورات مشتق دوم سطح گرفته شده در هر نقطه از سطح را به حداقل میرساند (میتاس و میتاسووا ۱۹۹۹). خطوط مختلف با صفحه نازک به اشکال مختلف t(x, y) r(d) هستند. دو شکل متداول از اسپلاینهای صفحه نازک ( اسپلاین منظم و اسپلاین با کشش) وجود دارد.
اسپلین منظم
برای اسپلین معمولی، توابع روند و اساس به شکل زیر است
که در آن τ وزن است، c ثابتی برابر با ۵۷۷۲۱۵/۰ و K0 تابع بسل اصلاح شده است (میتاس و میتاسووا ۱۹۸۸). مقادیر معمول τ عبارتند از ۰، ۰۰۱/۰، ۰۱/۰، ۱/۰ و ۵/۰ هر چه وزن بیشتر باشد، سطح درون یابی صاف تر است. ضرایب bi در معادله ۴-۱۷ و a1, a2 و a3 در معادله ۴-۱۸ توسط سیستم معادلات خطی یافت میشوند :

که در آن zi مقدار در نقطه نمونه یک و n تعداد نقاط نمونه است.
یک مشکل عمده با spline منظم، شیب تند در مناطق با داده ضعیف (جایی که نقاط نمونه بسیار کمی وجود دارد) است که اغلب به عنوان overshoot شناخته میشوند. وزن τ بالاتر از ۰٫۵ تمایل به ایجاد تعداد بیش از حد بالاتر در مناطق با داده ضعیف دارد. این بیش از حد باید اصلاح شود. اسپلاینهای صفحه نازک با کشش برای کاهش مشکل طراحی شده اند.
اسپلاین با تنش
اسپلاین با کشش به کاربران اجازه میدهد تا کشش اعمال شده بر لبههای سطح را کنترل کنند. توابع روند و اساس اسپلین با کشش دارای اشکال زیر است:
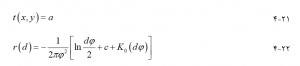
که در آن φ وزن است. هرچه وزن بیشتر باشد، سطح درون یابی درشت تر است و مقادیر تخمینی بیشتر با محدوده دادههای نمونه مطابقت دارند. به عبارت دیگر وزن بیشتر محدوده مقادیر درون یابی یا سفتی سطح را کاهش میدهد. مقادیر معمول φ به صورت ۰ ، ۱ ، ۵ یا ۱۰ تنظیم شده است.
هر دو اسپلین منظم و اسپلین با کشش سطوح صاف و به تدریج متغیر با مقادیر برآوردی ایجاد میکنند که ممکن است خارج از محدوده حداکثر و حداقل مقادیر نقاط نمونه قرار گیرند. برای بحث کامل در مورد این دو روش لطفاً به میتاس و میتاسووا،۱۹۹۸ مراجعه کنید. شکل ۴-۳۰ دو نمونه از سطوح بارندگی را نشان میدهد که با اسپلاین منظم و اسپلین با کشش درون یابی شده اند.

