نسبت باند
کادر ۶-۹ نحوه استفاده از توابع حسابی باند در ArcGIS برای انجام نسبت باند را نشان میدهد.
کادر ۶-۹ نسبت باند در ArcGIS |
کاربردی |
| برای پیروی از این مثال، ArcMap را راه اندازی کنید و تصویر ETM+ image wy00abd.tif را که از نظر رادیومتری تصحیح شده در کادر ۶-۴ ایجاد شده، بارگیری کنید. |
ایجاد نسبتهای باند ساده |
| ۱) در صورت بسته بودن پنجره Image Analysis را باز کنید. |
| ۲) در پنجره Image Analysis : |
| الف) wy00abd.tif را انتخاب کنید. |
| ب) روی دکمه Function Editor کلیک کنید. در گفتگوی Function Template Editor، روی wy00abd.tif راست کلیک کنید، به Insert اشاره کنید و روی Band Arithmetic Function کلیک کنید. |
| ج) در گفتگوی Raster Function Properties ویژگیهای تابع Raster، رستر ورودی به عنوان wy00abd.tif تنظیم میشود User Defined را به عنوان روش انتخاب کنید، عبارت B4/B3 را وارد کنید، سپس روی OK کلیک کنید. |
| د) روی OK کلیک کنید. یک لایه تصویر موقت Func_wy00abd.tif ایجاد و نمایش داده میشود، مانند شکل a6-19 |
| ۳) مرحله ۲ را تکرار کنید تا ترکیبهای دیگری از باندها را برای انجام نسبت باند امتحان کنید. تصاویر نسبت حاصل را برای استخراج اطلاعات مفید تفسیر کنید. |
محاسبه NDVI |
| ۴) در پنجره Image Analysis : |
| الف) wy00abd.tif را انتخاب و برجسته کنید. |
| ب) روی دکمه Function Editor کلیک کنید. در گفتگوی Function Template Editor، روی راست کلیک کنید، به Insert اشاره کنید و روی Band Arithmetic Function کلیک کنید. |
| ۳) در محاوره ویژگیهای تابع Raster، NDVI را به عنوان روش انتخاب کنید و شاخصهای باند ۳ ۴ را وارد کنید (۴ به باند ۴، باند IR نزدیک، ۳ به باند ۳، نوار قرمز در تصویر ترکیبی، و ۴ اشاره دارد و ۳ با یک فاصله از هم جدا میشوند). روی OK کلیک کنید. |
| ۴) روی OK کلیک کنید. یک لایه تصویر موقت ایجاد و نمایش داده میشود، مانند شکل ۶-۲۰ مقادیر NDVI در این تصویر از ۱- تا ۱ متغیر است. عموماً، ابرها، آب و برف ممکن است مقادیر منفی داشته باشند و مقادیر NDVI ماسه، سنگ و خاک برهنه نزدیک به صفر و به طور کلی زیر ۱/۰ است. مقادیر متوسط (۲/۰-۳/۰) ممکن است از درختچهها و علفزارها تولید شود، در حالی که مقادیر بالا (۶/۰-۸/۰) میتواند جنگلها و زمینهای زراعی را نشان دهد. |
تجزیه و تحلیل اجزای اصلی
دادههای تصویری چند طیفی شامل تصاویری از نوارهای طول موج مختلف است که ممکن است مشابه به نظر برسند و به دلیل شباهت پاسخ طیفی ویژگیهای مشاهده شده در آن نوارها، اطلاعات مشابهی را شامل شوند. گفته میشود که چنین تصاویری چند طیفی بسیار مرتبط هستند. همبستگی بین باندی منجر به افزونگی در دادهها میشود. برای کاهش چنین افزونگی از تجزیه و تحلیل اجزای اصلی (PCA) استفاده میشود. این روش ریاضی است که برای شناسایی شباهتها و تفاوتها در یک مجموعه داده و تبدیل مجموعه داده همبسته به مجموعه داده جدید بدون ارتباط ایجاد شده است. این تکنیک که در مجموعه دادههای تصویری چند طیفی با باند n کاربرد دارد، مجموعه داده اصلی تصویر مرتبط را به کمتر از n (اغلب دو یا سه) باند از تصاویر جدید غیر مرتبط، که تصاویر جزء اصلی نامیده میشود، تبدیل میکند. این تصاویر اجزای اصلی میتوانند برای تفسیر و طبقه بندی تصویر به جای دادههای اصلی بدون از دست دادن اطلاعات مورد استفاده قرار گیرند. بنابراین، PCA ممکن است به تولید تصاویری که قابل تفسیرتر از تصاویر اصلی هستند، کمک کند و کارایی محاسباتی تجزیه و تحلیل تصویر بعدی را افزایش دهد، زیرا تعداد نوارها (یا ابعاد) مجموعه دادههای تصویری را که باید تجزیه و تحلیل شوند، کاهش میدهد.
با توجه به مجموعه داده تصویر دو باند، توزیع دو بعدی مقادیر DN از دو باند را میتوان در یک نمودار پراکنده رسم کرد، همانطور که در تصویر شکل ۶-۲۱ نشان داده شده است. اگر همه نقاط روی خط PC1 قرار گیرند، دو باند کاملاً همبسته هستند. در بسیاری از موارد، نقاط در اطراف خط با PC1 به عنوان جهت غالب پراکندگی یا تغییرپذیری پراکنده میشوند. PC1 نشان دهنده جهتی است که در آن بیشترین واریانس وجود دارد و در آن دادهها بیشترین پخش را دارند. جهت اولین جزء اصلی در دادهها است. PC2 خط عمود بر PC1 است و از میانگین توزیع داده میگذرد. این خط جهت دومین جزء اصلی در دادهها را نشان میدهد. اگر تغییر در جهت PC2 شامل کسری کوچک از تنوع کل دادهها باشد، ممکن است بدون حذف اطلاعات زیاد نادیده گرفته شود. برای یافتن تصاویر جزء اصلی، PCA محورهای باند A–Band B را بر روی محورهای PC1-PC2 ترجمه و یا میچرخاند و مقدار DN جدید را برای پیکسل در ردیف i، ستون j بر حسب محورهای۱ PC محاسبه میکند. و۲ PC به شرح زیر محاسبه میشود :
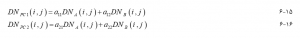
![]()
که در اینجا DNA (i ، j) و DNB (i ، j) مقادیر اصلی پیکسل (i ، j) در تصاویر A و Band B هستند ، DNpc1 (i ، j) مقدار پیکسل تبدیل شده در اولین اصل است تصویر جزء ،( DNpc2 (i ، j مقدار پیکسل تبدیل شده در دومین تصویر جزء اصلی است و (a11 ، a12) و (a21، a22) ضرایبی برای تبدیل هستند که به عنوان بردارهای ویژه یا اجزای اصلی شناخته میشوند. بردارهای ویژه از ماتریس کواریانس مقادیر پیکسل دو باند اصلی محاسبه میشوند.
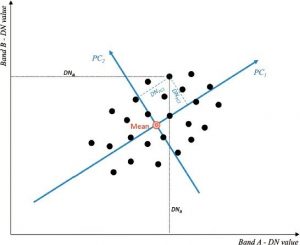
شکل ۶-۲۱ دو جزء اصلی یک تصویر دو باندی
کواریانس بین باند A و B به صورت زیر محاسبه میشود :
که در آن p و q به ترتیب تعداد ردیفها و ستونهای تصویر هستند، میانگین مقدار DN باند A، و میانگین مقدار DN باند B است. این اندازهگیری مقدار پیکسلهای این دو است. باندها از میانگین نسبت به یکدیگر متفاوت هستند. اگر بیش از دو باند در مجموعه داده تصویر وجود داشته باشد، بیش از یک اندازه گیری کوواریانس محاسبه میشود. در واقع، برای یک تصویر باند n، مقادیر کوواریانس متفاوت وجود خواهد داشت. مقادیر کوواریانس بین n باند در یک ماتریس n×n در قالب زیر قرار داده میشود:
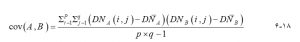
که در اینجا B1 ، B2 و ، Bn به باند ۱ ، باند ۲ و ارجاع داده میشود که در واقع واریانس a است. این ماتریس را ماتریس کوواریانس مینامند. نسبت به قطر اصلی متقارن است. ماتریس دارای n بردار ویژه است که عمود بر هم هستند. هر بردار ویژه دارای ارزش ویژه مرتبط است. بردارهای ویژه با استفاده از تکنیکهای تجزیه جبری خطی یافت میشوند ، که خارج از حوصله این کتاب است. اطلاعات بیشتر در مورد بردارهای ویژه و ارزشهای ویژه به طور کلی و نحوه استخراج آنها را میتوان در هر کتاب جبر خطی استاندارد یافت. به عنوان مثال جدول ۶-۴ ماتریس کوواریانس مشتق شده از wy00abd.tif را فهرست میکند، تصویر شش باندی ETM+ albedo Woori Yallock تصحیح شده رادیومتری است. جدول ۶-۵ بردارهای ویژه، مقادیر ویژه مرتبط و درصد واریانس صحنه محاسبه شده از ماتریس کوواریانس را فهرست میکند.
هنگامی که بردارهای ویژه یافت میشوند، تصاویر جزء اصلی را تولید میشود. به طور کلی مقادیر پیکسل برای تصویر جزء اصلی k از موارد زیر یافت میشود :
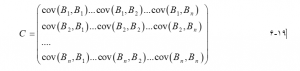
که در آن DNpck(i,j) مقدار DN پیکسل (i,j) در kامین تصویر جزء اصلی است، n تعداد باندها است، DNi(i,j) مقدار پیکسل (i,j) است. در تصویر باند (i = 1, 2, . . ., n) و (،..،..، ..) مشتق شده از ماتریس کوواریانس مقادیر پیکسل تصویر باند n است. شکل ۶-۲۲ شش تصویر مؤلفه اصلی را نشان میدهد که از wy00abd.tif مبتنی بر آن مشتق شده است و در بردارهای ویژه در جدول ۶-۵ ذکر شده است.
تصاویر مؤلفه اصلی بر اساس مقادیر ویژه بردارهای ویژه مرتبط با آنها از بالاترین به کمترین مرتب شده اند. این تصاویر اجزای اصلی را به ترتیب اهمیت میدهد. اولین تصویر جزء اصلی دارای بزرگترین مقدار ویژه است، ۰۰۳۵/۰ در مورد Woori Yallock، همانطور که در جدول ۶-۵ فهرست شده است. این شامل بزرگترین بخش از کل واریانس صحنه، ۶۱/۷۸درصد در مورد Woori Yalllock است. تصویر مؤلفه اصلی دوم حاوی واریانس بسیار کمتری ۹۳/۱۸درصد در مورد Woori Yallock است. سومین تصویر بعدی و قسمت بعدی دارای بخش بیشتری از واریانس صحنه است. تصاویر اجزای اصلی با مقادیر ویژه بالا و درصد زیادی از واریانس صحنه، اطلاعات قابل توجهی در مورد ویژگیهای مشاهده شده ارائه میدهند، در حالی که تصاویر با مقادیر ویژه کوچک و واریانسهای کم، نویز را نشان میدهند و اطلاعات مفید کمی ارائه میدهند. اگر اولین k کوچکتر از n تصاویر مؤلفه اصلی بیشترین واریانس در مجموعه دادههای تصویر چند طیفی را به خود اختصاص دهند، میتوان n باند اصلی دادههای تصویر را کنار گذاشت و تجزیه و تحلیل تصویر بعدی را فقط با استفاده از k تصاویر مؤلفه اصلی انجام داد. در مورد Woori Yallock ، سه تصویر اصلی اصلی حاوی ۳۵/۹۹ درصد از واریانس دادههای اصلی تصویر هستند، به این معنی که آنها تقریباً همه واریانس دادهها را توضیح میدهند. اجزای ۴ ، ۵ و ۶ را میتوان نادیده گرفت زیرا درصد بسیار کمی (۶۵/۰ درصد) از واریانس صحنه را تشکیل میدهند و ناچیز هستند. تصاویر سه جزء تا حد زیادی نویز سیستم را نشان میدهند.
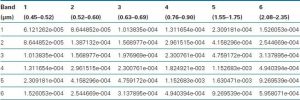
جدول ۶-۴ ماتریس کوواریانس تصویر شش باند ETM+ Woori Yallock
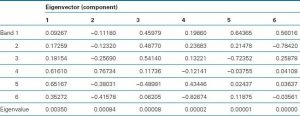
جدول ۶-۵ بردارهای ویژه و مقادیر ویژه محاسبه شده از ماتریس کوواریانس در جدول ۶-۴

شکل ۶-۲۲ تصاویر اصلی جزء Woori Yallock (قسمت مرکزی حوضه آبریز)

