مطالعه ای در مورد دسترسی فضایی پناهگاه اضطراری بر اساس روش حوضه تطبیقی اندازه 2SFCA

خلاصه

برای دستیابی به دسترسی فضایی پناهگاه های اضطراری باید رابطه بین عرضه و تقاضای پناهگاه های اضطراری در دو بعد فضایی و غیرفضایی به طور جامع در نظر گرفته شود. در همین حال، درک رابطه رقابتی میان پناهگاه های اضطراری حیاتی است. با این حال، هنگام استفاده از روش حوضه آبریز شناور دو مرحله ای (۲SFCA) و روش بهبود یافته ۲SFCA هنگام پرداختن به این مسائل، معایبی وجود دارد. این مطالعه روش اندازه حوضه تطبیقی ۲SFCA (A-2SFCA) را برای محاسبه مقادیر دسترسی فضایی پیشنهاد می‌کند که می‌تواند در کنار دو رابطه ذکر شده در بالا کار کند. روش تحلیل روش A-2SFCA دو مرحله دارد. اولا، این روش اندازه حوضه پناهگاه ها را با مشاهده شلوغی آنها و استفاده مکرر از این آمار در زیر مجموعه خدمات تنظیم می کند. در پایان این مرحله، هر حوضه آبریز مشخص می شود. در مرحله دوم، حوضه های آبریز برای محاسبه مقادیر دسترسی مکانی استفاده می شود. این روش برای مطالعه منطقه ای در منطقه شهری تیانجین در چین مورد استفاده قرار گرفت. روش‌های پیشنهادی A-2SFCA و حوضه آبریز شناور دو مرحله‌ای مبتنی بر پوشش ثابت (FC2SFCA) برای اندازه‌گیری و مقایسه مقادیر دسترسی مکانی استفاده می‌شوند. نتایج نشان می دهد که دسترسی فضایی در منطقه شهری تیانجین ناپایدار است. نتیجه دسترسی فضایی به‌دست‌آمده از روش A-2SFCA نسبت به روش FC2SFCA در هنگام تجزیه و تحلیل حوضه‌های منطقی پناهگاه‌های اضطراری معقول‌تر است.

کلید واژه ها:

دسترسی فضایی ؛ A -۲SFCA زیر مجموعه خدمات ; پناهگاه اضطراری ; شلوغی

۱٫ معرفی

پناهگاه های اضطراری امکانات خدمات عمومی مهمی در شهرها هستند که می توانند خدمات ایمنی و زندگی ضروری را در هنگام وقوع فاجعه ارائه دهند [ ۱ ]. با روند شهرنشینی، مردم به طور فزاینده ای در شهرها اسکان می یابند که می تواند منجر به خسارات بیشتر در شهرهای آسیب دیده از بلایای طبیعی شود. از این رو، تامین عادلانه و معقول مکان های امن برای ساکنان بیشتر برجسته شده است.

دسترسی فضایی به درجه راحتی دسترسی به یک مکان نسبت به مکان دیگر اشاره دارد [ ۲ ، ۳ ]. روش‌هایی که معمولاً برای تجزیه و تحلیل دسترسی فضایی استفاده می‌شوند شامل روش‌های حداقل فاصله [ ۴ ]، تحلیل شبکه [ ۵ ]، مدل گرانشی [ ۶ ] و حوضه آبریز شناور دو مرحله‌ای (۲SFCA) [ ۷ ] و همچنین شبیه‌سازی فضایی [ ۸ ] است. ]. از آنجایی که روش ۲SFCA می تواند ویژگی های چند بعدی امکانات خدمات عمومی مانند توزیع فضایی ارائه دهندگان خدمات و تقاضاها و ظرفیت پناهگاه ها را تحلیل کند، به طور گسترده در سناریوهای مختلف استفاده می شود. یک سری مدل با روش ۲SFCA ایجاد شده است [ ۹]. روش ۲SFCA توسط لو و وانگ [ ۱۰ ] پیشنهاد شد که به طور جامع رابطه کمیت فضایی بین طرف عرضه و تقاضای خدمات را در نظر گرفتند. با این حال، روش اصلی ۲SFCA در رابطه با سه جنبه متمایز برای سازگاری با محیط‌های پیچیده و دنیای واقعی، که شامل فروپاشی فاصله [ ۱۱ ]، اندازه مناطق حوضه [ ۱۲ ]، و رقابت عرضه یا تقاضای خدمات است، توسعه داده شد. امکانات [ ۱۳ ]. روش ۲SFCA معکوس [ ۱۴ ] برای اندازه گیری ازدحام امکانات عرضه پیشنهاد شد. روش حوضه آبریز شناور دو مرحله ای مبتنی بر پوشش ثابت (FC2SFCA) [ ۱۵] با استفاده از حوضه آبریز تامین کنندگان خدمات در مراحل یک و دو در سال ۲۰۲۰ توسعه داده شد. روش اصلی ۲SFCA و نسخه های اصلاح شده آن برای تجزیه و تحلیل دسترسی فضایی امکانات عمومی مانند پارک ها استفاده شده است [ ۱۶ ، ۱۷ ، ۱۸ ] ، فضاهای سبز [ ۱۹ ]، بیمارستان ها [ ۲۰ ، ۲۱ ، ۲۲ ]، مدارس [ ۲۳ ]، پناهگاه های اورژانس [ ۲۴ ]، ایستگاه های آتش نشانی [ ۲۵ ]، فرصت های شغلی [ ۲۶ ] و بانک ها [ ۲۷ ]. با این حال، روش ۲SFCA و نسخه های اصلاح شده آن هنوز هنگام تلاش برای حل و فصل سه جنبه متمایز، ضعف دارند.

توابع فروپاشی فاصله مختلفی وجود دارد: توزیع گاوسی [ ۲۵ ]، تراکم هسته [ ۲۸ ]، و تابع ترکیبی [ ۲۹ ]. با این حال، یکپارچه سازی عملکرد فروپاشی برای موقعیت های مختلف دشوار است. در مورد اندازه حوضه، لو یک روش حوضه آبریز شناور دو مرحله ای متغیر (V-2SFCA) با خلاصه کردن عوامل تقاضا یا عرضه برای محاسبه شعاع حوضه پیشنهاد کرد [ ۳۰ ]. مک گریل با بررسی تجربه و تراکم جمعیت شعاع خدمات پزشکی را به پنج دسته تقسیم کرد [ ۱۲ ]. تائو شعاع خدمات یک آژانس بازنشستگی را بر اساس ظرفیت خدمات آن ارزیابی کرد [ ۳۱]. این الگوریتم ها تعامل داخلی بین عوامل عرضه و تقاضا را در دو بعد کمیت و توزیع فضایی در محاسبه شعاع جستجو در نظر نمی گیرند که معمولاً منجر به خطاهای محاسباتی در دسترسی مکانی می شود [ ۳۲ ]. اندازه حوضه تامین کنندگان خدمات تحت تاثیر عوامل متعددی مانند کمیت و موقعیت مکانی عرضه و تقاضا و رقابت داخلی بین طرف عرضه و تقاضا قرار دارد. در حالی که هر منبع خدماتی اندازه حوضه خود را دارد، دستیابی به اندازه حوضه مناسب برای جستجوی تامین کنندگان خدمات در مرحله دوم روش ۲SFCA دشوار است. در روش حوضه آبریز شناور دو مرحله ای معکوس (i2SFCA)، همین مشکل به دلیل شعاع های مختلف سرویس رخ می دهد.

در حال حاضر، محققان متعددی در حال مطالعه دسترسی فضایی پناهگاه های اضطراری با روش ۲SFCA و انواع آن هستند. برای مثال، ژو دسترسی مکانی یک پناهگاه اضطراری در چانگچون را با روش متغیر ۲SFCA محاسبه کرد [ ۲۴ ]. ژو دسترسی فضایی پناهگاه های اضطراری در پکن را با استفاده از روش افزایش یافته حوزه آبریز شناور دو مرحله ای (E2SFCA) مطالعه کرد [ ۳۳]. با این حال، رقابت پذیری هم در پناهگاه های اضطراری و هم در مناطق سرشماری در این مطالعات نادیده گرفته شده است. تفاوت قابل توجهی بین پناهگاه های اضطراری و سایر امکانات عمومی وجود دارد. تقاضای شهروندان برای پناهگاه های اضطراری در پی وقوع یک فاجعه بالا و رقابتی است. شهروندان قطعا از پناهگاه های اضطراری در دسترس خود استفاده کامل خواهند کرد. به طور کلی، زمانی که چندین پناهگاه خدمات خود را ارائه می دهند، تمایل دارند یک پناهگاه نسبتاً کمتر شلوغ را انتخاب کنند. با این حال، روش ۲SFCA کمتر به آن عوامل توجه دارد. بنابراین، هنگام تصمیم گیری در مورد اندازه حوضه پناهگاه های اضطراری، روش سنتی ۲SFCA سفت و سخت است و دسترسی فضایی پناهگاه های اضطراری نادرست است.

در ادبیات پیشنهاد شده است که شعاع خدمات و رابطه رقابتی پناهگاه‌های اضطراری تعاملی هستند. جوهر رقابت میان پناهگاه های اضطراری، انتخاب پناهگاه توسط افراد تخلیه شده است. برای مهاجران، عواملی که بر انتخاب سرپناه تأثیر می گذارد، فاصله و کیفیت خدمات ارائه شده برای نیازهای آنها است. این مقاله شلوغی را به عنوان یک پارامتر مهم برای بازتاب کیفیت خدمات ارائه شده در نظر می گیرد. از دیدگاه تخلیه‌شدگان، آنها تمایل دارند پناهگاهی با شلوغی کمتر را در یک منطقه فضایی نزدیک انتخاب کنند، که باعث ایجاد رقابت بین پناهگاه‌های اضطراری می‌شود. از دیدگاه ارائه دهنده خدمات، اندازه منطقه خدماتی یک پناهگاه اضطراری نشان دهنده رقابت بین آنها است. به عبارت دیگر، زمانی که ازدحام در یک پناهگاه کمتر از میانگین شلوغی پناهگاه های اطراف آن باشد، پناهگاه جذاب و رقابتی است. در این صورت، افراد از فاصله دورتر جذب پناهگاه می شوند و در نتیجه شعاع خدمات آن را گسترش می دهند که وضعیت رقابت پذیری آن را بهبود می بخشد. در این مقاله مفهوم زیر مجموعه خدمات تعریف شده است. در ابتدا، ما روشی را برای محاسبه اندازه حوضه پناهگاه‌های اضطراری با استفاده از زیرمجموعه‌های خدمات مربوط به توزیع جمعیت و پناهگاه‌های اضطراری، وزن پناهگاه‌های اضطراری و تأثیر آن‌ها بر اطرافیانشان پیشنهاد می‌کنیم. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. پس پناهگاه جذاب و رقابتی است. در این صورت، افراد از فاصله دورتر جذب پناهگاه می شوند و در نتیجه شعاع خدمات آن را گسترش می دهند که وضعیت رقابت پذیری آن را بهبود می بخشد. در این مقاله مفهوم زیر مجموعه خدمات تعریف شده است. در ابتدا، ما روشی را برای محاسبه اندازه حوضه پناهگاه‌های اضطراری با استفاده از زیرمجموعه‌های خدمات مربوط به توزیع جمعیت و پناهگاه‌های اضطراری، وزن پناهگاه‌های اضطراری و تأثیر آن‌ها بر اطرافیانشان پیشنهاد می‌کنیم. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. پس پناهگاه جذاب و رقابتی است. در این صورت، افراد از فاصله دورتر جذب پناهگاه می شوند و در نتیجه شعاع خدمات آن را گسترش می دهند که وضعیت رقابت پذیری آن را بهبود می بخشد. در این مقاله مفهوم زیر مجموعه خدمات تعریف شده است. در ابتدا، ما روشی را برای محاسبه اندازه حوضه پناهگاه‌های اضطراری با استفاده از زیرمجموعه‌های خدمات مربوط به توزیع جمعیت و پناهگاه‌های اضطراری، وزن پناهگاه‌های اضطراری و تأثیر آن‌ها بر اطرافیانشان پیشنهاد می‌کنیم. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. که وضعیت رقابت پذیری آن را بهبود می بخشد. در این مقاله مفهوم زیر مجموعه خدمات تعریف شده است. در ابتدا، ما روشی را برای محاسبه اندازه حوضه پناهگاه‌های اضطراری با استفاده از زیرمجموعه‌های خدمات مربوط به توزیع جمعیت و پناهگاه‌های اضطراری، وزن پناهگاه‌های اضطراری و تأثیر آن‌ها بر اطرافیانشان پیشنهاد می‌کنیم. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. که وضعیت رقابت پذیری آن را بهبود می بخشد. در این مقاله مفهوم زیر مجموعه خدمات تعریف شده است. در ابتدا، ما روشی را برای محاسبه اندازه حوضه پناهگاه‌های اضطراری با استفاده از زیرمجموعه‌های خدمات مربوط به توزیع جمعیت و پناهگاه‌های اضطراری، وزن پناهگاه‌های اضطراری و تأثیر آن‌ها بر اطرافیانشان پیشنهاد می‌کنیم. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. و تاثیر آنها بر اطرافیانشان. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است. و تاثیر آنها بر اطرافیانشان. سپس با استفاده از روش FC2SFCA، دسترسی فضایی پناهگاه های اضطراری را محاسبه می کنیم. این روش به اندازه های تطبیقی حوضه ۲SFCA (A-2SFCA) معروف است.

بقیه این مقاله به شرح زیر سازماندهی شده است: بخش ۲ منطقه و داده های مورد مطالعه را توصیف می کند. بخش ۳ به روش پیشنهادی می پردازد. بخش ۴ نتایج تجربی را تجزیه و تحلیل می کند. بخش ۵ بحث را ارائه می کند. و در نهایت، بخش ۶ نتیجه گیری را ارائه می کند.

۲٫ منطقه مطالعه و داده ها

تیانجین یکی از چهار شهرداری چین است و مرکز حمل و نقل در شمال چین است. منطقه مورد مطالعه این مطالعه منطقه مرکزی شهر تیانجین است که از شش ناحیه تشکیل شده است ( شکل ۱ ). مساحت این منطقه ۱۹۴٫۲۲ کیلومتر مربع است. کل جمعیت تا پایان سال ۲۰۲۰ تقریباً ۴ میلیون (۴۰۵۷۲۰۰) بود. به منظور اصلاح داده های جمعیت، این مطالعه داده های توزیع جمعیت WorldPop را با استفاده از داده های سرشماری هفتم جمعیت تنظیم کرد. میانگین تراکم جمعیت در منطقه شهری ۲۰۸۸۸ نفر در هر کیلومتر مربع است. منطقه هپینگ دارای بیشترین تراکم جمعیت است که به ۳۵۵۵۲ نفر در هر کیلومتر مربع می رسد. ولسوالی هکسی با ۱۶۹۲۶ نفر در هر کیلومتر مربع کمترین تراکم جمعیت را در مقایسه با پنج ولسوالی دیگر دارد.

تا سال ۲۰۲۰، ۶۸۲ پناهگاه اضطراری در مرکز شهر تیانجین ( شکل ۱ ) وجود داشت که شامل پارک ها، فضاهای سبز و زمین های بازی مدارس می شد. تا به امروز، دو نوع پناهگاه اضطراری وجود دارد: پناهگاه های مرکزی و موقت با شعاع خدمات مربوطه به ترتیب ۱۵۰۰ و ۵۰۰ متر.

در این مطالعه از چهار نوع داده استفاده شد. داده های پناهگاه اضطراری ( شکل ۱ ) از دفتر مدیریت اضطراری تیانجین ( http://yjgl.tj.gov.cn ، در تاریخ ۱ ژوئن ۲۰۲۲) به دست آمده است. داده های WorldPop از برنامه تحقیقاتی WorldPop ( https://www.worldpop.org ، دسترسی به ۶ ژوئن ۲۰۲۲) به دست آمد، و داده های WorldPop مورد استفاده در این آزمایش، داده های توزیع جمعیت برای سال ۲۰۲۰ با وضوح ۱۰۰ × بود. ۱۰۰ متر ^مربع . داده‌های WorldPop نیز همراه با داده‌های سرشماری هفتم ( http://stats.tj.gov.cn ، دسترسی به ۶ ژوئن ۲۰۲۲) از پیش پردازش شدند. میز ۱برخی از داده های اساسی مانند سرشماری هفتم، داده های پناهگاه اضطراری، تراکم جمعیت و مساحت سرپناه به ازای هر نفر را ارائه می دهد. می توان مشاهده کرد که مناطق سرپناه برای هر نفر در ناحیه هبی و هدونگ نسبتاً کوچک است.

۳٫ روش ها

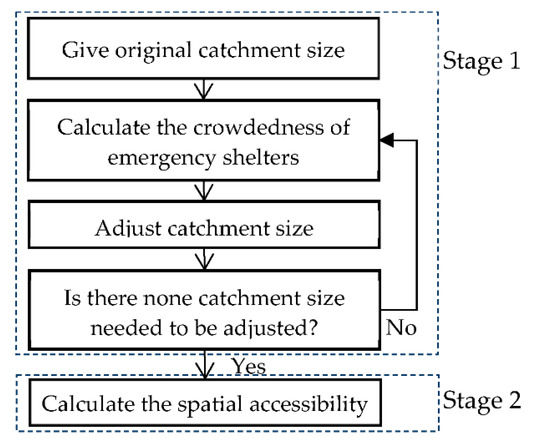
روش A-2SFCA دو مرحله دارد. مرحله اول محاسبه اندازه حوضه پناهگاه اضطراری است. مرحله دوم تعیین دسترسی فضایی است.

همپوشانی های متعددی در حوضه های آبریز پناهگاه ها وجود دارد. مفهوم زیر مجموعه خدمات در محاسبه شعاع حوضه های آبریز پناهگاه های اضطراری برای تسهیل محاسبات تحلیلی استفاده می شود. زیرمجموعه خدمات شامل یک سرپناه اصلی و تعدادی پناهگاه برده است. هنگامی که حوضه یک پناهگاه اضطراری (به نام پناهگاه اصلی زیرمجموعه خدمات) نیاز به تنظیم داشته باشد، به راحتی می توان مشاهده کرد که حوضه آن با چندین حوضه پناهگاه های اضطراری دیگر همپوشانی دارد (به نام پناهگاه های برده این زیر مجموعه خدماتی) . پناهگاه اصلی موضوع مطالعه در زیر مجموعه خدمات است. پناهگاه های برده دارای حوضه هایی هستند که با حوضه آبریز پناهگاه اصلی تلاقی می کنند.

در مرحله اول، شعاع حوضه های آبریز پناهگاه های اضطراری با ارزش طراحی ارائه می شود و ابتدا میزان ازدحام آنها محاسبه می شود. در زیرمجموعه خدماتی هر پناهگاه اضطراری، زمانی که میزان ازدحام در پناهگاه اصلی کمتر از میانگین شلوغی در پناهگاه های برده باشد، شعاع حوضه آبریز پناهگاه اصلی افزایش می یابد. در این حالت، پناهگاه اصلی جذاب‌تر از پناهگاه‌های برده در زیرمجموعه خدماتی است که سطح شلوغی آن به طور قابل توجهی کمتر است. هنگامی که شعاع حوضه یک پناهگاه اصلی افزایش می یابد، نشان داده می شود که پناهگاه در زیر مجموعه خدمات خود رقابتی می شود. شعاع حوضه آبریز پناهگاه اصلی تنها ۱۰ درصد از شعاع اصلی خود در یک زمان افزایش می یابد. در محاسبات، حداکثر شعاع حوضه آبریز هر پناهگاه ۱۵۰۰ متر است. این روش به صورت دوره ای برای تنظیم شعاع حوضه آبریز هر پناهگاه استفاده می شود تا زمانی که دیگر شعاع پناهگاهی برای تنظیم وجود نداشته باشد. در نهایت تمام حوضه های آبریز پناهگاه ها مشخص می شود. در مرحله ۲، دسترسی فضایی پناهگاه های اضطراری بر اساس روش FC2SFCA با استفاده از حوضه آبریز نهایی در مرحله ۱ محاسبه می شود.

فرآیند محاسبه در شکل ۲ ارائه شده است . مرحله ۱ مرحله کلیدی روش A-2SFCA است. در مرحله ۱، حوضه هر پناهگاه اضطراری تعیین می شود. در معادلات ارائه شده در این قسمت واحد هم ظرفیت سرپناه اضطراری و هم تراکت سرشماری یک نفر است. واحد فاصله متر است.

۳٫۱٫ با استفاده از روش i2SFCA، شلوغی را محاسبه کنید

در مرحله ۱ روش A-2SFCA، ازدحام در پناهگاه های اضطراری پارامتر کلیدی برای تنظیم حوضه است. روش i2SFCA [ ۱۴ ] برای محاسبه شلوغی پناهگاه های اضطراری استفاده می شود. روش i2SFCA شامل دو مرحله است: مرحله ۱ شدت رقابت را برای هر بخش سرشماری محاسبه می کند. مرحله ۲ خواسته های هر پناهگاه اضطراری را خلاصه می کند. تابع گاوسی [ ۲۶ ] برای اندازه گیری زوال زمان سفر استفاده می شود. با این حال، روش i2SFCA مورد استفاده در این مطالعه در دو مکان تنظیم شد: ابتدا حوضه ثابت معرفی شد و سپس هر حوضه در یک پناهگاه اضطراری منحصر به فرد بود.

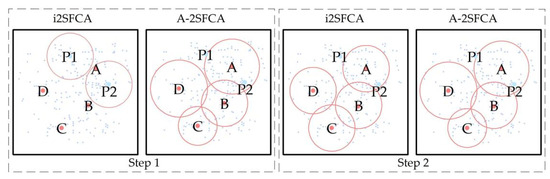
این دو تفاوت در شکل ۳ ارائه شده است. چهار پناهگاه اضطراری (یعنی A، B، C و D) و دو راه سرشماری (یعنی P1 و P2) وجود دارد. فاصله آستانه سفر روش i2SFCA در مراحل ۱ و ۲ برابر است. آنها در روش A-2SFCA متفاوت هستند. در هر دو مرحله روش i2SFCA از مراکز مختلف حوضه آبریز استفاده شد. روش A-2SFCA از حوضه های آبریز تاسیسات تامین در مراحل ۱ و ۲ استفاده کرد.

مراحل دقیق برای محاسبه شلوغی در زیر ذکر شده است:

(۱): در ابتدا، مقدار حوضه آبریز با اندازه حوضه طراحی می شود.
(۲): برای هر مکان سرشماری i ، تمام پناهگاه های اضطراری j را که حوضه های آبریز i را پوشش داده اند ، جستجو کنید و نسبت تقاضا به عرضه Q _j را محاسبه کنید. کاهش فاصله توسط تابع گاوسی کاهش می یابد.
(۳): برای هر پناهگاه اضطراری j ، تمام سرشماری‌های خدماتی i را در محدوده خدمات آن جستجو کنید و مجموع نسبت‌های تقاضا به عرضه ضرب در وزن گاوسی را محاسبه کنید. مجموع این شلوغی پناهگاه j است.

سیj=∑j∈تیمنجی(دمنj،د۰)سj=∑j∈تیمنپمن∑j∈{دمنj≤دj}جی(دمنj،د۰)بj

(۱)

جایی که i نقطه تقاضا است. j نقطه عرضه است. C _j مقدار درجه تراکم نقطه عرضه است. Q _j نسبت جمعیت نقطه تقاضا تحت پوشش خدمات نقطه عرضه j به ظرفیت خدمات است. T _i مجموعه ای از نقاط عرضه است که خدماتی را به نقطه تقاضا ارائه می دهند . B _j ظرفیت سرویس ارائه دهنده خدمات j است . P _i مقیاس تقاضای نقطه تقاضا i است . d _ij فاصله بین تقاضا استi و نقاط عرضه j ; d _j شعاع سرویس نقطه عرضه j است . و جی(دمنj،د۰)تابع گاوسی است که زوال فاصله را در نظر می گیرد. واحدهای P _i و B _j افراد هستند. واحدهای d _ij , d _۰ و d _j متر هستند. محاسبه تابع گاوسی در رابطه (۲) ارائه شده است.

جی(دمنj،د۰)={ه-(۱۲)×(دمنjد۰)-ه-(۱۲)۱-ه-(۱۲) دمنj≤د۰ ۰ دمنj>د۰

(۲)

در معادله (۲)، d _ij نشان دهنده فاصله بین نقطه تقاضا i و عرضه j است. d _۰ حداکثر فاصله ای است که ارائه دهنده خدمات می تواند خدمات خود را ارائه دهد. واحدهای d _ij و d _۰ متر هستند.

۳٫۲٫ روش تنظیم اندازه حوضه آبریز

به منظور توصیف واضح تر فرآیند تنظیم اندازه حوضه پناهگاه های اضطراری، از زیر مجموعه خدمات استفاده شد. اندازه حوضه هر پناهگاه اضطراری با محاسبه شلوغی پناهگاه های اصلی و برده مربوطه در زیر مجموعه خدمات تنظیم شد. به عنوان مثال، چهار پناهگاه اضطراری در شکل ۴ الف ارائه شده است. حوضه آبریز مربوطه آنها نواحی مدور است. طبق تعریف زیرمجموعه خدمات، زیرمجموعه خدماتی پناهگاه A شامل دو پناهگاه A و B است که با مجموعه _A = { A , B } مشخص می شود، زیرا حوضه های آبریز پناهگاه های Aو B قطع می کنند. پناهگاه A سرپناه اصلی زیر مجموعه است. پناهگاه برده پناهگاه A را نیز می توان به عنوان یک مجموعه مشاهده کرد که به عنوان Set _{slave_A} = { B } نشان داده می شود. به طور مشابه، زیرمجموعه سرویس پناهگاه B را می توان به صورت مجموعه _B = { A , B , C , D } ثبت کرد. پناهگاه B در این زیرمجموعه سرپناه اصلی است و او پناهگاه های A ، C و D در این زیر مجموعه پناهگاه های برده هستند. پناهگاه های برده پناهگاه B به عنوان ثبت شده استSlave_B = { A, C , D } را تنظیم _{کنید .}زیرمجموعه سرویس و پناهگاه های برده پناهگاه C را می توان به صورت Set _B = { B , C , D } و Set _{slave_B} = { B , D } ثبت کرد. نمادهای مجموعه _D = { B , C , D } و Set _{slave_D} = { B , C } زیر مجموعه خدمات و پناهگاه های برده پناهگاه اضطراری هستندد .

هنگام محاسبه شلوغی پناهگاه ها برای اولین بار در مرحله ۱، فاصله آستانه سفر پناهگاه های اضطراری با توجه به شعاع طراحی شده آنها محاسبه شد. همانطور که در بالا ذکر شد دو نوع شعاع طراحی وجود دارد. پس از به دست آوردن شلوغی هر پناهگاه با استفاده از رابطه (۱)، هم شلوغی سرپناه اصلی و هم مقادیر میانگین شلوغی پناهگاه های برده در زیر مجموعه خدمات به دست آمد. از طریق مقایسه رابطه بین شلوغی سرپناه اضطراری اصلی و شلوغی پناهگاه‌های برده در زیر مجموعه خدمات، می‌توان فاصله آستانه سفر پناهگاه اصلی را تنظیم کرد. قوانین تنظیم برای مسافت آستانه به شرح زیر ذکر شده است:

(۱): حداکثر فاصله آستانه کمتر از ۱۵۰۰ متر است.
(۲): برای پناهگاه i ، زیرمجموعه خدمات آن Set _i است. با مقایسه شلوغی پناهگاه اضطراری i و میانگین شلوغی پناهگاه های برده در مجموعه _i ، می توانیم فاصله آستانه جدید پناهگاه i را با استفاده از رابطه (۳) محاسبه کنیم:

دمن={دمن۰ (دمن۰=۱۵۰۰ متر or ∑j∈اسهتیسلآvه_منسیj(n-1)×سیمن≤۱ or |∑j∈اسهتیسلآvه_منسیj(n-1)×سیمن-۱|<0.1)دمن۰×∑j∈اسهتیسلآvه_منسیj(n-1)×سیمن (|∑j∈اسهتیسلآvه_منسیj(n-1)×سیمن-۱|≥۰٫۱ آnد دمن<1500 متر) ۱۵۰۰ (دمن۰×∑j∈اسهتیسلآvه_منسیj(n-1)×سیمن ≥۱۵۰۰ متر)

(۳)

که در آن d _i آستانه جدید مسافت سفر پناهگاه i است، d _i0 مسافت آستانه قدیمی پناهگاه i است، n تعداد پناهگاه ها در زیرمجموعه سرویس پناهگاه i است، Set _{slave_i} مجموعه پناهگاه های برده از i است. ، C _i شلوغی پناهگاه اضطراری i است و C _j درجه ازدحام پناهگاه j در زیرمجموعه خدماتی پناهگاه i است. واحدهای d _i0 و d_من متر هستم

همانطور که در رابطه (۳) نشان داده شده است، شرایط متعددی وجود دارد که باید در نظر گرفته شوند ( شکل ۴ ). برای مثال، چهار پناهگاه اضطراری در شکل ۴ الف ارائه شده است. شعاع پناهگاه اضطراری D ۱۵۰۰ متر است، بنابراین حوضه آبریز پناهگاه اضطراری D نیازی به تغییر ندارد. در مورد پناهگاه اضطراری B ، زیر مجموعه خدمات آن دارای چهار عنصر است : A ، B ، C و D. میانگین شلوغی پناهگاه های بردگان B C _{B_avg} است. با پیروی از قوانین ارائه شده در رابطه (۳)، اگر C _B ده درصد کمتر از C باشد_{B_avg} و d _B0 کمتر از ۱۵۰۰ متر است، سپس شعاع آن باید تنظیم شود. دو شرط باید در نظر گرفته شود. اگر شعاع تنظیم شده d _B کمتر از ۱۵۰۰ متر باشد، آنگاه d _B شعاع جدید حوضه خواهد بود. همانطور که در شکل ۴ ب نشان داده شده است، دایره قرمز و نقطه چین حوضه بعدی پناهگاه اضطراری B است. اگر شعاع تنظیم شده d _B برابر یا بزرگتر از ۱۵۰۰ متر باشد، مقدار d _B برابر با ۱۵۰۰ متر خواهد بود. در شکل ۴ نشان داده شده استج که دایره نقطه‌دار آبی با استفاده از رابطه (۳) محاسبه می‌شود، اما شعاع آن بزرگ‌تر از ۱۵۰۰ متر است، یعنی شعاع نهایی آن دایره نقطه‌دار قرمز خواهد بود که شعاع آن ۱۵۰۰ متر است.

با استفاده از این روش، نیازی به تغییر حوضه آبریز پناهگاه اضطراری نخواهد بود تا زمانی که هر پناهگاه اضطراری شلوغی مشابه پناهگاه های اضطراری اطراف خود داشته باشد و یا فاصله آستانه سفر آن ۱۵۰۰ متر باشد. علاوه بر این، در پایان مرحله ۱، حوضه نهایی هر پناهگاه اضطراری تعیین خواهد شد.

۳٫۳٫ محاسبه دسترسی فضایی

دسترس‌پذیری از نظریه مکان کلاسیک [ ۶ ] نشات می‌گیرد که درک متفاوتی در سناریوهای کاربردی مختلف دارد. برای سناریوهای دسترسی، مانند مراقبت‌های بهداشتی، بازنشستگی، و فضاهای سبز، زاویه تحقیق بیشتر به سمت سطح ترافیک و فاصله است. بعد ذهنی نیز در مطالعه تأثیر فاصله بر دسترسی در نظر گرفته شده است [ ۳۴]. این مقاله دسترسی به یک پناهگاه اضطراری را به عنوان سهولتی که با آن افراد تخلیه شده از یک منطقه آسیب دیده از فاجعه می توانند با پای پیاده از محل خود به پناهگاه برسند و نیازهای تخلیه خود را برآورده کنند، تعریف می کند. این تعریف شامل سه ویژگی است: اولاً، تقاضا برای خدمات تخلیه یک موج کوتاه مدت است. ثانیا، نحوه حمل و نقل پیاده است، که تعیین کننده مسافت های محدودی است که می تواند توسط مکان های تخلیه اشغال شود. و ثالثاً، حجم بالای تقاضاها یک اثر رقابتی و ازدحام بر تقاضا برای خدمات تخلیه با کیفیت بالا و رقابت بین سایت‌های تخلیه ایجاد می‌کند. این عوامل منجر به مطالعه دسترسی به پناهگاه هایی می شود که دارای ویژگی های مشترک و منحصر به فرد در ارتباط با دسترسی به سایر خدمات عمومی هستند.

دسترسی فضایی پناهگاه های اضطراری با استفاده از روش FC2SFCA محاسبه می شود که نسخه بهبود یافته روش ۲SFCA است. تابع واپاشی فاصله آن یک تابع گاوسی است. در این روش از حوضه آبریز مبتنی بر پوشش ثابت استفاده می شود. نسبت عرضه به تقاضا برای هر پناهگاه اضطراری در رابطه (۴) محاسبه می شود. دسترسی مکانی هر پناهگاه در رابطه (۵) محاسبه می شود:

(۱): برای هر سرپناه اضطراری j ، تمام مسیرهای سرشماری i در آستانه مسافت سفر d _j پناهگاه اضطراری جستجو می شود. سپس، نسبت عرضه به تقاضا Rj _را می توان با توجه به رابطه (۴) محاسبه کرد. تعداد تقاضای پناهگاه های اضطراری استفاده شده j با تابع گاوسی وزن می شود.
(۲): برای هر بخش سرشماری i ، همه پناهگاه‌های اضطراری که می‌توانند خدماتی را به سرشماری i ارائه دهند جستجو می‌شوند و همه نسبت‌های عرضه-تقاضا Rj _که برای دستیابی به دسترسی فضایی A j استفاده می‌شود ، _خلاصه می‌شوند :

آرj=اسj∑j∈{دمنj≤دj}جی(دمنj،د۰)Dک

(۴)

آj=∑j∈تیمنجی(دمنj،د۰)آرj

(۵)

که در آن Aj دسترسی فضایی سرشماری _i است، _Rj نسبت عرضه به تقاضای پناهگاه اضطراری j است، T i زیرمجموعه پناهگاه اضطراری است _که خدماتی را به مسیر سرشماری ارائه می‌کند ، _S j ظرفیت است . از پناهگاه اضطراری j ، D _k عدد تقاضای راه سرشماری k است، d _ij فاصله بین پناهگاه اضطراری j و مسیر سرشماری i ، d _{j است.}آستانه نهایی مسافت سفر است و جی(دمنj،د۰)تابع گاوسی است. واحد S _j و D _k افراد است.

۴٫ نتایج و تجزیه و تحلیل

برای مقایسه A-2SFCA پیشنهادی با روش‌های FC2SFCA، دسترسی فضایی یک پناهگاه اضطراری محاسبه‌شده با استفاده از روش FC2SFCA اندازه‌گیری و تجزیه و تحلیل شد.

۴٫۱٫ فرآیند شناخت حوضه های آبریز مناسب پناهگاه ها

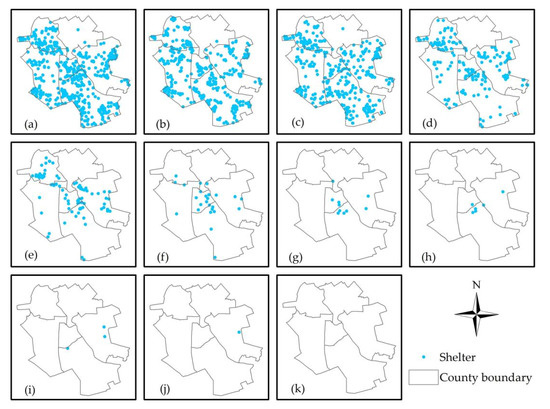
محاسبه انجام شده در مرحله ۱ از روش A-2SFCA برای تنظیم حوضه بر اساس شلوغی پناهگاه های اضطراری استفاده شد. ۱۱ بار محاسبه شلوغی و ۱۰ بار تغییر شعاع حوضه های آبریز در پناهگاه های اضطراری در مرحله ۱ برای به دست آوردن شعاع نهایی پناهگاه اضطراری تیانجین با استفاده از معادلات (۱) – (۳) انجام شد. این فرآیند در شکل ۵ ارائه شده است . شکل ۵ پناهگاه های اضطراری را نشان می دهد که فاصله آستانه سفر آنها هر بار باید تنظیم شود. از شکل ۵ a-k می توان مشاهده کرد که تعداد پناهگاه های اضطراری به تدریج کاهش می یابد. کاهش تعداد پناهگاه ها در شکل ۵ آشکارتر استه. این بدان معنی است که بیشتر تنظیمات مربوط به اندازه حوضه پناهگاه ها در طول پنج تلاش اول انجام می شود. متعاقباً، تنظیم پناهگاه ها به تنظیم دقیق چند پناهگاه تبدیل می شود.

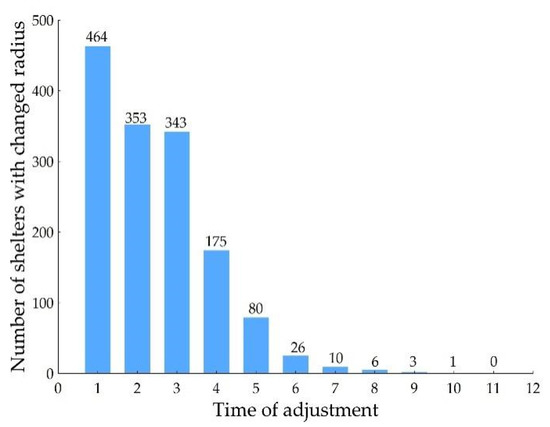
شکل ۶ تغییر کمی ۱۰ برابری تنظیم حوضه آبریز پناهگاه را نشان می دهد. تعداد پناهگاه ها در اولین تنظیم بیشترین میزان را دارد. تقریباً دو سوم از حوزه های آبریز پناهگاه ها تعدیل شد. تعداد پناهگاه هایی که نیاز به تعدیل داشتند در دفعات دوم و سوم به حدود نصف کاهش یافت. تعداد آن پناهگاه ها از بار چهارم تا پایان به سرعت کاهش یافت. با شروع دور هفتم، تعداد تعدیل حوضه های آبریز پناهگاه ها کمتر از ۱۰ بود. محاسبه صفر در زمان یازدهم نشان می دهد که اندازه حوضه اضطراری وجود ندارد که نیاز به تنظیم داشته باشد، که این نیز نشان دهنده پایان مرحله ۱ روش A-2SFCA.

۴٫۲٫ تحلیل دسترسی فضایی پناهگاه های اضطراری

شکل ۷ دسترسی فضایی پناهگاه های اضطراری در منطقه شهری تیانجین را با استفاده از روش A-2SFCA نشان می دهد. به طور کلی، دسترسی فضایی به غرب و جنوب منطقه شهری تیانجین بهتر است. بیشتر منطقه هبی کمترین ارزش دسترسی مکانی را دارد زیرا فقط دو پناهگاه اضطراری دارد و این قسمت به رنگ آبی نشان داده شده است. ولسوالی های مرکزی و شرقی نسبتاً پایین تر هستند که به دلیل سرانه پایین پناهگاه در این دو منطقه است (همانطور که در جدول ۱ نشان داده شده است ). سرانه مساحت سرپناه در ناحیه هدونگ ۰٫۵۱۵ متر مربع به ازای هر ^نفر است، در حالی که در ناحیه نانکای ۰٫۷۷۷ متر مربع است ^./ شخص با وجود سرانه بالای سرپناه در منطقه هپینگ، دسترسی در مناطق همسایه هبی، هدونگ و نانکای نیز کاهش یافته است. در میان شش منطقه در شهر، Hexi، Hongqiao، و بیشتر Nankai دارای بهترین ارزش دسترسی فضایی هستند.

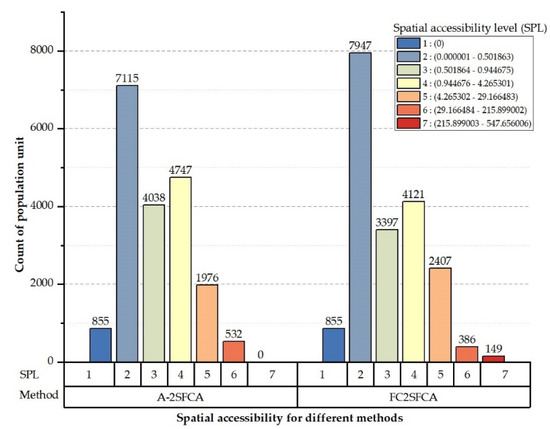
به منظور تجزیه و تحلیل اثر روش مورد استفاده در این مقاله، از روش دیگری برای اندازه گیری دسترسی به پناهگاه های اضطراری در منطقه شهری تیانجین استفاده کردیم که روش FC2SFCA بود. علاوه بر این، نتیجه روش FC2SFCA در شکل ۸ ارائه شده است . تفاوت این دو روش در فاصله آستانه سفر پناهگاه های اضطراری است. در روش A-2SFCA، فاصله با تنظیم ۱۰ برابری محاسبه شد. با این حال، فاصله آستانه استفاده شده در روش FC2SFCA، مسافت طراحی شده بود. از نتایج محاسباتی این دو روش می توان مشاهده کرد که دسترسی فضایی ناشی از شعاع های مختلف سرویس متفاوت است.

۴٫۳٫ مقایسه روش های A-2SFCA و FC2SFCA

روند توزیع دسترسی فضایی پناهگاه ها در منطقه شهری تیانجین محاسبه شده با دو روش سازگار بود. می توان مشاهده کرد که منطقه با قابلیت دسترسی بالا محاسبه شده با روش A-2SFCA ( شکل ۷ ) به طور قابل توجهی بیشتر از مساحت ارائه شده در شکل ۸ است. این نشان می دهد که افراد بیشتری در محاسبه روش A-2SFCA شانس بیشتری برای استفاده از پناهگاه های اضطراری دارند. حداکثر مقدار دسترسی فضایی ارائه شده در شکل ۸ بیشتر از آن در شکل ۷ است. در شکل ۹ مشاهده می شود که نتایج به دست آمده با استفاده از روش A-2SFCA مقادیر شدید و حداقلی کمتری را ارائه می دهند.

۴٫۴٫ مقایسه تغییرات در محاسبه استفاده از روش A-2SFCA

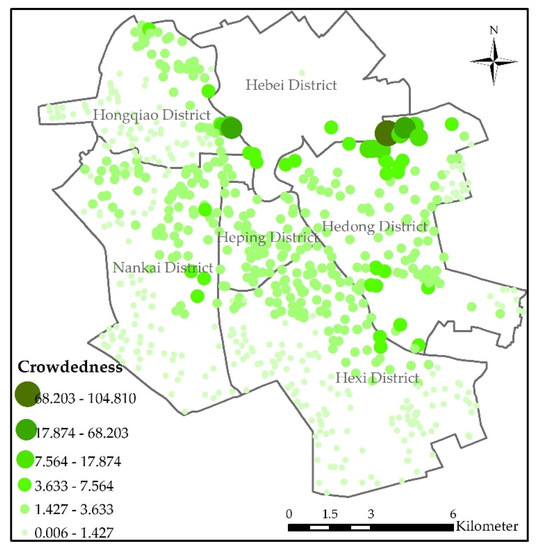
شلوغی شاخص کلیدی مورد استفاده در مرحله اول بود. این شاخص توزیع جمعیت، ظرفیت سرپناه و توزیع سرپناه را ترکیب کرد. این نشانگر برای تنظیم شعاع خدمات هر پناهگاه استفاده شد. شکل ۱۰ شلوغی نهایی استفاده از روش A-2SFCA را نشان می دهد. شلوغی پناهگاه های اضطراری با استفاده از فاصله سفر آستانه طراحی شده اولیه به عنوان اندازه حوضه طراحی شده محاسبه می شود ( شکل ۱۱ ). شلوغی از دو روش به طور کلی در توزیع فضایی مشابه است. با این حال، تعداد پناهگاه هایی با درجه ازدحام بیشتر از ۷٫۵۶۴ در شکل ۱۰ بسیار کمتر از شکل ۱۱ است.. شلوغی پناهگاه های اضطراری با موقعیت های جغرافیایی مشابه نیز در شکل ۱۰ نسبتا مشابه است، اما این پدیده در شکل ۱۱ وجود ندارد . نتایج در شکل ۱۰ معقول تر است، زیرا مردم تمایل دارند پناهگاهی با شلوغی کمتر را بیشتر انتخاب کنند. در بیشتر مناطق، شلوغی پناهگاه های اضطراری در شکل ۱۰ کمتر از شکل ۱۱ است. با این حال، شلوغی پناهگاه های اضطراری در شکل ۱۰ بیشتر از شکل ۱۱ در منطقه ای است که منطقه هبی به منطقه هدونگ و منطقه نانکای متصل می شود.

مشاهده می شود که ظرفیت کلی خدمات پناهگاه های اضطراری در اکثر مناطق منطقه شهری تیانجین نسبتاً خوب است. با این حال، منطقه هبی نیاز به تقویت ساخت پناهگاه های اضطراری دارد.

۵٫ بحث

این مقاله ابتدا مفهوم زیرمجموعه خدمات را معرفی کرد که دیدگاه جدیدی برای تجزیه و تحلیل ظرفیت خدمات ارائه دهندگان خدمات عمومی در یک منطقه محلی ارائه می دهد. مفهوم زیرمجموعه خدمات نشان دهنده رابطه بین ارائه دهندگان خدمات در یک منطقه محلی است، از جمله رابطه حمایتی یا رقابتی متقابل بین ارائه خدمات داخلی آنها. ثانیاً، عناصر موجود در زیرمجموعه خدمات برای سهولت محاسبه متمایز می شوند. یک رابطه master و slave بین عناصر درون زیر مجموعه وجود دارد. آنها را به ترتیب عناصر سرویس master و slave می نامند. این رابطه ارباب و برده برای تنظیم اندازه شعاع ناحیه خدماتی پناهگاه اصلی در ارتباط با داده های توزیع جمعیت استفاده می شود. در این صفحه، عناصر سرویس برده مکان هایی از سرپناه بودند که در آن یک همپوشانی فضایی با منطقه خدماتی عنصر سرویس اصلی وجود داشت. با این حال، در زمینه های دیگر، این مفهوم از یک زیرمجموعه خدمات نیز می تواند معرفی شود، و عضویت و رابطه master-slave مفهوم زیر مجموعه سرویس با سناریوی کاربردی واقعی سازگار است. به عنوان مثال، در مطالعه این مثال، اعضای زیرمجموعه خدمات را نیز می توان با چنین مجموعه ای تطبیق داد، که در آن عناصر برده این مجموعه با ناحیه ای تلاقی می کنند که در مرکز پناهگاه اصلی قرار دارد و به سمت خارج در شعاع امتداد می یابد. ۱۵۰۰ متر یا مقدار فاصله متفاوت. این وضعیت در جایی به وجود می‌آید که اگرچه مناطق خدماتی دو پناهگاه با هم تلاقی نمی‌کنند، اما با این وجود رابطه حمایتی متقابلی دارند. ممکن است واقع بینانه تر باشد که محدوده زیرمجموعه سرویس را به این شکل تعریف کنیم.

از سوی دیگر، یک حوضه آبریز ثابت برای محاسبه شلوغی پناهگاه ها وارد شد. شعاع خدمات یک پناهگاه تحت تأثیر عوامل متعددی قرار گرفت که منجر به ایجاد شعاع خدماتی غیریکنواخت شد. اگر روش سنتی i2SFCA دنبال شود، استفاده از همان شعاع در محاسبه دو مرحله ای برای جستجوی محاسبه نادرست است.

در نهایت، شلوغی، به عنوان یک پارامتر تنظیمی برای شعاع خدمات پناهگاه، می تواند ترکیبی از جنبه ها، از جمله ظرفیت پناهگاه، توزیع فضایی آن، و توزیع تراکم جمعیت را منعکس کند. شلوغی عناصر در یک زیرمجموعه خدمات می تواند منعکس کننده حمایت یا رقابت مکان های پناهگاه نزدیک باشد. چنین پارامتر انتزاعی، که می تواند روابط پیچیده بین ویژگی ها را در بعد بالاتر منعکس کند، شاید برای تجزیه و تحلیل شعاع خدمات پناهگاه منطقی تر باشد.

در مقایسه با روش‌های قبلی، روش پیشنهادی در این مقاله از نظر محاسباتی بسیار فشرده‌تر بود، به‌ویژه زمانی که دانه‌بندی فضایی داده‌های توزیع جمعیت کم بود و تعداد محاسبات به طور قابل‌توجهی افزایش یافت.

۶٫ نتیجه گیری

دسترسی فضایی به پناهگاه های اضطراری تحت تأثیر عوامل مختلفی از جمله تعداد و توزیع فضایی متقاضیان و تامین کنندگان آنها و رقابت بین تامین کنندگان خدمات قرار گرفت. یک روش A-2SFCA توسعه یافته برای محاسبه دسترسی فضایی پیشنهاد شد. در این روش، مفهوم یک سرویس زیرمجموعه تعریف شد که برای تجزیه و تحلیل تأثیر متقابل عرضه نزدیک جغرافیایی و تنظیم اندازه حوضه پناهگاه‌های اضطراری با شلوغی استفاده شد. علاوه بر این، هنگام محاسبه میزان تراکم یا دسترسی فضایی، هنگام جستجوی عرضه یا تقاضای خدمات، از همان حوضه های آبریز استفاده می شود که به آن حوضه ثابت نیز می گویند. این روش می تواند برای اندازه گیری دسترسی فضایی سناریوهای خدماتی دیگر مانند خدمات بهداشتی، فضای سبز،

پناهگاه های اضطراری در منطقه شهری تیانجین، چین، به عنوان نمونه ای برای آزمایش روش پیشنهادی در این مقاله استفاده شد. هنگام مقایسه روش پیشنهادی A-2SFCA و روش ۲SFCA، مشاهده کردیم که توزیع دسترسی پناهگاه‌های اضطراری در منطقه شهری تیانجین ناهموار بود. دسترسی در مناطق جنوبی و غربی منطقه شهری تیانجین به طور قابل توجهی بهتر از منطقه شمال شرقی بود. این نشان می دهد که ساخت پناهگاه های اضطراری در قسمت شمال شرقی شهر تیانجین کندتر از سایر مناطق است. در عین حال، به دلیل تراکم جمعیت بیشتر در منطقه مرکز شهر، میزان ازدحام پناهگاه های اضطراری نیز بیشتر است.

روش A-2SFCA می تواند از مناطق حوضه آبریز معقول تری برای دسترسی به مقادیر دسترسی مکانی استفاده کند. با این حال، این روش همچنان محدودیت هایی دارد. اول از همه، این روش برای شرایطی که تامین کنندگان خدمات نسبتاً متراکم هستند، نسبتاً مناسب است. هنگامی که ارائه دهندگان خدمات پراکنده هستند و حوضه های آبریز آنها با یکدیگر همپوشانی ندارند، الگوریتم در این مقاله کار نمی کند. در آینده، روش دسترسی فضایی پناهگاه های اضطراری باید بیشتر مورد مطالعه قرار گیرد.

منابع

سو، اچ. چن، دبلیو. وانگ، زی. ارزیابی شلوغی پناهگاه های اضطراری شهری بر اساس مدل گرانشی بهبودیافته. IOP Conf. سر. محیط زمین. علمی ۲۰۲۰ , ۵۰۲ , ۰۱۲۰۴۶٫ [ Google Scholar ] [ CrossRef ]
جوزف، AE; Bantock، PR اندازه گیری قابلیت دسترسی فیزیکی به پزشکان عمومی در مناطق روستایی: روش و مطالعه موردی. Soc. علمی پزشکی ۱۹۸۲ ، ۱۶ ، ۸۵-۹۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
خان، AA یک رویکرد یکپارچه برای اندازه گیری دسترسی فضایی بالقوه به خدمات مراقبت های بهداشتی. اجتماعی-اقتصادی طرح. علمی ۱۹۹۲ ، ۲۶ ، ۲۷۵-۲۸۷٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
Ingram, DR مفهوم دسترسی: جستجوی یک فرم عملیاتی. Reg. گل میخ. ۱۹۷۱ ، ۵ ، ۱۰۱-۱۰۷٫ [ Google Scholar ] [ CrossRef ]
Salas-Olmedo، MH; گارسیا، پی. گوتیرز، جی. ارزیابی بهبود زیرساخت دسترسی و حمل و نقل: نقش مرزها و مقاومت چندجانبه. ترانسپ Res. بخش A سیاست سیاست. ۲۰۱۵ ، ۸۲ ، ۱۱۰-۱۲۹٫ [ Google Scholar ] [ CrossRef ]
Hansen، WG چگونه دسترسی به استفاده از زمین شکل می دهد. مربا. Inst. طرح. ۱۹۵۹ ، ۲۵ ، ۷۳-۷۶٫ [ Google Scholar ] [ CrossRef ]
رادکه، جی. Mu، L. تجزیه فضایی، مدل سازی و نقشه برداری مناطق خدماتی برای پیش بینی دسترسی به برنامه های اجتماعی. ان GIS ۲۰۰۰ ، ۶ ، ۱۰۵-۱۱۲٫ [ Google Scholar ] [ CrossRef ]
آره.؛ چن، ی. خو، Q. ژانگ، اس. یونگ، EHK؛ چان، EHW تعبیه برابری فضایی در یک منطقه سریع شهری: پیاده‌روی و قرار گرفتن در معرض آلودگی هوا. Cities ۲۰۲۲ , ۱۳۱ , ۱۰۳۹۴۲٫ [ Google Scholar ] [ CrossRef ]
چن، ایکس. Jia, P. A Analysis Comparative of Accessibility Measures by the Two-step Floating Catchment Area (2SFCA). بین المللی جی. جئوگر. Inf. علمی ۲۰۱۹ ، ۳۳ ، ۱۷۳۹–۱۷۵۸٫ [ Google Scholar ] [ CrossRef ]
لو، دبلیو. Wang, F. Measures of Spatial Accessibility to Health Health in a GIS Environment: Synthesis and a Case Study در منطقه شیکاگو. محیط زیست برنامه ریزی کنید. ب برنامه ریزی دس ۲۰۰۳ ، ۳۰ ، ۸۶۵-۸۸۴٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
وانگ، اف. اندازه‌گیری، بهینه‌سازی و تأثیر دسترسی به مراقبت‌های بهداشتی: بررسی روش‌شناختی. ان دانشیار صبح. Geogr. ۲۰۱۲ ، ۱۰۲ ، ۱۱۰۴-۱۱۱۲٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
مک گریل، ام آر؛ هامفریس، JS اندازه گیری دسترسی فضایی به مراقبت های اولیه در مناطق روستایی: بهبود اثربخشی روش حوضه آبریز شناور دو مرحله ای. Appl. Geogr. ۲۰۰۹ ، ۲۹ ، ۵۳۳-۵۴۱٫ [ Google Scholar ] [ CrossRef ]
وان، ن. زو، بی. استرنبرگ، تی. روش حوضه آبریز شناور سه مرحله ای برای تحلیل دسترسی فضایی به خدمات بهداشتی. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۲ ، ۲۶ ، ۱۰۷۳-۱۰۸۹٫ [ Google Scholar ] [ CrossRef ]
Wang, F. روش حوضه آبریز شناور معکوس دو مرحله ای برای اندازه گیری شلوغی تأسیسات. پروفسور Geogr. ۲۰۱۸ ، ۷۰ ، ۲۵۱-۲۶۰٫ [ Google Scholar ] [ CrossRef ]
مائو، ک. چن، ی. وو، جی. هوانگ، جی. یانگ، دبلیو. Xia، Z. اندازه گیری دسترسی فضایی خدمات آتش نشانی شهری با استفاده از حوادث آتش سوزی تاریخی در نانجینگ، چین. بین المللی J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۵۸۵٫ [ Google Scholar ] [ CrossRef ]
دیائو، ی. هو، دبلیو. او، ب. تجزیه و تحلیل تأثیر مقیاس پارک بر ارزش ویژه پارک شهری بر اساس ۲۱ سناریو افزایشی در منطقه مرکزی شهری چونگ کینگ، چین. Adv. حفظ کنید. سیستم ۲۰۲۱ ، ۵ ، ۲۱۰۰۱۷۱٫ [ Google Scholar ] [ CrossRef ]
وانگ، اف. وانگ، ک. اندازه‌گیری دسترسی فضایی به فضاهای تفریحی بوم‌شناختی در منطقه دلتای رودخانه مروارید: یک روش بهبود یافته حوزه آبریز شناور دو مرحله‌ای. جی. اسپات. علمی ۲۰۱۸ ، ۶۳ ، ۲۷۹-۲۹۵٫ [ Google Scholar ] [ CrossRef ]
ژانگ، دبلیو. لی، اس. گائو، ی. لیو، دبلیو. جیائو، ی. زنگ، سی. گائو، ال. وانگ، تی. تغییرات سفر و دسترسی عادلانه به پارک‌های شهری در دوره پس از همه‌گیری کووید-۱۹: شواهدی از ووهان، چین. جی. محیط زیست. مدیریت ۲۰۲۲ , ۳۰۴ , ۱۱۴۲۱۷٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
ژانگ، اس. آره.؛ چن، ی. جینگ، ی. Zeng، F. دسترسی به فضای سبز پارک در ووهان، چین: پیامدها برای برابری فضایی در دوران پس از COVID-19. بین المللی جی. محیط زیست. Res. بهداشت عمومی ۲۰۲۲ ، ۱۹ ، ۵۴۴۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
پان، جی. وی، دی. سیلر، BC; آهنگ، سی. وانگ، ایکس. یک شاخص مراقبت های بهداشتی بیمار خارجی (EPHI) برای شبیه سازی تمایلات فضایی در رفتار جستجوی مراقبت های بهداشتی. جلو. بهداشت عمومی ۲۰۲۲ , ۱۰ , ۷۸۶۴۶۷٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
شائو، ی. Luo, W. مدل منطقه حوضه شناور دو مرحله ای تنظیم شده عرضه-تقاضا (SDA-2SFCA) برای اندازه گیری دسترسی فضایی به مراقبت های بهداشتی. Soc. علمی پزشکی ۲۰۲۲ ، ۲۹۶ ، ۱۱۴۷۲۷٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
کار، ا. وان، ن. کووا، تی جی; وانگ، اچ. Lizotte، SL با استفاده از GIS برای درک تأثیر طوفان هاروی بر دسترسی فضایی به مراقبت های اولیه. ریسک مقعدی ۲۰۲۲ ، ۴۲ ، ۸۹۶-۹۱۱٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
لطفا، ع. تائو، آر. Su, Y. ارزیابی دسترسی پیاده‌روی مدارس دولتی کوک برای استفاده به عنوان فضای باز. بین المللی J. Urban Sci. ۲۰۲۲ ، ۱-۱۸٫ [ Google Scholar ] [ CrossRef ]
زو، ایکس. تانگ، ز. لیو، ایکس. لی، ایکس. لین، پی. وانگ، تی. روش بهبود یافته حوضه آبریز شناور دو مرحله ای برای ارزیابی دسترسی فضایی به پناهگاه های اضطراری شهری. پایداری ۲۰۱۸ ، ۱۰ ، ۲۱۸۰٫ [ Google Scholar ] [ CrossRef ]
شیا، ز. لی، اچ. چن، ی. Yu, W. یکپارچه سازی ابعاد فضایی و غیر فضایی برای اندازه گیری دسترسی به خدمات آتش نشانی شهری. بین المللی J. Geo-Inf. ۲۰۱۹ ، ۸ ، ۱۳۸٫ [ Google Scholar ] [ CrossRef ]
تائو، ز. ژو، جی. لین، ایکس. چائو، اچ. لی، جی. بررسی تأثیرات حمل و نقل عمومی بر دسترسی به شغل در شنژن، چین: یک رویکرد چند وجهی. خط‌مشی استفاده از زمین ۲۰۲۰ ، ۹۹ ، ۱۰۵۰۲۵٫ [ Google Scholar ] [ CrossRef ]
لنگفورد، ام. هیگز، جی. جونز، اس. درک تغییرات فضایی در دسترسی به بانک ها با استفاده از تکنیک های حوزه آبریز شناور متغیر. Appl. تف کردن مقعدی ۲۰۲۱ ، ۱۴ ، ۴۴۹-۴۷۲٫ [ Google Scholar ] [ CrossRef ]
دای، دی. نابرابری های نژادی/قومی و اجتماعی-اقتصادی در دسترسی به فضای سبز شهری: کجا باید مداخله کرد؟ Landsc. طرح شهری. ۲۰۱۱ ، ۱۰۲ ، ۲۳۴-۲۴۴٫ [ Google Scholar ] [ CrossRef ]
گونگ، اس. گائو، ی. ژانگ، اف. مو، ال. کانگ، سی. لیو، ی. ارزیابی نابرابری منابع مراقبت های بهداشتی در پکن، چین بر اساس اندازه گیری دسترسی فضایی بهبود یافته. ترانس. GIS ۲۰۲۱ ، ۲۵ ، ۱۵۰۴-۱۵۲۱٫ [ Google Scholar ] [ CrossRef ]
لو، دبلیو. Whippo، T. اندازه‌های متغیر حوضه برای روش حوضه شناور دو مرحله‌ای (۲SFCA). Health Place ۲۰۱۲ ، ۱۸ ، ۷۸۹-۷۹۵٫ [ Google Scholar ] [ CrossRef ]
تائو، ZL؛ چنگ، ی. دای، TQ اندازه گیری دسترسی فضایی به مراکز مراقبت مسکونی در پکن. Prog. Geogr. ۲۰۱۴ ، ۳۳ ، ۶۱۶-۶۲۴٫ [ Google Scholar ] [ CrossRef ]
پارک، جی. گلدبرگ، دویچه وله مروری بر مطالعات اخیر دسترسی فضایی که از اطلاعات مکانی پیشرفته سود برده است: حمل و نقل چندوجهی و تفکیک مکانی و زمانی. بین المللی J. Geo-Inf. ۲۰۲۱ ، ۱۰ ، ۵۳۲٫ [ Google Scholar ] [ CrossRef ]
ژو، ا. چن، ال. زو، اچ. چن، اس. منطقی بودن توزیع فضایی برای سرپناه اضطراری شهری در ناحیه مرکزی پکن در مقیاس جامعه. J. Sefety Environ. ۲۰۲۱ ، ۲۱ ، ۱۶۶۲-۱۶۶۹٫ [ Google Scholar ] [ CrossRef ]
وانگ، اف. تانگ، کیو. برنامه ریزی به سمت دسترسی برابر به خدمات: رویکرد برنامه نویسی درجه دوم. محیط زیست برنامه ریزی کنید. ب برنامه ریزی دس ۲۰۱۳ ، ۴۰ ، ۱۹۵-۲۱۲٫ [ Google Scholar ] [ CrossRef ]

شکل ۱٫ توزیع فضایی تراکم جمعیت و پناهگاه های اضطراری در منطقه شهری تیانجین، چین.

شکل ۲٫ نمودار جریان روش پیشنهادی اندازه حوضه متغیر ۲SFCA (A-2SFCA).

شکل ۳٫ مقایسه روش های i2SFCA و A-2SFCA برای تولید حوضه آبریز.

شکل ۴٫ تنظیم حوضه آبریز پناهگاه B بر اساس شلوغی آن و میانگین شلوغی پناهگاه های برده آن. ( الف ) مناطق حوضه آبریز قبل از تنظیم؛ ( ب ) تنظیم حوضه آبریز پناهگاه B بر اساس ردیف دوم معادله (۳). ( ج ) تنظیم حوضه آبریز پناهگاه B بر اساس ردیف های سوم معادله ( ۳ ).

شکل ۵٫ نقشه توزیع پناهگاه های اضطراری که اندازه های حوضه باید برای آنها تنظیم شود. ( الف ) توزیع پناهگاههایی که اندازه حوضه آنها برای اولین بار تنظیم شده است. ب ) توزیع پناهگاههایی که اندازه حوضه آنها برای بار دوم تنظیم شده است. ( ج ) توزیع پناهگاههایی که اندازه حوضه آنها برای سومین بار تنظیم شده است. ( د ) توزیع پناهگاههایی که اندازه حوضه آنها برای بار چهارم تنظیم شده است. ث ) توزیع پناهگاههایی که اندازه حوضه آنها برای پنجمین بار تنظیم شده است. ( و) توزیع پناهگاههایی که اندازه حوضه آنها برای ششمین بار تعدیل شده است. ( گ) توزیع پناهگاه هایی که اندازه حوضه آنها برای هفتمین بار تعدیل می شود. ح ) توزیع پناهگاههایی که اندازه حوضه آنها برای بار هشتم تنظیم شده است. ( i ) توزیع پناهگاههایی که اندازه حوضه آنها برای نهمین بار تنظیم شده است. ی ) توزیع پناهگاهی که اندازه حوضه آن برای دهمین بار تنظیم شده است . ( k ) اندازه حوضه هیچ پناهگاهی وجود ندارد که نیاز به تنظیم در بار یازدهم داشته باشد.

شکل ۶٫ هیستوگرام شماره تنظیم پناهگاه های اضطراری.

شکل ۷٫ توزیع دسترسی فضایی با روش A-2SFCA محاسبه شده است.

شکل ۸٫ توزیع دسترسی فضایی با روش FC2SFCA محاسبه شده است.

شکل ۹٫ مقایسه دسترسی فضایی با دو روش محاسبه شده است.

شکل ۱۰٫ توزیع شلوغی در پایان روش مرحله ۱ A-2SFCA.

شکل ۱۱٫ توزیع شلوغی در ابتدای روش مرحله ۱ A-2SFCA.

ونوس نصیرفام

3 فوریه 2023

مقالات

مطالعه ای در مورد دسترسی فضایی پناهگاه اضطراری بر اساس روش حوضه تطبیقی اندازه ۲SFCA

خلاصه

کلید واژه ها:

۱٫ معرفی

۲٫ منطقه مطالعه و داده ها

۳٫ روش ها