شناسایی هم‌خوشه‌ها با روندهای منسجم در سری‌های زمانی مرجع جغرافیایی

چندین مطالعه روی تجزیه و تحلیل هم‌خوشه‌بندی داده‌های مکانی-زمانی کار کرده‌اند. با این حال، بیشتر آنها به دنبال هم‌خوشه‌هایی با مقادیر مشابه می‌گردند و قادر به شناسایی هم‌خوشه‌هایی با روندهای منسجم نیستند، که به عنوان تمایلات مشابه در ویژگی‌ها تعریف می‌شود. در این مطالعه، ما الگوریتم هم‌خوشه‌بندی برگمن را با حداقل باقیمانده مجموع مجذور (BCC_MSSR) ارائه می‌کنیم که از باقیمانده برای کمی کردن روندهای منسجم استفاده می‌کند و شناسایی هم‌خوشه‌ها با روندهای منسجم در سری‌های زمانی جغرافیایی ارجاع‌شده را امکان‌پذیر می‌سازد. دمای ماهانه هلندی بیش از ۲۰ سال در ۲۸ ایستگاه به عنوان مجموعه داده مطالعه موردی استفاده شد. ایستگاه-خوشه، ماه-خوشه و هم-خوشه در نتایج BCC_MSSR نشان داده شد و با هم-خوشه هایی با مقادیر مشابه مقایسه شد. در مجموع ۱۱۲ خوشه مشترک با تغییرات دمایی مختلف در نتایج شناسایی شد، و ۱۶ هم خوشه نماینده نشان داده شد، و هفت نوع روند دمایی منسجم خلاصه شد: (۱) افزایش. (۲) کاهش؛ (۳) ابتدا افزایش و سپس کاهش. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. و (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. و ۱۶ هم خوشه نماینده نشان داده شد، و هفت نوع از روند دمای منسجم خلاصه شد: (۱) افزایش. (۲) کاهش؛ (۳) ابتدا افزایش و سپس کاهش. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. و (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. و ۱۶ هم خوشه نماینده نشان داده شد، و هفت نوع از روند دمای منسجم خلاصه شد: (۱) افزایش. (۲) کاهش؛ (۳) ابتدا افزایش و سپس کاهش. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. و (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. و (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. و (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق و دوره‌های زمانی خاص بررسی کرده است. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب به هدف وظایف خاص بستگی دارد.

کلید واژه ها:

هم‌خوشه‌بندی ؛ روندهای منسجم ؛ هلند ؛ سری دما ؛ داده کاوی

۱٫ مقدمه

به لطف پیشرفت رصد زمین و سیستم های شبیه سازی مدل، مقادیر بی سابقه ای از داده های مکانی-زمانی با وضوح های مختلف انباشته شده است [ ۱ ، ۲ ]. از یک طرف، این حجم عظیم داده فرصت هایی را برای بررسی الگوهای پیچیده و دانش برای کمک به تصمیم گیری فراهم می کند [ ۳ ]. از سوی دیگر، چگونگی استخراج الگوها از این داده ها به یک مسئله چالش برانگیز تبدیل می شود [ ۴ ]. به عنوان یکی از مهم‌ترین وظایف داده‌کاوی، روش‌های خوشه‌بندی عناصر داده را با شناسایی موارد مشابه و جداسازی موارد غیرمشابه در خوشه‌ها گروه‌بندی می‌کنند، بنابراین به استخراج الگوهای اساسی در داده‌ها کمک می‌کنند [ ۵ ، ۶ ، ۷ ]].

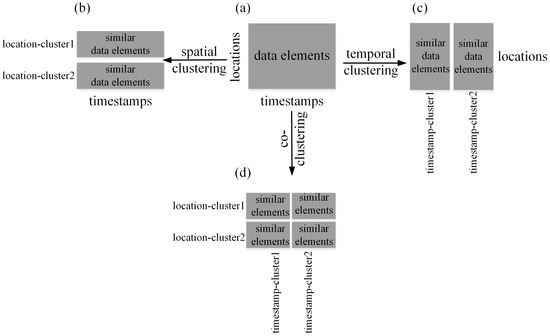
مطالعات زیادی در مورد تجزیه و تحلیل الگوها در داده های مکانی- زمانی با استفاده از روش های خوشه بندی انجام شده است [ ۸ ]. اکثر مطالعات از روش‌های خوشه‌بندی سنتی استفاده می‌کنند، که روش‌های خوشه‌بندی یک‌طرفه را نیز نامیده‌اند، که الگوهای مکانی یا زمانی را در داده‌ها تحلیل می‌کنند و بنابراین خوشه‌بندی مکانی یا خوشه‌بندی زمانی نامیده می‌شوند. به طور خاص، روش‌های خوشه‌بندی فضایی داده‌ها را در امتداد بعد فضایی تجزیه و تحلیل می‌کنند و عناصر داده مشابه را در امتداد تمام مهرهای زمانی به خوشه‌هایی از مکان‌ها تقسیم می‌کنند ( شکل ۱ a,b). به عنوان مثال، آندرینکو و همکاران. [ ۹ ] از نقشه خودسازماندهی (SOM) به عنوان یک روش خوشه‌بندی یک طرفه برای شناسایی خوشه‌های فضایی توزیع‌های زمانی مشابه در داده‌های ترافیک شهر استفاده کرد. هاگناور و هلبیخ [ ۱۰] SOM مکانی-زمانی سلسله مراتبی (HSTSOM) را پیشنهاد کرد، که الگوهای مکانی و زمانی را به طور جداگانه در لایه‌ها برای جستجوی خوشه‌ها در داده‌های اجتماعی-اقتصادی تحلیل می‌کرد. لیو و همکاران [ ۱۱ ] از روش خوشه‌بندی k-means برای شناسایی خوشه‌های فضایی حالت‌ها با سری‌های زمانی مشابه منحنی‌های همبستگی مکانی برای بررسی تأثیر سیاست‌ها بر انتقال COVID-19 استفاده کرد. روش‌های خوشه‌بندی زمانی داده‌ها را در امتداد بعد زمانی تجزیه و تحلیل می‌کنند و عناصر داده مشابه را در امتداد همه مکان‌ها به خوشه‌هایی از مهرهای زمانی گروه‌بندی می‌کنند ( شکل ۱ a,c). به عنوان مثال، آهاس و همکاران. [ ۱۲ ] سال‌های با ریتم مشابه فعالیت‌های انسانی را با تجزیه و تحلیل خوشه‌بندی برای تمایز مناظر شهری و روستایی گروه‌بندی کرد. وو و همکاران [ ۱۳] سال‌هایی را با تغییرات دمایی مشابه در تمام ایستگاه‌های هلند شناسایی کرد تا رفتار متغیر زمانی در داده‌های آب و هوای هلند را بررسی کند.

اخیراً تجزیه و تحلیل هم‌خوشه‌بندی داده‌های مکانی-زمانی توجه محققان در زمینه جغرافیایی را به خود جلب کرده است. برخلاف خوشه‌بندی یک طرفه، روش‌های هم‌خوشه‌بندی ( شکل ۱ a,d) داده‌ها را از هر دو جنبه مکانی و زمانی به طور همزمان تجزیه و تحلیل می‌کنند و عناصر داده مشابه را در امتداد هر دو بعد به خوشه‌هایی از مکان‌ها و مهرهای زمانی تقسیم می‌کنند [ ۸ ]. در نتیجه، آنها قادر به کشف الگوهای مکانی و زمانی در داده ها به طور همزمان هستند. وو و همکاران [ ۱۴ ] از روش هم‌خوشه‌بندی برای تحلیل الگوهای دما در امتداد ابعاد مکانی و زمانی در سری دمای هلندی استفاده کرد. وو و همکاران [ ۱۵ ] و وو و همکاران. [ ۱۶] از روش هم‌خوشه‌بندی برای بررسی الگوهای تمایزات مکانی و زمانی در فنولوژی بلندمدت بهاره در اروپا و چین استفاده کرد. الله و همکاران [ ۱۷ ] خوشه‌های بیماری بالقوه فضا-زمان را در سری‌های سالانه و ماهانه مالاریا در پاکستان با استفاده از تجزیه و تحلیل هم‌خوشه‌بندی شناسایی کرد. آندریو و همکاران [ ۱۸ ] از روش هم‌خوشه‌بندی برای شناسایی خوشه‌های مکانی-زمانی شرایط مطلوب برای ظهور و نگهداری نیل غربی در یونان استفاده کرد. لیو و همکاران [ ۱۹ ] روش هم‌خوشه‌بندی را برای داده‌های تاکسی منهتن برای کشف الگوهای تحرک در ابعاد مکانی و زمانی اعمال کرد.

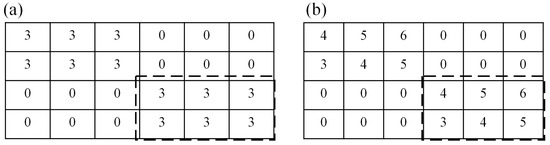
حتی اگر آن روش‌های هم‌خوشه‌بندی فوق داده‌ها را از هر دو جنبه مکانی و زمانی تجزیه و تحلیل کرده‌اند، آنها فقط قادر به شناسایی هم‌خوشه‌هایی با مقادیر مشابه هستند. به عنوان مثال، در مجموعه داده‌های اسباب‌بازی در شکل ۲ که در آن ردیف‌ها مکان‌ها، ستون‌ها نشان‌دهنده مُهر زمان، و مقادیر نشان‌دهنده دما هستند، مقادیر مشابه در مستطیل ضخیم چین‌خورده در شکل ۲ a را می‌توان با آن روش‌های هم‌خوشه‌بندی به‌عنوان یک خوشه مشترک شناسایی کرد. . با این حال، ممکن است در کشف هم‌خوشه‌هایی با روندهای منسجم شکست بخورند، که در آن زیر مجموعه‌های مهر زمانی فقط در زیر مجموعه‌های مکان‌ها رفتار متفاوت مشابهی دارند، به عنوان مثال، مقادیر خط چین ضخیم در شکل ۲ب در اینجا، روند منسجم به عنوان نشان دادن تمایلات مشابه در مقادیر ویژگی(ها) تعریف می شود [ ۲۰ ، ۲۱ ]. شناسایی هم‌خوشه‌ها با روندهای منسجم برای کمک به کشف الگوها در بسیاری از کاربردها مهم است. به عنوان مثال اقلیم شناسی را در نظر بگیرید، مطالعه روند دما توجه محققان را به خود جلب کرده است زیرا مشخص شد که تأثیراتی بر عملکرد محصول، پویایی جمعیت حشرات و حتی مرگ و میر بالای افراد مسن مبتلا به بیماری مزمن دارد [ ۲۲ ، ۲۳ ، ۲۴ ، ۲۵ ].]. علاوه بر این، تجزیه و تحلیل جرم می‌تواند از چنین روش هم‌خوشه‌بندی سود ببرد، به این صورت که روندهای مشابه شناسایی شده در مکان‌های مختلف به پلیس کمک می‌کند تا حرکت گانگسترها را بررسی کند و اقدامات مربوطه را به طور موثر انجام دهد [ ۲۶ ]. بنابراین، استفاده از یک روش هم‌خوشه‌بندی که قادر به شناسایی هم‌خوشه‌هایی با رفتارهای متفاوت مشابه در داده‌های مکانی-زمانی باشد، ضروری است.

برخلاف روش‌های هم‌خوشه‌بندی فوق‌الذکر که به دنبال شباهت زیاد مقادیر در هم‌خوشه هستند، روش‌های هم‌خوشه‌بندی برای روندهای منسجم، امتیاز بالایی از انسجام در هم‌خوشه را هدف قرار می‌دهند [ ۲۷ ]. همانطور که توسط آیزن و همکاران بیان شده است. [ ۲۰ ]، روند منسجم سری های اندازه گیری را می توان با روش های مختلفی محاسبه کرد، به عنوان مثال، فواصل اقلیدسی، ضریب همبستگی و غیره. چنگ و چرچ [ ۲۸ ] باقیمانده را به عنوان اندازه گیری فاصله برای کمی کردن روند منسجم برای هم خوشه ها معرفی کردند. باقیمانده به عنوان تفاوت بین هر عنصر در هم‌خوشه و میانگین ردیف و همچنین میانگین ستون [ ۲۹ ] نامیده می‌شود. مجموعه داده اسباب بازی در شکل ۲ را در نظر بگیریدb برای مثال، انتساب خوشه بندی {۱۱۲۲} برای ردیف ها و {۱۱۱۲۲۲} برای ستون ها، با در نظر گرفتن توزیع سطر و ستون مجموعه داده ترجیح داده می شود. با چنین تخصیصی، مقادیر مستطیل چین دار ضخیم در شکل ۲ b به عنوان یک هم خوشه تقسیم می شود و باقیمانده عناصر در هم خوشه برابر با صفر است.

مطالعات متعددی بر روی روش‌های هم‌خوشه‌بندی با روندهای منسجم برای کاوش الگوهای منسجم، به‌ویژه در زمینه تحلیل ریزآرایه، کار کرده‌اند. همانطور که قبلاً ذکر شد، چنگ و چرچ [ ۲۸ ] ابتدا الگوریتم هم‌خوشه‌بندی باقیمانده حداقل مجموع مربع (MSSRCC) را برای جستجوی الگوهای هم‌تنظیمی در داده‌های بیان پیشنهاد کردند. چو و دیلون [ ۳۰ ] MSSRCC را با استراتژی‌های مختلف، به‌عنوان مثال، جستجوی محلی افزایشی، برای جستجوی هم‌خوشه‌های منسجم در هر دو مجموعه داده‌های بیان ژن مصنوعی و چندگانه به کار بردند. یانگ و همکاران [ ۳۱] یک الگوریتم هم‌خوشه‌بندی به نام خوشه‌بندی همپوشانی انعطاف‌پذیر را معرفی کرد که همه هم‌خوشه‌های همپوشانی را که میانگین باقیمانده‌های آن‌ها کوچک‌تر از یک مقدار از پیش تعریف‌شده است برای کشف الگوهای منسجم در داده‌های بیان ژن به دست می‌دهد. کلوگر و همکاران [ ۳۲ ] یک الگوریتم هم‌خوشه‌بندی طیفی پیشنهاد کرد که یک بردار منفرد از داده‌های بیان ژن نرمال‌شده را محاسبه می‌کند، داده‌ها را بر روی بالاترین بردارها پروژه می‌دهد و سپس برش‌های نرمال‌شده را اعمال می‌کند. راتیپریا و همکاران [ ۳۳ ] یک الگوریتم هم‌خوشه‌بندی مبتنی بر بهینه‌سازی ازدحام ذرات باینری ایجاد کرد که تکنیک هوشمند ازدحام و هم‌خوشه‌سازی را برای کشف روابط منسجم بین کاربران وب و صفحات وب ترکیب می‌کند.

بنابراین، هدف این مطالعه استفاده از یک روش هم‌خوشه‌بندی برای داده‌های مکانی-زمانی است که امکان شناسایی هم‌خوشه‌های مکانی-زمانی با روندهای منسجم را فراهم می‌کند. در اینجا، ما روی سری‌های زمانی ارجاع‌شده جغرافیایی تمرکز می‌کنیم، یک نوع مهم از داده‌های مکانی-زمانی، که معمولاً در مکان‌های ثابت و مهرهای زمانی با فواصل یکنواخت ثبت می‌شوند. سری دمای ماهانه هلندی برای نشان دادن روش هم‌خوشه‌بندی استفاده می‌شود. تا آنجا که می دانیم، هیچ یک از مطالعات قبلی هم خوشه هایی را با روندهای منسجم در داده های مکانی-زمانی شناسایی نکردند. تازگی این تحقیق در سه جنبه زیر نهفته است: (۱) یک الگوریتم هم‌خوشه‌بندی که شناسایی هم‌خوشه‌ها را با روندهای منسجم امکان‌پذیر می‌سازد، برای تحلیل سری دمای هواشناسی هلندی معرفی می‌شود. (۲) ۱۱۲ خوشه مشترک با تغییرات دمایی مختلف توسط الگوریتم هم‌خوشه‌بندی شناسایی شد و هفت نوع روند دمایی منسجم خلاصه شد. (۳) مقایسه با هم‌خوشه‌های مقادیر مشابه، تفاوت‌های بین این دو نوع روش را نشان می‌دهد.

بقیه این مقاله به شرح زیر سازماندهی شده است. بخش ۲ مجموعه داده دمای هلند و الگوریتم هم‌خوشه‌بندی خاص مورد استفاده در این مطالعه را توصیف می‌کند. بعد، بخش ۳ نتایج تجزیه و تحلیل هم‌خوشه‌بندی سری دمای هلندی را ارائه می‌کند و تفاوت‌های بین هم‌خوشه‌ها با مقادیر مشابه و روندهای منسجم را مورد بحث قرار می‌دهد. در نهایت، بخش ۴ نتیجه گیری می کند.

۲٫ داده ها و روش ها

این بخش ابتدا مجموعه داده و منطقه مورد مطالعه مورد استفاده برای نشان دادن این مطالعه را ارائه می دهد. پس از آن، الگوریتم هم‌خوشه‌بندی خاص، به نام الگوریتم هم‌خوشه‌سازی برگمن، با حداقل باقیمانده مجموع مجذور به تفصیل شرح داده می‌شود.

۲٫۱٫ داده ها

دمای ماهانه از ژانویه ۱۹۹۲ تا دسامبر ۲۰۱۱ در ۲۸ ایستگاه هواشناسی در هلند به عنوان مجموعه داده مطالعه موردی برای نشان دادن شناسایی هم‌خوشه‌ها با روندهای منسجم استفاده شد. داده‌های اولیه دمای روزانه به‌طور رایگان در وب‌سایت مؤسسه هواشناسی سلطنتی هلند (KNMI، https://dataplatform.knmi.nl/ (دسترسی در ۱۴ فوریه ۲۰۲۲) در دسترس بود)، که سپس برای تولید میانگین دمای ماهانه میانگین‌گیری شد. نقشه چند ضلعی های تیسن ( شکل ۳ ) با استفاده از مختصات ایستگاه ها برای تعریف ناحیه ای که هر ایستگاه روی آن تأثیر داشت، ایجاد شد، به عنوان مثال، چند ضلعی برجسته که ناحیه تحت تأثیر ایستگاه Schiphol را نشان می دهد (۲۴۰).

هلند به عنوان منطقه مورد مطالعه برای موقعیت آن انتخاب شد. با دریای شمال به عنوان همسایه آن در شمال و غرب و همچنین بلژیک و آلمان به ترتیب در جنوب و شرق همسایه، آب و هوای هلند تحت تأثیر آب و هوای معتدل دریایی در غرب و آب و هوای قاره ای در غرب است. شرق در نتیجه دما به تدریج از جنوب غرب به شمال شرق این کشور تغییر می کند.

۲٫۲٫ الگوریتم هم‌خوشه‌بندی برگمن با حداقل مجذور باقیمانده (BCC_MSSR)

بر خلاف روش‌های هم‌خوشه‌بندی که هم‌خوشه‌هایی را با مقادیر مشابه شناسایی می‌کنند، روش‌های هم‌خوشه‌سازی برای کاوش رفتار متغیر منسجم محلی برای هم‌خوشه‌هایی با روندهای مشابه جستجو می‌کنند. با نگاشت مکان‌ها به خوشه‌های مکان و مُهرهای زمانی به خوشه‌های مُهر زمانی، آن‌ها منجر به هم‌خوشه‌هایی در هر کدام می‌شوند که گرایش‌های ویژگی(ها) مشابه بودند. از MSSRCC در این مطالعه استفاده می شود زیرا اعتبار آن به طور تجربی در چندین مجموعه داده بهبود یافته است و به عنوان الگوریتم هم خوشه بندی برگمن با حداقل مجموع مجذور باقیمانده (BCC_MSSR) به دنبال کار [ ۲۷ ] نامیده می شود.]. بر خلاف واگرایی اطلاعاتی مورد استفاده در الگوریتم هم‌خوشه‌بندی میانگین بلوکی برگمن با واگرایی I (BBAC_I) که هم‌خوشه‌هایی را با مقادیر مشابه شناسایی کرد، باقیمانده به عنوان اندازه‌گیری فاصله روندهای منسجم در هم‌خوشه‌ها برای BCC_MSSR استفاده شد. قبلا ذکر شده. سپس باقیمانده مجموع مربع به عنوان مجموع واریانس‌های مجذور هر عنصر در هم‌خوشه و میانگین ردیف و میانگین ستون مطابق تعریف شد، که برای ساخت تابع هدف قبل و بعد از نگاشت استفاده شد. بهینه‌سازی موضوع هم‌خوشه‌بندی را می‌توان به عنوان مشکل به حداقل رساندن مجذور کل باقیمانده در نظر گرفت.

الگوریتم BCC_MSSR شناسایی هم‌خوشه‌ها را با روندهای منسجم در هر ماتریس داده با ارزش واقعی امکان‌پذیر می‌سازد. سری دمای ماهانه هلندی مورد استفاده در مطالعه موردی را می‌توان به‌عنوان یک ماتریس همزمانی بین دو متغیر سازمان‌دهی کرد: ایستگاه‌ها (S) مقادیر را در مجموعه ایستگاه‌ها {۱، ۲، …، z}، و ماه‌ها (M) مقادیر را دریافت می‌کنند. در تمام ماه ها به عبارت دیگر، سری دما را می توان به عنوان ماتریس داده رسمی کرد . فرض کنید ایستگاه‌ها و ماه‌ها به ترتیب به k و l، ایستگاه-خوشه و ماه-خوشه در تحلیل هم‌لوسترینگ نگاشت شده‌اند. سپس، ماتریس داده‌ها پس از هم‌خوشه‌بندی است ، با گرفتن مقادیر در مجموعه های ایستگاه-خوشه {۱، ۲، …، k} و گرفتن مقادیر در مجموعه های ماه خوشه {۱، ۲، …، l}.

فرض کنید که I و J به ترتیب مجموعه شاخص‌های مکان‌ها را در یک خوشه مکان و مجموعه شاخص‌های مُهرهای زمانی را در یک خوشه زمانی نشان می‌دهند. باقیمانده یک عنصر خاص، ، در یک هم خوشه به صورت محاسبه می شود

(۱)

جایی که میانگین عناصر ایستگاه i را نشان می دهد که شاخص های ماه آنها در J قرار می گیرد. میانگین عناصر در ماه j را نشان می دهد که شاخص های ایستگاه آنها در I قرار می گیرد و میانگین تمام عناصر در آن خوشه مشترک را نشان می دهد. ماتریس باقی مانده H را می توان به صورت نمایش داد ، که در آن R و C ردیف ها (ایستگاه ها) و ستون ها (ماه) ماتریس های شاخص خوشه ای با اندازه z × k و n × l هستند، و ماتریس انتقال یافته از R است.

سپس، تابع هدف BCC_MSSR به عنوان باقیمانده مجموع دو عناصر قبل و بعد از هم‌خوشه‌بندی نشان داده می‌شود:

(۲)

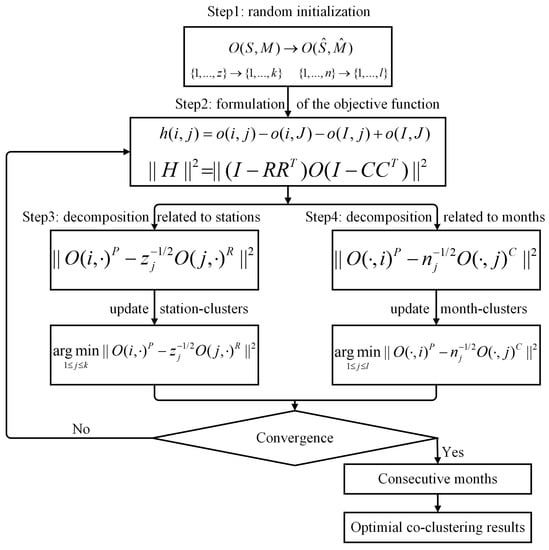
جایی که نشان دهنده هنجار یک ماتریس است، به عنوان مثال، . سپس، مشکل هم‌خوشه‌سازی به موضوع کمینه‌سازی تبدیل می‌شود. برای به حداقل رساندن تابع هدف برای به دست آوردن نتایج هم‌خوشه‌بندی بهینه، BCC_MSSR با یک فرآیند تکراری طراحی شد. روش بهینه‌سازی این الگوریتم هم‌خوشه‌بندی در مراحل زیر توضیح داده شده است ( شکل ۴ ):

مرحله ۱: مقداردهی اولیه تصادفی خوشه های ایستگاه و خوشه های ماه به طور تصادفی به ایستگاه ها و خوشه های ماه نگاشت شدند که R و C اولیه را ایجاد کردند .

مرحله ۲: محاسبه باقیمانده و تابع هدف. باقیمانده هر عنصر و همچنین باقیمانده مجموع دو عناصر قبل و بعد از نقشه برداری محاسبه شد که می تواند بیشتر به صورت نمایش داده شود.

(۳)

مرحله ۳: نقشه برداری را از ایستگاه ها به ایستگاه ها به روز کنید. معادله (۳) ابتدا به باقی مانده مجموع مربع مربوط به ردیف ها (ایستگاه ها) تجزیه شد [ ۳۰ ]:

(۴)

جایی که ، و ردیف i (ایستگاه) را مشخص کنید . سپس، عضویت جدید ایستگاه-خوشه ها را می توان با کمینه کردن معادله (۴) به روز کرد:

(۵)

مرحله ۴: نقشه برداری را از ماه به خوشه ماه به روز کنید. معادله (۳) را می توان به باقی مانده مجموع مربع مربوط به ستون ها (ماه) نیز تجزیه کرد:

(۶)

مرحله ۵: محاسبه مجدد باقیمانده و تابع هدف. باقیمانده و تابع هدف با استفاده از خوشه ایستگاه و ماه خوشه به روز شده دوباره محاسبه شد. هنگامی که تابع هدف با تغییر تابع زیر یک آستانه به همگرایی رسید، خوشه های ایستگاه و خوشه ماه بهینه به دست آمد. در غیر این صورت، مراحل ۳-۵ را تا زمان همگرایی تکرار کنید. از آنجایی که روند داده‌های سری زمانی ارجاع‌شده جغرافیایی به مهرهای زمانی متوالی نیاز دارد، با انتخاب آن‌هایی که ماه‌های متوالی دارند، چنین محدودیتی برای خوشه‌های ماه در نتایج هم‌خوشه‌بندی اضافه شد. در نهایت، نتایج هم‌خوشه‌بندی بهینه به دست آمد.

هم Banerjee، Dhillon، Ghosh، Merugu و Modha [ ۲۷ ]، و Cho and Dhillon [ ۳۰ ] ثابت کردند که تابع هدف در معادله (۳) می تواند به همگرایی دست یابد، زیرا به طور یکنواخت با تکرار به حداقل رسیده است. با این حال، از آنجایی که الگوریتم خوشه‌بندی به صورت محلی بهینه‌سازی شده بود، کل فرآیند بهینه‌سازی معمولاً با اجرای چندگانه تکرار می‌شد تا نتایج هم‌خوشه‌بندی بهینه به دست آید. در پایان شایان ذکر است که در این تحقیق از MATLAB نسخه R2019b برای پیاده سازی الگوریتم هم خوشه بندی استفاده شده است و کدها در صورت درخواست معقول در دسترس هستند.

۳٫ نتایج و بحث

داده های دمای ماهانه با اندازه ۲۸ (ایستگاه) × ۲۴۰ (ماه) توسط BCC_MSSR برای شناسایی هم خوشه های مکانی-زمانی با روند منسجم تجزیه و تحلیل شد. تعداد خوشه های ایستگاه و خوشه ماه با استفاده از روش silhouette و k-means بهینه شدند. روش silhouette استفاده شد زیرا می تواند نتایج خوشه بندی را تولید کند که همبستگی بالایی با قضاوت متخصصان دارد [ ۳۴ ، ۳۵ ]. دو تا پانزده با فاصله یک به عنوان اعداد کاندیدای ایستگاه-خوشه و ماه-خوشه استفاده شد. با عدد چهار برای هر دو ایستگاه-خوشه و ماه-خوشه، روش silhouette 0.6492 و ۰٫۷۲۵۲ را به عنوان بالاترین مقادیر به دست آورد. بنابراین، چهار به عنوان عدد بهینه برای هر دو خوشه ایستگاه و خوشه ماه انتخاب شد.

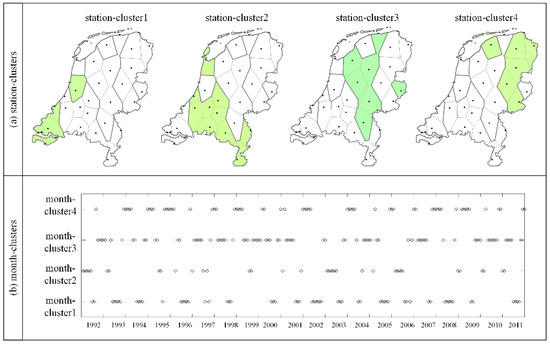
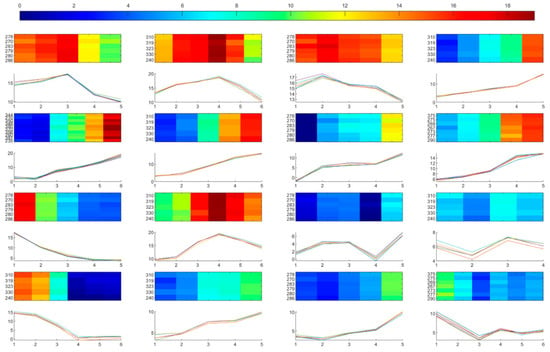
پس از تجزیه و تحلیل هم‌خوشه‌بندی، ۲۸ ایستگاه و ۲۴۰ ماه به ترتیب به چهار ایستگاه-خوشه و چهار ماه-خوشه ترسیم شدند که با استفاده از مضرب کوچک و نمودارهای الماسی در شکل ۵ و شکل ۶ نمایش داده شده‌اند . هم‌خوشه‌ها با هر ایستگاه-خوشه و هر مجموعه از ماه‌های متوالی در خوشه‌های ماه در این شرایط قطع شدند. با توجه به حداقل موضوع محلی/جهانی موجود در همه الگوریتم‌های خوشه‌بندی [ ۱۵ ]، ما روی برخی از خوشه‌های مشترک که اغلب در نتایج BCC_MSSR ظاهر می‌شوند تمرکز می‌کنیم. آن دسته از هم‌خوشه‌ها با استفاده از نقشه‌های حرارتی و نمودارهای خطی در شکل ۷ نمایش داده می‌شوند .

۳٫۱٫ هم‌خوشه‌های مکانی-زمانی با روندهای منسجم

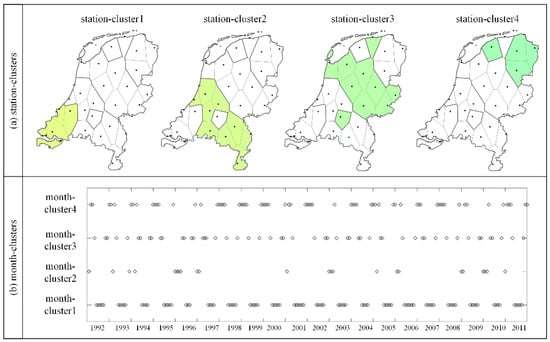
شکل ۵ a توزیع فضایی چهار ایستگاه-خوشه بر روی هلند را با رنگ نشان می دهد. کل کشور به چهار منطقه از جنوب غربی تا شمال شرقی تقسیم شد. برخلاف الگوهای افزایش دما که در نتایج تجزیه و تحلیل هم‌خوشه‌بندی قبلی سری دمای هلندی یافت می‌شود [ ۱۴ ، ۳۶]، هیچ الگوی افزایش یا کاهش دما در این چهار منطقه در این مطالعه وجود نداشت. به این دلیل است که این چهار ایستگاه-خوشه بر اساس تغییرات دما تقسیم شده اند و ممکن است دو ایستگاه با تغییرات دمایی مشابه دارای مقادیر دمایی متفاوتی باشند. ایستگاه‌های هر منطقه دارای تغییرات دمایی مشابهی هستند، به عنوان مثال، Schipol (240)، Hoek van Holland (330)، Wilhelminadorp (323)، Vlissigen (310)، و Westdorpe (319) در ایستگاه-خوشه ۱٫ اکثر ایستگاه ها در هر ایستگاه-خوشه مجاور بودند، به جز Schipol (240) در ایستگاه-خوشه ۱، De Kooy (235) در ایستگاه-خوشه۲، Twenthe (290) در ایستگاه-خوشه ۳، و Leeuwarden (270) در ایستگاه-خوشه ۴٫

توزیع زمانی عناصر در هر یک از خوشه های ماه در طول ۲۴۰ ماه در شکل ۵ ب نشان داده شده است. به دلیل انتساب BCC_MSSR، ماه ها همیشه در خوشه های ماه متوالی نبودند. با توجه به نیاز به مهرهای زمانی متوالی، ما آن ماه هایی را که حداقل برای چهار مهر زمانی متوالی در هر خوشه ماه بودند، به عنوان ماه های بالقوه برای ساخت خوشه های مشترک با تغییرات دمایی مشابه انتخاب کردیم. برای توضیح بیشتر وضعیت، توزیع زمانی ماه‌ها در ماه خوشه ۱ و ماه خوشه ۳ در ۲۴۰ ماه در ۲۰ سال در شکل ۶ نشان داده شده است.که به موجب آن محور x 12 ماه و محور y 20 سال است. می‌توانیم ببینیم که ماه‌ها در month-cluster1 عمدتاً در تابستان توزیع شده‌اند. اگرچه طول ماه های متوالی در ماه-خوشه ۱ متفاوت بود، اما آنها همچنان تغییرات دمایی مشابهی داشتند، به عنوان مثال، می تا سپتامبر ۲۰۰۸ و می تا اکتبر ۲۰۰۲٫ همچنین قابل ذکر است که ماه های متوالی در دو سال انتقال نیز در نظر گرفته شده است. به عنوان ماه های بالقوه، به عنوان مثال، سپتامبر ۲۰۰۴ تا ژانویه ۲۰۰۵٫ با توجه به معیارهای ماه های بالقوه برای ساخت هم خوشه ها، ۲۸ مجموعه از ماه های متوالی انتخاب شدند. در نتیجه، ۱۱۲ خوشه مشترک (۲۸ × ۴ ایستگاه-خوشه) با تغییرات دمایی مشابه تولید شد. به دلیل فضای محدود، ۱۶ هم‌خوشه نماینده نمایش داده می‌شوند ( شکل ۷) و هم‌خوشه‌های مشابه در متن توضیح داده شده‌اند.

شکل ۷ آن ۱۶ خوشه نماینده را با روندهای دمایی متفاوت در بین آنها نشان می دهد. روندها در هر خوشه مشابه بود. یک نقشه حرارتی و یک نمودار خطی برای نمایش هر خوشه مشترک استفاده شد: نقشه حرارتی در بالا نمای مستقیم هم‌خوشه را فراهم می‌کند، با محور x تعداد ماه‌های متوالی و محور y ایستگاه‌های درگیر را نشان می‌دهد. در حالی که نمودار خطی زیر روندهای دمایی هم‌خوشه را نشان می‌دهد، با محور y که مقادیر دما را نشان می‌دهد.

به طور کلی، عمدتاً هفت نوع روند دمایی منسجم در هم‌خوشه‌های نماینده وجود دارد که بر اساس درجه پیچیدگی به شرح زیر رتبه‌بندی می‌شوند: (۱) افزایش. (۲) کاهش؛ (۳) ابتدا افزایش و سپس کاهش. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. (۷) ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش. همانطور که در شکل ۷ نشان داده شده استهم‌خوشه‌های چهارم تا هشتم همگی روند افزایشی دما را نشان می‌دهند، حتی با دامنه‌های مختلف دما و تفاوت در افزایش سرعت. ایستگاه‌های درگیر آن ایستگاه‌هایی در بخش جنوب غربی هلند بودند و ماه‌های درگیر ژانویه تا مه ۱۹۹۲ بودند. چنین روند افزایشی دما در زمستان و اوایل بهار ممکن است باعث شروع زودتر و گسترش فصل رشد در استان‌های نزدیک به خط ساحلی شود. ۳۷]. هم‌خوشه‌هایی با روند دمایی مشابه، تقاطع‌های ایستگاه-خوشه ۱، فوریه تا ژوئن ۲۰۰۶، و فوریه تا می ۲۰۱۱ بودند. در هشتمین هم‌خوشه، می‌توانیم ببینیم که سرعت ابتدا ثابت است، سپس شتاب گرفت و در نهایت کاهش یافت. . ایستگاه های درگیر ایستگاه های مرکز شمال شرق کشور و ماه های درگیر فوریه تا ژوئن ۱۹۹۸ بودند. خوشه های مشترک با روند منسجم مشابه، تقاطع ایستگاه-خوشه ۳ در مرکز- شمال شرق، فوریه تا جولای ۲۰۰۷ بودند. و فوریه تا مه ۲۰۱۱٫ هم‌خوشه‌ای که روند کاهشی دما را نشان می‌دهد، نهمین خوشه با منحنی‌های نزولی هموار بود. ایستگاه های درگیر همان ایستگاه های شمال شرق کشور و ماه های درگیر از سپتامبر ۱۹۹۹ تا ژانویه ۲۰۰۰ بودند.۳۷ ، ۳۸ ].

چندین هم‌خوشه ابتدا روند افزایشی و سپس کاهشی دما را در شکل ۷ نشان می‌دهند.یعنی اول تا سوم و دهم با محدوده دماهای مختلف. هم خوشه های اول تا سوم با دمای نسبتاً بالا شروع می شوند، سپس افزایش می یابند و در نهایت کاهش می یابند. حتی با وجود این شباهت‌ها، باز هم در مُهرهای چرخشی برای کاهش و همچنین سرعت افزایش و کاهش متفاوت هستند. ایستگاه‌های درگیر هم‌خوشه اول و سوم، ایستگاه‌های شمال شرق کشور و ماه‌های درگیر به ترتیب خرداد تا مهر ۹۶ و اردیبهشت تا مهر ۱۳۸۴ بودند. ایستگاه‌های درگیر دومین هم‌خوشه ایستگاه‌هایی در جنوب غربی بودند و ماه‌های درگیر از می تا اکتبر ۲۰۰۲ بودند. هم‌خوشه‌هایی که روند دمایی مشابهی را نشان دادند، ایستگاه‌هایی در شمال شرقی، می تا اکتبر ۱۹۹۳، ژوئن تا اکتبر ۱۹۹۴، و می بودند. تا اکتبر ۲۰۰۸ دهمین هم خوشه با دمای پایین شروع شد و سپس افزایش یافت و در نهایت افت کرد. ایستگاه‌های درگیر این هم‌خوشه ایستگاه‌های جنوب غربی و ماه‌های درگیر از فروردین تا شهریور ۱۳۸۹ بودند. هم‌خوشه‌های سیزدهم و پانزدهم روند معکوس ابتدا کاهش و سپس افزایش را نشان می‌دهند. اگرچه آنها در یک نوع اصلی از روندهای منسجم طبقه بندی شدند، این دو خوشه مشترک دارای دامنه های دما و مدهای تغییر کاملاً متفاوتی هستند. با شروع دمای نسبتاً بالا، سیزدهمین هم خوشه به شدت سقوط کرد و سپس در پایان کمی افزایش یافت. ایستگاه‌های درگیر این هم‌خوشه ایستگاه‌های جنوب غربی و ماه‌های درگیر از شهریور ۹۵ تا بهمن ۹۶ بودند. برعکس، هم‌خوشه پانزدهم با دمای پایین شروع و سپس کاهش یافت.

سایر هم‌خوشه‌ها تغییرات دمایی پیچیده‌تری را نشان دادند. به عنوان مثال، خوشه های هفتم، یازدهم و چهاردهم ابتدا روند افزایشی، سپس کاهشی و در نهایت افزایشی را نشان می دهند. اگرچه با کمی تفاوت در مقادیر شروع و محدوده دما، هم خوشه های هفتم و چهاردهم حالت مشابهی از تغییرات داشتند. ایستگاه های درگیر هم خوشه هفتم و چهاردهم به ترتیب ایستگاه های شمال شرق و جنوب غرب کشور بودند. ماه های درگیر ژانویه تا مه ۱۹۹۷ برای اولی و دسامبر ۲۰۰۱ تا آوریل ۲۰۰۲ برای دومی بود. در مقایسه با این دو خوشه، هم‌خوشه یازدهم دامنه‌های دما کمتری داشت اما تغییرات شدیدتری داشت. ایستگاه های درگیر این هم خوشه ایستگاه هایی در شمال شرقی هلند بودند. و ماههای درگیر نوامبر ۱۹۹۳ تا مارس ۱۹۹۴ بودند. دوازدهمین هم خوشه ابتدا روندهای دما کاهشی، سپس افزایشی و در نهایت کاهشی را نشان می دهد. اگرچه با دامنه کوچک دماهای پایین، این خوشه از تغییرات شدید محلی عبور می کند. ایستگاه‌های درگیر این هم‌خوشه ایستگاه‌های جنوب غرب کشور و ماه‌های درگیر آذر ۹۴ تا اسفند ۹۵ بودند. هم‌خوشه‌هایی که روند دمایی مشابهی را نشان می‌دهند ایستگاه‌هایی در جنوب غرب و آبان ۱۳۷۷ تا اسفند ۱۳۷۸ بودند. در پیچیده‌ترین روندهای دما، شانزدهمین هم‌خوشه ابتدا کاهش، سپس افزایش، کاهش و در نهایت افزایش تغییرات را تجربه کرد. ایستگاه های درگیر این هم خوشه ایستگاه هایی در مرکز-جنوب غربی هلند بودند.۳۹ ].

۳٫۲٫ الگوهای منطقه ای منسجم فضایی-زمانی در سری دمای ماهانه هلندی

با ترکیب شکل ۵ ، شکل ۶ و شکل ۷ ، می بینیم که حتی اگر پوشش فضایی هلند نسبتاً کوچک است، این کشور الگوهای دمایی منسجم منطقه ای پیچیده ای را در مناطق مختلف و دوره های خاص نشان می دهد. فاصله تا ساحل رابطه منفی با تغییرپذیری دما را نشان می دهد [ ۴۰]. نزدیک به ساحل و بیشتر تحت تأثیر آب و هوای دریایی مستقیماً، بخش جنوب غربی هلند عمدتاً الگوهای دما را از می تا اکتبر ۲۰۰۲ و ۲۰۱۰ کاهش می‌دهد. مرکز-جنوب غربی کشور الگوهای اول را نشان می‌دهد. کاهش، سپس افزایش، کاهش و در نهایت افزایش الگوهای دما از اکتبر ۲۰۰۷ تا مارس ۲۰۰۸٫ بخش مرکزی-شمال شرقی هلند عمدتاً الگوهای افزایش دما را از فوریه تا ژوئن ۱۹۹۸ و ۲۰۰۷ نشان می‌دهد، که ما فرض می‌کنیم دلیل اولیه آن است. شروع فصل گرده در اطراف این منطقه [ ۴۱]. بخش شمال شرقی کشور عمدتاً الگوهای کاهش دما را از سپتامبر ۱۹۹۹ و ۲۰۰۳ تا ژانویه سال آینده نشان می دهد، که فکر می کنیم بر عملکرد محصول و همچنین اقتصاد استان های شمالی که کشاورزی منبع اصلی درآمد است، تأثیر گذاشته است [ ۴۲ ].

۳٫۳٫ مقایسه خوشه‌های مشترک با روندهای منسجم و آنهایی که دارای ارزش‌های مشابه هستند

همانطور که ذکر شد، مطالعاتی در مورد شناسایی هم‌خوشه‌هایی با مقادیر مشابه در داده‌های مکانی-زمانی انجام شده است [ ۱۴ ، ۱۷ ، ۱۹ ]. در این بخش، نتایج هم‌خوشه‌ها را با روند مشابه و هم‌خوشه‌هایی با مقادیر مشابه مقایسه می‌کنیم. برای این منظور، الگوریتم هم‌خوشه‌بندی میانگین بلوکی برگمن با واگرایی I (BBAC_I) [ ۱۴ ] برای همان مجموعه داده دمای ماهانه هلندی مورد استفاده در مطالعه موردی اعمال شد. برای مقایسه، تعداد خوشه های ایستگاه و خوشه ماه هر دو به عنوان چهار تعیین شد. مقایسه‌ها از نظر ایستگاه-خوشه، ماه-خوشه، هم-خوشه، و الگوهای کاوش شده انجام شد.

ایستگاه-خوشه و ماه-خوشه در نتایج BBAC_I در شکل ۸ نمایش داده شده است. در بعد ایستگاه-خوشه ها، نمای کلی چهار ایستگاه-خوشه ( شکل ۸الف) با نتایج BCC_MSSR مشابه نبودند. اگرچه چهار منطقه از شمال شرقی به جنوب غربی تقسیم شدند، اما الگوهای افزایش دما را نشان دادند. علاوه بر این، ترکیب و توزیع فضایی هر ایستگاه-خوشه بین دو نتیجه متفاوت بود. برای ایستگاه-خوشه ها در BBAC_I، آنها در فضا فشرده تر بودند و بیشتر عناصر در هر ایستگاه-خوشه مجاور بودند. بر خلاف آنها، توزیع فضایی ایستگاه ها در هر ایستگاه-خوشه در BCC_MSSR از جنوب به شمال، به ویژه در ایستگاه-خوشه های ۲ و ۳ بیشتر بود. در واقع، ترکیب و توزیع فضایی ایستگاه-خوشه ها در BBAC_I نتایج مشابه نتایج BBAC_I دمای سالانه هلند در وو، زوریتا-میلا و کراک [ ۱۴ ] بود.] نسبت به نتایج BCC_MSSR در این مطالعه. ما فرض می کنیم که به این دلیل است که مقادیر دما بیشتر تحت تأثیر اقلیم های مختلف قرار گرفته است، به عنوان مثال، آب و هوای معتدل دریایی و قاره ای در هلند، در حالی که روندهای دما در طول طول جغرافیایی متغیرتر است [ ۴۳ ]. ترکیب و توزیع زمانی خوشه های ماه در نتایج BBAC_I ( شکل ۸ ب) نیز با خوشه های ماه در نتایج BCC_MSSR متفاوت بود.

حتی اگر نام هم‌خوشه‌ها با روندهای منسجم و هم‌خوشه‌ها با مقادیر مشابه به خودی خود تفاوت‌ها را نشان می‌دهند، نقشه‌های حرارتی برای ارائه دیدگاه ساده‌تری از تفاوت‌های بین این دو مورد استفاده قرار گرفتند. برای این هدف، دو عنصر در co-cluster2 ({Rotterdam (344)، سپتامبر ۲۰۰۰} و {Herwijnen (356)، ژانویه ۲۰۰۱}) در نتایج BCC_MSSR و هم‌خوشه‌های مربوط به هر عنصر در نتایج BBAC_I هستند. در شکل ۹ به عنوان نمونه نمایش داده شده است. همانطور که در سمت چپ شکل ۹ نشان داده شده استدو عنصر دارای مقادیر دمایی کاملاً متفاوتی هستند و در نتایج BCC_MSSR به دلیل تغییرات مشابهی که توسط هم‌خوشه نشان داده می‌شود، به یک هم‌خوشه تقسیم شدند، یعنی به سرعت از بین می‌روند و سپس کمی افزایش می‌یابند. با این حال، در نتایج BBAC_I که در آن هم‌خوشه‌ها با مقادیر مشابه تقسیم شدند، دو عنصر به هم‌خوشه‌های مختلف تقسیم شدند. عنصر {روتردام (۳۴۴)، سپتامبر ۲۰۰۰} متعلق به یک هم خوشه با تمام دماهای بالا به عنوان عناصر بود، در حالی که عنصر {Herwijnen (356)، ژانویه ۲۰۰۱} متعلق به هم خوشه دیگری با دمای پایین بود.

از نظر الگوهای کاوش شده، نتایج BBAC_I الگوهای مکانی- زمانی را در کل منطقه مورد مطالعه و دوره مورد مطالعه کشف کردند، یعنی روند کاهشی دما از جنوب غرب به شمال شرق کشور و از ماه-خوشه ۱ به ماه-خوشه۴ ( شکل ۸ ). در مقایسه، نتایج BCC_MSSR الگوهای مکانی-زمانی منسجم منطقه‌ای را در بخشی از کل منطقه مورد مطالعه و دوره‌های زمانی خاص مورد بررسی قرار داد، به عنوان مثال، ابتدا الگوهای دما در بخش جنوب غربی کشور از ماه می تا اکتبر ۲۰۰۲ افزایش و سپس کاهش یافت ( شکل ۵ ). شکل ۶ و شکل ۷ ).

همانطور که در بالا توضیح داده شد، نتایج BCC_MSSR و BBAC_I از چند جنبه متفاوت هستند. با این حال، هیچ روش برتر برای همه کارها وجود ندارد. انتخاب روش‌های هم‌خوشه‌بندی مناسب باید به هدف تحقیق از کار خاص در دست بستگی داشته باشد [ ۸ ، ۴۴ ]. اگر هدف شناسایی مقادیر مشابه صفات در مجموعه داده باشد، به عنوان مثال، دمای بسیار بالا در تابستان، BBAC_I پیشنهاد می شود. اگر هدف تجزیه و تحلیل روندهای مشابه ویژگی در مناطق مختلف بود، به عنوان مثال، تغییرات دما در مکان‌های مختلف و تأثیرات بعدی آنها، آنگاه BCC_MSSR به عنوان روش مناسب در نظر گرفته می‌شود.

۴٫ نتیجه گیری

در این مطالعه ما الگوریتم هم‌خوشه‌بندی برگمن را با حداقل مجموع مجذور باقیمانده (BCC_MSSR) برای تحلیل سری‌های زمانی ارجاع‌شده جغرافیایی ارائه کردیم. برخلاف مطالعات قبلی هم‌خوشه‌بندی روی داده‌های مکانی-زمانی که هم‌خوشه‌هایی را با مقادیر مشابه شناسایی می‌کردند، BCC_MSSR شناسایی هم‌خوشه‌ها با روندهای منسجم را امکان‌پذیر می‌کند، که به عنوان نشان دادن تمایلات مشابه در ویژگی(ها) تعریف می‌شود. این الگوریتم با استفاده از باقیمانده به عنوان اندازه‌گیری فاصله برای کمی کردن روندهای منسجم، موضوع هم‌خوشه‌بندی را به‌عنوان به حداقل رساندن مجموع مجذور باقی مانده در نظر می‌گیرد. برای نشان دادن این مطالعه، دمای ماهانه هلندی بیش از ۲۰ سال در ۲۸ ایستگاه به عنوان مطالعه موردی مورد استفاده قرار گرفت. ایستگاه-خوشه ها، ماه-خوشه ها و هم-خوشه ها در نتایج با استفاده از مضرب های کوچک، نقشه های حرارتی و نمودارهای خطی نمایش داده شدند. سپس،

نتایج نشان می دهد که هلند به چهار منطقه (ایستگاه-خوشه) از جنوب غربی تا شمال شرقی تقسیم شده است و ایستگاه های داخل هر منطقه دارای تغییرات دمایی مشابهی هستند. در مجموع ۱۱۲ خوشه مشترک با تغییرات دمایی مختلف در میان آنها در مجموعه داده‌های دمای ماهانه هلندی شناسایی شد. ۱۶ هم خوشه نماینده نشان داده شد، و هفت نوع از روند دمای منسجم خلاصه شد: (۱) افزایش. (۲) کاهش؛ (۳) ابتدا افزایش و سپس کاهش. (۴) ابتدا کاهش و سپس افزایش. (۵) ابتدا افزایش، سپس کاهش، و در نهایت افزایش. (۶) ابتدا کاهش، سپس افزایش، و در نهایت کاهش. (۷) ابتدا کاهش، سپس افزایش، کاهش، در نهایت افزایش. مقایسه با هم‌خوشه‌های مقادیر مشابه نشان می‌دهد که دو نتیجه هم‌خوشه‌بندی متفاوت بودند: توزیع‌های فضایی ایستگاه‌-خوشه‌ها در BCC_MSSR در فضا کشیده‌تر بودند، و BCC_MSSR الگوهای مکانی-زمانی منسجم را در مناطق محلی و دوره‌های زمانی خاص کشف می‌کند. با این حال، انتخاب روش‌های هم‌خوشه‌بندی مناسب باید به هدف کار خاص در دست بستگی داشته باشد.

از آنجایی که برای اولین بار بود که BCC_MSSR برای سری‌های زمانی ارجاع‌شده جغرافیایی اعمال شد، در آینده مسیرهای زیر برای کار روی آن‌ها وجود دارد: (۱) در این مطالعه ما فقط از این الگوریتم هم‌خوشه‌بندی برای یک مجموعه داده کوچک استفاده کردیم. در مرحله بعد، ما قصد داریم BCC_MSSR را به یک مجموعه داده فضایی-زمانی بزرگتر اعمال کنیم تا مقیاس پذیری آن را آزمایش کنیم. (۲) علاوه بر سری های زمانی مرجع جغرافیایی، ما قصد داریم این الگوریتم را برای انواع دیگر داده های مکانی-زمانی، به عنوان مثال، مسیرها اعمال کنیم. (۳) ما قصد داریم نتایج این تحقیق را در کاربردهای وسیع تری قرار دهیم، به عنوان مثال، برای مطالعه تأثیرات روندهای دمایی مختلف به دست آمده بر عملکرد محصول در هلند.

منابع

ریبیرو دی آلمیدا، دی. د سوزا باپتیستا، سی. Gomes de Andrade، F. Soares, A. نظرسنجی در مورد کلان داده برای تجزیه و تحلیل مسیر. ISPRS Int. J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۸۸٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
لی، ز. یانگ، سی. لیو، ک. هو، اف. جین، بی. مقیاس‌گذاری خودکار Hadoop در ابر برای فرآیند کارآمد داده‌های مکانی بزرگ. ISPRS Int. J. Geo-Inf. ۲۰۱۶ ، ۵ ، ۱۷۳٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
لی، ز. تانگ، دبلیو. هوانگ، Q. شوک، ای. Guan، Q. مقدمه ای بر محاسبات کلان داده برای کاربردهای جغرافیایی. ISPRS Int. J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۴۸۷٫ [ Google Scholar ] [ CrossRef ]
شکر، س. جیانگ، ز. علی، RY; افتلی اوغلو، ای. تانگ، ایکس. گونتوری، VMV؛ ژو، X. داده کاوی فضایی-زمانی: یک دیدگاه محاسباتی. ISPRS Int. J. Geo-Inf. ۲۰۱۵ ، ۴ ، ۲۳۰۶-۲۳۳۸٫ [ Google Scholar ] [ CrossRef ]
هان، جی. کمبر، م. Pei, J. Data Mining Concepts and Techniques , ۳rd ed.; مورگان کافمن MIT Press: کمبریج، MA، ایالات متحده آمریکا، ۲۰۱۲٫ [ Google Scholar ]
تاتیانا، وی.ال. فلیکس، بی. فیلیپ، آر. ناتالیا، ا. گنادی، ا. آندریاس، K. Mobility Graphs: تجزیه و تحلیل بصری دینامیک تحرک توده از طریق نمودارهای فضایی-زمانی و خوشه بندی. IEEE Trans. Vis. نمودار کامپیوتری ۲۰۱۶ ، ۲۲ ، ۱۱-۲۰٫ [ Google Scholar ]
بره، DS; داونز، جی. Reader، S. خوشه بندی سلسله مراتبی فضا-زمان برای شناسایی خوشه ها در داده های نقطه ای مکانی-زمانی. ISPRS Int. J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۸۵٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
وو، ایکس. چنگ، سی. زوریتا میلا، ر. Song, C. مروری بر روش‌های خوشه‌بندی برای سری‌های زمانی جغرافیایی ارجاع‌شده: از خوشه‌بندی یک‌طرفه تا خوشه‌بندی مشترک و سه‌گانه. بین المللی جی. جئوگر. Inf. علمی ۲۰۲۰ ، ۳۴ ، ۱۸۲۲-۱۸۴۸٫ [ Google Scholar ] [ CrossRef ]
آندرینکو، جی. برم، اس. شرک، تی. فون لندزبرگر، تی. باک، پ. کیم، دی. Andrienko، N. فضا-در-زمان و نقشه های خودسازماندهی زمان-در-فضا برای کاوش الگوهای فضایی-زمانی. محاسبه کنید. نمودار انجمن ۲۰۱۰ ، ۲۹ ، ۹۱۳-۹۲۲٫ [ Google Scholar ] [ CrossRef ]
هاگناور، جی. Helbich، M. نقشه های خودسازماندهی سلسله مراتبی برای خوشه بندی داده های مکانی و زمانی. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۳ ، ۲۷ ، ۲۰۲۶–۲۰۴۲٫ [ Google Scholar ] [ CrossRef ]
لیو، ال. هو، تی. بائو، اس. وو، اچ. پنگ، ز. وانگ، آر. اثر متقابل مکانی-زمانی انتقال COVID-19 در ایالات متحده. ISPRS Int. J. Geo-Infation ۲۰۲۱ ، ۱۰ ، ۳۸۷٫ [ Google Scholar ] [ CrossRef ]
آحاس، ر. آسا، ا. سیلم، اس. Roosaare، J. شاخص های فصلی و فصل های مناظر استونی. Landsc. Res. ۲۰۰۵ ، ۳۰ ، ۱۷۳-۱۹۱٫ [ Google Scholar ] [ CrossRef ]
وو، ایکس. زوریتا میلا، ر. کراک، ام.-جی. کشف بصری همگام سازی در داده های آب و هوا در وضوح های زمانی متعدد کارتوگرافی. J. ۲۰۱۳ ، ۵۰ ، ۲۴۷-۲۵۶٫ [ Google Scholar ] [ CrossRef ]
وو، ایکس. زوریتا میلا، ر. کراک، ام.-جی. هم‌خوشه‌بندی سری‌های زمانی جغرافیایی ارجاع‌شده: کاوش الگوهای مکانی-زمانی در داده‌های دمای هلند بین المللی جی. جئوگر. Inf. علمی ۲۰۱۵ ، ۲۹ ، ۶۲۴-۶۴۲٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
وو، ایکس. زوریتا میلا، ر. کراک، ام.-جی. تحلیلی جدید از الگوهای فنولوژیکی بهار در اروپا بر اساس هم‌خوشه‌بندی جی. ژئوفیس. Res. Biogeosci. ۲۰۱۶ ، ۱۲۱ ، ۱۴۳۴-۱۴۴۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
وو، ایکس. چنگ، سی. کیائو، سی. آهنگ، C. تمایز فضایی-زمانی فنولوژی بهار در چین بر اساس دما و دوره نوری از سال ۱۹۷۹ تا ۲۰۱۸٫ Sci. علوم زمین چین ۲۰۲۰ ، ۶۳ ، ۱۴۸۵-۱۴۹۸٫ [ Google Scholar ] [ CrossRef ]
الله، س. داود، ح. داس، SC; خان، HN; خلیل، ع. تشخیص خوشه‌های بیماری فضا-زمان با اشکال و اندازه‌های دلخواه با استفاده از رویکرد هم‌خوشه‌بندی. ژئوسپات. شفا دادن. ۲۰۱۷ ، ۱۲٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
آندرئو، وی. Izquierdo-Verdiguier، E. زوریتا میلا، ر. رزا، آر. ریزولی، آ. پاپا، الف. شناسایی شرایط فضایی-زمانی مطلوب برای شیوع ویروس نیل غربی با هم‌خوشه‌بندی سری‌های زمانی شاخص‌های Modis LST. در مجموعه مقالات IGARSS 2018-2018 IEEE بین المللی زمین شناسی و سمپوزیوم سنجش از دور، والنسیا، اسپانیا، ۲۲ تا ۲۷ ژوئیه ۲۰۱۸؛ صص ۴۶۷۰–۴۶۷۳٫ [ Google Scholar ]
لیو، کیو. ژنگ، ایکس. استنلی، HE; شیائو، اف. لیو، دبلیو. چارچوب هم‌خوشه‌بندی فضایی-زمانی برای کشف الگوهای تحرک: مطالعه داده‌های تاکسی منهتن. دسترسی IEEE ۲۰۲۱ ، ۹ ، ۳۴۳۳۸–۳۴۳۵۱٫ [ Google Scholar ] [ CrossRef ]
آیزن، مگابایت؛ اسپلمن، پی تی. براون، PO; Botstein، D. تجزیه و تحلیل خوشه ای و نمایش الگوهای بیان ژنومی. Proc. Natl. آکادمی علمی ایالات متحده آمریکا ۱۹۹۸ ، ۹۵ ، ۱۴۸۶۳-۱۴۸۶۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کریگل، اچ.-پی. کروگر، پی. Zimek، A. خوشه‌بندی داده‌های با ابعاد بالا: نظرسنجی در مورد خوشه‌بندی زیرفضا، خوشه‌بندی مبتنی بر الگو، و خوشه‌بندی همبستگی. ACM Trans. بدانید. کشف کنید. داده ۲۰۰۹ ، ۳ ، ۱٫ [ Google Scholar ] [ CrossRef ]
لیانگ، ال. لی، ال. لیو، Q. تغییرپذیری بارش در شمال شرقی چین از سال ۱۹۶۱ تا ۲۰۰۸٫ J. Hydrol. ۲۰۱۱ ، ۴۰۴ ، ۶۷-۷۶٫ [ Google Scholar ] [ CrossRef ]
الکساندر، LV; یوتیلا، پ. Nicholls، N. تأثیر تغییرپذیری دمای سطح دریا بر دمای جهانی و شدت بارش. جی. ژئوفیس. Res. اتمس. ۲۰۰۹ ، ۱۱۴ ، ۱-۱۳٫ [ Google Scholar ]
Estay، SA; کلاویخو باکت، اس. لیما، م. Bozinovic، F. فراتر از میانگین: آزمون تجربی تغییرپذیری دما بر روی پویایی جمعیت Tribolium confusum. مردمی Ecol. ۲۰۱۰ ، ۵۳ ، ۵۳-۵۸٫ [ Google Scholar ] [ CrossRef ]
زانوبتی، ا. اونیل، ام اس؛ Gronlund، CJ; شوارتز، JD تغییر دمای تابستان و بقای طولانی مدت در میان افراد مسن مبتلا به بیماری مزمن. Proc. Natl. آکادمی علمی ایالات متحده آمریکا ۲۰۱۲ ، ۱۰۹ ، ۶۶۰۸-۶۶۱۳٫ [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
اندرسن، MA; مالسون، N. فصلی بودن جرم و تغییرات آن در فضا. Appl. Geogr. ۲۰۱۳ ، ۴۳ ، ۲۵-۳۵٫ [ Google Scholar ] [ CrossRef ]
بانرجی، ا. دیلون، آی. گوش، ج. مروگو، اس. Modha، DS یک رویکرد ماکزیمم آنتروپی تعمیم یافته برای هم‌خوشه‌بندی برگمن و تقریب ماتریس. جی. ماخ. فرا گرفتن. Res. ۲۰۰۷ ، ۸ ، ۱۹۱۹-۱۹۸۶٫ [ Google Scholar ]
چنگ، ی. کلیسا، GM Biclustering داده های بیان. در Proceedings of the Proceedings ISMB 2000, San Diego, CA, USA, 19-23 August 2000; صص ۹۳-۱۰۳٫ [ Google Scholar ]
چو، اچ. Dhillon، IS; گوان، ی. Sra, S. حداقل مجموع-مربع باقیمانده هم‌خوشه‌بندی داده‌های بیان ژن. در مجموعه مقالات کنفرانس بین المللی SIAM در سال ۲۰۰۴ در مورد داده کاوی. انجمن ریاضیات صنعتی و کاربردی (SIAM)، فیلادلفیا، PA، ایالات متحده آمریکا، ۲۲-۲۴ آوریل ۲۰۰۴٫ [ Google Scholar ]
چو، اچ. Dhillon، I. Cclustering ریزآرایه های سرطان انسانی با استفاده از جمع آوری حداقل مجذور باقی مانده. IEEE/ACM Trans. محاسبه کنید. Biol. بیوانفورم. ۲۰۰۸ ، ۵ ، ۳۸۵-۴۰۰٫ [ Google Scholar ] [ CrossRef ]
یانگ، جی. وانگ، اچ. وانگ، دبلیو. Yu, P. دو خوشه‌بندی پیشرفته در داده‌های بیان. در مجموعه مقالات سومین سمپوزیوم IEEE در بیوانفورماتیک و مهندسی زیستی، Bethesda، MD، ایالات متحده، ۱۲ مارس ۲۰۰۳٫ صص ۳۲۱-۳۲۷٫ [ Google Scholar ]
کلوگر، ی. بصری، ر. چانگ، جی تی. Gerstein، M. دو خوشه‌بندی طیفی داده‌های ریزآرایه: ژن‌ها و شرایط هم‌آرامش. ژنوم Res. ۲۰۰۳ ، ۱۳ ، ۷۰۳-۷۱۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
راتیپریا، ر. تانگاول، ک. باگیمانی، جی. بهینه‌سازی ازدحام ذرات باینری مبتنی بر دو خوشه‌بندی داده‌های استفاده از وب. بین المللی جی. کامپیوتر. Appl. ۲۰۱۱ ، ۲۵ ، ۴۳-۴۹٫ [ Google Scholar ] [ CrossRef ]
Rousseeuw, PJ Silhouettes: کمکی گرافیکی برای تفسیر و اعتبارسنجی تحلیل خوشه‌ای. جی. کامپیوتر. Appl. ریاضی. ۱۹۸۷ ، ۲۰ ، ۵۳-۶۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لوئیس، جی.ام. آکرمن، ام. Sa، VRD ارزیابی خوشه انسانی و معیارهای کیفیت رسمی: یک مطالعه تطبیقی. در مجموعه مقالات سی و چهارمین کنفرانس انجمن علوم شناختی (CogSci)، ساپورو، ژاپن، ۱-۴ اوت ۲۰۱۲٫ جلد ۳۴، ص ۱۸۷۰–۱۸۷۵٫ [ Google Scholar ]
وو، ایکس. زوریتا میلا، ر. Verdiguier، EI; کراک، ام.-جی. سه خوشه‌بندی سری‌های زمانی جغرافیایی مرجع برای تحلیل الگوهای تغییرپذیری درون سالانه دما. ان صبح. دانشیار Geogr. ۲۰۱۷ ، ۱۰۸ ، ۷۱-۸۷٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ویسر، اچ. اهمیت تغییر آب و هوا در هلند. تجزیه و تحلیل روندهای تاریخی و آینده (۱۹۰۱-۲۰۲۰) در شرایط آب و هوایی، شرایط شدید آب و هوا و تأثیرات مرتبط با دما. MNP Rep. ۲۰۰۵ , ۵۵۰۰۰۲۰۰۷٫ موجود به صورت آنلاین: https://www.pbl.nl/en/publications/The_significance_of_climate_change_in_the_Netherlands (در ۵ ژانویه ۲۰۲۲ قابل دسترسی است).
گارسن، جی. هارمسن، سی. De Beer, J. اثر موج گرمای تابستان ۲۰۰۳ بر مرگ و میر در هلند. Eurosurveillance ۲۰۰۵ ، ۱۰ ، ۱۳-۱۴٫ [ Google Scholar ] [ CrossRef ]
فیشر، PH; مارا، م. Ameling، CB; یانسن، ن. Cassee، FR روند در برآوردهای خطر نسبی برای ارتباط بین آلودگی هوا و مرگ و میر در هلند، ۱۹۹۲-۲۰۰۶٫ محیط زیست Res. ۲۰۱۱ ، ۱۱۱ ، ۹۴-۱۰۰٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
دانیلز، EE; لندرینک، جی. Hutjes، RWA؛ Holtslag، AAM الگوهای بارش فضایی و روند در هلند در طول ۱۹۵۱-۲۰۰۹٫ بین المللی جی. کلیم. ۲۰۱۴ ، ۳۴ ، ۱۷۷۳-۱۷۸۴٫ [ Google Scholar ] [ CrossRef ]
Van Vliet، AJH; Overeem، A.; دی گروت، آر.اس. جیکوبز، AFG; Spieksma، FTM تأثیر دما و تغییرات آب و هوا بر زمان انتشار گرده در هلند. بین المللی جی. کلیم. ۲۰۰۲ ، ۲۲ ، ۱۷۵۷-۱۷۶۷٫ [ Google Scholar ] [ CrossRef ]
Schaap، BF; بلوم-زندسترا، م. هرمانز، CML؛ میربورگ، بی. Verhagen, J. تاثیر تغییرات آب و هوایی شدید بر کشاورزی زراعی در شمال هلند. Reg. محیط زیست چانگ. ۲۰۱۱ ، ۱۱ ، ۷۳۱-۷۴۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شائو، جی. لی، ی. Ni, J. ویژگی های تغییرپذیری دما با زمین، عرض و طول جغرافیایی در منطقه سیچوان-چونگ کینگ. جی. جئوگر. علمی ۲۰۱۲ ، ۲۲ ، ۲۲۳-۲۴۴٫ [ Google Scholar ] [ CrossRef ]
گروبسیچ، TH; وی، آر. موری، AT Spatial Clustering مرور و مقایسه: دقت، حساسیت و هزینه محاسباتی. ان دانشیار صبح. Geogr. ۲۰۱۴ ، ۱۰۴ ، ۱۱۳۴-۱۱۵۶٫ [ Google Scholar ] [ CrossRef ]

شکل ۱٫ خوشه بندی یک طرفه ( a – c )، هم خوشه بندی ( a , d ).

شکل ۲٫ مجموعه داده‌های اسباب‌بازی با نمونه‌های هم‌خوشه‌ای به‌عنوان مقادیر مشابه ( a ) و روندهای مشابه ( b ) که توسط مستطیل‌های چین‌دار ضخیم احاطه شده‌اند.