تجزیه و تحلیل نزدیکترین همسایه
تحلیل نزدیکترین همسایه شامل اندازهگیری فاصله هر ویژگی تا نزدیکترین همسایهاش، سپس مقایسه فواصل مشاهدهشده با فاصلههای مورد انتظار از یک الگوی مکانی تصادفی از ویژگیها است. در ابتدا برای تجزیه و تحلیل توزیع مکانی گونههای گیاهی (کلارک و ایوانز ۱۹۵۴) توسعه داده شد و اکنون یکی از ابزارهای استاندارد GIS برای اندازه گیری الگوهای نقطه است.
تجزیه و تحلیل نزدیکترین همسایه شامل محاسبه نسبت میانگین مشاهده شده و مورد انتظار یا میانگین فاصله بین نقاط و نزدیکترین همسایه آنها برای تولید نزدیکترین آمار همسایه R. فاصله میانگین مورد انتظار از یک الگوی تصادفی از نقاط ، re ، به صورت زیر محاسبه میشود:

در اینجا A اندازه منطقه مورد مطالعه است و n تعداد نقاط است. میانگین فاصله مشاهده شده ، ro به صورت زیر محاسبه میشود :

در اینجا di فاصله بین نقطه ith تا نزدیکترین همسایه است. سپس R به عنوان R = ro/re محاسبه میشود. این مقدار R را در محدوده ۰/۰ الی ۱۴۹۱/۲ میدهد. مقدار R = 0 نشان دهنده خوشه بندی کامل است جایی که همه نقاط اشغال میکنند.
دقیقا در همان مکان بنابراین ، یک الگوی خوشه ای دارای ارزش R به صفر است. هنگامی که یک الگوی منظم پراکنده وجود داشته باشد ، مقدار ۲٫۱۴۹۱ بدست میآید ، که در آن نقاط یک شبکه مثلثی را تشکیل میدهند ، به طوری که هر نقطه دارای فاصله مساوی از شش نزدیکترین همسایه خود و میانگین فاصله تا نزدیکترین همسایه حداکثر میشود. مقدار ۰/۱ یک الگوی تصادفی را نشان میدهد، جایی که میانگین مشاهده شده مساوی با فاصله میانگین مورد انتظار است. قوانین زیر برای توصیف الگوی مکانی با استفاده از R استفاده میشود :
اگر R کوچکتر از یک باشد، آنگاه تمایل به خوشه بندی را نشان میدهد.
اگر R مساوی یک باشد، باشد، یک الگوی تصادفی نشان میدهد.
اگر R بزرگتر از یک باشد، آنگاه تمایل به پراکندگی را نشان میدهد.
با این حال یک مقدار R غیر از ۰/۱ به خودی خود نشان نمیدهد که ویژگیها نوعی ترجیح مکانی دارند و ممکن است تصادفی یا در نتیجه خطای نمونهگیری رخ دهد. احتمال وقوع مقدار R به طور تصادفی از طریق آزمایش اهمیت با استفاده از آمار آزمون z تعیین میشود. H0 بیان میکند که نمونه R به دلیل خطای نمونه برداری یا در نتیجه یک فرایند تصادفی برابر ۰/۱ نیست. آمار آزمون z به صورت زیر محاسبه میشود :

خطای استاندارد کجاست مقدار p مرتبط با نمره az را میتوان برای آزمایش H0 ارزیابی کرد.
به عنوان مثال توزیع قرقاول نشان داده شده در شکل ۵-۴ و ۵-۶ دارای مقدار R 0/500566 است، بنابراین الگوی خوشه ای را نشان میدهد. نمره z برای مقدار R -5/652536 و مقدار p کمتر از ۰۰۰۰۰۱/۰ است. مقدار p نشان میدهد که احتمال به دست آوردن این نمره z بسیار کم است. کمتر از ۰۰۰۰۱/۰ درصد این احتمال وجود دارد که این الگوی خوشه ای ناشی از شانس تصادفی باشد. بنابراین H0 رد میشود و میتوان نتیجه گیری کرد که قرقاولها در حوضه آبریز تمایل به خوشه بندی دارند و این الگوی خوشه ای تصادفی رخ نمیدهد و از نظر آماری معنی دار است.کادر ۵-۵ نمونه دیگری از تجزیه و تحلیل نزدیکترین همسایه از توزیع سرو سرزمین اصلی در حوضه آبریز مجازی را ارائه میدهد.
کادر ۵-۵ تحلیل نزدیکترین همسایه در ArcGIS
کاربردی
برای پیروی از این مثال، ArcMap را شروع کنید و کلاس ویژگی serow را از مسیر زیر بارگیری کنید. serow نشان دهنده توزیع سرزمین اصلی در حوضه مجازی است که مانند شکل ۵-۱۰ نشان داده شده است.
C:\Databases\GIS4EnvSci\VirtualCatchment\Geodata.gdb

شکل ۵-۱۰ توزیع سرو سرزمین اصلی
۱) ArcToolBox را باز کنید. به ابزارهای Spatial Statistics Tools > Analyzing Patterns بروید و سپس روی Average Nearest Neighborدوبار کلیک کنید.
۲) در کادر محاوره ای Average Nearest Neighbor :
الف) serow را به عنوان کلاس ویژگی ورودی انتخاب کنید.
ب) روش فاصله را به عنوان EUCLIDEAN_DISTANCE تنظیم کنید.
ج) برای ایجاد یک خلاصه گرافیکی از نتایج، Generate Report را بررسی کنید.
د) ۴۰۱۷۷۸۳۱۲ را به عنوان اندازه منطقه (که مساحت حوضه آبریز است) وارد کنید.
ه) روی OK کلیک کنید. خلاصههای گرافیکی و متنی از نتایج تولید میشود.
۳) در منوی اصلی، روی Geoprocessing > Results کلیک کنید.
۴) در پنجره نتایج :
الف) Current Session و سپس AverageNearestNeighbor را باز کنید.
ب) روی Report File: NearestNeighbor_Result.html دوبار کلیک کنید. فایل HTML در مرورگر اینترنت پیش فرض باز میشود که خلاصه گرافیکی نتایج را نشان میدهد.
ج) روی Messages در پنجره Results کلیک راست کرده و View را انتخاب کنید. خلاصه متنی از نتایج در یک کادر محاوره ای پیام نمایش داده میشود، همانطور که در شکل ۵٫۱۱ نشان داده شده است. تفسیر از شکل ۵-۱۱ میانگین فاصله مشاهده شده ۳۵/۱۰۳ متر و میانگین فاصله مورد انتظار ۰۶/۱۰۸۷ متر است. R محاسبه شده ۹۵/۰ است که کمتر از ۰/۱ اما نزدیک است. این مقدار نشاندهنده خوشهبندی جزئی در توزیع سروها است. آزمون معناداری منجر به نمره z برابر با ۹۲/۰- شد و مقدار p مرتبط با نمره z 3575/0 است. در سطح معناداری α = ۰۵/۰ ما در رد H0 شکست میخوریم زیرا p-value > α است. میتوان به این نتیجه رسید که الگوی مکانی مشاهده شده میتواند نتیجه یک فرآیند تصادفی یا خطای نمونه گیری باشد و از نظر آماری معنادار نیست. به عبارت دیگر، توزیع سیاره اصلی در ذخیرهگاه الگوی تصادفی را نشان میدهد.
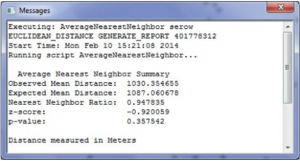
شکل ۵-۱۱ نتایج تحلیل نزدیکترین مجاورت
سه مشکل اصلی در تجزیه و تحلیل نزدیکترین همسایه وجود دارد. اول، آمار R بستگی زیادی به اندازه و شکل منطقه مورد مطالعه دارد. یک ناحیه طولانی و باریک ممکن است مقدار R نسبتاً پایینی را داشته باشد، زیرا نقاط نزدیک به یکدیگر هستند. اگر منطقه مورد مطالعه در مقایسه با میزان توزیع نقطه بزرگ باشد، مقدار R کمی بدست میآید. با این حال اگر همان نقاط به شدت توسط مرز منطقه مورد مطالعه محصور شوند، مقدار R بزرگ تولید میشود. بنابراین با در نظر گرفتن پدیدههای مورد بررسی، مرز باید با دقت ترسیم شود و مقایسه نتایج تجزیه و تحلیل نزدیکترین همسایه زمانی مناسب است که منطقه مورد مطالعه ثابت شود. مشکل دوم این است که همان مقدار R را میتوان از الگوهای نقطه ای بسیار متفاوت به دست آورد، زیرا آماره R فقط به فاصله بین نقاط مربوط میشود.
ترتیب نقاط مانند پیکربندی زاویه ای علاوه بر این آمار فقط الگوی مکانی را از نظر تعداد ویژگیهای فردی در یک منطقه مشخص و عملکرد توزیع فاصله بین آنها توصیف میکند. این تغییرات مکانی در ویژگیهای صفات و خود همبستگی مکانی را نادیده میگیرد.
Global Moran’s I
خود همبستگی مکانی زمانی رخ میدهد که مقادیر متغیر محیطی یا ویژگیهای صفات در مکان به مقادیر متغیر یا ویژگی یکسان در مکانهای نزدیک بستگی داشته باشد. همانطور که در بخش ۵-۴ مورد بحث قرار گرفت، خود همبستگی مکانی حداقل تا حدی در توزیع بسیاری از متغیرها یا ویژگیهای محیطی وجود دارد. شدت همبستگی مکانی ممکن است از مکانی به مکان دیگر و با توجه به جهت متفاوت باشد و انواع الگوهای مکانی را ایجاد کند. هنگامی که مکانهایی با مقادیر مشابه در نزدیکی خوشهها هستند، یا ویژگیهایی با ویژگیهای مشابه در مکان متمرکز میشوند، چنین الگوی مکانی خوشهای به عنوان کل گفته میشود که همبستگی مکانی مثبت را نشان میدهد. هنگامی که مکانهای نزدیک دارای ارزشهای متفاوتی هستند یا ویژگیهای نزدیک به یکدیگر دارای ویژگیهای متفاوت تری نسبت به موارد دورتر هستند که در تقابل با اولین قانون جغرافیایی تولبر است، چنین الگوی مکانی پراکنده خود همبستگی منفی مکانی را به نمایش میگذارد. وقتی ویژگیها یا مقادیر متغیر مستقل از مکان است، الگوی مکانی تصادفی است و هیچ همبستگی خودکار مکانی ندارد.
آمار موران I یکی از معیارهای متداول برای توصیف الگوی مکانی از نظر همبستگی مکانی است (موران، ۱۹۵۰) که به صورت زیر محاسبه میشود :
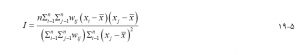
در اینجا n تعداد ویژگیها است، xi مقدار ویژگی ویژگی ith است، مقدار میانگین ویژگی است و wij وزن تعیین کننده همجواری یا مجاورت مکانی بین ویژگیهای i و j است. ماتریس {wij} را ماتریس وزنهای مکانی مینامند. وزنها را میتوان به روشهای مختلف تعریف کرد. آنها را میتوان بر اساس پیوستگی بین ویژگیهای ناحیه یا بر اساس فاصله بین نقاط (ویژگیهای نقطه یا مرکز محورهای ویژگیهای منطقه) تعریف کرد.
وزنهای مکانی مبتنی بر پیوستگی اساساً چنین تعریف میشوند : wij برابر با ۱ است، اگر ویژگیهای i و j به هم نزدیک باشند، یعنی حداقل دارای نقطه مشترک و یا مرز مشترک باشند و در غیر این صورت wij برابر با صفر است. دو نوع مجاورت معمولاً از هم متمایز میشوند : مجاورت مورد ملکه که به ویژگیهایی نیاز دارد تا حداقل یک نقطه مشترک را به اشتراک بگذارند، و مجاورت مورد rook، که به ویژگیها نیاز دارد که حداقل یک مرز مشترک (یا لبه) داشته باشند.
وزنهای مکانی مبتنی بر فاصله به عنوان تابعی از فاصله بین ویژگیها تعریف میشوند. معمولاً آنها به عنوان فاصله معکوس تعریف میشوند :
در اینجا dij فاصله بین ویژگی i و ویژگی j است، و β پارامتر کاهش فاصله است که اغلب به صورت ۱ یا ۲ تنظیم میشود. اوقات، اگر ویژگیهای i و j در یک از پیش تعریف شده باشند، وزنها به سادگی به عنوان wij = 1 تعریف میشوند. فاصله، و wij برابر با صفر اگر دو ویژگی خارج از فاصله از پیش تعریف شده باشند. متناوباً منطقه ای از بی تفاوتی به گونه ای تعریف میشود که wij برابر با یک در صورتی که ویژگیهای i و j در فاصله از پیش تعیین شده قرار داشته باشند و اگر dij بزرگتر از فاصله از پیش تعیین شده است.
وزنهای فضایی مبتنی بر فاصله به عنوان تابعی از فاصله بین ویژگیها تعریف میشوند. معمولاً آنها را به عنوان فاصله معکوس تعریف میکنند: ، که در آن dij فاصله بین ویژگی i و ویژگی j است، و β پارامتر کاهش فاصله است که اغلب به صورت ۱ یا ۲ تنظیم میشود. گاهی اوقات، وزنها به سادگی به عنوان wij برابر با ۱ تعریف میشوند. اگر ویژگیهای i و j در یک فاصله از پیش تعریفشده قرار داشته باشند، و اگر دو ویژگی خارج از فاصله از پیش تعریفشده باشند wij برابر با صفر. به طور متناوب، یک ناحیه بی تفاوتی تعریف میشود به طوری که wij برابر با ۱ اگر ویژگیهای i و j در یک فاصله از پیش تعریف شده باشند و اگر dij بزرگتر از فاصله از پیش تعریف شده باشد.
وزنهای فضایی را نیز میتوان استاندارد کرد. وزنهای استاندارد معمولاً به صورت محاسبه میشوند. به این استانداردسازی ردیف نیز میگویند، زیرا وزنها با تقسیم هر وزن بر مجموع ردیف آن در ماتریس وزنها استاندارد میشوند.
محدوده آماری I موران بین ۱- تا ۱ است. یک الگوی مکانی که خود همبستگی مکانی قوی منفی را نشان میدهد ، مقداری نزدیک به -۱ بدست میآورد ، که بسیار نادر است. مقادیر منفی نشان دهنده خود همبستگی منفی مکانی است که نشان دهنده الگوهای پراکنده است. مقادیر مثبت مربوط به خود همبستگی مکانی مثبت است که نشان دهنده الگوهای خوشه ای است. یک الگوی به شدت خوشهای مقداری نزدیک به ۱ دریافت میکند. مقادیر نزدیک به صفر الگوهای تصادفی را نشان میدهند. قوانین زیر برای توصیف الگوی مکانی با استفاده از I استفاده میشود:
اگر I> 0 باشد ، سپس گرایش به خوشه بندی را نشان میدهد – یعنی مقادیر مشابه تمایل دارند در نزدیکی قرار گیرند.
اگر I = 0 باشد ، سپس یک الگوی تصادفی را نشان میدهد – یعنی مقادیر مستقل از مکان و نامرتبط هستند.
اگر I <0 باشد ، پس گرایش به پراکندگی را نشان میدهد – یعنی مقادیر غیرمتعارف نزدیک یکدیگر قرار دارند.
اهمیت مقدار محاسبه شده موران I با استفاده از آمار آزمون z تحت فرضیه صفر H0 از یک الگوی تصادفی با صفر همبستگی مکانی صفر آزمایش میشود. آمار آزمون z به صورت زیر محاسبه میشود:

در اینجا Ie مورد انتظار است وقتی H0 درست است ، و Iv واریانس I. Ie است، محاسبه میشود:

اگر دادهها از جامعه ای که توزیع آن نرمال است، نمونه برداری شود،

واریانس I عبارت است از: اگر دادهها نمونههای تصادفی از جمعیتی باشند که توزیع آنها ناشناخته است ، واریانس I برابر است با :
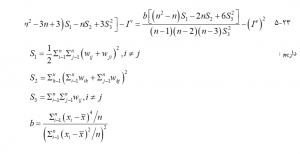
شکل ۵-۱۲ نقشه ای از تراکم جمعیت کهن ( بیشتر و مساوی ۶۵ سال) در کلان شهر ملبورن (واحد منطقه ای منطقه کدپستی است) را نشان میدهد. با اعمال Moran’s I بر روی نقشه و تعریف وزنهای مکانی بر اساس مجاورت مورد روک، با استفاده از ابزار Global Moran’s I در ArcGIS، مقدار Moran’s I 0/72 ، امتیاز az و مقدار p- کمتر از ۰۰۰۰۰۱/۰ تولید کردیم. نتایج نشان میدهد که توزیع جمعیت سالمند الگوی خوشهای با خود همبستگی مکانی کاملاً مثبت را نشان میدهد. با توجه به نمره z 71/19 ، کمتر از ۱ درصد این احتمال وجود دارد که الگوی خوشه ای نتیجه شانس تصادفی باشد. بنابراین H0 مردود است. کادر ۵-۶ از مثال دیگری برای نشان دادن نحوه استفاده از ابزار Global Moran’s I در ArcGIS استفاده میکند، که بر این فرض استوار است که توزیع آماری یک جامعه ناشناخته است و ممکن است توزیع نرمال نباشد. 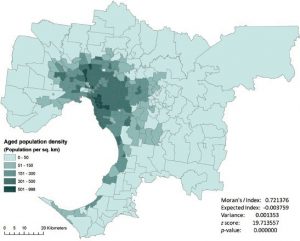
شکل ۵-۱۲ توزیع جمعیت سن در ملبورن و Moran’s
| کادر ۵-۶ Global Moran’s I in ArcGIS |
| مثال |
| برای پیروی از این مثال، ArcMap را شروع کنید و کلاس ویژگی animalDensity را از مسیر زیر بارگیری کنید |
| C:\Databases\GIS4EnvSci\VirtualCatchment\Geodata.gdb |
| یک نقشه شبکه ای است. هر سلول شبکه ۱ کیلومتر × ۱ کیلومتر است، که به عنوان یک ویژگی منطقه با دو ویژگی اصلی نشان داده میشود: تراکم قرقاول (در میدان قرقاول) و تراکم سرو سرزمین اصلی (در میدان سرو). تراکم بر حسب واحد رویت در کیلومتر مربع است. از ضخامت serow landland به عنوان ویژگی برای ساختن نقشه استفاده کنید. باید مانند شکل ۵-۱۳ نشان داده شود. |
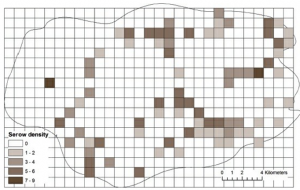
شکل ۵-۱۳ نقشه شبکه چگالی سرو
| ۱) ArcToolBox را باز کنید. به ابزار Spatial Statistics Tools > Analyzing Patterns بروید و روی آدرس زیر دوبار کلیک کنید. |
| Spatial Autocorrelation (Morans I) |
| ۲) در کادر محاورهای Spatial Autocorrelation (Morans I) : |
| الف) animalDensity را به عنوان کلاس ویژگی ورودی انتخاب کنید. |
| ب) serow را به عنوان فیلد ورودی انتخاب کنید. |
| ج) Generate Report را بررسی کنید. |
| د) CONTIGUITY_EDGES_CORNERS را برای مفهومسازی روابط مکانی بین ویژگیها (سلولهای شبکه) انتخاب کنید، یعنی از مجاورت حروف ملکه برای تعریف وزنهای مکانی استفاده کنید. |
| ه) هیچکدام را برای استانداردسازی تنظیم نکنید. |
| و) روی OK کلیک کنید. خلاصههای گرافیکی و متنی از نتایج تولید میشود. |
| ۳) پنجره Results را باز کنید. Current Session را باز کنید، سپس روی Messages کلیک راست کرده و View را انتخاب کنید. خلاصه متنی از نتایج به صورت زیر نمایش داده میشود : |
| Moran′s Index: 0.115993 |
| Expected Index: -0.001919 |
| Variance: 0.000496 |
| z-score: 5.294792 |
| p-value: 0.000000 |
خلاصه گرافیکی نتایج را میتوان با دوبار کلیک کردن بر روی Report File در پنجره Results در جلسه جاری مشاهده کرد. تفسیر ارزش I موران ۰٫۱۱۵۹۹۳ نشان میدهد که توزیع سرزمین اصلی، خودهمبستگی مکانی مثبت ضعیف با الگوی کمی خوشه ای را نشان میدهد، که مشابه نتیجه تحلیل نزدیکترین همسایه است که در کادر ۵-۵ توضیح داده شده است. با این حال، با توجه به امتیاز z 5.294792 و p-value کمتر از ۰٫۰۰۰۰۰۱، احتمال بسیار کمی وجود دارد که این الگو بتواند نتیجه شانس تصادفی باشد. بنابراین، فرضیه صفر الگوی مکانی تصادفی با خودهمبستگی مکانی صفر رد میشود. میتوان به این نتیجه رسید که توزیع سرم سرزمین اصلی تمایل به کمی خوشهبندی دارد، اگرچه مقدار I موران نزدیک به صفر است، که نشاندهنده یک الگوی تصادفی است. این نتیجه گیری کمی متفاوت از تجزیه و تحلیل نزدیکترین همسایه است، که به این نتیجه رسید که الگوی خوشه ای جزئی از نظر آماری معنی دار نیست. همچنین ممکن است سعی کنید از لایه animalDensity برای تجزیه و تحلیل الگوی مکانی قرقاولها با استفاده از آمار Moran’s I بر اساس دادههای تراکم قرقاول با دنبال کردن مراحل بالا استفاده کنید.

