تجزیه و تحلیل الگوهای فضایی
هدف تجزیه و تحلیل الگوی مکانی اندازه گیری میزان خوشه بندی، پراکندگی یا توزیع تصادفی ویژگیها در یک منطقه است. به عنوان مثال آیا تاکینها به طور تصادفی توزیع میشوند، یا در خوشههایی در مناطق خاصی متمرکز میشوند؟ آیا الگوی مکانی گربه پرنده سبز شبیه انجیر خفه کننده است؟ GIS چندین ابزار آماری مکانی ارائه میدهد که نه تنها اندازه گیریهای کمی از الگوی مکانی را ارائه میدهد، بلکه اهمیت آماری آنها را نیز ارزیابی میکند.
آزمایش اهمیت الگوهای فضایی
اهمیت آماری این احتمال است که الگوی مکانی مشاهده شده به احتمال زیاد فقط به دلیل شانس نیست. الگوی مکانی مشاهده شده در صورتی در نظر گرفته میشود که بعید به نظر میرسد به طور اتفاقی رخ داده است. در تجزیه و تحلیل الگوی مکانی بر اساس دادههای نمونه، تعیین اینکه آیا الگوی مکانی کمیسازیشده توسط یک معیار آماری میتواند به تنهایی یا از طریق خطای نمونهگیری به وجود آمده باشد یا اینکه ممکن است به جلوههای آماری معنیدار یک فرآیند مکانی در کار نسبت داده شود، مهم است. این فرآیند را آزمون معناداری یا فرضیه مینامند. اغلب با تعریفی فرضیه صفر و فرضیه جایگزین شروع میشود.
فرضیه صفر H0، موقعیت پیش فرض است که به عنوان مثال، بسته به سؤال تحقیق مورد بررسی، هیچ الگوی مکانی وجود ندارد یا بین دو الگوی مکانی مشاهده شده رابطه وجود ندارد. فرضیه جایگزین، H1 ، موقعیتی مخالف با H0 است. H0 و H1 متقابل هستند و فقط یکی از آنها معتبر تلقی میشود. تحلیل الگوی مکانی اغلب از H0 استفاده میکند که الگوی مکانی مشاهده شده تصادفی است، و H1 که الگوی مکانی مشاهده شده تصادفی نیست. آزمون معناداری یک آزمون آماری خاص را برای یافتن آمار آزمون مشاهده شده و استفاده از آن برای تعیین اینکه آیا H0 باید رد یا پذیرفته شود، اعمال میکند. اگر H0 رد شود، H1 باید پذیرفته شود.
آمار آزمون با تبدیل آمار نمونه (مانند میانگین و انحراف استاندارد) به نمره (مانند نمره z ، F ، t یا χ۲) یافت میشود. چندین آمار آزمون مختلف برای آزمایش انواع مختلف ادعاها استفاده میشود. این بخش فقط آمار آزمون z را مورد بحث قرار میدهد زیرا در تجزیه و تحلیل الگوی مکانی استفاده میشود. آمار آزمون F و t در بخش ۵٫۶ مورد بحث قرار میگیرد. بحث جامع آزمون اهمیت و سایر آمار آزمونها را میتوان در هر کتاب درسی آمار یافت.
از آمار آزمون z یا نمره z برای آزمایش فرضیه صفر در مورد میانگین (یا نسبت) و تعیین اینکه آیا مشاهده (نمونه) میانگین (یا نسبت) مشاهده شده با میانگین (یا نسبت) مورد انتظار جمعیت زیر متفاوت است یا خیر ، استفاده میشود. فرضیه صفر وقتی حجم نمونه بزرگ است (سی یا بیشتر). آماره آزمون z برای میانگین با معادلات زیر بدست میآید :
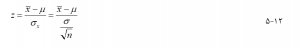
که در آن میانگین مشاهده شده، μ میانگین مورد انتظار، σ انحراف استاندارد جامعه، و n حجم نمونه است. خطای استاندارد میانگین است. بنابراین، هنگام آزمایش فرضیه صفر در مورد میانگین، نمرات z واحدهای انحراف معیار هستند. آمار آزمون z برای نسبت متفاوت محاسبه میشود:

که نسبت مشاهده شده است، p نسبت مورد انتظار است و خطای استاندارد نسبت است.
به عنوان مثال، فرض کنید نمونه ای از ۱۲۰ مزرعه از یک منطقه روستایی داریم که اندازه متوسط آن ۱۳۰ هکتار است. جمعیت مزارع این منطقه به طور متوسط ۶۵ هکتار و انحراف معیار ۱۱۴ هکتار است. H0 این است که بین میانگین نمونه و میانگین جامعه تفاوتی وجود ندارد. امتیاز z برای این مثال :

فرض بر این است که آمار آزمون z دارای توزیع احتمال نرمال است که میتواند به صورت منحنی زنگوله ای به تصویر کشیده شود. همانطور که در شکل ۵-۷ منحنی احتمالات مربوط به نمرات z مختلف را نشان میدهد. زمانی به اوج میرسد که z برابر با صفر است که میانگین توزیع است و دنبالههای آن به محور افقی نزدیک میشوند، اما هرگز به آن نمیرسند. مساحت کل زیر منحنی برابر با ۰/۱ است. نسبت مساحت زیر منحنی بین دو نمره z احتمال قرار گرفتن هر ویژگی یا مقداری بین دو نمره z است. به عنوان مثال مساحت زیر منحنی z بین دو مقدار ۵/۰ و ۵/۰- (همانطور که در آن سایه زده شده است شکل ۵-۷) ۲۹/۳۸ درصد از کل مساحت تحت پوشش منحنی است، بنابراین ۲۹/۳۸ درصد احتمال دارد که هر ویژگی یا مقداری بین دو نمره z قرار گیرد. احتمال رخ ندادن یک ویژگی یا مقدار بین دو امتیاز (یعنی خارج از ناحیه سایه دار) ۱۰۰ درصد از ۲۹/۳۸ درصد برابر با ۷۱/۱۶ درصد است.
احتمالات مرتبط با امتیاز z مبنای تصمیم گیری در مورد رد یا پذیرش فرضیه صفر را تشکیل میدهند. احتمال اتخاذ چنین تصمیمی به عنوان سطح اهمیت شناخته میشود که با α نشان داده میشود. این نیز احتمال اشتباه در رد H0 در واقع معتبر است. گزینههای معمول برای α برابر با ۰۵/۰، ۰۱/۰ و ۱/۰ است که ۰۵/۰ رایج ترین آنها است. نمره z مطلق در سطح اهمیت انتخاب شده را مقدار بحرانی مینامند. مقدار بحرانی مساحت زیر منحنی نرمال آمار آزمون z را به مناطق بحرانی و غیر بحرانی تفکیک میکند (شکل ۵-۸). منطقه بحرانی شامل آمار آزمون است که مقادیر مطلق آن برابر یا بزرگتر از مقدار بحرانی است. هر نمره z در منطقه بحرانی منجر به رد H0 میشود. همه نمرات z در منطقه غیر بحرانی ما را به پذیرش H0 سوق میدهد.
برای مثال قبلی از ۱۲۰ مزرعه در منطقه روستایی، نمره آزمایشی ۲۴۶/۶ فوق العاده زیاد است که در منطقه بحرانی ۰٫۰۱ α = واقع شده است. در واقع احتمال بدست آوردن امتیاز آزمایشی ۲۴۶/۶ کمتر از ۰۰۰۰۰۰۰۰۰۶/۰ است که بسیار کم است. بنابراین میانگین اندازه ۱۳۰ هکتار نمونه مزرعه تفاوت معنی داری با میانگین جمعیت داردکه بسیار بعید است به طور تصادفی رخ دهد و H0 را میتوان با اطمینان رد کرد.
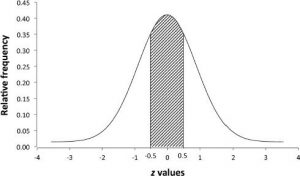
شکل ۵-۷ توزیع آمار آزمون z
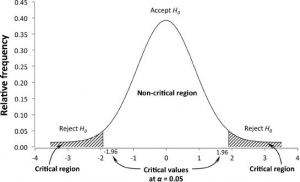
شکل ۵-۸ مقادیر بحرانی و مناطق بحرانی توزیع z
نمرات
احتمال دقیق به دست آوردن مقدار آماره آزمون با قدر معین در صورتی که فرضیه صفر درست باشد، p-value نامیده میشود. مقدار p دو برابر مساحت ناحیه افراطی (منطقه دم) است که با نمره آزمون در زیر منحنی نرمال در توزیع احتمال آماره آزمون محدود شده است (شکل ۵٫۹). اگر امتیاز z محاسبهشده برای نمونه دارای مقدار p برابر یا کمتر از سطح معنیداری باشد، H0 باید رد شود. در غیر این صورت، H0 را نمیتوان رد کرد. سطح معنی داری معمولاً قبل از انجام آزمون معناداری مشخص میشود. ابزارهای تحلیل الگوی مکانی در GIS معمولاً مقدار p مربوط به امتیاز z محاسبهشده را گزارش میکنند. فرضیه صفر یک الگوی مکانی تصادفی یا بدون الگوی مکانی را رد کنید اگر مقدار p ≤ α باشد (سطح معناداری، برای مثال ۰٫۰۵). اگر pvalue> α باشد، فرضیه صفر را بپذیرید.
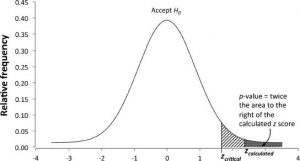
شکل ۵-۹ یافتن مقادیر p در توزیع احتمال نمرات z

