خلاصه
این مقاله بر تجزیه و تحلیل داده‌های بیکاری در چک در یک ساختار فضایی بسیار دقیق و سری‌های زمانی طولانی و سالانه (۲۰۰۲-۲۰۱۹) تمرکز دارد. هدف اصلی این مطالعه بررسی ابعاد فضایی نابرابری‌ها در بیکاری منطقه‌ای و گرایش‌های تکاملی آن در سطح شهرداری بود. برای دستیابی به این هدف از روش های خودهمبستگی فضایی جهانی و محلی استفاده شد. علاوه بر تحلیل‌های مکانی و فضا-زمان، توجه ویژه‌ای به انتخاب ماتریس وزن فضایی داده شد. وزن‌های فضایی با توجه به دسترسی‌های بی‌درنگ بین شهرداری‌ها بر اساس شبکه جاده چک ایجاد شد. نتایج تحلیل‌های خودهمبستگی فضایی بر اساس وزن‌های فضایی شبکه با وزن‌های فضایی مبتنی بر فاصله سنتی مقایسه شد. علی‌رغم تفاوت‌های روش‌شناختی قابل‌توجهی بین وزن‌های فضایی کاربردی، الگوی فضایی حاصل از بیکاری بسیار مشابه بود. از نظر تجربی، ثبات نسبی الگوهای فضایی بیکاری تنها با تغییر آهسته تمایز از سطوح کلان به سطوح خرد قابل مشاهده است.
کلید واژه ها:
نابرابری های اجتماعی و اقتصادی بیکاری ؛ چک _ تحلیل فضا-زمان ؛ دسترسی در زمان واقعی ؛ وزن های فضایی
۱٫ معرفی
بسیاری از اقتصاددانان اخیراً در تحقیقات خود بر تأثیرات فضا و فضایی تأکید کرده اند [ ۱ ، ۲ ]. بیش از پیش، بهبود پیاده‌سازی علم اطلاعات جغرافیایی (GIScience) و درک روش‌های مرتبط با آن حائز اهمیت است. این مقاله نتایج یکی از پدیده‌های اجتماعی-اقتصادی پرمطالعه در علوم اجتماعی و اقتصاد یعنی بیکاری را با استفاده از روش‌های GIS و فضایی تفسیر می‌کند. به دلیل پیچیدگی و دسترسی بالا در مقیاس خرد [ ۳ ، ۴ ، ۵ ]، بیکاری یک موضوع مهم در بین رشته ها است و GIS می تواند بینش های زیادی را ارائه دهد [ ۶ ، ۷ ].
مطالعات بیکاری مورد توجه بسیاری از جامعه شناسان، اقتصاددانان و جغرافیدانان قرار گرفته است. در این مطالعه بر بعد فضایی بیکاری که با بیکاری منطقه ای و نابرابری های منطقه ای به طور کلی مرتبط است، تمرکز کردیم. جنبه های فضایی بیکاری توسط بسیاری از نویسندگان مورد مطالعه قرار گرفته است، مانند [ ۷ ، ۸ ، ۹ ]. نویسندگانی که بیکاری را مطالعه کرده‌اند، همگی الگوهای منطقه‌ای کاملاً پایداری یافته‌اند که حول معنی‌های بیکاری ملی در نوسان است، اما اغلب دارای برخی نقاط پرت خاص هستند، همانطور که در [ ۸ ، ۱۰ ، ۱۱ ، ۱۲ ، ۱۳ ] و همچنین [ ۱۴ ] نشان داده شده است.]، که به طور خاص چک را مطالعه کرد. این به طور مداوم در سطح بین المللی نیز یافت شده است [ ۱۵ ، ۱۶ ، ۱۷ ، ۱۸ ]. اگرچه توضیحات پشت اینرسی بالای الگوهای فضایی بیکاری توسط نویسنده متفاوت است، ثبات نسبی این الگوها به طور کلی مورد توافق است.
اجماع دیگری را می توان در تجزیه بیکاری به تفاوت بین کشورها و تفاوت بین مناطق در آن کشورها یافت. کارهای تجربی نشان داده اند که تفاوت ها از بین کشورها به داخل کشورها منتقل می شوند [ ۱۹ , ۲۰ , ۲۱ , ۲۲]. اثرات مشابهی را می توان در سطح منطقه ای یافت، با اهمیت تفاوت های درون منطقه ای در مقایسه با جزء بین منطقه ای تمایز کلی. با این حال، تفاوت‌های قابل‌توجهی در مناطق خاصی که دستخوش دگرگونی اجتماعی و/یا اقتصادی چشمگیر هستند، وجود دارد. اروپای مرکزی/شرقی (در این مقاله، به ویژه چک) یکی از مناطقی است که الگوهای فضایی اخیر با این توسعه شکل گرفته است. الگوهای فضایی نسبتاً سریع تثبیت شدند و اخیراً به آرامی در حال تغییر هستند. با این حال، ما هنوز هم می‌توانیم گرایش‌های قابل توجهی را در الگوهای فضایی بیکاری مشاهده کنیم. در چک، حجم وسیعی از ادبیات با تمرکز بر بیکاری و تغییرات آن در طول زمان وجود دارد، مانند [ ۲۳ ، ۲۴ ، ۲۵ ]، ۲۶ ]. اکثر نویسندگان موافقند که ریز تمایز در طول زمان افزایش یافته است، اگرچه این روند بسیار ثابت بوده است. با وجود تحقیقات فراوان در مورد این موضوع، سوالات بی پاسخ بسیاری وجود دارد. مهمتر از همه، اکثر فرضیه ها در یک سری زمانی طولانی تر با داده ها در سطوح دقیق (مانند شهرداری ها) آزمایش نشده اند.
ما بعد فضایی بیکاری در چک را در یک سری منحصر به فرد و بلند مدت بر اساس داده های سالانه از سال ۲۰۰۲ تا ۲۰۱۹ مطالعه کردیم. ما بیکاری را با استفاده از داده های شهرداری، یعنی ۶۲۵۰ واحد تقریباً ۱۲٫۶ کیلومتر مربع بررسی کردیم. این سطح مکانی دقیق ما را قادر می سازد تا از روش های پیچیده تری مانند خودهمبستگی فضایی و تجزیه آنتروپی استفاده کنیم. هنگام تجزیه و تحلیل داده‌های شهری با روش‌های آمار فضایی، وزن‌های فضایی اغلب یک موضوع روش‌شناختی مهم در نظر گرفته می‌شوند، اگرچه ما در مقاله قبلی خود نشان داده‌ایم [ ۲۳ ]] که نقش وزن های فضایی کمی اغراق آمیز است. هنگام مطالعه الگوهای کلی، یک موضوع مهم و معتبر وجود دارد، یعنی تفاوت بین وزن‌های فضایی بر اساس فواصل اقلیدسی و وزن‌های فضایی براساس فواصل شبکه به عنوان تابع زمانی (دسترسی زمانی، زوال فاصله) [ ۲۷ ، ۲۸ ، ۲۹ ] . فاصله شبکه هنگام مطالعه فرآیندهای اجتماعی (از جمله بیکاری) مناسب تر است. علاوه بر این، در زمینه بیکاری، که تا حد زیادی به رفت و آمد وابسته است، درک فاصله ها به عنوان یک تابع زمانی (زمان سفر بین شهرداری ها) مفید است [ ۳۰ ]]. بنابراین، علاوه بر فواصل اقلیدسی، از فواصل شبکه (بر اساس شبکه جاده چک) و نمایش زمان آنها به عنوان یک پروکسی (مدت زمان سفر در فضا) نیز استفاده کردیم. اهمیت تفاوت های وزن فضایی در چنین مجموعه داده ای مورد مطالعه قرار نگرفته است. به طور خاص، وزن‌های فضایی شبکه مبتنی بر دسترسی بلادرنگ اغلب به عنوان یک سوگیری بالقوه ذکر می‌شوند، اما هیچ مدرک تجربی برای این فرضیه وجود ندارد.
این پژوهش دو هدف اصلی داشت. هدف اول شناسایی روندهای بلندمدت در توزیع فضایی بیکاری (بعد فضایی بیکاری) در سطح شهرداری در چک بود. یک تحلیل تجربی طولانی مدت و گسترده از این جزئیات سرزمینی هنوز وجود ندارد. این بینش های جدیدی را در مورد تمایلات تکاملی بیکاری در مکان و زمان به ارمغان می آورد. هدف دوم بررسی اهمیت زمان در هنگام تحلیل بعد فضایی بیکاری در چک بود. ما نتایج تحلیل‌های فضایی را بر اساس فواصل و فواصل اقلیدسی به عنوان تابع زمانی (دسترسی زمانی) مقایسه کردیم که از دیدگاه روش‌شناسی مهم است. همانطور که ما یک متغیر اجتماعی مهم را مطالعه کردیم، نتایج ممکن است پیامدهای سیاستی داشته باشند. بررسی پیامدهای سیاست خارج از محدوده این مطالعه بود،۳۱ ، ۳۲ ].
این مقاله تجربی گرا است، در حالی که برخی از مسائل روش شناختی پیچیده تر برای بهبود درک مقاله برای خوانندگان مورد بحث قرار گرفته است. بر اساس گونه شناسی پاستو و همکاران. [ ۳۳ ]، ما نه تنها با آمار فضایی (سطح ۳) و ترکیبی از روش‌های تحلیلی (سطح ۴) بلکه با مدل‌سازی فضایی که به عنوان سطح ۵ برچسب‌گذاری شده است، کار کردیم. به طور خاص، ما بعد فضایی نابرابری‌های اجتماعی-اقتصادی را مورد مطالعه قرار دادیم (برای اطلاعات نظری بیشتر). بحث و جزئیات روش شناختی، نگاه کنید به [ ۲۳ ، ۳۴ ، ۳۵]). علاوه بر بعد فضایی، مهم است که بعد زمانی را نیز در نظر بگیریم. با توجه به بعد زمانی، ما نه تنها پدیده ها را در زمان مطالعه کردیم، بلکه برای درک فواصل مکانی به عنوان توابع زمانی کار کردیم، یعنی فاصله بین دو شهر به عنوان زمان برای رسیدن از یک شهر به شهر دیگر اندازه گیری می شود.
ارزش افزوده اصلی این مطالعه تجربی گسترده، استفاده از روش‌ها و مدل‌سازی پیچیده GIS است. تحقیقات انجام شده در چک ممکن است در کشورهای دیگر نیز تکرار شود. در نتیجه، ممکن است در سطح بین‌المللی به‌عنوان یکی از ارزش‌های افزوده مهم روش‌شناسی، حساسیت کم آن به تفاوت‌های ساختارهای فضایی در دو یا چند سیستم نسبتاً متفاوت (مانند کشورها) اجرا شود. به طور خاص، در این زمینه، با آزمایش اهمیت وزن‌های فضایی با توجه به نتایج تحلیل‌های فضایی، توجه زیادی به اوزان فضایی داشتیم. ما نه تنها از وزن‌های فضایی مبتنی بر فاصله سنتی استفاده کردیم، بلکه از وزن‌های فضایی شبکه بر اساس دسترسی بلادرنگ استفاده کردیم، که در مطالعات فعلی رایج نیست. به خصوص به دلیل در دسترس نبودن داده ها در سطوح خرد، غیر معمول است، که در آن فاصله سنتی ممکن است متفاوت از مسافت سفر (به دلیل موانع فیزیکی، مرزها و غیره) متمایز شود. در سطوح منطقه ای، مسافت سفر بر اساس مقدار متوسط از کل منطقه است که ممکن است به نتایج دقیق کمتری منجر شود. با این حال، چند نمونه تجربی از این گونه تحقیقات وجود دارد [۱۲ ].
این مقاله در چهار بخش ساختار یافته است: (۱) مقدمه مفاهیم نظری و زمینه تجربی در چک. (۲) روش‌شناسی با توجه ویژه به رویکردهای جدید، مانند وزن‌های فضایی شبکه مبتنی بر دسترسی بلادرنگ. (۳) نتایج حاصل از تجزیه و تحلیل فضا-زمان بیکاری با استفاده از قابلیت دسترسی بلادرنگ. و (۴) نتیجه گیری با اشاره به نتایج اصلی این مطالعه.
۲٫ روش شناسی
در تحقیقات بیکاری منطقه ای، فقط از داده های منطقه ای تجمیع شده اغلب استفاده می شود، مانند مناطق اساسی برای اعمال سیاست های منطقه ای در اتحادیه اروپا، مناطق NUTS 2. با این حال، برای مطالعه جزء درون منطقه ای تمایز و جنبه های فضایی در دامنه کامل آنها، به داده های دقیق تری نیاز است. ما بیکاری را در چک مطالعه کردیم. در تمام تحلیل‌ها، ما از داده‌های شهری در یک سری زمانی طولانی (۲۰۰۲-۲۰۱۹) استفاده کردیم. ما از آمار دفاتر کار در چک استفاده کردیم که تعداد بیکاران را گزارش می کند. در این مطالعه، بیکاری به عنوان سهم افراد بیکار در بین جمعیت فعال اقتصادی (گروه سنی ۱۵ تا ۶۴) تعریف شده است. اطلاعات مربوط به جمعیت فعال اقتصادی در ۳۱ دسامبر هر سال از اداره آمار چک در دسترس است. متاسفانه، داده‌های سالهای ۲۰۱۲ و ۲۰۱۳ در دسترس نبود، زیرا داده‌های آن سال‌ها در سطح شهرداری جمع‌آوری نشده بود. نکته مهم این است که مناطق در کل سری زمانی در سال ۲۰۱۹ برای کنترل تغییرات ساختاری با ساختار منطقه ای تنظیم شدند.
ما از روش‌های خودهمبستگی فضایی و تجزیه آنتروپی برای مطالعه جنبه‌های فضایی بیکاری استفاده کردیم [ ۲۳ ]. خود همبستگی فضایی با I موران [ ۳۶ ، ۳۷ ] و تجزیه آنتروپی با شاخص Theil [ ۳۸ ] نشان داده شد. این دو روش از نظر روش شناختی بسیار مرتبط هستند (برای جزئیات، [ ۲۳]). تجزیه شاخص Theil ما را قادر ساخت تا سهم یک سطح منطقه ای منتخب را در تغییرپذیری کلی (بین شهرداری ها در این مورد) کمی کنیم. بنابراین می‌توانیم تغییر تنوع بین سطوح منطقه‌ای را مطالعه کنیم. ما تغییرات در تغییرپذیری بین مناطق شهرداری‌های دارای اختیارات گسترده (AMEP) و مناطق NUTS 3 را به تنوع بین شهرداری‌های درون این مناطق مورد مطالعه قرار دادیم. خودهمبستگی فضایی اطلاعاتی را در مورد سطح کلی خوشه‌بندی بیکاری (خودهمبستگی فضایی جهانی، موران I ) و بازنمایی فضایی آن در قالب خوشه‌های محلی (نقشه‌های خوشه‌ای شاخص‌های محلی انجمن فضایی (LISA)) اضافه کرد. فرمول های هر دو روش ( تجزیه شاخص موران I و Theil) را می توان به صورت زیر نوشت:
من=�∑من=۱�∑�=۱��من�(�من-�)(��-�)∑من=۱�∑�=۱��من�∑من=۱�(�من-�)۲
تی=(∑�=۱ک������لوگاریتم���)+(∑�=۱ک������∑من=۱���من���لوگاریتم�من���)=تیب+تیدبلیو
که در آن n = تعداد واحدها، i = شاخص برای واحدها، j = شاخص برای مناطق، k = تعداد مناطق، y = میانگین بیکاری، w ij = ماتریس وزن فضایی. علاوه بر این، برای T (شاخص کلی Theil)، T B = جزء بین منطقه ای شاخص Theil و T W = جزء درون منطقه ای شاخص Theil. تجزیه، سهم مؤلفه بین منطقه در شاخص کلی Theil، می تواند به صورت T B /T نوشته شود. در تجزیه Theil، ما از دو سطح منطقه ای استفاده کردیم: ۱۴ ناحیه NUTS 3 و ۲۰۶ AMEP.
برای درک تغییر خودهمبستگی فضایی در طول زمان، از خودهمبستگی فضایی دو متغیره [ ۳۹ ] استفاده کردیم. خودهمبستگی فضایی دو متغیره همبستگی های I موران را در زمان اندازه گیری می کند. به طور خاص، دو متغیره موران I به عنوان یک موران من منظم محاسبه شد ، اما مقادیر یک سال انتخاب شده در هر واحد فضایی (شهرداری) با مقادیر میانگین در محله در یک سال مرجع (تأخیر فضایی) همبستگی داشت. معمولاً دو متغیره Moran’s I برای همبستگی بین یک متغیر و قسمت فضایی متغیر دیگر استفاده می شود. با این حال، این ممکن است جنبه فضایی همبستگی را بیش از حد برآورد کند، که اغلب به دلیل همبستگی در محل است [ ۴۰ ]].
یکی از موضوعاتی که اغلب در ارتباط با استفاده از خودهمبستگی فضایی مورد بحث قرار می گیرد، نمایش فضا، به عنوان مثال، ماتریس وزن فضایی ( w ij ) است. این ماتریس موقعیت و مجاورت واحدهای فضایی را عملیاتی می کند [ ۳۶ ، ۴۱ ]. انتخاب ماتریس وزن فضایی زمانی که الگوهای کلی مورد مطالعه قرار می گیرند، بسیار مهم نیست [ ۲۳ ، ۴۲ ]. با این حال، هنگام مطالعه بیکاری، که به شدت تحت تأثیر رفت و آمد است، استفاده از فواصل شبکه می تواند به طور قابل توجهی نه تنها بر سطوح مطلق Moran’s I بلکه بر الگوهای فضایی آن تأثیر بگذارد. وزن فضایی شبکه در [ ۴۳ و ۴۴ ] استفاده شد]. به منظور تولید وزن‌های فضایی شبکه، باید هر شهرداری را با یک کلاس ویژگی نقطه‌ای مرتبط کنیم که هم مبدا و هم مقصد ویژگی را نشان می‌دهد. برای ایجاد وزن‌های فضایی شبکه، از مسافت سفر (به عنوان تابع زمانی) برای محاسبه وزن بین تمام جفت‌های شهرداری استفاده کردیم. برای بحث عمیق تر در مورد ماتریس های وزن فضایی جغرافیایی، [ ۴۵ ] را ببینید.
در این مطالعه از وزن‌های فضایی مبتنی بر فاصله و وزن‌های فضایی شبکه بر اساس فواصل زمان واقعی بین شهرداری‌ها استفاده شد. یک نقطه به نمایندگی از هر شهرداری در یک مکان خاص انتخاب شده قرار گرفت، که نماینده شهرداری بود (در مقایسه با مراکز اغلب استفاده می شود). این مکان ها از اداره آمار چک در دسترس بود. بنابراین، ما مجبور به استفاده از سانتروئید نبودیم. دسترسی زمانی بر اساس شبکه جاده چک از سال ۲۰۱۱ بود، و زمان دسترسی از [ ۴۶ ، ۴۷ ] ساخته شد.]. استفاده از وزن های فضایی شبکه در تحقیقات بیکاری بسیار نادر است. دلیل آن این است که برای ساخت وزن‌های فضایی شبکه، نیاز به داده‌های نقطه‌ای است و مطالعات بیکاری معمولاً با داده‌های منطقه‌ای همراه است. با این حال، استفاده از وزن های فضایی شبکه در تحقیقات بیکاری را می توان در [ ۱۲ ] یافت. مقایسه وزن های فضایی بر اساس فواصل اقلیدسی و وزن های فضایی شبکه در سیستم منطقه ای چک در جدول ۱ ارائه شده است.. حتی اگر همبستگی قوی بین دو روش در هر سه مشخصه انتخاب شده (درصد اتصال فضایی، میانگین تعداد همسایگان و حداکثر تعداد همسایه ها) وجود داشت، همچنان تفاوت های معنی داری وجود داشت، به ویژه، حداکثر تعداد همسایه ها (در امتداد بزرگراه ها). ). مهم است که در نظر داشته باشید که این شباهت ناشی از یک شبکه جاده ای نسبتاً همگن چک است. وضعیت ممکن است در کشورهایی که شبکه های جاده ای کمتر همگن دارند کاملاً متفاوت باشد.
بزرگترین تفاوت بین فواصل اقلیدسی و فواصل شبکه مبتنی بر زمان (فاصله دسترسی) در موارد فردی مشاهده شد. نمونه‌ای از ناحیه‌ای از واحدهای مجاور که با استفاده از هر دو نوع وزن فضایی محدود شده‌اند در شکل ۱ نشان داده شده است ، که در آن واحدهای مجاور که از فواصل اقلیدسی استفاده می‌کنند با واحدهای همسایه بر اساس دسترسی زمانی مقایسه می‌شوند. نقشه به وضوح تفاوت قابل توجهی را بین وزن‌های فضایی مبتنی بر فاصله که با فواصل اقلیدسی کار می‌کنند و وزن‌های فضایی شبکه بر اساس دسترسی زمانی در یک شبکه واقعی نشان می‌دهد. برای تعیین حدود دسترسی زمانی برای کل چک، [ ۴۸ ] را ببینید]. وزن فضایی شبکه بر تحدید حدود منطقه ای بیشتر در امتداد بزرگراه ها و جاده های مهم تأثیر می گذارد، جایی که میانگین سرعت در مقایسه با دیگران بسیار بیشتر است. بنابراین واحدهای همجوار در طول این جاده ها کشیده شدند. وزن‌های فضایی شبکه می‌تواند به کاهش تعصب اغلب بیان‌شده وزن‌های فضایی فاصله اقلیدسی کمک کند.
۳٫ شواهد تجربی در چک
در این بخش تمامی نتایج تجربی ارائه شده است. دو بخش اصلی وجود دارد. ابتدا، ما نتایج تجزیه شاخص Theil و خودهمبستگی فضایی (Moran’s I ) را با ماتریس وزن فضایی مبتنی بر فاصله با فاصله آستانه ۱۰ کیلومتر نشان می‌دهیم. اهمیت تفاوت ها در طول زمان توسط خودهمبستگی فضایی دو متغیره نشان داده شده است. دوم، ما خودهمبستگی فضایی را با استفاده از وزن‌های فضایی شبکه ارائه می‌کنیم. تمام نتایج در سری زمانی ارائه شده است.
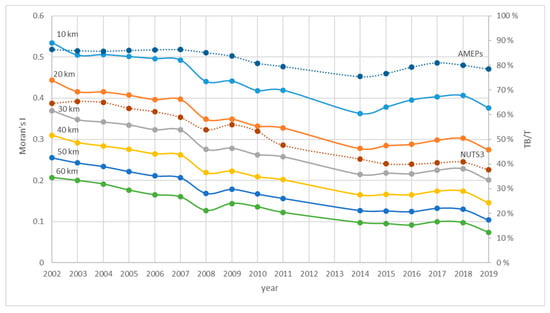
شکل ۲ نتایج تجزیه شاخص Theil را بر روی سطوح AMEP و NUTS 3 و مقادیر Moran’s I برای ماتریس های وزن فضایی با فاصله آستانه ۱۰، ۲۰، ۳۰، ۴۰، ۵۰ و ۶۰ کیلومتر نشان می دهد. از تمام مقادیر، مشهود است که هم سهم مناطق در نابرابری های کلی (تجزیه Theil) و هم خود همبستگی فضایی در طول زمان کاهش یافته است. همچنین این واقعیت را تأیید می کند که تجزیه شاخص Theil و خودهمبستگی فضایی ارتباط نزدیکی دارند [ ۲۳ ]. نکته مهم، کاهش مولفه بین منطقه ای شاخص Theil ( T B / T) نشان می دهد که نابرابری ها از بین مناطق به داخل مناطق تغییر کرده و به سطوح جغرافیایی پایین تر منتقل شده است. در حالی که سهم تغییرپذیری بین منطقه ای در سطح AMEP به طور پیوسته به میزان ۸ درصد (از ۸۶ درصد به ۷۸ درصد) در دوره مورد مطالعه کاهش یافت، در مورد ۲۷ درصد (از ۶۵ درصد به ۳۸ درصد) کاهش یافت. مناطق بزرگتر NUTS 3. این را می توان به عنوان افزایش قابل توجهی در سهم مولفه درون منطقه ای از تنوع (تفاوت بین شهرداری ها در مناطق) تفسیر کرد. گرایش های موران I این یافته را تأیید می کند زیرا سطح کلی خوشه بندی، یعنی تمرکز مقادیر مشابه در فضا، کاهش یافته است.
علاوه بر کاهش پیوسته مقادیر تجزیه شاخص Theil و Moran’s I ، مشاهدات مهم دیگری نیز وجود دارد. داده ها منعکس کننده تغییرات نسبتاً چشمگیر اجتماعی و اقتصادی در این دوره، به ویژه بحران اقتصادی نیستند. با این حال، برخی تغییرات در سال های بحران (۲۰۰۸-۲۰۱۰ در چک) را می توان مشاهده کرد. همانطور که بیکاری کلی در این دوره افزایش یافت، می‌توانیم همگرایی در فلاکت (کاهش نابرابری‌های منطقه‌ای به دلیل شرایط بد کلی) را مشاهده کنیم [ ۵ ]. با این وجود، حتی اگر سطوح مطلق بیکاری در این زمان‌ها تغییر کرد، الگوهای فضایی کلی با تغییرات جزئی ثابت باقی ماندند. این یافته از نتایج سایر نویسندگان حمایت می کند که بیکاری یک متغیر بسیار پایدار با سطح اینرسی بالا است.۳ ، ۱۰ ، ۴۹ ، ۵۰ ].
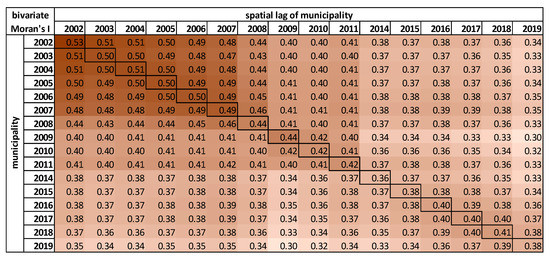
برای آزمایش سیستماتیک تغییر I Moran در طول زمان، ما دو متغیره Moran’s I را محاسبه کردیم . خودهمبستگی فضایی دو متغیره به تعیین کمیت فرض ثبات الگوهای فضایی در طول زمان کمک می کند. در شکل ۳ ، مقادیر مورب مقادیر Moran’s I را در سال های ارائه شده نشان می دهد. مقادیر دیگر در ماتریس نشان دهنده همبستگی I موران در زمان است. به عنوان مثال، اولین مقدار در ستون ۲۰۰۳ (۰٫۵۱) به عنوان Moran’s I محاسبه شد.برای بیکاری در شهرداری ها بر اساس مقادیر سال ۲۰۰۲ بر اساس ساختار فضایی سال مربوطه از ماتریس، در این مورد، ۲۰۰۳٫ بنابراین اولین مقدار در ستون ۲۰۱۹ (۰٫۳۴) نشان دهنده I Moran است که از مقادیر در محاسبه شده است. ۲۰۱۳ بر اساس ساختار فضایی در سال ۲۰۱۹٫ وقتی این مقدار را با مقدار واقعی سال ۲۰۱۹ (۰٫۳۸) مقایسه کردیم، تفاوت به طرز شگفت آوری کم بود. دو متغیره موران I از این یافته حمایت می کند که الگوهای فضایی بیکاری در طول زمان نسبتاً پایدار بوده اند.
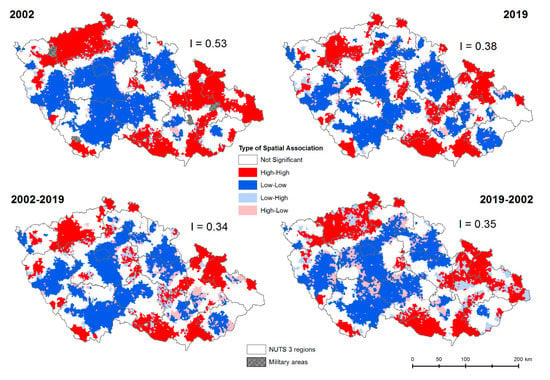
دو متغیر Moran’s I ثبات کلی الگوهای فضایی را در طول زمان در مقیاس جهانی برای تمام چک به تصویر می‌کشد. با این حال، ممکن است برخی از تفاوت های قابل توجهی در سطوح محلی وجود داشته باشد. بنابراین، ما نمایش محلی موران I را به عنوان نقشه های LISA ساختیم ( شکل ۴ را ببینید ). LISA یک نمایش محلی از خوشه بندی فضایی است، در حالی که موران I همبستگی مکانی را از طریق یک مقدار واحد کمی می کند. نقشه‌های خوشه‌ای LISA خوشه‌های فضایی محلی را نشان می‌دهند و به سؤالات مهم پاسخ می‌دهند، مانند اینکه این خوشه‌ها کجا می‌توانند پیدا شوند یا چه شکلی هستند [ ۳۵ ]]. مناطق با خوشه بندی فضایی قابل توجهی از شهرداری ها با مقادیر بالاتر از میانگین (زیر میانگین) بیکاری به عنوان خوشه های بالا- زیاد (کم-کم) تجسم شدند. شهرداری‌هایی که از نظر سطح بیکاری با همسایگی‌شان متفاوت بودند، نقاط پرت فضایی زیاد-کم یا کم-بالا بودند. ما ابتدا و انتهای دوره مورد مطالعه را مقایسه کردیم، یعنی سالهای ۲۰۰۲ و ۲۰۱۹٫ نقشه‌ها به وضوح پایداری نه تنها همبستگی کلی فضایی بلکه الگوهای فضایی در سطح محلی را نیز مستند کردند. مقایسه نشان داد که کدام خوشه ها در طول زمان ثابت مانده اند و کدام مناطق بیشترین تغییر را داشته اند.
تاکنون، همه نتایج بر اساس ماتریس‌های وزن فضایی مبتنی بر فاصله اقلیدسی بودند. در شکل ۵ ، نتایج با وزن های فضایی شبکه بر اساس قابلیت دسترسی بلادرنگ ارائه شده است. نتایج برای آستانه‌های دسترسی زمانی مختلف در فواصل ۵ دقیقه‌ای از فواصل دسترسی ۱۵ تا ۶۰ دقیقه بین شهرداری‌ها مورد آزمایش قرار گرفتند. رفتار Moran’s I برای هر مقدار دسترسی زمانی، الگوی بسیار مشابهی با مقادیر Moran’s I دارد که با آستانه زمانی کاهشی افزایش می‌یابد. این تعجب آور نیست زیرا محله کوچک می شود و خوشه های بیشتری می توانند با کاهش آستانه زمانی تشکیل شوند.
با این حال، کمی تعجب آور است که مقادیر Moran’s I محاسبه شده با استفاده از وزن فضایی فاصله اقلیدسی بسیار شبیه مقادیر Moran’s I محاسبه شده با استفاده از وزن های فضایی شبکه بود (ضریب اسپیرمن ۰٫۹۵؛ ضریب پیرسون ۰٫۹۹). با توجه به اینکه جغرافیای محله برای این دو وزن فضایی کاملاً متفاوت است، این شباهت به ویژه شگفت‌انگیز است ( شکل ۱ را ببینید ). با این حال، تفسیر این نتیجه جالب است. الگوهای فضایی بیکاری را می‌توان تنها با استفاده از وزن‌های فضایی فاصله اقلیدسی، بدون در نظر گرفتن دسترسی زمانی محاسبه کرد. این مهم است زیرا معمولاً داده‌های قابل دسترسی زمانی در دسترس نیستند. این یافته از یافته های [ ۵۱]، که در آن تفاوت بین مناطق اداری و عملکردی بسیار ناچیز بود. با این حال، شباهت نتایج با استفاده از این دو روش نیز تحت تأثیر این واقعیت است که یک شبکه جاده کاملاً متراکم در چک وجود دارد. فرض تشابه این دو وزن فضایی باید برای کشورها/منطقه های مختلف تایید شود.
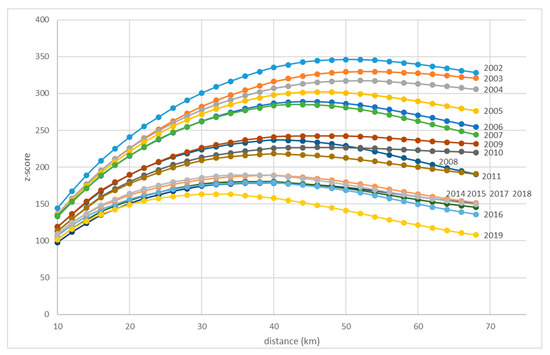
شباهت نتایج برای دسترسی‌های زمانی مختلف را می‌توان با محاسبه سطوح اهمیت z-score برای خودهمبستگی فضایی توضیح داد. پیک های z-score در شکل ۶ نشان می دهد که در کدام فاصله (اقلیدسی) موران Iدر سال های مورد مطالعه بیشترین اهمیت را داشت. در مورد چک، مهم‌ترین مسافت‌ها بسیار بزرگ بودند، حتی اگر در طول زمان کاهش پیدا کردند (۵۰ کیلومتر در سال ۲۰۰۲ در مقابل ۳۵ کیلومتر در سال ۲۰۱۹). هنگام معرفی وزن های فضایی دسترسی زمانی، باید امتیاز z را در نظر گرفت. با این حال، چک برای استفاده از دسترسی‌های زمانی طولانی‌تر بسیار کوچک است، زیرا خوشه‌های فضایی آنقدر بزرگ هستند که امکان تفسیر معنادار را فراهم نمی‌کنند. با این حال، استفاده از z-score و انتخاب سطح دسترسی زمانی مناسب ممکن است زمانی مهم باشد که کشورها یا مناطق مختلف (بزرگتر) مورد مطالعه قرار گیرند.
۴٫ نتیجه گیری
اهداف اصلی این مطالعه (۱) بررسی روندهای بلندمدت در توزیع فضایی بر بیکاری (بعد فضایی بیکاری) و (۲) بررسی تفاوت بین فواصل و فواصل اقلیدسی به عنوان تابع زمانی (دسترسی زمانی، زوال فاصله) بود. . در این بخش، یافته‌های کلیدی روش‌شناختی و تجربی را با برخی بحث در مورد پیامدهای سیاستی آنها ارائه می‌کنیم.
اگرچه استفاده از وزن‌های فضایی شبکه، که به ندرت در زمینه تجربی این مطالعه استفاده می‌شد، به طور قابل توجهی تعریف محله‌ها را تغییر داد (که به مناطق عملکردی ساخته شده با استفاده از داده‌های سفر به محل کار نزدیک‌تر هستند)، الگوی فضایی حاصل از بیکاری بسیار مشابه بود. . این نشان می‌دهد که هنگام مطالعه بیکاری، فواصل اقلیدسی برای محاسبه خوشه‌بندی فضایی با استفاده از روش‌های خودهمبستگی فضایی کافی است. این یک یافته مهم است زیرا داده‌های دسترسی زمانی معمولاً در دسترس نیستند و این مطالعه ثابت کرده است که برای نتایج قوی در شرایط خاص لازم نیست. با این حال، وزن فضایی شبکه ممکن است در مورد متغیرهای متفاوت یا هنگام مطالعه مناطق مختلف با شبکه های جاده ای کم تراکم مهم باشد. با استفاده از وزن های فضایی شبکه، الگوهای فضایی بیکاری از این فرضیه حمایت می کند که برای بیکاری در چک، ساختار منطقه ای با ساختار مناطق عملکردی مطابقت دارد. این با مقایسه تجزیه شاخص Theil (که با مناطق کار می کند) و خودهمبستگی فضایی (که در این مورد با شهرداری ها کار می کند) نشان داده شد. این با یافته های سایر نویسندگان مطابقت دارد.
الگوهای فضایی بیکاری ثابت شد که بسیار پایدار است. آنها تحت تأثیر تغییرات و شوک های اقتصادی و سیاسی (مانند بحران های اقتصادی یا باز شدن مرزها در داخل شینگن) قرار نگرفتند. حتی زمانی که مقادیر مطلق بیکاری به طور قابل توجهی در طول زمان تغییر کرد، الگوهای فضایی نسبتاً پایدار باقی ماندند. با این حال، یک تغییر آهسته و در عین حال ثابت تمایز از سطوح کلان (تغییرپذیری بین مناطق AMEP و NUTS 3) به سطوح خرد (تغییر بین شهرداری‌ها در این مناطق) مشاهده شد. این توسط تجزیه شاخص Theil و همچنین اندازه گیری z-scores Moran’s I مستند شده است . تمام نتایج ذکر شده (ثبات نسبی و تغییر تمایز به سطوح خرد) با نتایج سایر نویسندگان مطابقت دارد.
یافته های تجربی ممکن است پیامدهای سیاست منطقه ای و ملی قابل توجهی داشته باشد. تغییر قابل توجه تنوع از مؤلفه بین منطقه ای به مؤلفه درون منطقه ای نشان می دهد که طرح های مقابله با بیکاری باید از ابزارهای کاهش منطقه ای به ابزارهای خاص محلی در مناطق متمرکز شود. علاوه بر این، ممکن است به مقامات منطقه ای انعطاف بیشتری برای رسیدگی به تفاوت های بین شهرداری ها داده شود. پایداری الگوهای فضایی بیکاری و کاهش نابرابری‌های منطقه‌ای در بحران‌ها (مانند سالهای ۲۰۰۸-۲۰۱۰) نشان می‌دهد که در این زمان‌ها نباید با مناطق مشکل‌ساز رفتار متفاوتی کرد و جنبه‌های منطقه‌ای حمایت دولتی لازم نیست. اولویت متفاوت
در تحقیقات آینده، پیامدهای سیاست مستحق توجه بیشتر است. از دیدگاه روش‌شناسی، وزن‌های فضایی شبکه باید بر روی متغیرهای مختلف آزمایش شوند، زیرا دسترسی زمانی می‌تواند نقش بسیار مهم‌تری ایفا کند. این رویکرد به ویژه در مطالعات مرزی مفید است زیرا مناطق مرزی معمولاً به دلیل زیرساخت های حمل و نقل متراکم کمتر در امتداد مرزها، به ویژه در مورد کشورهایی از هر دو طرف پرده آهنین، تفاوت های بزرگ تری بین فاصله اقلیدسی و فاصله دسترسی زمانی دارند.
منابع
- فینگلتون، بی. López-Bazo، E. مدل های تجربی رشد با اثرات فضایی. پاپ Reg. علمی ۲۰۰۶ ، ۸۵ ، ۱۷۷-۱۹۸٫ [ Google Scholar ] [ CrossRef ]
- Salvati، L. مسائل فضایی: بازسازی قانون اوکون در مقیاس محلی برای ایتالیا. بین المللی J. آخرین روندهای مالی. اقتصاد علمی ۲۰۱۵ ، ۵ ، ۸۳۳-۸۴۰٫ [ Google Scholar ]
- Lewandowska-Gwarda، K. تجزیه و تحلیل فضایی-زمانی نرخ بیکاری در لهستان. Comp. اقتصاد Res. ۲۰۱۲ ، ۱۵ ، ۱۳۳-۱۴۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هورنشتاین، ا. Lubik، TA افزایش بیکاری بلند مدت: علل و پیامدهای بالقوه. اقتصاد Q. ۲۰۱۵ ، ۱۰۱ ، ۱۲۵-۱۴۹٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- نتردووا، پ. بلاژک، جی. افزایش بیکاری در چک در طول بحران اقتصادی جهانی. J. Maps ۲۰۱۹ ، ۱۵ ، ۶۹–۷۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- مویلو، تی. روسانن، جی. ناوکارینن، ا. کولپرت، الف. طول بیکاری به عنوان شاخصی از طرد اجتماعی در فنلاند: دیدگاه GIS. در حاشیه در فضا – گذشته، حال و آینده. جنبه‌های نظری و روش‌شناختی پارامترهای فرهنگی، اجتماعی و اقتصادی مناطق حاشیه‌ای و بحرانی . Jussila, H., Majoral, R., Mutambirwa, CC, Eds.; Routledge: نیویورک، نیویورک، ایالات متحده آمریکا، ۲۰۱۹؛ صص ۱۵۰-۱۶۴٫ [ Google Scholar ]
- Lewandowska-Gwarda، K. رگرسیون وزنی جغرافیایی در تحلیل بیکاری در لهستان. Isprs Int. J. Geo-Inf. ۲۰۱۸ ، ۷ ، ۱۷٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- آراگون، ی. هاتون، دی. هاتون، جی اچ. لکونت، ای. مالین، ای. رویز-گازن، ا. توماس آگنان، سی. توضیح الگوی بیکاری منطقه ای: مورد منطقه میدی پیرنه. پاپ Reg. علمی ۲۰۰۳ ، ۸۲ ، ۱۵۵-۱۷۴٫ [ Google Scholar ] [ CrossRef ]
- الهورست، جی پی راز تفاوت های بیکاری منطقه ای: توضیحات نظری و تجربی. جی. اکون. Surv. ۲۰۰۳ ، ۱۷ ، ۷۰۹-۷۴۸٫ [ Google Scholar ] [ CrossRef ]
- مارتین، آر. نابرابری های بیکاری منطقه ای و پویایی آنها. Reg. گل میخ. ۱۹۹۷ ، ۳۱ ، ۲۳۷-۲۵۲٫ [ Google Scholar ] [ CrossRef ]
- ایوانز، پی. مک کورمیک، بی. الگوی جدید بیکاری منطقه ای: علل و اهمیت سیاست. اقتصاد J. (Land.) ۱۹۹۴ , ۱۰۴ , ۶۳۳-۶۴۷٫ [ Google Scholar ] [ CrossRef ]
- پاتاچینی، ای. Zenou، Y. وابستگی فضایی در نرخ های بیکاری محلی. جی. اکون. Geogr. ۲۰۰۷ ، ۷ ، ۱۶۹-۱۹۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- گرکوسیس، جی. گسترش بیشتر یا پل زدن شکاف؟ مطالعه فرا منطقه ای بیکاری در سراسر اتحادیه اروپا در بحبوحه بحران اقتصادی. پایداری ۲۰۱۸ ، ۱۰ ، ۱۷۰۲٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- مایر، ک. فرانک، دی. روند در قطب بندی فضایی اجتماعی-اقتصادی در جمهوری چک ۲۰۰۱-۲۰۱۱٫ جامعه چک Rev. ۲۰۱۵ , ۵۱ , ۸۹-۱۲۳٫ [ Google Scholar ] [ CrossRef ]
- پهکونن، جی. تروو، اچ. تداوم و گردش مالی در نابرابری های بیکاری منطقه ای. Reg. گل میخ. ۱۹۹۸ ، ۳۲ ، ۴۴۵-۴۵۸٫ [ Google Scholar ] [ CrossRef ]
- نتردووا، پ. نوسک، V. الگوهای فضایی بیکاری در اروپای مرکزی: محورهای توسعه در حال ظهور فراتر از موز آبی. J. Maps ۲۰۱۶ ، ۱۲ ، ۷۰۱–۷۰۶٫ [ Google Scholar ] [ CrossRef ]
- بلاژک، جی. Netrdová، P. اثرات بیکاری منطقه ای بحران مالی جهانی در کشورهای عضو جدید اتحادیه اروپا در اروپای مرکزی و شرقی. یورو مقررات شهری گل میخ. ۲۰۱۲ ، ۱۹ ، ۴۲-۶۱٫ [ Google Scholar ] [ CrossRef ]
- OECD. OECD Employment Outlook 2005 ; انتشارات OECD: پاریس، فرانسه، ۲۰۰۵; صص ۷۳-۱۲۳٫ شابک ۹۲-۶۴-۰۱۰۴۵-۹٫ در دسترس آنلاین: https://img.scoop.co.nz/media/pdfs/0506/OECD.pdf (در ۱۵ ژانویه ۲۰۲۰ قابل دسترسی است).
- Källström, J. مطالعه تجربی همگرایی منطقه ای، نابرابری، و وابستگی فضایی در اتحادیه اروپا بزرگ. پایان نامه کارشناسی ارشد، دانشگاه لوند، لوند، سوئد، آگوست ۲۰۱۲٫ موجود به صورت آنلاین: http://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=3051586&fileOId=3051588 (دسترسی در ۲۰ نوامبر ۲۰۱).
- پوگا، دی. سیاست های منطقه ای اروپا در پرتو نظریه های موقعیت مکانی اخیر. جی. اکون. Geogr. ۲۰۰۲ ، ۲ ، ۳۷۳-۴۰۶٫ [ Google Scholar ] [ CrossRef ]
- دال اربا، س. LeGallo، J. همگرایی منطقه‌ای و تأثیر صندوق‌های ساختاری اروپا در سالهای ۱۹۸۹-۱۹۹۹: یک تحلیل اقتصادسنجی فضایی. پاپ Reg. علمی ۲۰۰۸ ، ۸۷ ، ۲۱۹-۲۴۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- پایک، ا. رودریگز پوز، آ. Tomaney, J. Local and Regional Development , ۲nd ed.; Routledge: لندن، انگلستان، ۲۰۱۶; پ. ۳۸۶٫ ISBN 9781138785724. [ Google Scholar ]
- نتردووا، پ. نوسک، وی. بررسی تنوع و الگوهای جغرافیایی ویژگی های جمعیت: دیدگاه های منطقه ای و فضایی. موراو. Geogr. ۲۰۱۷ ، ۲۵ ، ۸۵-۹۴ . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- بلاژک، جی. Netrdová، P. آیا می توان محورهای توسعه را با متغیرهای اجتماعی-اقتصادی شناسایی کرد؟ مورد چک. Geografie ۲۰۰۹ ، ۱۱۴ ، ۲۴۵-۲۶۲٫ [ Google Scholar ] [ CrossRef ]
- بلاژک، جی. Netrdová، P. گرایش های معاصر توسعه الگوی فضایی در سطح محلی در چک: به سوی تکه تکه شدن بالاتر الگوی فضایی؟ Geografie ۲۰۱۲ ، ۱۱۷ ، ۲۶۶-۲۸۸٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- جورجدا، ش. ترل، ک. بیکاری منطقه ای و سرمایه انسانی در اقتصادهای در حال گذار. اقتصاد ترانزیت ۲۰۰۹ ، ۱۷ ، ۲۴۱-۲۷۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- مورا-گارسیا، آر.-تی. مارتی-سیریکیان، پ. پرز سانچز، آر. Cespedes-Lopez، MF تحلیل مقایسه ای منهتن، اقلیدسی و فاصله های شبکه. چرا فاصله های شبکه برای افراد حرفه ای شهری مفیدتر است؟ بین المللی چند رشته ای. علمی Geoconf. Sgem ۲۰۱۸ ، ۸٫ [ Google Scholar ] [ CrossRef ]
- آپاریسیو، پی. عبدالمجید، م. ریوا، م. Shearmur، R. مقایسه رویکردهای جایگزین برای اندازه گیری دسترسی جغرافیایی خدمات بهداشتی شهری: انواع فاصله و مسائل مربوط به تجمع-خطا. بین المللی J. Health Geogr. ۲۰۰۸ ، ۷ ، ۱-۱۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لو، بی. چارلتون، ام. هریس، پی. فاثرینگهام، رگرسیون وزن‌دار جغرافیایی AS با متریک فاصله غیراقلیدسی: مطالعه موردی با استفاده از داده‌های قیمت خانه لذت‌بخش. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۴ ، ۲۸ ، ۶۶۰-۶۸۱٫ [ Google Scholar ] [ CrossRef ]
- دتانگ-دسندر، سی. Gaigné، C. مدت زمان بیکاری، اندازه شهر، و تنگی بازار کار. Reg. علمی اقتصاد شهری ۲۰۰۹ ، ۳۹ ، ۲۶۶-۲۷۶٫ [ Google Scholar ] [ CrossRef ]
- Cracolici، MF; کوفارو، م. Nijkamp، P. تحلیل فضایی در مورد تفاوت های بیکاری ایتالیا. آمار Methods Appl. ۲۰۰۹ ، ۱۸ ، ۲۷۵-۲۹۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Rios, V. چه چیزی باعث ایجاد نابرابری بیکاری در مناطق اروپایی می شود؟ رویکرد پانل فضایی پویا. Reg. گل میخ. ۲۰۱۷ ، ۵۱ ، ۱۵۹۹-۱۶۱۱٫ [ Google Scholar ] [ CrossRef ]
- Pászto, V. مقدمه ای بر اکتشاف فضایی داده های اقتصادی. در فضای شناسی. کاوش فضایی داده های اقتصادی و روش های تحلیل میان رشته ای ; Pászto, V., Jürgens, C., Tominc, P., Burian, J., Eds. Springer: Cham، سوئیس، ۲۰۲۰؛ صص ۲۳۵-۲۴۲٫ [ Google Scholar ]
- نوسک، وی. Netrdová، P. تمرکز منطقه ای و فضایی پدیده های اجتماعی-اقتصادی: شواهد تجربی از جمهوری چک. Ekon. Časopis ۲۰۱۰ ، ۵۸ ، ۳۴۴-۳۵۹٫ [ Google Scholar ]
- نوسک، وی. Netrdová، P. اندازه گیری جنبه های فضایی متغیر. مقایسه خودهمبستگی فضایی با تجزیه منطقه ای در تحقیقات بین المللی بیکاری. تاریخچه Soc. Res. ۲۰۱۴ ، ۳۹ ، ۲۹۲-۳۱۴٫ [ Google Scholar ] [ CrossRef ]
- Anselin, L. اقتصاد سنجی فضایی: روش ها و مدل ها . Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; پ. ۳۰۰٫ شابک ۹۰-۲۴۷-۳۷۳۵-۴٫ [ Google Scholar ]
- Anselin، L. نشانگرهای محلی انجمن فضایی-LISA. Geogr. مقعدی ۱۹۹۵ ، ۲۷ ، ۹۳-۱۱۵٫ [ Google Scholar ] [ CrossRef ]
- شوراکس، AF; Wan, GH تجزیه فضایی نابرابری. جی. اکون. Geogr. ۲۰۰۵ ، ۵ ، ۵۹-۸۱٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Matkan, AA; شهری، م. Mirzaie, M. Bivariate Moran’s I and LISA to Explore the Crash Risky Locations in Urban Areas. N-Aerus ۲۰۱۳ ، XIV ، ۱-۱۲٫ در دسترس آنلاین: http://n-aerus.net/web/sat/workshops/2013/PDF/N-AERUS14_Matkan_Ali%20Akbar_FINAL.pdf (در ۱۵ ژانویه ۲۰۲۰ قابل دسترسی است).
- Anselin, L. GeoDa Workbook. خودهمبستگی فضایی جهانی (۲) – دو متغیره، دیفرانسیل و EB. ۲۰۱۹٫ در دسترس آنلاین: https://geodacenter.github.io/workbook/5b_global_adv/lab5b.html (در ۱۵ ژانویه ۲۰۲۰ قابل دسترسی است).
- گتیس، ع. Aldstadt, J. ساخت ماتریس وزن های فضایی با استفاده از یک آمار محلی. Geogr. مقعدی ۲۰۰۴ ، ۳۶ ، ۹۰-۱۰۴٫ [ Google Scholar ] [ CrossRef ]
- استاخوویچ، اس. Bijmolt، THA مشخصات مدل‌های فضایی: مطالعه شبیه‌سازی روی ماتریس‌های وزنی. پاپ Reg. علمی ۲۰۰۹ ، ۸۸ ، ۳۸۹-۴۰۸٫ [ Google Scholar ] [ CrossRef ]
- کولاک، HE; میمیس اوغلو، تی. ارباس، YS; Bediroglu، S. تجزیه و تحلیل نقطه داغ بر اساس وزن های فضایی شبکه برای تعیین آمار فضایی تصادفات ترافیکی در Rize، ترکیه. عرب جی. ژئوشی. ۲۰۱۸ ، ۱۱ ، ۱-۱۱٫ [ Google Scholar ] [ CrossRef ]
- Zhang، Y. تجزیه و تحلیل نقطه کانونی الگوی فضایی تصادف بزرگراه بر اساس وزن فضایی شبکه. Cven 658- Civ. مهندس Appl. Gis ۲۰۱۰ ، ۱-۲۱٫ در دسترس آنلاین: https://ceprofs.civil.tamu.edu/folivera/TxAgGIS/Fall2010/Yanru%20Zhang.pdf (دسترسی در ۱۵ ژانویه ۲۰۲۰).
- فیاشی، دی. پارنتی، الف. ماتریس های وزن های فضایی جغرافیایی چقدر قابل اعتماد هستند؟ Reg. توسعه دهنده ۲۰۱۴ ، ۴۰ ، ۵۳-۶۸٫ [ Google Scholar ]
- Hudeček, T. مدل دسترسی به زمان توسط حمل و نقل شخصی. Geografie ۲۰۰۸ ، ۱۱۳ ، ۱۴۰-۱۵۳٫ [ Google Scholar ]
- هودچک، تی. چوران، آر. Kufner, J. دسترسی به پراگ با حمل و نقل جاده ای از ۱۹۲۰ تا ۲۰۲۰٫ Geografie ۲۰۱۱ , ۱۱۶ , ۳۱۷-۳۳۴٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- مارادا، م. Květoň، V. ماترن، تی. استیچ، پ. Hudeček, T. الگوهای دسترسی: مطالعه موردی جمهوری چک. یورو Xxi ۲۰۱۳ ، ۲۳ ، ۶۱-۷۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Farragina، AM; پاستور، F. ذهن شکاف: بیکاری در مناطق جدید اتحادیه اروپا. جی. اکون. Surv. ۲۰۰۸ ، ۲۲ ، ۷۳-۱۱۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هوبر، پی. تحولات بازار کار منطقه ای در حال گذار: بررسی ادبیات تجربی. یورو J. Comp. اقتصاد ۲۰۰۷ ، ۴ ، ۲۶۳-۲۹۸٫ [ Google Scholar ]
- کلاپکا، پ. هالاس، م. نتردووا، پ. نوسک، وی. کارایی واحدهای مساحتی در تحلیل فضایی: ارزیابی عملکرد مناطق عملکردی و اداری. موراو. Geogr. ۲۰۱۶ ، ۲۴ ، ۴۷-۵۹ . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شکل ۱٫ نمونه ای از واحدهای مجاور که با استفاده از فواصل اقلیدسی و دسترسی زمانی مشخص شده اند. منبع: محاسبه خود. توجه: شهرداری منتخب، Soutice، نزدیک به بزرگراه اصلی قرار دارد، جایی که بیشترین تفاوت بین فواصل اقلیدسی و دسترسی زمانی مورد انتظار بود.
شکل ۲٫ تجزیه شاخص Theil و Moran’s I با وزن های فضایی مبتنی بر فاصله ۱۰-۶۰ کیلومتر. بیکاری بین سالهای ۲۰۰۲ و ۲۰۱۹ در چک (سطح شهرداری). توجه: بخش‌های اداری موجود: مناطق (NUTS 3 = 14 واحد) و مناطق شهرداری‌های با اختیارات گسترده (AMEPs = 206 واحد).
شکل ۳٫ دو متغیره موران I ، بیکاری بین سال های ۲۰۰۲ و ۲۰۱۹ در چک (سطح شهرداری، داده های سالانه). منبع: وزارت کار و امور اجتماعی، اداره کار جمهوری چک؛ محاسبه خود توجه: I موران بر اساس وزن های فضایی با فاصله اقلیدسی ثابت برای فاصله آستانه ۱۰ کیلومتر محاسبه می شود. همه مقادیر بر اساس ۹۹۹ جایگشت از نظر آماری در سطح معنی داری ۱ درصد معنی دار هستند. سایه رنگ با سطح خودهمبستگی فضایی مطابقت دارد. مقادیر روی مورب نشان دهنده I تک متغیره موران برای سال های مربوطه است.
شکل ۴٫ نقشه های خوشه ای شاخص های محلی تک متغیره و دو متغیره انجمن فضایی (LISA) برای بیکاری بین سال های ۲۰۰۲ و ۲۰۱۹ در چک (سطح شهرداری). منبع: وزارت کار و امور اجتماعی، اداره کار جمهوری چک؛ محاسبه خود توجه: تمام نقشه های خوشه ای LISA برای وزن های فضایی مبتنی بر فاصله با فاصله اقلیدسی ثابت و فاصله آستانه ۱۰ کیلومتر محاسبه شده است.
شکل ۵٫ موران I با ماتریس وزن فضایی شبکه. بیکاری بین سالهای ۲۰۰۲ و ۲۰۱۹ در چک (سطح شهرداری). منبع: وزارت کار و امور اجتماعی، اداره کار جمهوری چک؛ محاسبه خود
شکل ۶٫ سطوح اهمیت z-score برای خود همبستگی فضایی اندازه‌گیری شده توسط Moran’s I با وزن‌های فضایی مبتنی بر فاصله ۱۰-۶۸ کیلومتر برای بیکاری بین سالهای ۲۰۰۲ و ۲۰۱۹ در چک (سطح شهرداری). منبع: وزارت کار و امور اجتماعی، اداره کار جمهوری چک؛ محاسبه خود
بدون دیدگاه