اقدامات گرایش مرکزی
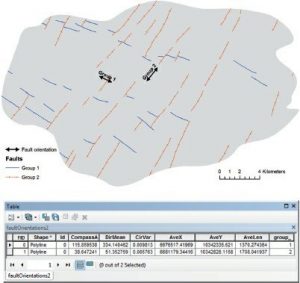
شکل ۵-۳ ابزار جهت خطی گسلهای زمین شناسی
| کادر ۵-۲- اندازه گیری گرایش مرکزی توزیعهای مکانی در ArcGIS |
کاربردی |
| برای پیروی از این مثال ArcMap را شروع کنید و (takin 75) مشاهدات تاکین در سال ۱۹۷۵)۹۵ takin ) مشاهدات تاکین در سال ۱۹۹۵) و خطاها دارای کلاسهایی از مسیر زیر بارگذاری کنید. |
| C:\Databases\GIS4EnvSci\VirtualCatchment\Geodata.gdb. |
مرکز متوسط |
| ۱) ArcToolBox را باز کنید. به ابزارهای آمار مکانی > اندازهگیری توزیعهای جغرافیایی بروید و روی میانگین مرکز دوبار کلیک کنید. |
| ۲) در کادر محاورهای Mean Center |
| الف) Takin75 را به عنوان کلاس ویژگی ورودی انتخاب کنید. |
| ب) کلاس ویژگی خروجی را نام ببرید. |
| ج) روی OK کلیک کنید. لایه نقطه خروجی ایجاد میشود که شامل مرکز میانگین شناسایی شده است. شبیه شکل ۵-۲ a به نظر میرسد. |
| ۳) دو مرحله قبل را برای محاسبه میانگین مرکز برای takin95 تکرار کنید. نتیجه باید مشابه شکل ۵-۲ b باشد. برای تفسیر دو مرکز میانگین به متن مراجعه کنید. |
میانگین خط مستقیم |
| ۴) در ArcToolBox، به Spatial Statistics Tools > Measuring Geographic Distributions بروید و روی Linear Directional Mean دوبار کلیک کنید. |
| ۵) در کادر محاوره ای: Linear Directional Mean |
| الف) خطاها را به عنوان کلاس ویژگی ورودی انتخاب کنید. |
| ب) کلاس ویژگی خروجی را نام ببرید. |
| ج) Orientation Only را تیک بزنید. |
| د) group_ را به عنوان فیلد موردی برای گروه بندی ویژگیها برای محاسبات میانگین جهتی جداگانه انتخاب کنید. فیلد group_ در خطاها شامل دو مقدار ۱ و ۲ است که نشان دهنده دو گروه از خطوط خطا است. گسلهای یک گروه جهت گیری مشابهی دارند. |
| ه) روی OK کلیک کنید. همانطور که در شکل ۵-۳ نشان داده شده است، دو خط در لایه خروجی ایجاد میشود. |
| ۶) روی نام لایه خروجی در فهرست مطالب کلیک راست کرده و جدول ویژگی آن را باز کنید. تفسیر مقادیر صفت نیز در متن آورده شده است. میتوانید ویژگی مرکزی و ابزارهای مرکز میانه را در مجموعه ابزار آمار مکانی با استفاده از مجموعه دادههای مشابه به روشی مشابه امتحان کنید. |
اقدامات پراکندگی
اصله استاندارد و بیضی انحراف استاندارد دو معیار اصلی پراکندگی توزیع مکانی هستند. فاصله استاندارد پراکندگی در مرکز متوسط را اندازه گیری میکند. به صورت زیر محاسبه میشود:
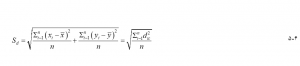
که (،) مختصات مرکز متوسط هستند و dic فاصله از نقطه ith یا centroid تا مرکز متوسط است. بنابراین فاصله استاندارد عبارت از ریشه مربع فاصله میانگین مربع از نقاط یا مرکزها تا مرکز متوسط میباشد. در واحدی که فاصله در آن اندازه گیری میشود بیان میشود. Sd بزرگتر نشان میدهد که ویژگیها گسترده تر هستند. هنگامی که مرکز میانگین وزنی مورد نیاز است، میتوان فاصله استاندارد وزنی را محاسبه کرد :
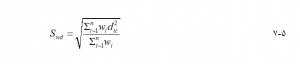
با استفاده از معادله فاصله استاندارد را میتوان برای پاسخ به سوالاتی مانند “کدام گونه قلمرو وسیع تری دارد؟”، “آیا آتش سوزیهای جنگلی در حال حاضر نسبت به ده سال پیش گسترده تر است؟” و “آیا گورالها پراکنده تر از سروها هستند؟” بکار گرفت. در GIS، فاصله استاندارد به صورت دایره در اطراف مرکز متوسط با Sd یا Swd به عنوان شعاع نشان داده میشود. شکل ۵-۴ فواصل استاندارد وزنی توزیع قرقاول را در سه منطقه در حوضه مجازی نشان میدهد که با استفاده از ArcGIS با پیروی از روش نشان داده شده در کادر ۵-۳ محاسبه شده است. وزن تعداد مشاهده است. منطقه ۳ دارای فاصله استاندارد وزنی ۲/۲۳۴۳ متر است که بزرگترین در بین سه منطقه است، بنابراین قرقاولها در این منطقه پراکنده تر از دو منطقه دیگر هستند.
بیضی انحرافی استاندارد روند جهتی یک توزیع مکانی را با محاسبه یک بیضی در مرکز میانگین توزیع اندازه گیری میکند. محور اصلی بیضی جهت حداکثر پراکندگی ویژگیها را نشان میدهد و محور فرعی جهت حداقل پراکندگی را نشان میدهد. مساحت بیضی غلظت ویژگیها را نشان میدهد. زاویه قطب نما محور اصلی θ به صورت زیر محاسبه میشود :
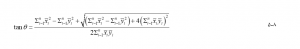
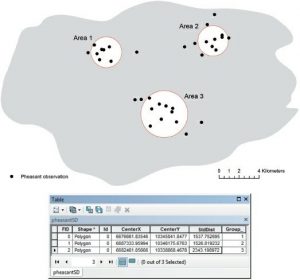 شکل ۵-۴ فواصل استاندارد مشاهدات قرقاول
شکل ۵-۴ فواصل استاندارد مشاهدات قرقاول
در اینجا (،) مختصات مرکز متوسط هستند. θ نشان دهنده جهت توزیع مکانی است. فرمول فوق با تغییر مبدأ سیستم مختصات به مرکز میانگین و سپس چرخاندن آن از طریق تبدیل شباهت (به بخش ۳٫۳ مراجعه کنید) تا حداکثر و حداقل انحراف استاندارد مختصات y تبدیل شده (i = 1, 2, . . . , n) به دست میآیند (شکل ۵-۵). θ زاویه چرخش محور y مربوط به حداکثر انحراف استاندارد است.
با توجه به رابطه ۳-۱ b در بخش ۳-۳، هنگامی که انحراف استاندارد مختصات y تبدیل شده به حداکثر میرسد، انحراف از مرکز میانگین به شرح زیر است:

میانگین مجذور انحرافات بین هر مقدار داده منفرد و میانگین مجموعه داده، واریانس نامیده میشود. انحراف معیار جذر واریانس است (انحراف معیار مهمترین و مفیدترین معیار تغییر مقادیر در مورد میانگین است). بنابراین، حداکثر انحراف استاندارد مختصات y تبدیل شده به صورت زیر است:
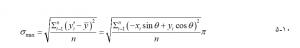
بر این اساس حداقل انحراف استاندارد به شرح زیر محاسبه میشود :
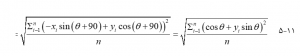
بیضی انحرافی استاندارد توسط σmax به عنوان محور نیمه اصلی، σmin به عنوان محور نیمه جزئی و θ به عنوان جهت محور اصلی تعریف شده است. برای توضیحات کامل ریاضی به (یوئیل، ۱۹۷۱) Yuil مراجعه کنید.
بیضه انحرافی استاندارد اطلاعاتی در مورد پراکندگی ویژگیها و جهت و ناحیه اصلی توزیع آنها ارائه میدهد. مثلا شکل ۵-۶ الگوهای پراکندگی مشاهدات قرقاول را در سه ناحیه مختلف نشان میدهد که در ArcGIS ایجاد شده است. در کادر ۵-۳ مشاهده میشود که سه بیضی در مقایسه با کل منطقه حوضه آبریز کوچک هستند. بدیهی است که توزیع قرقاول خوشه ای است، اما به طور گسترده توزیع نشده است. با استفاده از برخی ابزارهای اندازه گیری GIS و توابع پرسش مکانی، میتوانیم مساحت و تعداد نقاط داده را در هر بیضی محاسبه کنیم، سپس تراکم نقاط داده را در بیضیها محاسبه کنیم. در این مثال تراکم مشاهده قرقاول برای هر بیضی محاسبه میشود. تراکم بیضی در ناحیه ۵۳۱/۱۳ مشاهده/کیلومتر مربع ، بیضی در ناحیه ۲ چگالی ۸۸/۱۶ مشاهده/کیلومتر مربع و چگالی بیضی در ناحیه ۱۴۳/۱۴ مشاهده/کیلومتر مربع است. بنابراین قرقاولها بیشتر در منطقه ۲ متمرکز شده اند. علاوه بر این جهت گیری این بیضیها نشان میدهد که توزیع قرقاول در حوضه آبریز تا حد زیادی تحت تأثیر جریانات رودخانه قرار دارد.
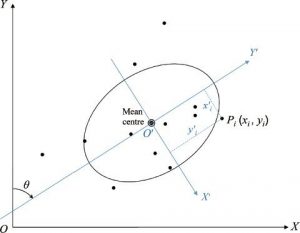
شکل ۵-۵ بیضی انحرافی استاندارد
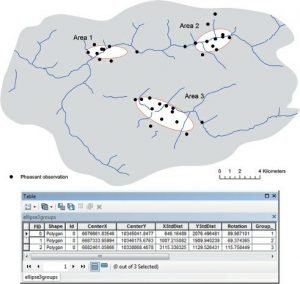
شکل ۵-۶ بیضههای انحرافی استاندارد مشاهدات قرقاول

