کریجینگ
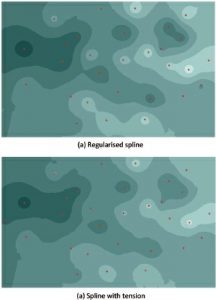
شکل ۴-۳۰ سطوح بارندگی با استفاده از اسپلینها الحاق شدهاند : (الف) اسپلین منظم و (ب) اسپلین با کشش (با استفاده از مجموعه داده یکسان و افسانه مشابه در شکل ۴-۲۷
کریجینگ یک روش زمین آمار برای درون یابی مکانی است. این نام از مهندس معدن آفریقای جنوبی Danie G. Krige گرفته شده است. این تکنیک مشابه IDW است زیرا ارزش یک متغیر را در مکانی بدون نمونه با محاسبه میانگین وزنی از مقادیر شناخته شده نقاط نمونه در همسایگی خود تخمین میزند. با این حال وزن در کریجینگ به تنوع مکانی در مقادیر نقاط نمونه بستگی دارد.
کریجینگ فرض میکند که در بیشتر موارد تغییرات مکانی مشاهده شده در پدیدههای محیطی مانند تغییرات در کیفیت خاک و تغییرات در درجه سنگ معدن، تصادفی و در عین حال از لحاظ مکانی همبستگی دارند و مقادیر دادهها که چنین پدیدههایی را مشخص میکند مطابق با اولین قانون جغرافیای توبلر است (مقادیر داده در مکانهایی که نزدیک یکدیگر هستند عموماً تنوع کمتری نسبت به مقادیر داده در مکانهایی که دورتر از یکدیگر هستند) نشان میدهند. به این حالت خود همبستگی مکانی میگویند. ماهیت دقیق همبستگی خودکار مکانی از مجموعه داده به مجموعه داده دیگر متفاوت است و هر مجموعه داده عملکرد متغیر و فاصله بین نقاط نمونه خاص خود را دارد. این تغییرات توسط Emivariogram نشان داده شده است
یم متغیر نمودار نمودار نیمه متغیر در محور y و فاصله بین نقاط نمونه، به نام تاخیر، در محور x است (شکل ۴-۳۱). نیمه متغیر تنوع مقادیر مشاهده شده را در نقاط نمونه که با فاصله معینی از هم جدا شدهاند اندازه گیری میکند. محاسبه میشود:
![]()
γ (H) نیمه واریانس برای فاصله H است که دو نقطه نمونه را از هم جدا میکند Z (XI) و Z (XI + H)، و N تعداد جفت نقطه نمونه جدا شده توسط H است. به منظور تخمین سالاریا در هر فاصله مشخص، دادههای داده در نیمه متغیریوگرافی با یک منحنی پیوسته نصب میشوند، همانطور که در شکل ۴-۳۱ نشان داده شده است. منحنی ها، که توابع ریاضی به نام مدلهای نیمه متغیریوگرافی نامیده میشوند، میتوانند در اشکال مختلف باشند. شکل ۴-۳۲ برخی از نمونههای مدلهای نیمه متغیریوگرافی را از جمله مدلهای کروی، دایره ای، نمایشی و گاوسی شامل میشود، هر مدل طراحی شده است تا متناسب با انواع مختلف پدیدهها باشد. مدلهای مختلف ممکن است اثرات متفاوتی بر برآورد مقادیر ناشناخته داشته باشند، به ویژه هنگامی که شکل منحنی در نزدیکی مبدا به طور قابل توجهی متفاوت است. مدلها باید بر اساس همبستگی مکانی دادهها و دانش قبلی پدیده انتخاب شوند.
همانطور که در شکل ۴-۳۱ نشان داده شده است، γ (h) انتظار میرود با افزایش فاصله بین دو نقطه داده افزایش یابد. این افزایش معمولاً در فاصله معینی کاهش مییابد که به عنوان محدوده شناخته میشود. فراتر از محدوده، تغییرات در h تأثیر قابل توجهی بر نیمه متغیرها ندارند، بنابراین دیگر هیچ همبستگی خودکار مکانی وجود ندارد. محدوده، مقیاس مکانی را تعیین میکند که در آن دادهها همبستگی دارند. محدودههای کوچکتر نشان میدهد که مقادیر داده با سرعت بیشتری در فضا تغییر میکند. محدوده در کریجینگ برای تعیین اندازه محله استفاده میشود تا نقاط نمونه همبستگی مکانی برای درون یابی انتخاب شوند.
نیمه متغیر در محدوده را آستانه میگویند. اغلب آستانه برابر با واریانس آماری دادهها است. از نظر تئوری در فاصله جداسازی صفر، نیمه متغیر صفر است. با این حال در فاصله جدایی بی نهایت کوچک، نیمه متغیریوگرافی اغلب یک اثر ناگت را نشان میدهد. مقدار قطعه نشان دهنده درجه ای از تصادفی بودن نسبت داده شده به خطاهای اندازه گیری و یا تغییرات مکانی در فواصل کوچکتر از فاصله نمونه برداری است.
کریجینگ از مقادیر نیمهواریانس بهدستآمده از نیمه متغیریوگرافی برازش شده برای تخمین وزنهای مورد استفاده در درونیابی و واریانس مقادیر درونیابی (به عنوان معیاری برای خطاهای پیشبینی) استفاده میکند. اشکال مختلف کریجینگ وجود دارد ( به فصل ۹، بوروق و همکاران، ۲۰۱۵ مراجعه کنید). دو نوع اصلی کریجینگ در زیر معرفی شده است.
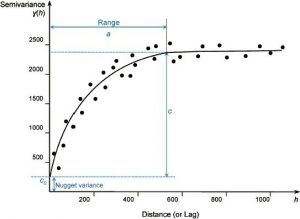
شکل ۴-۳۱ نمونه ای از یک نیم متغیره
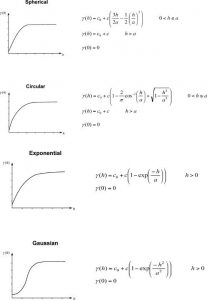
شکل ۴-۳۲ نمونههایی از مدلهای نیمه متغیریوگرافی
کریجینگ معمولی
کریجینگ معمولی فرض میکند که هیچ روندی در دادهها وجود ندارد و میانگین مجموعه داده ناشناخته است. وزنها با حل سیستم معادلات خطی بدست میآیند که واریانس مورد انتظار از دادهها را به حداقل میرساند:
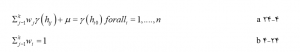
جایی که k تعداد نقاط نمونه در محله است، wi وزن نقطه نمونه ای است که باید تخمین زده شود، γ(hij) نیمه واریانس بین نقاط نمونه i و j است، γ(hi0) نیمه واریانس بین نقطه نمونه i است. و نقطه ای که باید تخمین زده شود و λ ضریب لاگرانژ است که برای اطمینان از حداقل خطای برآورد احتمالی اضافه میشود. هنگامی که wi=(i=1,000,k) مشکل دارد، آنها در معادله ۴-۱۰ برای تخمین ارزشها در مکانهای ناخواسته استفاده میشود.

ریشه مربع واریانس خطای استاندارد را در نقطه درون یابی ارائه میدهد که برآورد خطا و فاصله اطمینان را برای نقطه ناشناخته فراهم میکند. فرض کنید مقدار درون یابی شده z0 باشد. اگر خطاهای درون یابی دارای توزیع نرمال باشد، مقدار واقعی در نقطه درون یابی در داخل با احتمال ۹۵ درصد است. شکل ۴-۳۳ نشان میدهد که سطح بارندگی با استفاده از کریگینگ معمولی در مجموعه دادههای مشابه به عنوان شکل ۴-۲۷ و نقشه خطاهای استاندارد سطح را نشان میدهد.
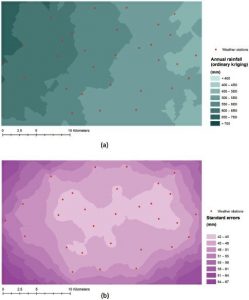
شکل ۴-۳۳ یک سطح بارندگی با استفاده از کریجینگ معمولی و خطاهای استاندارد آن ( با استفاده از مجموعه داده مشابه در شکل ۴-۲۷)
کریجینگ جهانی
کریجینگ جهانی فرض میکند که در دادهها علاوه بر خود همبستگی مکانی بین نقاط نمونه، یک روند غالب وجود دارد و این روند را میتوان با یک تابع چند جمله ای مدل کرد. اگر روند با استفاده از چند جمله ای مرتبه اول تعریف شود داریم :
![]()
سپس وزنهای درون یابی را میتوان با حل مجموعه معادلات همزمان زیر به دست آورد :
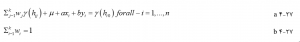
که در آن (xi, yi) مختصات نقطه نمونه i هستند و (x0, y0) مختصات نقطه ای هستند که باید تخمین زده شوند. واریانس برای هر نقطه درون یابی شده توسط :

چندجملههای مرتبه بالاتر را میتوان به شیوه ای مشابه مورد استفاده قرار داد و مجموعه بزرگتری از معادلات همزمان حل شد. شکل ۴-۳۴ سطح بارندگی را که با استفاده از کریجینگ جهانی با روند خطی مرتبه اول و توزیع خطاهای استاندارد آن در هم آمیخته شده نشان میدهد. مطالعه موردی ۸ در فصل ۱۰ نمونه ای از استفاده از کریجینگ جهانی در تجزیه و تحلیل روند آب و هوا را ارائه میدهد.
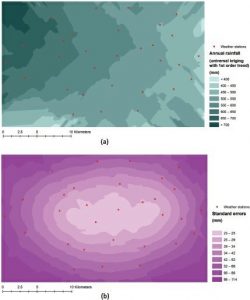
شکل ۴-۳۴ سطح بارندگی با استفاده از کریجینگ جهانی و خطاهای استاندارد آن (با استفاده از مجموعه داده مشابه در شکل ۴-۲۷
در استفاده از کریجینگ، نقاط نمونه بیشتر مدل نیم متغیره دقیق تر تولید میکنند، بنابراین سطح درون یابی دقیق تر است. خطاهای استاندارد به عنوان یکی از خروجیهای کریجینگ، نشان دهنده قابلیت اطمینان مقادیر درون یابی شده است. این ثابت میکند که با شناسایی مکانهایی که نمونههای بیشتری مورد نیاز است، برای بهبود آینده سطح بسیار مفید است. کریجینگ سطحی تولید میکند که از نقاط نمونه عبور میکند. اما مقادیر درون یابی شده به حداکثر و حداقل دادههای نمونه محدود نمیشود.
