با استفاده گسترده از تجهیزات GPS، حجم زیادی از داده های موقعیت مکانی تلفن همراه ثبت می شود و نواحی هات اسپات شهری استخراج شده از داده های GPS می توانند برای خدمات مبتنی بر مکان، مانند توصیه های توریستی و موقعیت یابی نقاط مورد علاقه، اعمال شوند. همچنین می تواند برای تجزیه و تحلیل توزیع مهاجرت جمعیت و استفاده از زمین و برنامه ریزی پشتیبانی تصمیم گیری کند. با این حال، داده های موقعیت مکانی GPS تاکسی دارای مقدار زیادی داده و نقاط پراکنده است. نحوه جلوگیری از تأثیر نویز و شناسایی مؤثر نقاط داغ در شهرها به مشکلات فوری تبدیل شده است که باید حل شود. این مقاله یک الگوریتم خوشه‌بندی را بر اساس نقاط ماندن و چگالی شبکه پیشنهاد می‌کند. در ابتدا، یک الگوریتم پیش پردازش فیلتر با استفاده از طبقه بندی نقاط ماندن و آستانه نقاط ماندن پیشنهاد شده است، بنابراین از تأثیر نقاط توقف اجتناب می شود. سپس، فضای داده به سلول های شبکه مستطیلی تقسیم می شود. هر سلول شبکه به عنوان یک شبکه متراکم یا غیر متراکم با توجه به آستانه چگالی تعریف شده تعیین می شود، و نقاط مرزی خوشه و نقاط نویز در سلول های شبکه غیر متراکم قضاوت می شوند تا از نقاط نمونه برداری معمولی به عنوان نویز تلقی نشود. در نهایت، شبکه های متراکم مرتبط به خوشه ها متصل می شوند. نقاط نمونه برداری نگاشت شده به سلول های شبکه، عناصر موجود در خوشه ها هستند. روش ما کارآمدتر از الگوریتم DBSCAN است زیرا سلول های شبکه محاسبه می شوند. برتری الگوریتم پیشنهادی از نظر دقت خوشه‌بندی و بازده زمانی در مجموعه داده‌های واقعی نسبت به الگوریتم‌های سنتی تأیید می‌شود. هر سلول شبکه به عنوان یک شبکه متراکم یا غیر متراکم با توجه به آستانه چگالی تعریف شده تعیین می شود، و نقاط مرزی خوشه و نقاط نویز در سلول های شبکه غیر متراکم قضاوت می شوند تا از نقاط نمونه برداری معمولی به عنوان نویز تلقی نشود. در نهایت، شبکه های متراکم مرتبط به خوشه ها متصل می شوند. نقاط نمونه برداری نگاشت شده به سلول های شبکه، عناصر موجود در خوشه ها هستند. روش ما کارآمدتر از الگوریتم DBSCAN است زیرا سلول های شبکه محاسبه می شوند. برتری الگوریتم پیشنهادی از نظر دقت خوشه‌بندی و بازده زمانی در مجموعه داده‌های واقعی نسبت به الگوریتم‌های سنتی تأیید می‌شود. هر سلول شبکه به عنوان یک شبکه متراکم یا غیر متراکم با توجه به آستانه چگالی تعریف شده تعیین می شود، و نقاط مرزی خوشه و نقاط نویز در سلول های شبکه غیر متراکم قضاوت می شوند تا از نقاط نمونه برداری معمولی به عنوان نویز تلقی نشود. در نهایت، شبکه های متراکم مرتبط به خوشه ها متصل می شوند. نقاط نمونه برداری نگاشت شده به سلول های شبکه، عناصر موجود در خوشه ها هستند. روش ما کارآمدتر از الگوریتم DBSCAN است زیرا سلول های شبکه محاسبه می شوند. برتری الگوریتم پیشنهادی از نظر دقت خوشه‌بندی و بازده زمانی در مجموعه داده‌های واقعی نسبت به الگوریتم‌های سنتی تأیید می‌شود. شبکه های متراکم مرتبط به خوشه ها متصل می شوند. نقاط نمونه برداری نگاشت شده به سلول های شبکه، عناصر موجود در خوشه ها هستند. روش ما کارآمدتر از الگوریتم DBSCAN است زیرا سلول های شبکه محاسبه می شوند. برتری الگوریتم پیشنهادی از نظر دقت خوشه‌بندی و بازده زمانی در مجموعه داده‌های واقعی نسبت به الگوریتم‌های سنتی تأیید می‌شود. شبکه های متراکم مرتبط به خوشه ها متصل می شوند. نقاط نمونه برداری نگاشت شده به سلول های شبکه، عناصر موجود در خوشه ها هستند. روش ما کارآمدتر از الگوریتم DBSCAN است زیرا سلول های شبکه محاسبه می شوند. برتری الگوریتم پیشنهادی از نظر دقت خوشه‌بندی و بازده زمانی در مجموعه داده‌های واقعی نسبت به الگوریتم‌های سنتی تأیید می‌شود.

کلید واژه ها:

خوشه بندی ; امتیاز اقامت ; چگالی شبکه تشخیص نقاط مهم

۱٫ مقدمه

با توسعه مدیریت شهری پالایش شده و تاکید دولت بر بهبود محیط زندگی و کار، کاربرد عمیق شهرهای هوشمند وارد مرحله جدیدی از توسعه خواهد شد. استخراج مناطق هات اسپات شهری موضوع مهمی در ساخت شهرهای هوشمند است. تغییرات پویا در مناطق کانونی شهری [ ۱ ]، همراه با اطلاعات معنایی کاربری اراضی آن، می تواند برای آشکار کردن عملکرد کاربری زمین شهری استفاده شود [ ۲ ، ۳ ]. انواع مختلفی از حسگرهای GPS اطلاعاتی مانند مختصات طول و عرض جغرافیایی و زمان کاربران تلفن همراه را جمع‌آوری می‌کنند تا مجموعه داده‌های مکان GPS را تشکیل دهند، مانند مکان‌های ورود به شبکه‌های اجتماعی [ ۴ ]، مکان‌های ردیابی ترافیک GPS [ ۵ ]]، مکان‌های ضبط کارت هوشمند [ ۶ ، ۷ ، ۸ ] و مکان‌های تلفن همراه [ ۹ ]، و غیره. برای داده‌های عظیم موقعیت جغرافیایی GPS، یک مدل احتمال مکان ساده [ ۱۰ ] و فناوری تجزیه و تحلیل بصری [ ۱۱ ] برای استخراج خوشه‌های شناسایی نقاط مهم به راحتی تحت تأثیر داده های نویز قرار می گیرد. نحوه برخورد موثر با اطلاعات انبوه داده های مکان هنوز مشکلی است که باید فوراً حل شود.

تحقیقات موجود در مورد استخراج نقاط مهم شهری عمدتاً شامل تشخیص تصاویر ماهواره‌ای با وضوح بالا، شبکه‌های پیچیده و تجزیه و تحلیل آماری است. روش‌های تشخیص ماهواره‌ای سنتی با استفاده از تصاویر ماهواره‌ای با وضوح بالا برای اندازه‌گیری اطلاعات مرتبط در مناطق شهری نیاز به زمان بیشتری دارد [ ۱۲ ]. این روش ها پرهزینه، حرفه ای و برای ترویج و به کارگیری دشوار هستند، بنابراین نمی توانند الزامات به موقع و کم هزینه را برآورده کنند. روش دیگر روش شبکه پیچیده است که عمدتاً از نظریه شبکه های پیچیده برای توصیف و تجزیه و تحلیل اطلاعات هات اسپات استفاده می کند [ ۱۳ ]. برخی از روش های تحلیل آماری و الگوکاوی نیز برای شناسایی نقاط داغ استفاده شده است [ ۱۴ ، ۱۵ ، ۱۶].

استخراج هات اسپات شهری نیز با استفاده از خوشه بندی قابل پیاده سازی است. روش‌های مبتنی بر خوشه‌بندی برای استخراج منطقه کانونی نیازی به مداخله دستی ندارند، که می‌تواند پیچیدگی را ساده‌تر کند. به عنوان مثال، جونگون و همکاران. از تحلیل خوشه‌ای K-means بر روی داده‌های مکان تاکسی‌ها در منطقه ججو برای به دست آوردن نقاط داغ استفاده کرد و نقاط داغ را به رانندگان تاکسی توصیه کرد [ ۱۷ ]. Thuillier و همکاران، بر اساس تعداد زیادی از داده های سوابق تلفن، نقاط داغ شهری را از طریق خوشه بندی به دست آوردند تا نحوه سفر مردم را تعیین کنند [ ۱۸ ]. خوشه بندی یک تکنیک یادگیری ماشینی است که داده ها را گروه بندی می کند [ ۱۹ ]، و به طور گسترده در تشخیص الگو [ ۲۰ ]، پشتیبانی تصمیم [ ۲۱ ]، پردازش تصویر [ ۲۲ ،۲۳ ، ۲۴ ]، داده کاوی [ ۲۵ ]، آزمایش ژنتیکی [ ۲۶ ]، و غیره. اصل اساسی خوشه بندی تقسیم داده های اصلی به چندین ناحیه مجزا بر اساس این اصل است که فاصله بین عناصر در خوشه نسبتاً کم است. و فاصله بین خوشه ها نسبتا زیاد است.

با این حال، الگوریتم خوشه‌بندی شامل تعداد زیادی محاسبات قضاوت فاصله نقطه نمونه‌برداری در هنگام پردازش داده‌های مکان عظیم GPS است که به طور جدی بر عملکرد زمان و کارایی پردازش تأثیر می‌گذارد. علاوه بر این، تجزیه و تحلیل خوشه‌بندی موجود برای مناطق کانونی شهری، عوامل واقعی را ترکیب نمی‌کند. به عنوان مثال، به دلیل سوابق نمونه برداری از راه دور تاکسی ها، نقاط نمونه برداری پراکنده ایجاد می شود. الگوریتم‌های خوشه‌بندی موجود حساس هستند و دقت نتایج خوشه‌بندی تا حد زیادی تحت‌تاثیر نقاط نمونه‌برداری پراکنده قرار می‌گیرد، که ممکن است منجر به تخمین غیرقابل اعتماد مناطق کانونی شهری شود. یک مسئله مهم این است که چگونه می توان تأثیر داده های پر سر و صدا را کاهش داد و دقت خوشه بندی را در حین تکمیل خوشه کاوی کارآمد برای نقاط، بهبود بخشید.

برای حل مشکل روش‌های خوشه‌بندی موجود که کار خوشه‌بندی را به طور کارآمد تکمیل نمی‌کنند و حساسیت آن‌ها به نقاط نویز پراکنده در مجموعه داده‌ها، این مقاله روش‌های خوشه‌بندی را بر اساس نقاط ماندن و تراکم شبکه، از جمله فیلتر کردن نقطه ماندن، نقشه‌برداری شبکه، قضاوت نقطه مرزی پیشنهاد می‌کند. و خوشه بندی شبکه ای متراکم. کمک های خاص به شرح زیر است:

(۱): با توجه به تعداد زیاد نقاط اقامت در مجموعه داده‌های موقعیت تاکسی، این مقاله یک پیش پردازش فیلتر بر اساس طبقه‌بندی نقطه ماندن و آستانه‌های نقطه ماندن را پیشنهاد می‌کند، که می‌تواند از بالا بودن تراکم شبکه در برخی مناطق به دلیل ماندن خودرو جلوگیری کند. مناسبت ها.
(۲): فضای داده موقعیت اصلی در فرآیند نگاشت شبکه و تعیین نقطه مرزی به سلول های شبکه مستطیلی تقسیم می شود، و اینکه آیا هر سلول شبکه یک شبکه متراکم است یا خیر، با توجه به آستانه چگالی تعریف شده تعیین می شود. ما نقاط مرزی خوشه و نقاط نویز را در سلول‌های شبکه غیر متراکم تعیین می‌کنیم تا از شناسایی داده‌های عادی به عنوان نویز جلوگیری کنیم تا داده‌های نویز را با دقت بیشتری پردازش کنیم.
(۳): با توجه به راندمان پایین روش‌های خوشه‌بندی موجود هنگام پردازش مقادیر زیادی داده، این مقاله سلول‌های شبکه متراکم مرتبط را برای تشکیل خوشه‌ها متصل می‌کند. از آنجایی که خوشه‌بندی به سلول‌های شبکه گرایش دارد، نسبت به الگوریتم‌های سنتی کارآمدتر است.
(۴): در نهایت، آزمایش‌ها در مجموعه داده‌های واقعی تأیید می‌کنند که الگوریتم هزینه زمانی خوشه‌بندی را کاهش می‌دهد.

۲٫ آثار مرتبط

در حال حاضر سه نوع روش خوشه‌بندی در تحقیقات داخلی و خارجی وجود دارد: روش‌های تقسیم‌بندی، خوشه‌بندی سلسله مراتبی و خوشه‌بندی چگالی. خوشه‌بندی مبتنی بر تراکم نیازی به تعریف تعداد خوشه‌ها از قبل ندارد و می‌تواند خوشه‌هایی با اشکال مختلف را شناسایی کند که تأثیر خوبی در یافتن مناطق با تراکم بالا دارد. اصل اساسی روش مبتنی بر تراکم این است که وقتی چگالی همسایگی یک نقطه داده از آستانه معینی فراتر رود، به جستجوی همسایگی برای نقاط نمونه گیری در همسایگی ادامه می دهد و در نهایت نقاط داده در یک محدوده نزدیک است. یک خوشه این نوع روش دو پارامتر، حداکثر شعاع ناحیه مجاور و چگالی ناحیه مجاور را تعریف می کند.

خوشه بندی فضایی مبتنی بر چگالی برنامه ها با نویز (DBSCAN) یک الگوریتم کلاسیک مبتنی بر چگالی است. از آنجایی که روش مبتنی بر DBSCAN می تواند به طور دقیق نقاط با چگالی بالا را در مجموعه داده های مکان استخراج کند، به طور موثر در استخراج نقطه ها استفاده می شود. به منظور بررسی تأثیر خوشه بندی بر ساختار شبکه راه [ ۲۷]، Schoier از الگوریتم کلاسیک خوشه‌بندی DBSCAN برای انجام تجزیه و تحلیل خوشه‌ای در منطقه شهری تریست (ایتالیا) استفاده کرد تا ساختار شبکه جاده‌ای را از مناطق “متراکم” نقطه مکان درک کند. با این حال، اینکه آیا نتایج خوشه بندی این الگوریتم برای کاربران واقعی معنادار است یا خیر، به طور سیستماتیک ارزیابی نشده است. در پاسخ به این مشکل، ژو یک الگوریتم خوشه‌بندی مبتنی بر اتصال و چگالی بهبود یافته را برای نقاط مهم استخراج پیشنهاد کرد که برای افراد معنادار است [ ۲۸ ].]، و نویسنده ثابت می کند که نتایج حاصل از الگوریتم با جمع آوری داده های واقعی کاربر معنای عملی دارد، اما این روش فقط اندازه فضایی را در نظر می گیرد و ویژگی های سری زمانی را نادیده می گیرد. هوانگ ویژگی های مکانی-زمانی را در نظر گرفت و از درون یابی خطی برای پر کردن نقاط موقعیتی استفاده کرد که معیارهای اندازه گیری چگالی و مدت زمان مکانی را برآورده نمی کردند. یک الگوریتم خوشه‌بندی فضایی DBSCAN با در نظر گرفتن معیارهای زمانی و فواصل زمانی برای شناسایی نقاط داغ شهری پیشنهاد شد [ ۲۹]. هنگام محاسبه چگالی نقاط GPS، بسیاری از خوشه ها عمدتاً تعداد نقاط GPS در یک فاصله معین را به جای ویژگی های مربوط به آنها در نظر می گیرند. لو و همکاران به جای روش محاسبه چگالی نقطه فعلی در الگوریتم DBSCAN، از یک تابع گاوسی برای اندازه گیری چگالی با تعداد نقاط در فاصله معینی از نقطه فعلی استفاده کرد. یک الگوریتم خوشه‌بندی DBSCAN بر اساس ویژگی‌های ترکیبی پیشنهاد شد [ ۳۰ ] که برای اولین بار مفهوم جدید تحرک را تعریف کرد. منطقه خوشه بندی باید تحرک کمتر و تراکم نقطه GPS بالاتری داشته باشد، هر نقطه مکان تحت تأثیر تعامل با نقاط دیگر قرار می گیرد و می توان نتایج خوشه بندی دقیق تری را به دست آورد.

به عنوان یک فناوری داده کاوی نوظهور، روش های خوشه بندی می توانند از پردازش ماشینی برای جلوگیری از داده های آماری دست و پا گیر و نادرست استفاده کنند. با این حال، روش سنتی خوشه‌بندی مبتنی بر چگالی که در بالا ذکر شد، مستقیماً وظایف خوشه‌بندی را روی نقاط داده انجام می‌دهد. این به تعداد زیادی محاسبات نیاز دارد و در هنگام پردازش مقدار زیادی از داده‌های نقطه نمونه‌برداری مکان، کارایی اجرای الگوریتم پایینی دارد.

برای حل این مشکل می توانیم از خوشه بندی شبکه ای استفاده کنیم. از آنجایی که کل فضای داده با توجه به طول ضلع به سلول های شبکه تقسیم می شود، سلول پردازش شده توسط الگوریتم به جای داده های جداگانه، سلول شبکه تقسیم شده است، بنابراین کارایی خوشه بندی را می توان بهبود بخشید [ ۳۱ ]. در حال حاضر، مطالعاتی با استفاده از الگوریتم‌های خوشه‌بندی چگالی بهینه‌سازی شبکه انجام شده است که می‌تواند کارایی الگوریتم و غربالگری داده‌های نویز پراکنده را بهبود بخشد. از نظر پردازش داده های پر سر و صدا، ژائو و همکاران. یک رشد شبکه و روش خوشه بندی چگالی را بهبود بخشید [ ۳۱]. ناحیه شبکه پراکنده به عنوان داده‌های نویز دور از الگوریتم حذف می‌شود، که توانایی پردازش نویز الگوریتم را افزایش می‌دهد و برای داده‌های مکانی جغرافیایی بزرگ، با مزیت رقابتی در زمان اجرا مناسب است [ ۳۱ ].

با این حال، روش فوق شبکه پراکنده را در هنگام پردازش داده های نویز بیشتر فیلتر نمی کند و شبکه پراکنده ممکن است به عنوان شبکه مرزی خوشه عمل کند. حذف مستقیم بر نتایج خوشه‌بندی تأثیر می‌گذارد و قضاوت داده‌های نویز نادرست است، که ممکن است منجر به مشکل کاهش در دسترس بودن داده شود.

در نهایت، الگوریتم DBSCAN در بالا بهبود یافته است [ ۲۷ ، ۲۸ ، ۲۹] در پردازش، نقاط نمونه برداری در مجموعه داده های تاکسی را در نظر نمی گیرد، که بر دقت روش های خوشه بندی چگالی تأثیر می گذارد. به منظور حل مسائل فوق، این مقاله یک روش خوشه بندی را بر اساس نقاط ماندن و چگالی شبکه پیشنهاد می کند. اولاً، الگوریتم این مقاله مرحله پیش پردازش فیلتر نقطه ماندن را برای کاهش تأثیر نقاط ماندن بر خوشه‌بندی اتخاذ می‌کند. ثانیاً، روش خوشه‌بندی بر اساس نقاط ماندن و چگالی شبکه، نقاط مرزی در سلول شبکه پراکنده را با توجه به آستانه چگالی از پیش تعیین شده قضاوت می‌کند. این روش با انجام ترجمه شبکه ای نقاط مرزی خوشه بندی را بیشتر اصلاح می کند و در نهایت سلول شبکه پراکنده که بخشی از مرز نیست به عنوان داده نویز قضاوت می شود که به قضاوت دقیق تری از داده ها دست می یابد. این روش بر اساس شبکه خوشه بندی می شود،

۳٫ تعاریف مرتبط

ابتدا تعاریف برخی از مفاهیم در این فصل به شرح زیر آورده شده است.

تعریف ۱٫

(سلول شبکه) فرض کنید فضای n بعدی D داده می شود و هر بعد را تقسیم می کنیم

D_{1}, D_{2}, \dots, D_{n}

در فضای D به

m_{1}, m_{2}, m_{3}, \dots m_{n}

; هر یک از سلول های شبکه طول ضلع یکسانی دارند. فضای D به تقسیم می شود

m_{1} * m_{2} * m_{3} * \dots * m_{n}

سلول های شبکه هر سلول شبکه

d_{i}

در فضای D را می توان به صورت زیر بیان کرد.

د من = {د من ۱ ، د من ۲ ، د من ۳, \dots, د من n}

(۱)

جایی که $d_{i_{j}} = [l_{i_{j}}, h_{i_{j}})$ فاصله سلول شبکه است $d_{i}$ در $D_{j}$ بعد و رضایت بخش ۱ ≤ j ≤ n، $l_{i_{j}}, h_{i_{j}}$ نقطه انتهایی چپ و راست بازه هستند و طول بازه طول جانبی سلول شبکه است. از آنجایی که این مقاله در مورد تجزیه و تحلیل خوشه ای از نقاط نمونه برداری توسط داده های موقعیت تاکسی است، منبع داده در اینجا در یک صفحه دو بعدی است، بنابراین بعد فضای مختصات n 2 است و سلول های شبکه را می توان به صورت بصری به عنوان یک شبکه مربع بیان کرد.

تعریف ۲٫

(تراکم سلول های شبکه) پس از تقسیم فضا، تعداد نقاط داده ای که در یک سلول شبکه قرار می گیرند، چگالی سلول شبکه است. اجازه دهید مجموعه نقطه داده ورودی به صورت زیر باشد.

V = {v 1 ، v 2 ، v 3 ، \dots v n}

(۲)

جایی که $v_{i} = \{v_{i}_{1}, v_{i}_{2}, v_{i}_{3}, \dots v_{i}_{n}\}$ ، و $v_{i}_{j}$ جزء نقطه داده است $v_{i}$ در نقطه داده مجموعه V در $D_{j}$ بعد، ابعاد، اندازه. اگر نقطه داده $v_{i}$ در یک سلول شبکه می افتد $d_{i}$ بر روی $D_{j}$ بعد، شرط باید به شرح زیر برآورده شود .

ل من j \leq v من j < ساعت من j, (۱ \leq j \leq n)

(۳)

l_{i_{j}}

h_{i_{j}}

به ترتیب حداقل و حداکثر مقدار بازه هستند. اگر نقطه داده

v_{i}

در یک سلول شبکه می افتد

d_{i}

در n بعد، تعداد تراکم سلول های شبکه یک افزایش می یابد. در مجموعه نقاط نمونه‌برداری مکان دو بعدی، V معمولاً مجموعه‌ای از نقاط طول و عرض جغرافیایی است، بنابراین فقط باید تعیین کرد که آیا هر نقطه نمونه‌برداری در فاصله سلول شبکه مربوطه در دو شاخص طول و عرض جغرافیایی قرار می‌گیرد یا خیر. انجام شمارش تراکم

تعریف ۳٫

(نقطه مرکز شبکه) نقطه مرکزی شبکه به نقطه مرکزی هر سلول شبکه و نقطه مرکزی یک سلول شبکه اشاره دارد. $d_{i}$ به شرح زیر است:

g من d_ج من = (گرم من d_ج من ۱ ، گ من d_ج من ۲ ، گ من d_ج من ۳, \dots, g من d_ج من j ، \dots g من d_ج من n)

(۴)

جایی که $g r i d c_{i}_{j}$ نقطه مرکزی ریاضی سلول شبکه است $d_{i}$ که در $D_{j}$ بعد و فرمول محاسبه آن به شرح زیر است:

g من d_ج من j = ل من j + ساعت من j 2, (۱ \leq j \leq n)

(۵)

جایی که $l_{i_{j}}$ ، $h_{i_{j}}$ به ترتیب حداقل و حداکثر مقدار بازه هستند. از این میان، بعد داده های شبکه در این مقاله دو بعد است، یعنی طول و عرض جغرافیایی. بنابراین، نقطه مرکزی سلول شبکه $d_{i}$ است $g r i d c_{i} = (l o n g i t u d e, l a t i t u d e)$ ، که در آن روش محاسبه طول جغرافیایی میانگین حداقل و حداکثر طول سلول شبکه است. همین امر برای محاسبات عرض جغرافیایی نیز صادق است.

تعریف ۴٫

(نقطه مرکز داده) به موقعیت مرکزی نقاط داده موجود در سلول شبکه اشاره دارد. K نقطه داده در یک سلول شبکه وجود دارد $d_{i}$ بیان شده است $V = \{v_{1}, v_{2}, v_{3}, \dots v_{k}\}$ ، و سپس نقطه مرکز داده سلول شبکه با فرمول (۶) محاسبه می شود.

د a t a ج من = (د a t a ج من ۱ ، د a t a ج من ۲ ، د a t a ج من ۳ ، \dots ، د a t a ج من j ، \dots ، د a t a ج من n)

(۶)

در میان آنها، $d a t a c_{i}_{j}$ مقدار میانگین حسابی مولفه های طرح ریزی شده k نقاط داده V روی بعد Dj است و با فرمول (۷) محاسبه می شود.

د a t a ج من j = v 1 j + v 2 j + v 3 j + \dots + v ک j ک, (۱ \leq j \leq n)

(۷)

با توجه به نقطه مرکزی شبکه در بالا، بعد n استفاده شده در این مقاله دو است، بنابراین نمایش رسمی نقطه مرکز داده همچنان وجود دارد.

d a t a c_{i} = (l o n g i t u d e, l a t i t u d e)

، که در آن روش محاسبه طول جغرافیایی میانگین طول جغرافیایی با تمام نقاط داده در سلول شبکه است و عرض جغرافیایی نیز به همین ترتیب محاسبه می شود.

تعریف ۵٫

(سلول های شبکه ای که مستقیماً مرتبط هستند) دو سلول شبکه حداقل در یک بعد دارای تقاطع هستند و گفته می شود که این دو سلول شبکه مستقیماً به هم مرتبط هستند.

۴٫ روش خوشه بندی بر اساس Stay Point و Grid Density

روش خوشه‌بندی مبتنی بر نقطه ماندن و چگالی شبکه پیشنهادی در این مقاله عمدتاً شامل چهار بخش، یعنی فیلتر کردن نقطه ماندن، نقشه‌برداری شبکه، قضاوت نقطه مرزی و خوشه‌بندی شبکه متراکم است. ابتدا، نقاط ماندن داده های مکان اصلی را شناسایی و فیلتر می کنیم. در این مرحله از رویدادهای تاکسی از پیش تعریف شده و زمان اقامت برای طبقه بندی نقاط اقامت استفاده می شود و آستانه های مختلف نقطه اقامت برای فیلتر مجموعه داده ها استفاده می شود. از طریق آزمایش‌ها، می‌توانیم تنظیمات پارامتر طبقه‌بندی و مقدار آستانه نقطه ماندن را که برای این مجموعه داده اعمال می‌شود، بدست آوریم. در مرحله دوم، نگاشت شبکه بر روی داده های موقعیت فیلتر شده انجام می شود. در این مرحله، طول سلول شبکه از پیش تعیین شده و آستانه چگالی برای تقسیم فضای داده اصلی استفاده می شود و نقاط نمونه برداری موقعیت در شبکه مربوطه برای تعیین مجموعه سلول شبکه متراکم نگاشت می شوند. علاوه بر این، نقاط مرزی خوشه و نقاط نویز را در سلول‌های شبکه غیر متراکم تعیین می‌کنیم. در نهایت، ما از تمام سلول‌های شبکه متراکم مرتبط مستقیماً از خوشه‌های متعدد برای تکمیل خوشه‌بندی شبکه استفاده می‌کنیم.

۴٫۱٫ Stay Point Filtering

در شرایط واقعی، توقف‌های اضافی مانند ماندن در برخی مکان‌ها برای انتظار مهمانان، توقف در تقاطع‌ها و غیره وجود خواهد داشت. با این حال، سنسور موقعیت همچنان به طور مرتب اطلاعات GPS را آپلود می‌کند و در نتیجه نقاط نمونه‌برداری بیش از حد در منطقه ایجاد می‌شود. نقاط ماندن منجر به نتایج خوشه‌بندی نادرست می‌شود. بسیاری از الگوریتم‌های خوشه‌بندی برای تشخیص مناطق کانونی در ادبیات موجود، قضاوت نقاط ماندن را در نظر نمی‌گیرند [ ۲۷ ، ۲۸ ، ۲۹ ]. در پاسخ به این مشکل، این مقاله یک روش پیش تصفیه را برای فیلتر کردن نقطه ثابت پیشنهاد می‌کند.

با توجه به رویدادهای متداول تاکسی و زمان اقامت آنها، این مقاله پنج نوع رویداد اقامت را که در جدول ۱ نشان داده شده است، پیشنهاد می کند . زمان ماندن با ∆t نشان داده می شود. با توجه به رویدادهای اقامت تعریف شده، نقاط اقامت در نقاط نمونه اولیه قابل طبقه بندی و استخراج است.

به دلیل خطاهای دقت در موقعیت یابی GPS، حتی طول و عرض جغرافیایی که دو بار در یک مکان آپلود شده اند ممکن است متفاوت باشد. بنابراین، این مقاله آستانه نقاط ماندن را برای حل این خطای موقعیت‌یابی پیشنهاد می‌کند.

وقتی مقدار آستانه نقطه ماندن از زاویه عرض جغرافیایی ۰٫۰۰۰۱، ۰٫۰۰۱، ۰٫۰۱ باشد، طبق نقشه های شبکه طول و عرض جغرافیایی در سراسر جهان، طول بازه عرض جغرافیایی ۱ درجه برابر است (زیرا طول همه نصف النهارها برابر است) و استاندارد فاصله مربوطه با توجه به طول و عرض جغرافیایی محاسبه می شود. مسافت واقعی مربوطه به ترتیب ۰٫۰۱۱۱ کیلومتر، ۰٫۱۱۱ کیلومتر و ۱٫۱۱ کیلومتر است.

روش پیش پردازش داده ها برای فیلتر انواع مختلف نقاط اقامت مجموعه داده های GPS تاکسی با توجه به رویدادهای اقامت به دنیای واقعی نزدیک تر است. دقت روش بالاتر است، انعطاف پذیری قوی تر است و می توان آن را شخصی کرد. به عنوان مثال، می‌توانیم نقاط نمونه‌برداری با فاصله نمونه‌برداری کمتر از یک دقیقه و طول و عرض جغرافیایی اساساً بدون تغییر از مجموعه داده‌ها استخراج و فیلتر کنیم تا مشکل نتایج خوشه‌بندی نادرست به دلیل تراکم بالای سلول‌های شبکه‌ای که در اثر انتظار ایجاد می‌شود، حل شود. چراغ های راهنمایی

۴٫۲٫ نقشه شبکه

پس از فیلتر کردن مرحله پیش پردازش نقاط اقامت، لازم است نقشه‌برداری شبکه‌ای انجام شود. اندازه شبکه بر نتایج خوشه بندی تأثیر می گذارد. با افزایش اندازه شبکه، دقت کاهش می یابد. تنظیم خاص باید با سناریوی برنامه واقعی ترکیب شود. این مقاله عمدتاً طول شبکه اندازه مربوطه را در ترکیب با مجموعه داده های مختلف تنظیم می کند.

وظیفه اصلی نگاشت شبکه، مش بندی نقاط موقعیت اصلی و محاسبه چگالی سلول شبکه مربوطه است. ابتدا، حداقل نقطه عرض و طول جغرافیایی را در مجموعه داده به عنوان مبدا پیدا می کنیم و سلول شبکه را به کل فضای داده با توجه به طول از پیش تعریف شده سمت سلول شبکه تقسیم می کنیم. در مرحله دوم، تمام شبکه‌ها غربال می‌شوند تا مشخص شود که شبکه‌های متراکم هستند یا خیر. با توجه به مختصات GPS نقاط نمونه برداری اولیه، مشخص می شود که آنها متعلق به کدام شبکه خاص هستند و تعداد نقاط نمونه برداری برای تعیین تراکم سلول شبکه محاسبه می شود. یک سلول یک سلول شبکه متراکم است اگر تعداد نقاط داده در شبکه بیشتر از آستانه چگالی باشد. در غیر این صورت، یک سلول غیر متراکم است.

۴٫۳٫ قضاوت نقطه مرزی

بسیاری از روش های خوشه بندی موجود مستقیماً سلول های غیر متراکم را به عنوان نقاط نویز تنظیم می کنند که باعث می شود بسیاری از نقاط مرزی به عنوان نویز در نظر گرفته شوند و منجر به عدم دقت نتایج خوشه بندی می شود. در این مقاله، سلول‌های شبکه غیر متراکم را برای یافتن داده‌های مرزی خوشه‌ای و داده‌های نویز پراکنده بیشتر اصلاح می‌کنیم.

در این مقاله، فرآیند قضاوت نقطه مرزی سلول های غیر متراکم را به دو نوع تقسیم می کند. یک نوع شبکه غیر متراکم است که هر سلول شبکه متراکم مستقیماً به عنوان یک شبکه متراکم تنظیم می شود. نوع دیگر شبکه هایی هستند که مستقیماً با سلول های متراکم مرتبط نیستند. این مقاله یک روش ترجمه مرکز سلول شبکه ای را پیشنهاد می کند. این روش شبکه‌ای را ترجمه می‌کند که آستانه چگالی را برآورده نمی‌کند و با سلول‌های شبکه متراکم مرتبط نیست. سپس، می‌توانیم نقاط مرزی خوشه و نقاط نویز را با چگالی شبکه جدید تشخیص دهیم.

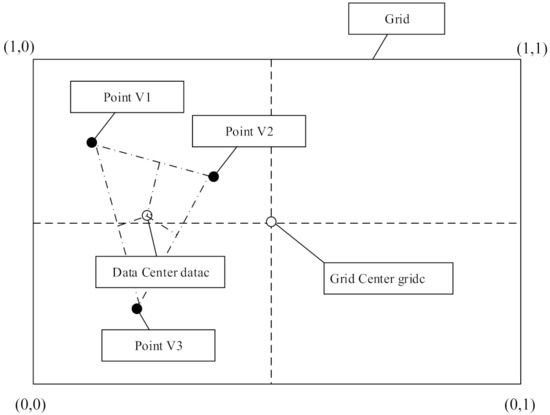
هنگامی که مرکز سلول شبکه جابجا می شود، نقطه مرکز شبکه را به نقطه مرکز داده منتقل می کنیم و طول سمت شبکه را بدون تغییر نگه می داریم. سپس، چگالی سلول های شبکه جدید را دوباره محاسبه می کنیم. اگر مقدار از آستانه چگالی بیشتر باشد، سلول شبکه جدید برای شبکه های متراکم تنظیم می شود. اگر آستانه چگالی هنوز برآورده نشده باشد، سلول شبکه به مجموعه سلول شبکه نویز اضافه می شود. محاسبه مرکز شبکه و نقاط مرکز داده در شکل ۱ نشان داده شده است و فرآیند ترجمه مراکز سلول شبکه در شکل ۲ نشان داده شده است .

در شکل ۱ ، جعبه خط جامد یک سلول شبکه است و چگالی سلول شبکه سه است. سه نقطه نمونه گیری داده وجود دارد. روش محاسبه نقطه مرکزی شبکه [(۰ + ۱)/۲، (۰ + ۱)/۲] = (۰٫۵، ۰٫۵) است. نقطه مرکز داده میانگین مختصات افقی و عمودی سه نقطه نمونه سیاه رنگ داده است.

شکل ۲ روند حرکت سلول شبکه را در این مقاله نشان می دهد. اولاً، سلول شبکه ای که در مرکز شبکه p قرار دارد، شبکه اولیه است. در این زمان، سه نقطه نمونه برداری داده در شبکه وجود دارد و تراکم سلول های شبکه سه است. در فرآیند قضاوت نقاط مرزی، لازم است که مرکز شبکه را به نقطه p’ که نقطه مرکز داده شبکه است منتقل کنید. شبکه جدید ساخته شده در این زمان شامل چهار نقطه نمونه قرمز جدید است، بنابراین تراکم سلول شبکه هفت است.

انتقال مرکز شبکه از نقطه مرکز شبکه به نقطه مرکز داده به شناسایی صحیح شبکه متراکم و جلوگیری از شناسایی نقاط متراکم به عنوان شبکه های پراکنده و حذف آنها کمک می کند. همانطور که در شکل ۲ نشان داده شده است، چگالی اصلی شبکه سه و چگالی پس از حرکت هفت است. اگر آستانه چگالی پنج باشد، فرآیند می تواند از غربالگری نقاط داده در شکل جلوگیری کند.

پس از فرآیند حرکت شبکه فوق، چگالی سلول شبکه جدید را دوباره محاسبه می کنیم. اگر مقدار از آستانه چگالی بیشتر باشد، سلول شبکه جدید روی چگالی تنظیم می شود، در غیر این صورت روی شبکه نویز تنظیم می شود. هنگامی که نقاط مرزی خوشه و نقاط نویز قضاوت می شوند، بنابراین می توانیم تمام نقاط شبکه نویز را به دست آوریم. الگوریتم ۱ مراحل قضاوت نقاط مرزی خوشه را با جزئیات شرح می دهد. نمونه ای از فرآیند اجرای الگوریتم در شکل ۳ نشان داده شده است .

الگوریتم ۱٫ الگوریتم قضاوت مرزی خوشه
ورودی: مجموعه شبکه GS ، آستانه چگالی T
خروجی: مجموعه شبکه فشرده GS’
۱٫	مجموعه شبکه فشرده اولیه GS’
۲٫	برای هر شبکه G در GS
۳٫	اگر چگالی (G) < T
۴٫	اگر G مستقیماً با شبکه فشرده مرتبط باشد
۵٫	G را به GS اضافه کنید
۶٫	در غیر این صورت اجازه دهید مرکز داده مرکز G باشد و شبکه را حرکت دهد
۷٫	اگر چگالی (G) > T
۸٫	G یک شبکه محدود به خوشه است و آن را به GS اضافه کنید
۹٫	دیگر
۱۰٫	G شبکه نویز است و آن را رها کنید
۱۱٫	دیگر
۱۲٫	G را به GS اضافه کنید
۱۳٫	بازگشت GS’

طول ضلع شبکه روی یک و آستانه چگالی در شکل ۳ روی سه تنظیم شده است.. پس از تقسیم سلول های شبکه، طبق اصل بسته شدن و باز کردن سلول های شبکه و آستانه چگالی، قضاوت می شود که شبکه های E و G سلول های شبکه متراکم هستند. از آنجایی که سلول های شبکه B، D، F و H به طور مستقیم با سلول های شبکه متراکم مرتبط هستند، این سلول های شبکه غیر متراکم به عنوان متراکم تنظیم می شوند. سلول های شبکه C، J، A و I بیشتر مشخص می شود که آیا آنها سلول های مرزی خوشه ای هستند یا خیر. همانطور که در کادر قرمز رنگ در شکل نشان داده شده است، نقطه مرکزی سلول شبکه به نقطه مرکز داده منتقل می شود تا یک سلول شبکه جدید ایجاد شود و چگالی شبکه دوباره محاسبه می شود. اگر سلول شبکه جدید آستانه چگالی را برآورده کند، روی سلول شبکه متراکم تنظیم می شود. اگر آستانه چگالی برآورده نشود، نقاط داده در سلول های شبکه اصلی به عنوان “نویز” در نظر گرفته می شوند. سلول شبکه جدیدی که با حرکت سلول شبکه I به دست می آید یک سلول شبکه متراکم است. پس از جابجایی سلول های شبکه غیر متراکم C، J و A، سلول های شبکه جدید آستانه چگالی را برآورده نمی کنند. در نهایت، نقاط داده در این سلول های شبکه غیر متراکم به عنوان داده “نویز” در نظر گرفته می شوند.

۴٫۴٫ خوشه بندی شبکه متراکم

پس از تکمیل قضاوت نقطه مرزی، الگوریتم در این مقاله نیاز به انجام خوشه بندی شبکه ای برای تشکیل خوشه های متعدد دارد. طبق قضاوت مرزی، سلول‌های متراکم و سلول‌های غیر متراکم به دست می‌آیند. سپس، ما باید تمام سلول‌های شبکه‌ای که مستقیماً مرتبط هستند را در یک خوشه جمع کنیم، و نقاط نویز در فرآیند خوشه‌بندی شرکت نمی‌کنند.

فرآیند خوشه‌بندی از روش اول عمق برای یافتن سلول‌های شبکه متراکم مرتبط استفاده می‌کند. ما این سلول های شبکه متراکم مرتبط را در همان مجموعه شبکه ترکیب می کنیم و در نهایت نقاط داده را به خوشه مربوطه نگاشت می کنیم. الگوریتم خوشه بندی شبکه متراکم به عنوان الگوریتم ۲ توصیف می شود.

الگوریتم ۲ از اصل بازگشت برای جستجوی تمام شبکه های غیر خوشه ای با استفاده از پیمایش اول عمق استفاده می کند. ایده اصلی پیمایش اول عمق به شرح زیر است. ابتدا یک راس غیرقابل دسترس را به عنوان راس شروع می گیریم و در امتداد لبه راس فعلی به سمت راس غیرقابل دسترسی حرکت می کنیم. سپس، هنگامی که هیچ رئوسی وجود ندارد که بازدید نشده باشد، به راس قبلی برمی گردیم و به کاوش در سایر رئوس ادامه می دهیم تا همه راس ها بازدید شوند. به طور خلاصه، فرآیند جستجوی عمق ابتدا به این صورت است که در طول یک مسیر تا انتها حرکت کنید، سپس به عقب برگردید، و سپس همان پیاده روی را در مسیر دیگری انجام دهید تا تمام رئوس بازدید شوند.

الگوریتم ۲٫ الگوریتم خوشه بندی شبکه متراکم (DGCA)
ورودی: مجموعه شبکه فشرده GS’ ، شبکه فشرده G
خروجی: مجموعه خوشه ای CS
۱٫	مجموعه کلاستر Init CS
۲٫	برای هر شبکه بدون خوشه G’ در GS’
۳٫	اگر G’ خوشه نباشد و G مستقیماً با G مرتبط باشد
۴٫	G’ را به CS اضافه کنید و G’ را در GS’ حذف کنید
۵٫	DGCA ( GS’ ، G’ )
۶٫	CS را برگردانید

نمونه ای از الگوریتم DGCA در شکل ۴ نشان داده شده است. فرض کنید که پیمایش از واحد شبکه D شروع می شود، شماره خوشه سلول شبکه D یک است و تمام سلول های شبکه قضاوت می شوند، E مستقیماً به آن مرتبط است و شماره خوشه سلول شبکه E یک است. سپس، پیمایش عمیق را با سلول شبکه E ادامه می دهیم. در این زمان، شماره خوشه ای که B به آن تعلق دارد، یک است، واحدهای شبکه ای غیرقابل عبور که مستقیماً با سلول شبکه B مرتبط نیستند، سپس به سلول E باز می گردیم، F مستقیماً با آن مرتبط است و شماره خوشه ای که به آن مربوط می شود. متعلق نیز یکی است; در این زمان، سلول‌های شبکه‌ای که مستقیماً با F مرتبط نیستند و عبور نکرده‌اند، به E برمی‌گردند. بر اساس قیاس، همه سلول‌های شبکه مورد قضاوت قرار می‌گیرند. سلول های شبکه ای G، H و I در خوشه یک وجود دارد. سلول های شبکه ای که خوشه یک را کامل می کنند با شبکه های آبی در شکل مشخص شده اند. نقاط داده در سلول های شبکه A،

۵٫ نتایج تجربی و تجزیه و تحلیل

۵٫۱٫ مجموعه داده ها و محیط تجربی

آزمایش به‌طور تصادفی بخشی از داده‌ها را از مجموعه داده‌های موقعیت درایو T اصلی [ ۳۲ ، ۳۳ ] رهگیری کرد تا چهار مجموعه از داده‌های آزمایشی با مقادیر داده‌های مختلف تولید کند، همانطور که در جدول ۲ نشان داده شده است. مجموعه داده مسیر T-Drive شامل مسیرهای یک هفته ای ۱۰۳۵۷ تاکسی است. تعداد کل نقاط این مجموعه داده حدود ۱۵ میلیون و مسافت کل مسیرها به ۹ میلیون کیلومتر می رسد. در میان آنها، DS1 دو مجموعه از داده های موقعیت تاکسی با شماره های ۷ و ۱۳ است. DS2 چهار مجموعه داده موقعیت تاکسی با شماره های ۳۶، ۳۷، ۱۱۲، ۱۱۴ است. DS3 9 مجموعه داده مکان تاکسی برای ۴۲۷ و ۵۰۱ است. DS4 پنج مجموعه داده مکان تاکسی با شماره های ۳۰۹۰، ۸۲۴۹، ۹۱۷۴، ۹۵۰۰ و ۹۸۳۷ است.

محیط آزمایشی به شرح زیر است: سیستم عامل ویندوز ۱۰ ۶۴ بیتی، پردازنده Inter Core i5-5350U، حافظه ۸G، زبان Visual C #، بر اساس محیط توسعه یکپارچه Microsoft Visual Studio 2015 و پایگاه داده SQL Server 2014.

۵٫۲٫ تجزیه و تحلیل فیلتر Stay Point

به دلیل اشتباهات موقعیت یابی، داده های واقعی نقاط ماندن ممکن است کاملاً بدون تغییر نباشند. ممکن است در یک محدوده عدم دقت موقعیت یابی کوچک تغییر کند. این مقاله آستانه نقطه ماندن را برای کاهش تأثیر خطاهای موقعیت یابی نقطه ماندن بر خوشه بندی در طول حرکت وسیله نقلیه تعریف می کند. موقعیت نقطه ماندن مجاز است در محدوده کوچکی جابجا شود.

به منظور تجزیه و تحلیل تأثیر آستانه ماندن بر مجموعه داده های تجربی این مقاله، تأثیر آستانه ماندن را در پیش پردازش فیلتر نقطه ماندن چهار مجموعه داده با حجم داده های مختلف تجزیه و تحلیل کردیم. با توجه به رویدادهای نقطه اقامت تعریف شده در جدول ۱ ، زمان ماندن آزمایش در این بخش به صورت زیر تنظیم شده است: زمان ماندن DS1 15 دقیقه و زمان باقیمانده مجموعه داده ها ۳۰ دقیقه است.

این آزمایش تعداد نمونه‌های باقی‌مانده را در نقطه‌ای مقایسه می‌کند که آستانه داده‌های اصلی به ترتیب ۰، ۰٫۰۰۰۱، ۰٫۰۰۱ و ۰٫۰۱ است. نتایج در جدول ۳ نشان داده شده است.

هدف از فیلتر کردن نقطه اقامت حذف نقاط ماندن در نظر گرفته شده به عنوان نقاط نویز است. بنابراین، جدول ۳ تعداد نقاط حفظ شده در مجموعه داده های مختلف را هنگام اعمال آستانه های مختلف فهرست می کند. هرچه امتیازهای حفظ شده کمتر باشد، امتیازهای اقامت بیشتر است.

در جدول ۳ نشان داده شده استتعداد زیادی از نقاط داده نمونه گیری مجدد به دلیل ماندن تاکسی در چهار مجموعه داده وجود دارد. هنگامی که آستانه نقطه ماندن ۰ است، برخی از نقاط داده وجود دارند که در چهار مجموعه داده اصلاً حرکت نمی کنند. هنگامی که آستانه نقطه ماندن ۰٫۰۰۰۱، ۰٫۰۰۱ و ۰٫۰۱ باشد، آستانه نقطه ماندن افزایش می یابد و نقاط ماندن بیشتری فیلتر می شوند، بنابراین نقاط نگهداری کاهش می یابد. تفاوت بین آستانه های نقطه ماندن در ۰، ۰٫۰۰۰۱ و ۰٫۰۰۱ معنی دار نیست، اما در ۰٫۰۱، حفظ داده ها به ویژه در DS3 و DS4 بسیار تحت تأثیر قرار می گیرد. در DS3، داده های رزرو شده از ۲۵۷۵ به ۱۴۷۵ کاهش می یابد. در DS4، داده های حفظ شده از ۱۰۱۹۴ به ۳۳۷۷ کاهش می یابد. بنابراین، اگر آستانه بیش از حد بزرگ باشد، مکان رانندگی عادی به عنوان توقف تشخیص داده می شود، نقاط زیادی وجود دارد. حذف شده است، و گرفتن چنین آستانه بزرگی مناسب نیست. از این رو،

طبق طبقه بندی جدول ۱ ، ما پنج رویداد نقطه ماندن انتظار برای چراغ راهنمایی، سوار و پیاده شدن، راه بندان، تعلیق کسب و کار و وقفه های تجاری را در آزمایش در این مقاله تحلیل کردیم و آنها را بر روی چهار مجموعه داده تجزیه و تحلیل کردیم. به ترتیب. هنگامی که طول و عرض جغرافیایی قضاوت می شود، قضاوت می شود که تفاوت بین طول و عرض جغرافیایی ۰ است. نتایج تجربی در جدول ۴ نشان داده شده است.

از جدول ۴ می توان دریافت که در چهار مجموعه مجموعه داده، زمان اقامت تاکسی کمتر از ۳۰ دقیقه اکثریت را به خود اختصاص داده است، که نشان می دهد رویدادهای اقامت عمدتاً ناشی از انتظار برای چراغ های راهنمایی، مسافران و ترافیک است. امتیازهای اقامت کمتری با تعلیق کسب و کار و وقفه های تجاری فیلتر شده است. از جدول ۴ می توان دریافت که تعریف رویدادهای نقطه ماندن در این مقاله صحنه های واقعی را در نظر می گیرد. این روش پیش پردازش برای فیلتر نقطه ماندن واقعی تر و دقیق تر است.

۵٫۳٫ تجزیه و تحلیل نقشه شبکه

ما تأثیر آستانه نقطه ماندن را بر تراکم یک سلول شبکه در مجموعه داده DS3 تجزیه و تحلیل کردیم. ۱۳۷ سلول شبکه تجربی وجود داشت. نتایج تجربی سلول های شبکه ۱-۴۰ در شکل ۵ نشان داده شده است. abscissa شماره سلول شبکه است و مختصات نشان دهنده تعداد نقاط نمونه برداری در هر سلول شبکه پس از نقشه برداری است که مبنای قضاوت در مورد متراکم بودن واحدهای شبکه است.

در شکل ۵ نشان داده شده استکه با افزایش آستانه نقطه ماندن، چگالی هر سلول شبکه زمانی که ۰، ۰٫۰۰۰۱، ۰٫۰۰۱، ۰٫۰۱ باشد روند کاهشی را نشان می دهد. چگالی نسبت معکوس دارد و کاهش چگالی نشان‌دهنده کاهش نقاط نمونه‌گیری داده‌های موجود در طول فرآیند خوشه‌بندی است. هنگامی که آستانه ۰٫۰۱ باشد، چگالی بیشتر سلول های شبکه سریعتر از ۰، ۰٫۰۰۰۱ و ۰٫۰۰۱ کاهش می یابد، و چگالی سلول های شبکه، به عنوان یک شاخص اندازه گیری مهم در خوشه بندی، مستقیماً با متراکم بودن سلول شبکه ارتباط دارد. اگر چگالی خیلی سریع کاهش یابد، سلول‌های شبکه کافی برای برآورده کردن معیارهای قضاوت شبکه‌های متراکم در فرآیند خوشه‌بندی بعدی وجود ندارد، به طوری که شبکه‌های خوشه‌ای در دسترس بسیار کم هستند که بر نتایج خوشه‌بندی تأثیر می‌گذارد. بنابراین، آستانه نقطه ماندن در این مقاله برای گرفتن مقادیر بزرگتر مانند ۰ مناسب نیست.

۵٫۴٫ تجزیه و تحلیل بصری خوشه بندی شبکه متراکم

در این گروه از آزمایش‌ها، آستانه نقطه ماندن روی ۰ تنظیم شد، زمان ماندن ترافیک DS1 Δt روی ۱۵ دقیقه، و DS2، DS3، DS4 زمان ماندن راهبند ترافیک Δt روی ۳۰ دقیقه در قبل تنظیم شد. -مرحله درمان به منظور نشان دادن تأثیر طول های مختلف ضلع شبکه بر روی نتایج خوشه بندی در مرحله نگاشت شبکه، طول ضلع شبکه DS1 و DS4 روی ۰٫۰۱ و طول ضلع شبکه DS2 و DS3 روی ۰٫۰۵ تنظیم شد. آستانه چگالی سلول شبکه روی ۱۰ تنظیم شد. یعنی زمانی که تعداد نقاط نمونه برداری در یک سلول شبکه ۱۰ بود، به عنوان سلول شبکه متراکم تعیین شد.

نتایج تجسم خوشه بندی شبکه متراکم در شکل ۶ نشان داده شده است. شکل ۶ یک نمودار ترکیبی از سلول های شبکه متراکم و توزیع نقطه محل اصلی است. شکل اول خوشه‌های متشکل از سلول‌های شبکه متراکم را در پیش‌زمینه نشان می‌دهد و ثانیاً توزیع نقاط نمونه‌گیری داده‌ها را در قالب رنگ پس‌زمینه نشان می‌دهد. نقاط نمونه برداری داده سلول های شبکه متراکم، نقاط داده در خوشه هستند و نقاط نمونه برداری که در هیچ سلول شبکه ای وجود ندارد، نقاط نویز پراکنده هستند.

نقاط خاکستری روشن در شکل ۶ نقاط نمونه گیری داده ها هستند، یعنی توزیع نقاط موقعیت در مجموعه داده های مختلف پس از فیلتر کردن نقاط ماندگاری. نقاط تیره مانند آبی، قرمز و زرد نشان دهنده نقاط شبکه خوشه ای هستند. از آنجایی که طول جانبی سلول شبکه تجربی داده شده است، سلول شبکه را می توان به طور منحصر به فرد با توجه به هر نقطه پایانی شبکه تعیین کرد. بنابراین، سلول شبکه با نقطه پایانی در سمت چپ پایین سلول شبکه نمایش داده می شود تا نمایش گرافیکی ساده شود.

شکل ۶ نشان می دهد که خوشه بندی پیشنهادی می تواند به طور موثر نقاط نویز پراکنده را تعیین کند. برای مثال، تعداد زیادی نقاط پراکنده در ۱۱۵٫۵-۱۱۶٫۱ درجه عرض شمالی و ۳۹٫۷-۴۰٫۰۵ درجه طول شرقی در نتیجه DS2 شکل ۶ b وجود دارد که در هیچ خوشه ای گنجانده نشده است. علاوه بر این، نتایج تجربی در سایر مجموعه‌های داده نیز نشان می‌دهد که نقاط پراکنده مشابه هیچ تأثیری بر نتایج خوشه‌بندی ندارند، برای مثال، نقاط نمونه‌برداری در اطراف دو خوشه و در محل اتصال در نتایج خوشه‌بندی DS1 در شکل ۶ a.

چهار مجموعه از نتایج تجربی در شکل ۶ a-d نشان می دهد که روش در این مقاله می تواند به طور دقیق خوشه بندی مناطق با تراکم بالا از نقاط نمونه برداری را تعیین کند، که نشان دهنده مناطق با تراکم بالا از توزیع تاکسی است. تاثیر خوبی بر استخراج نقاط حساس شهری دارد.

شکل ۶ همچنین تأثیر طول سلول شبکه را بر روی نگاشت شبکه نشان می دهد. در شکل ۶ a,d سلول های شبکه DS1 و DS4 متراکم تر هستند. در شکل ۶ b,c سلول های شبکه ای DS2 و DS3 نسبتاً پراکنده هستند. این به این دلیل است که طول جانبی شبکه DS1 و DS4 روی ۰٫۰۱ و DS2 و DS3 روی ۰٫۰۵ تنظیم شده است. طول متفاوت شبکه منجر به چگالی و پراکندگی متفاوتی می شود که ناشی از جمع آوری این چهار مجموعه داده از تاکسی های پکن است، بنابراین محدوده مکانی داده ها زیاد نیست.

۵٫۵٫ تجزیه و تحلیل نتایج آزمایش مقایسه ای

در این مقاله، روش خوشه‌بندی مبتنی بر نقطه ماندن و چگالی شبکه (CMSPGD) و DBSCAN مبتنی بر ویژگی ترکیبی (HF_DBSCAN) [ ۳۰ ]، فرآیند انتخاب پارامتر موثر برای DBSCAN (PS_DBSCAN) [ ۳۴ ] مقایسه شد.

(۱): HF_DBSCAN

HF_DBSCAN یک الگوریتم مبتنی بر DBSCAN بهبود یافته است که توسط Luo و همکارانش پیشنهاد شده است. در سال ۲۰۱۷ [ ۳۰ ]. DBSCAN یک الگوریتم کلاسیک مبتنی بر چگالی است که برای یافتن مناطق با چگالی بالا در فضا استفاده می شود و مشتقات مختلفی از الگوریتم برای یافتن مناطق کانونی شهری پیشنهاد شده است. چگالی نقطه فعلی در الگوریتم DBSCAN با فاصله از نقطه فعلی تعیین می شود. تعداد نقاط در یک فاصله معین برای تعادل استفاده می شود. الگوریتم HF_DBSCAN از یک تابع گاوسی به عنوان چگالی نقاط استفاده می کند. روش محاسبه به صورت فرمول (۸) می باشد.

φ (پ من) = \sum j = ۱ n ه - (د من ج σ ۱) ۲

(۸)

جایی که $p_{i} (i = 1, 2, 3 \dots, n)$ نشان دهنده نقطه، $d_{i j}$ نشان دهنده فاصله اقلیدسی بین $p_{i}$ و $p_{j}$ ، و $σ_{1}$ نشان دهنده انحراف معیار است. انحراف معیار در این آزمایش ۰٫۳ است.

(۲): PS_DBSCAN

PS_DBSCAN یک الگوریتم بهبود یافته است که توسط Huang و همکاران ارائه شده است. در ACM Trans در سال ۲۰۱۹ [ ۳۴]. برای الگوریتم اصلی DBSCAN، هیچ تعیین شاخص دقیقی برای انتخاب دو پارامتر طول شعاع و آستانه چگالی وجود ندارد که منجر به خوشه‌بندی نادرست می‌شود. نویسنده روش تعیین این دو مجموعه از پارامترها را با مراحل زیر بهبود بخشید. ابتدا نویسنده طول شعاع بزرگتری را تعیین کرد و سپس به تدریج طول شعاع را کاهش داد. نویسنده تعداد خوشه‌ها را برای مقایسه آستانه چگالی خوشه‌ای با طول شعاع مشاهده کرد. در نتیجه، نویسنده آستانه چگالی را زمانی پیدا کرد که تعداد خوشه‌ها با افزایش آستانه چگالی کاهش یافت و آن را روی آستانه چگالی مناسب زیر طول شعاع گروه قرار داد. آستانه چگالی آخرین مجموعه از تغییرات فوق، مقدار نهایی است. نویسنده مقایسه بین تعداد خوشه ها و طول شعاع را تحت آستانه چگالی مناسب به دست آمده در مرحله قبل مشاهده کرد. طول شعاع مربوط به تعداد بیشتر خوشه ها مقدار مناسب است.

در این مقاله ابتدا DS4 طبق روش انتخاب پارامتر در الگوریتم PS_DBSCAN برای یافتن طول شعاع و آستانه چگالی مناسب مورد آزمایش قرار می‌گیرد. ابتدا طول شعاع بزرگتر ۰٫۰۲۵ را تعیین کردیم و سپس آن را به ترتیب به ۰٫۰۱ و ۰٫۰۰۵ کاهش دادیم. نتایج مقایسه آستانه چگالی و تعداد خوشه ها در این سه گروه از طول شعاع در جدول ۵ ، جدول ۶ و جدول ۷ در زیر نشان داده شده است.

اول از همه، قضاوت می شود که سه گروه وجود دارد که در آن ها آستانه چگالی افزایش می یابد و تعداد خوشه ها در سه مجموعه داده کاهش می یابد: طول شعاع ۰٫۰۰۵ و آستانه چگالی ۶۰، طول شعاع ۰٫۰۱ و آستانه چگالی ۱۱۰، و طول شعاع. ۰٫۰۲۵ و آستانه چگالی ۱۵۰٫ در بین این سه مجموعه داده، آستانه چگالی ۱۵۰ بزرگترین است و مقدار کلیدی برای آخرین تغییر است، بنابراین به عنوان یک پارامتر آستانه چگالی مناسب استفاده می شود. سپس در بین سه گروه داده، داده‌های با آستانه چگالی ۱۵۰ به شرح زیر است: آستانه چگالی با طول شعاع ۰٫۰۲۵ برابر ۱۵۰ و تعداد خوشه‌ها سه است. آستانه چگالی ۱۵۰ با طول شعاع ۰٫۰۰۵ و تعداد خوشه ها سه است. طول شعاع ۰٫۰۲۵ است، آستانه چگالی ۱۵۰ است، و تعداد خوشه ها هفت است. بنابراین، برای DS4، طول شعاع مناسب الگوریتم DBSCAN بر اساس انتخاب پارامتر ۰٫۰۲۵ و آستانه چگالی ۱۵۰ است.

به طور مشابه، طول شعاع مناسب برای DS1، DS2 و DS3 به ترتیب ۰٫۰۰۵، ۰٫۰۲۵، و ۰٫۰۲۵ است و آستانه چگالی به ترتیب ۱۰، ۳۰ و ۵۰ است.

(۳): تجزیه و تحلیل کنتراست دقت خوشه بندی

در این مقاله، نتایج خوشه بندی تجربی HF_DBSCAN و PS_DBSCAN در چهار مجموعه داده در جدول ۸ ، جدول ۹ ، جدول ۱۰ ، جدول ۱۱ ، جدول ۱۲ ، جدول ۱۳ ، جدول ۱۴ ، جدول ۱۵ ، جدول ۱۶ ، نشان داده شده است. ۱۸ و جدول ۱۹ .

ویژگی No در جدول تعداد خوشه را نشان می دهد، m تعداد نقاط داده را در خوشه نشان می دهد. هر چه m بزرگتر باشد ، نقاط بیشتری در خوشه شرکت می کنند و نقاط نویز کمتری دور ریخته می شود. طول و عرض جغرافیایی مختصات مرکز خوشه هستند، یعنی فاصله و حداقل تمام نقاط خوشه تا نقطه. LoadLength نشان دهنده فاصله خوشه بندی خوشه، مجموع فواصل از همه نقاط تا مرکز خوشه است. محاسبه به صورت فرمول (۹) است.

L o a d L e n g t h = \sum p \in c l u s t e r د i s (p, c e n t e r)

(۹)

جایی که p نشان دهنده عنصر خوشه در خوشه است. مرکز نشان دهنده مرکز خوشه بندی خوشه، یعنی مختصات طول و عرض جغرافیایی است. میانگین نشان دهنده میانگین فاصله تجمع هر نقطه است که در فرمول (۱۰) محاسبه شده است.

A v g = L o a d L e n g تی ساعت متر

(۱۰)

میانگین چگالی متوسط نقاط در خوشه را نشان می دهد. هر چه میانگین بزرگتر باشد ، نقاط در خوشه چگال تر می شوند. اگر نقاط بیشتر در خوشه و متراکم تر باشد، اثر خوشه بندی هر خوشه بهتر است.

جدول ۸ ، جدول ۹ و جدول ۱۰ نشان می دهد که الگوریتم پیشنهادی و الگوریتم PS_DBSCAN مقادیر m کمتری نسبت به الگوریتم HF_DBSCAN برای مجموعه داده DS1 دارند، که نشان می دهد در مجموعه داده های مقیاس کوچک، الگوریتم و الگوریتم PS_DBSCAN نقاط از دست رفته بیشتری دارند. . ثانیاً، مقادیر LoadLength و میانگین در جدول گروه نشان می دهد که فاصله درون خوشه ایجاد شده توسط الگوریتم HF_DBSCAN زیاد است، که نشان می دهد کیفیت دقت خوشه بندی به خوبی الگوریتم این مقاله و الگوریتم PS_DBSCAN نیست.

جدول ۱۱ ، جدول ۱۲ ، جدول ۱۳ ، جدول ۱۴ ، جدول ۱۵ ، جدول ۱۶ ، جدول ۱۷ ، جدول ۱۸ و جدول ۱۹ نشان می دهد که مقادیر m سه الگوریتم در مجموعه داده های DS2، DS3 و DS4 تفاوت چندانی با هم ندارند. نشان می دهد که سه مجموعه الگوریتم اساساً در تعداد نقاط نمونه گیری از نتایج خوشه بندی یکسان هستند. الگوریتم مقایسه بالاتر است که نشان می دهد دقت خوشه بندی الگوریتم در این مقاله در فاصله درون خوشه ای بدتر است. این به این دلیل است که فرآیند نگاشت شبکه ای از خوشه بندی در این مقاله کاهش دقت خاصی را به همراه خواهد داشت.

جدول ۸ ، جدول ۹ ، جدول ۱۰ ، جدول ۱۱ ، جدول ۱۲ ، جدول ۱۳ ، جدول ۱۴ ، جدول ۱۵ ، جدول ۱۶ ، جدول ۱۷ ، جدول ۱۸ و جدول ۱۹ نشان می دهد که اگرچه الگوریتم cluster HF_DBSCAN بسیاری از clusters را تولید می کند. نقاط پراکنده و عناصر کمتر. الگوریتم خوشه بندی و الگوریتم PS_DBSCAN در این مقاله منجر به داده های یکنواخت تر می شود. به عنوان مثال، جدول ۱۴ ، جدول ۱۵ و جدول ۱۶نشان می دهد که روش خوشه بندی در این مقاله و الگوریتم PS_DBSCAN دو تا سه خوشه و الگوریتم HF_DBSCAN نه خوشه تولید می کند، اما با توجه به مقدار m.، خوشه های ۲، ۳، ۴، ۵، ۶، ۷ و ۹ فقط یک نقطه داده دارند. این نوع داده های آزمایشی را می توان به عنوان نویز حذف کرد یا در خوشه های دیگر ادغام کرد. نتایج مشابهی برای سایر مجموعه داده ها به دست آمده است. خوشه های تشکیل شده توسط الگوریتم خوشه بندی در این مقاله و الگوریتم PS_DBSCAN معقول تر، متعادل تر و پایدارتر هستند. با این حال، در الگوریتم PS_DBSCAN، پارامترها بهینه‌سازی می‌شوند تا نتایج خوشه‌بندی یکنواخت‌تر شود و اجرای الگوریتم نسبتاً پیچیده است. بنابراین، الگوریتم این مقاله ساده تر و کارآمدتر از الگوریتم PS_DBSCAN برای تشکیل خوشه های منطقی است.

به طور خلاصه، در مقایسه با الگوریتم PS_DBSCAN از نظر اثر خوشه‌بندی، الگوریتم در این مقاله ساده‌تر است و نقاط نویز کمتری را حذف می‌کند. در مقایسه با الگوریتم HF_DBSCAN، خوشه های تشکیل شده توسط این روش یکنواخت تر و معقول تر هستند.

(۴): تحلیل مقایسه ای زمان اجرا

این آزمایش همچنین زمان اجرای الگوریتم در این مقاله را با الگوریتم‌های HF_DBSCA N و PS_DBSCAN مقایسه و تحلیل می‌کند. نتایج تجربی برای چهار مجموعه داده در جدول ۲۰ نشان داده شده است.

جدول ۲۰نشان می‌دهد که مصرف زمان اجرای الگوریتم خوشه‌بندی در این مقاله هنگام پردازش مجموعه داده‌های هم اندازه بسیار کمتر از الگوریتم مقایسه است. با ادامه افزایش تعداد مجموعه‌های شی داده، زمان اجرای الگوریتم مقایسه به شدت افزایش می‌یابد. در این مقاله، افزایش زمان اجرای الگوریتم خوشه‌بندی مبتنی بر شبکه و چگالی بر اساس سلول‌های شبکه بسیار کمتر از الگوریتم مقایسه است. در هنگام برخورد با مجموعه داده های بزرگ، نسبت به الگوریتم های مقایسه مزایایی دارد. این به این دلیل است که الگوریتم از یک الگوریتم خوشه بندی شبکه برای تقسیم شبکه استفاده می کند، به طوری که شی پردازش شده یک نقطه داده نیست، بلکه یک سلول شبکه تقسیم شده است، و الگوریتم خوشه بندی DBSCAN بهبود یافته روی اشیاء داده عمل می کند.

در این آزمایش، خوشه بندی برای سلول های شبکه ای انجام می شود. تعداد سلول های شبکه پس از تقسیم فضا و تعداد سلول های غیر متراکم نیز بر کارایی این آزمایش تأثیر می گذارد و قضاوت های بیشتری در مورد سلول های شبکه غیر متراکم نیز لازم است. اما کارایی کلی هنوز به طور قابل توجهی بهتر از الگوریتم مقایسه است.

۶٫ نتیجه گیری

در این مقاله، یک روش خوشه بندی بر اساس نقاط ماندن و چگالی شبکه پیشنهاد شده است. ابتدا، الگوریتم فیلتر نقطه اقامت برای جلوگیری از تأثیر رویدادهای توقف تاکسی بر تراکم سلول‌های شبکه استفاده می‌شود. در مرحله دوم، نقشه‌برداری شبکه و قضاوت نقطه مرزی خوشه برای جلوگیری از تأثیر نقاط نویز پراکنده بر مجموعه نمونه‌برداری در حین انجام استخراج خوشه‌ای استفاده می‌شود. در نهایت، از روش خوشه‌بندی شبکه‌ای برای بهبود قابل‌توجه بازده زمانی روش‌های موجود استفاده می‌شود. با این حال، طبقه بندی نقاط اقامت عمدتا از منظر زمان اقامت است. دانه بندی بیشتر اصلاح نشده است، که ممکن است باعث قضاوت نادرست برخی از رویدادهای اقامت شود. در کار آینده، مبنای معنایی واقع گرایانه برای قضاوت در مورد نقطه اقامت تقویت خواهد شد و مقوله نقطه ماندن اصلاح خواهد شد. تحقیق در مورد فیلتر نقطه ماندن را عمیق تر می کند. علاوه بر این، معیارهای قضاوت در مورد اینکه آیا دو شبکه سلولی در یک خوشه هستند یا خیر، عمدتاً با توجه به تعداد نقاط نمونه‌برداری به اندازه کافی جامع نیستند. در فرآیند خوشه بندی، یک معیار قضاوت بیشتر این است که آیا توزیع نقطه نمونه برداری در دو واحد شبکه متمرکز است یا خیر، که می تواند منجر به خوشه بندی شبکه دقیق تری شود.

منابع

شولز، RW; Lu, Y. تشخیص الگوهای فعالیت پویا در سطح جمعی از داده‌های مسیر با حجم زیاد. بین المللی جی. جئوگر. Inf. علمی ۲۰۱۴ ، ۲۸ ، ۹۴۶-۹۶۳٫ [ Google Scholar ] [ CrossRef ]
شان، جی. آلوز، آ. رودریگز، اف. فریرا، جی.، جونیور. Pereira، FC داده های نقطه مورد علاقه استخراج از شبکه های اجتماعی برای طبقه بندی و تفکیک کاربری زمین شهری. محاسبه کنید. محیط زیست سیستم شهری ۲۰۱۵ ، ۵۳ ، ۳۶-۴۶٫ [ Google Scholar ]
یو، ی. ژوانگ، ی. بله، پیش از این؛ زی، جی. Ma، CL; لی، QQ اندازه گیری استفاده مختلط مبتنی بر POI و روابط آنها با سرزندگی محله. بین المللی جی. جئوگر. Inf. سیستم ۲۰۱۷ ، ۳۱ ، ۶۵۸-۶۷۵٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مینگ، ن. او، س. جینگ، جی. پیش‌بینی جریان مسافر در مترو تحت رویدادها با رسانه‌های اجتماعی. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۷ ، ۱۸ ، ۱۶۲۳-۱۶۳۲٫ [ Google Scholar ]
یانگ، ایکس. چن، آ. نینگ، بی. تانگ، تی. اندازه گیری تنوع مسیر برای شبکه های حمل و نقل ریلی شهری: مطالعه موردی شبکه متروی پکن. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۷ ، ۱۸ ، ۲۵۹-۲۶۸٫ [ Google Scholar ] [ CrossRef ]
ژانگ، اف. ژائو، جی. تیان، سی. خو، سی. لیو، ایکس. Rao, L. تقسیم بندی مکانی-زمانی سفرهای مترو با استفاده از داده های کارت هوشمند. IEEE Trans. وه تکنولوژی ۲۰۱۶ ، ۶۵ ، ۱۱۳۷-۱۱۴۹٫ [ Google Scholar ] [ CrossRef ]
Le، MK; باسکار، ا. Chung, E. تقسیم بندی مسافران با استفاده از داده های کارت هوشمند. IEEE Trans. هوشمند ترانسپ سیستم ۲۰۱۵ ، ۱۶ ، ۱۵۳۷-۱۵۴۸٫ [ Google Scholar ]
ایتو، م. یوکویاما، دی. تویودا، م. تومیتا، ی. کاوامورا، اس. Kitsuregawa، M. کاوش بصری تغییرات در جریان مسافران و توییت‌ها در شبکه مترو Mega-City. IEEE Trans. کلان داده ۲۰۱۶ ، ۲ ، ۸۵-۹۹٫ [ Google Scholar ] [ CrossRef ]
چن، ی. Chao، S. تجزیه و تحلیل عملکرد رفتار حسگر گوشی هوشمند برای تشخیص فعالیت انسانی. IEEE Access ۲۰۱۷ ، ۵ ، ۳۰۹۵–۳۱۱۰٫ [ Google Scholar ] [ CrossRef ]
ژانگ، دبلیو. چی، جی. باند، پ. هوآ، ال. لی، اس. Wu, Z. تشخیص و ارزیابی رویداد اجتماعی در مقیاس شهر با ردیابی تاکسی. Acm Trans. هوشمند سیستم تکنولوژی ۲۰۱۵ ، ۶ ، ۱-۲۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
فوکس، جی. استنج، اچ. هکر، دی. آندرینکو، ن. آندرینکو، جی. ساخت تفسیر معنایی رفتارهای حرکتی روتین و غیرعادی از داده های بزرگ. Sigspatial Spec. ۲۰۱۵ ، ۷ ، ۲۷-۳۴٫ [ Google Scholar ] [ CrossRef ]
Unsalan, C. اندازه گیری توسعه زمین در مناطق شهری با استفاده از نمودار ویژگی های نظری و آماری شرطی. IEEE Trans. Geosci. Remote Sens. ۲۰۰۷ , ۴۵ , ۳۹۸۹–۳۹۹۹٫ [ Google Scholar ] [ CrossRef ]
یین، جی. سلیمان، ع. یین، دی. وانگ، اس. ترسیم مرزهای شهری از یک شبکه تحرک تعاملات فضایی: مطالعه موردی بریتانیای کبیر با داده های توئیتر موقعیت جغرافیایی. بین المللی جی. جئوگر. Inf. سیستم ۲۰۱۷ ، ۳۱ ، ۱۲۹۳-۱۳۱۳٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
یوان، نیوجرسی؛ ژنگ، ی. Xie، X. وانگ، ی. Xiong، H. کشف مناطق عملکردی شهری با استفاده از مسیرهای فعالیت پنهان. IEEE Trans. بدانید. مهندسی داده ۲۰۱۵ ، ۲۷ ، ۷۱۲-۷۲۵٫ [ Google Scholar ] [ CrossRef ]
سرکار، س. چاولا، س. Parambath، SP; سریواستاوا، جی. Borge-Holthoefer، J. استنتاج ساختار شهری موثر از دینامیک جریان ترافیک. IEEE Trans. کلان داده ۲۰۱۷ ، ۳ ، ۱۸۱-۱۹۳٫ [ Google Scholar ] [ CrossRef ]
کنگ، ایکس. فنگ، ایکس. وانگ، جی. رحیم، ع. Das، SK پیشنهاد سرویس ترکیبی زمان-مکان-رابطه بر اساس داده های مسیر تاکسی. IEEE Trans. Ind. اطلاع رسانی. ۲۰۱۷ ، ۱۳ ، ۱۲۰۲-۱۲۱۲٫ [ Google Scholar ] [ CrossRef ]
لی، جی. شین، آی. پارک، جی.-ال. تجزیه و تحلیل الگوی تحویل مسافر برای توصیه مکان تاکسی. در مجموعه مقالات چهارمین کنفرانس بین المللی محاسبات شبکه ای و مدیریت اطلاعات پیشرفته، Gyeongju، کره، ۲-۴ سپتامبر ۲۰۰۸٫ جلد ۱، ص ۱۹۹–۲۰۴٫ [ Google Scholar ]
Thuillier، E. معلیک، ال. لامروس، س. Caminada، A. خوشه بندی الگوهای هفتگی تحرک انسان از طریق داده های تلفن همراه. IEEE Trans. اوباش محاسبه کنید. ۲۰۱۸ ، ۱۷ ، ۸۱۷-۸۳۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
جین، AK; قانون، خوشه‌بندی داده‌های MHC: معضل کاربر. در کنفرانس بین المللی تشخیص الگو و هوش ماشینی ؛ PReMI 2005. نکات سخنرانی در علوم کامپیوتر. Springer: برلین/هایدلبرگ، آلمان، ۲۰۰۵; جلد ۳۷۷۶، ص ۱-۱۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شی، ایکس. گوا، ز. زینگ، اف. کای، جی. یانگ، ال. خودآموزی برای خوشه بندی چهره. تشخیص الگو ۲۰۱۸ ، ۷۹ ، ۲۷۹-۲۸۹٫ [ Google Scholar ] [ CrossRef ]
دیگو، IMd; Siordia، OS؛ فرناندز-ایزابل، آ. کوند، سی. Cabello، E. ترتیب داده های ذهنی با استفاده از تکنیک های خوشه بندی برای آموزش سیستم های خبره. سیستم خبره Appl. ۲۰۱۹ ، ۱۱۵ ، ۱-۱۵٫ [ Google Scholar ] [ CrossRef ]
موسویراد، س.ج. ابراهیم پور کومله، ح. Schaefer, G. خوشه بندی تصویر موثر بر اساس جستجوی ذهنی انسان. Appl. محاسبات نرم. ۲۰۱۹ ، ۷۸ ، ۲۰۹–۲۲۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هو، جی. گائو، اچ. Li, X. DSets-DBSCAN: الگوریتم خوشه بندی بدون پارامتر. IEEE Trans. فرآیند تصویر ۲۰۱۶ ، ۲۵ ، ۳۲-۳۹٫ [ Google Scholar ] [ CrossRef ] [ PubMed ]
غفاری، ر. گلپرداز، م. هلفروش، ام اس; Danyali, H. یک الگوریتم سریع و وزنی CRF بر اساس یک تولید سوپرپیکسل دو مرحله ای برای تقسیم بندی تصویر SAR. بین المللی J. Remote Sens. ۲۰۲۰ , ۴۱ , ۳۵۳۵–۳۵۵۷٫ [ Google Scholar ] [ CrossRef ]
ژو، تی. لیو، ایکس. کیان، ز. چن، اچ. تائو، F. به روز رسانی دینامیک و نظارت بر ورود AOI از طریق خوشه بندی مکانی-زمانی نقاط رها. پایداری ۲۰۱۹ ، ۱۱ ، ۶۸۷۰٫ [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
فری، بی جی؛ Dueck، D. خوشه بندی با ارسال پیام بین نقاط داده. Science ۲۰۰۷ ، ۳۱۵ ، ۹۷۲-۹۷۶٫ [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
شویر، جی. بوروسو، جی. الگوریتم‌های خوشه‌بندی حرکات فردی و داده‌کاوی جغرافیایی برای برجسته کردن نقاط داغ در مسیرهای ناوبری شخصی. در مجموعه مقالات کنفرانس بین المللی علوم محاسباتی ۲۰۱۱، سانتاندر، اسپانیا، ۲۰ تا ۲۳ ژوئن ۲۰۱۱٫ ص ۴۵۴-۴۶۵٫ [ Google Scholar ]
ژو، سی. دان، اف. لودفورد، پی. شکر، س. تروین، ال. کشف مکان‌های معنادار شخصی: یک رویکرد خوشه‌بندی تعاملی. ACM Trans. Inf. سیستم ۲۰۰۷ ، ۲۵ ، ۱۲-۱۷٫ [ Google Scholar ] [ CrossRef ]
هوانگ، اس. ایوانز، سی. هانکه، تی. تشخیص توقف قسمت از مسیرهای GPS با شکاف. در دیدن شهرها از طریق داده های بزرگ ؛ Springer: Cham, Switzerland, 2017; ص ۴۲۷-۴۳۹٫ [ Google Scholar ]
لو، تی. ژنگ، ایکس. خو، جی. فو، ک. Ren, W. الگوریتم DBSCAN بهبود یافته برای تشخیص توقف در مسیرهای فردی. ISPRS Int. J. Geo-Inf. ۲۰۱۷ ، ۶ ، ۶۳-۷۴٫ [ Google Scholar ] [ CrossRef ]
ژائو، کیو. شی، ی. لیو، کیو. فرانتی، پی. الگوریتم خوشه‌بندی در حال رشد شبکه برای داده‌های جغرافیایی-مکانی. تشخیص الگو Lett. ۲۰۱۵ ، ۵۳ ، ۷۷-۸۴٫ [ Google Scholar ] [ CrossRef ]
یوان، جی. ژنگ، ی. Xie، X. Sun, G. رانندگی با دانش از دنیای فیزیکی. در مجموعه مقالات هفدهمین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، سن دیگو، کالیفرنیا، ایالات متحده آمریکا، ۲۱ تا ۲۴ اوت ۲۰۱۱٫ صص ۳۱۶-۳۲۴٫ [ Google Scholar ]
یوان، جی. ژنگ، ی. ژانگ، سی. زی، دبلیو. Xie، X. سان، جی. Huang, Y. T-drive: مسیرهای رانندگی بر اساس مسیرهای تاکسی. در مجموعه مقالات هجدهمین کنفرانس بین المللی SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، ۲ تا ۵ نوامبر ۲۰۱۰٫ صص ۹۹-۱۰۸٫ [ Google Scholar ]
هوانگ، ی. شیائو، ز. یو، ایکس. وانگ، دی. هاویاریمانا، وی. بای، جی. ساخت شبکه جاده با تقاطع های پیچیده بر اساس داده های مسیر خودروهای خصوصی نمونه برداری پراکنده. ACM Trans. بدانید. کشف کنید. داده ۲۰۱۹ ، ۱۳ ، ۳۵٫ [ Google Scholar ] [ CrossRef ]

شکل ۱٫ نقطه مرکز داده و نقطه مرکز شبکه.

شکل ۲٫ فرآیند ترجمه مرکز شبکه (p → p′).

شکل ۳٫ قضاوت نقاط مرزی خوشه.

شکل ۴٫ خوشه بندی سلول های شبکه متراکم.

شکل ۵٫ تأثیر آستانه نقطه ماندن بر تراکم سلول شبکه. نتایج ( الف ) سلول های شبکه شماره ۱-۱۰ ( ب ) شماره سلول های شبکه ۱۱-۲۰ ( ج ) شماره سلول های شبکه ۲۱-۳۰ ( d ) شماره سلول های شبکه ۲۱-۳۰٫

شکل ۶٫ تجسم نتایج خوشه بندی در مجموعه داده های مختلف. نتایج خوشه بندی روی ( a ) DS1 ( b ) DS2 ( c ) DS3 ( d ) DS4.

هوش مکانی اتیم تحقیقاتی ونوس نصیرفام

روش‌های خوشه‌بندی بر اساس نقاط ماندن و تراکم شبکه برای تشخیص نقطه اتصال