حلقه تودرتو کلاستر k -الگوریتم پیوستن دورترین همسایه برای شبکه های فضایی

این مقاله پرس و جوهای پیوستن k- دورترین همسایه ( k FN) را در شبکه های فضایی در نظر می گیرد که فاصله بین دو نقطه طول کوتاه ترین مسیری است که آنها را به هم متصل می کند. با در نظر گرفتن یک عدد صحیح مثبت k ، مجموعه ای از نقاط پرس و جو Q ، و مجموعه ای از نقاط داده P ، پرس و جو پیوستن k FN دورترین نقاط داده را از هر نقطه پرس و جو در Q بازیابی می کند . بسیاری از برنامه های کاربردی واقعی با استفاده از k وجود داردجستارهای FN، از جمله هوش مصنوعی، هندسه محاسباتی، بازیابی اطلاعات و تشخیص الگو. با این حال، راه حل های مبتنی بر فاصله اقلیدسی یا جستجوی نزدیکترین همسایه به دلیل تفاوت در تعریف مسئله برای هدف ما مناسب نیستند. بنابراین، این مقاله یک الگوریتم اتصال حلقه تو در تو (CNLJ) را پیشنهاد می‌کند، که نقاط پرس و جو (نقاط داده) را به خوشه‌های پرس و جو (خوشه‌های داده) خوشه‌بندی می‌کند و تعداد k پرس‌وجوهای مورد نیاز برای اجرای k FN را کاهش می‌دهد. یک مطالعه تجربی با استفاده از نقشه‌های راه واقعی برای تأیید برتری و مقیاس‌پذیری الگوریتم CNLJ در مقایسه با راه‌حل‌های مرسوم در شرایط مختلف انجام شد.

کلید واژه ها:

پیوستن حلقه تو در تو کلاستر ; k -دورترین همسایه join ; شبکه فضایی ; اجرای مشترک

۱٫ مقدمه

در این مطالعه، ما پردازش کارآمد k -دورترین همسایه ( k FN) را در شبکه‌های فضایی بررسی می‌کنیم که در آن فاصله بین دو نقطه با طول کوتاه‌ترین مسیری که آنها را به هم متصل می‌کند، تعریف می‌شود. پیوستن k FN هر نقطه پرس و جو q در Q را با k نقاط داده در P که دورترین نقطه از پرس و جو q هستند را با یک عدد صحیح مثبت k ، مجموعه ای از نقاط پرس و جو Q و مجموعه ای از نقاط داده P ترکیب می کند. k _پرس و جو پیوستن FN کاربردهای واقعی در سیستم های توصیه گر دارد، جایی که دورترین همسایگان می توانند تنوع توصیه ها را افزایش دهند [ ۱ ، ۲ ]. جستجوی دورترین همسایه نیز عنصری در برنامه های خوشه بندی [ ۳ ]، خوشه بندی کامل پیوند [ ۴ ] و الگوریتم های کاهش ابعاد غیرخطی [ ۵ ] است. بنابراین، توانایی پردازش سریع k جستارهای پیوستن FN یک نگرانی عملی مهم برای بسیاری از برنامه ها است [ ۶ ، ۷ ، ۸ ، ۹ ، ۱۰ ، ۱۱ ، ۱۲ ، ۱۳ ، ۱۴ ].

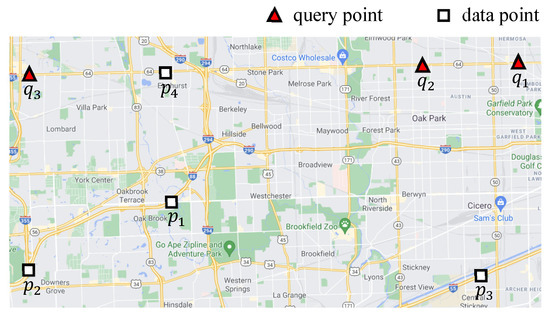
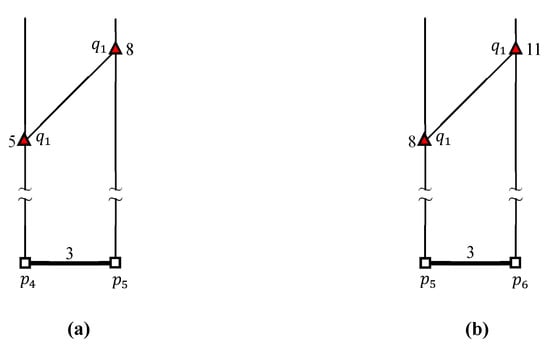
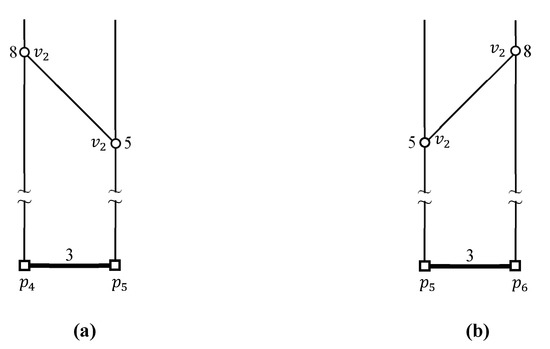
شکل ۱ نمونه ای از اتصال k FN را بین مجموعه Q از نقاط پرس و جو و مجموعه P از نقاط داده در یک شبکه فضایی نشان می دهد، که در آن فرض می شود ، ، و داده می شود. در این مقاله، اتصال k FN به صورت مشخص شده است . در این مثال، داده‌ها به دورترین فاصله از آن اشاره می‌کنند ، ، و هستند ، ، و ، به ترتیب، که می تواند توسط . برعکس، پرس و جو در دورترین نقطه قرار دارد ، ، ، و هستند ، ، ، و ، به ترتیب، که می تواند توسط . این به سادگی ثابت می کند که k اتصالات FN جابجایی نیستند، به عنوان مثال، . توجه داشته باشید که این مطالعه در نظر دارد . مشکل مکان تأسیسات، که مکان رقابتی یک تأسیسات جدید را تعیین می کند، مانند زباله سوزها، کوره های آدم سوزی، کارخانه های شیمیایی، سوپرمارکت ها، و ایستگاه های پلیس، در زندگی واقعی هنگام استفاده از برنامه های کاربردی جست و جوی k FN بسیار مهم است. به ویژه، تعیین مکان بهینه تسهیلات هنوز یک مشکل باز است [ ۱۵ ، ۱۶ ]. در مواجهه با چنین مشکل تحقیقاتی، ارزیابی کارآمد پرس و جو پیوستن k FN بسیار مفید است. فرض کنید که نقاط پرس و جو از طریق نشان دهنده امکانات ناخوشایند مانند زباله سوز و کارخانه های شیمیایی است، در حالی که داده ها از طریق نشان دهنده آپارتمان های اجاره ای موجود است. این مثال ممکن است یک اتصال FN بین مجموعه‌ای از امکانات ناخوشایند Q و مجموعه‌ای از آپارتمان‌های اجاره‌ای موجود P را در نظر بگیرد، که می‌تواند «جفت‌های سفارش‌داده‌شده یک تسهیلات ناخوشایند q و آپارتمان اجاره‌ای موجود p را پیدا کند، به‌گونه‌ای که آپارتمان اجاره‌ای p دورتر از امکانات ناخوشایند q نسبت به سایر آپارتمان های اجاره ای موجود است. طبیعتا، یا ممکن است آپارتمان رقابتی از نظر فاصله تا امکانات ناخوشایند باشد.

پرس و جو پیوستن k FN باید فواصل بین هر جفت داده و نقاط پرس و جو را به طور مکرر محاسبه کند، که منجر به زمان پردازش پرس و جو طولانی می شود. یک راه حل ساده برای پیوستن پرس و جو k FN بین مجموعه پرس و جو Q و مجموعه داده P به طور مکرر تمام نقاط داده در P را برای هر نقطه پرس و جو در Q اسکن می کند تا فاصله بین هر جفت پرس و جو و نقاط داده را محاسبه کند. . این راه حل ساده در اکثر موارد غیرقابل قبول است زیرا به طور مکرر نقاط داده کاندید را برای هر نقطه پرس و جو بازیابی می کند. با این حال، ممکن است در مواردی که نقاط پرس و جو به طور یکنواخت در سراسر منطقه توزیع شده اند در نظر گرفته شود. با این حال، جستارهای پیوستن k FN، علیرغم اهمیت آنها، توجه کافی را برای شبکه های فضایی دریافت نکرده اند. این مقاله یک الگوریتم اتصال حلقه تو در تو (CNLJ) خوشه ای را برای شبکه های فضایی برای حل مشکل پردازش کارآمد k پیشنهاد می کند.جستارهای پیوستن FN به طور خاص، با استفاده از اتصال شبکه فضایی، نقاط پرس و جو (نقاط داده) به خوشه های پرس و جو (خوشه های داده) خوشه بندی می شوند. الگوریتم CNLJ از یک محاسبات مشترک برای خوشه های پرس و جو استفاده می کند تا از محاسبات غیر ضروری فاصله بین داده ها و نقاط پرس و جو جلوگیری کند. الگوریتم CNLJ چندین مزیت نسبت به راه حل سنتی دارد: (۱) با استفاده از اتصال شبکه فضایی برای محاسبات مشترک، نقاط پرس و جو (نقاط داده) را خوشه بندی می کند، (۲) به سرعت نقاط داده کاندید را به یکباره برای نقاط پرس و جو خوشه ای بازیابی می کند، و ( ۳) نقاط داده کاندید را برای هر نقطه پرس و جو به طور جداگانه بازیابی نمی کند. تا جایی که ما می دانیم، این اولین تلاش برای مطالعه جستارهای پیوستن k FN برای شبکه های فضایی است.

مشارکت های اولیه این مطالعه به شرح زیر است:

این مقاله یک الگوریتم اتصال حلقه تو در تو را برای ارزیابی سریع شبکه فضایی k پرس‌وجوهای پیوستن FN ارائه می‌کند. الگوریتم CNLJ نقاط پرس و جو را قبل از بازیابی نقاط داده کاندید برای نقاط پرس و جو خوشه ای به یکباره خوشه بندی می کند. در نتیجه، نقاط داده کاندید را برای هر نقطه پرس و جو چندین بار بازیابی نمی کند.
درستی الگوریتم CNLJ از طریق استدلال ریاضی نشان داده می شود. علاوه بر این، یک تحلیل نظری برای روشن شدن مزایا و معایب الگوریتم CNLJ در مورد فشردگی مکانی نقطه پرس و جو ارائه شده است.
یک مطالعه تجربی با تنظیمات مختلف برای نشان دادن برتری و مقیاس پذیری الگوریتم CNLJ انجام شد. با توجه به نتایج، الگوریتم CNLJ تا ۵۰٫۸ برابر از الگوریتم های اتصال معمولی بهتر عمل می کند.

بقیه این مقاله به شرح زیر سازماندهی شده است: بخش ۲ تحقیقات مرتبط را مرور می کند و برخی از دانش پیش زمینه را ارائه می دهد. بخش ۳ خوشه بندی نقاط پرس و جو (نقاط داده) و محاسبه حداکثر و حداقل فاصله بین یک نقطه مرزی و یک خوشه داده را توصیف می کند. بخش ۴ الگوریتم CNLJ را برای ارزیابی سریع جستارهای پیوستن k FN در شبکه های فضایی ارائه می کند. بخش ۵ نتایج آزمایش‌ها را با استفاده از CNLJ و الگوریتم‌های اتصال مرسوم با تنظیمات مختلف ارائه می‌کند. در نهایت، نتایج این مطالعه در بخش ۶ مورد بحث قرار گرفته است.

۲٫ پس زمینه

بخش ۲٫۱ کارهای مرتبط را ارائه می دهد و بخش ۲٫۲ اصطلاحات و نشانه های مورد استفاده در این مطالعه را تعریف می کند.

۲٫۱٫ کار مرتبط

بسیاری از مطالعات پرس و جوهای فضایی را بر اساس جستجوی دورترین همسایه (FN) در نظر گرفته اند [ ۶ ، ۷ ، ۸ ، ۹ ، ۱۰ ، ۱۱ ، ۱۳ ، ۱۴ ، ۱۷ ، ۱۸ ، ۱۹ ، ۲۰ ]. کورن و موتوکریشنان [ ۲۱ ] برای به دست آوردن مجموعه تأثیر ضعیف، مفهوم پرسش دورترین همسایه معکوس (RFN) را پیشگام کردند. با توجه به مجموعه ای از نقاط داده P و یک نقطه پرس و جو q ، پرس و جو RFN مجموعه ای از نقاط داده را بازیابی می کند. به طوری که q دورترین همسایه آنها در بین تمام نقاط است . این پرس و جو RFN تک رنگ (MRFN) است [ ۸ ، ۹ ، ۱۳ ، ۱۴ ، ۱۹ ]. نسخه دیگری از پرس و جو RFN، پرس و جو دورترین همسایه معکوس دو رنگی (BRFN) است [ ۱۰ ، ۱۳ ، ۱۴ ، ۲۲ ]. با توجه به مجموعه ای از نقاط داده P ، مجموعه ای از نقاط پرس و جو Q ، و یک نقطه پرس و جو q در Q ، پرس و جو BRFN مجموعه ای از نقاط داده p را در P بازیابی می کند به طوری که q دورترین همسایه p در بین تمام نقاط پرس و جو در Q باشد.. مطالعات زیادی برای پردازش پرس و جوهای RFN برای فضای اقلیدسی [ ۸ ، ۹ ، ۱۴ ، ۱۹ ، ۲۲ ] و برای شبکه های فضایی [ ۱۰ ، ۱۳ ] انجام شده است. یائو و همکاران [ ۱۴ ] الگوریتم‌های دورترین سلول مترقی و دورترین سلول بدنه محدب را برای پاسخ به پرسش‌های RFN با استفاده از درخت R پیشنهاد کرد [ ۲۳ ، ۲۴ ]. راه حلی برای پاسخ به پرس و جوهای k FN معکوس در فضای اقلیدسی برای مقادیر دلخواه k [ ۲۲ ] ارائه شد. لیو و همکاران [ ۱۹ ] مفهوم گروه R k را پیشنهاد کردFN پرس و جو در فضای مانع و ارائه یک الگوریتم بهینه سازی پرس و جو بر اساس نمودار Voronoi. تران و همکاران [ ۱۰ ] راه حلی برای پرس و جوهای RFN و پرس و جوهای Rk FN در شبکه های جاده ای با استفاده از ویژگی های مرتبط با نمودار Voronoi و الگوریتم Dijkstra پیشنهاد کرد. خو و همکاران [ ۱۳ ] الگوریتم های کارآمدی را بر اساس نشانه ها و پارتیشن بندی سلسله مراتبی برای پردازش پرس و جوهای RFN تک رنگ و دو رنگ در شبکه های فضایی ارائه کرد. نسخه تقریبی مسئله، که به عنوان جست و جوی دورترین همسایه ( c -AFN ) شناخته می شود ، به دلیل دشواری در طراحی یک روش کارآمد برای جستجوی دقیق FN در فضای با ابعاد بالا، به طور فعال مورد مطالعه قرار گرفته است [ ۶ ، ۱۷ ،۱۸ ، ۲۵ ]. هوانگ و همکاران [ ۱۸ و ۲۵ ] مفهوم جدیدی از خانواده هشینگ حساس به محل معکوس (LSH) را معرفی کرد و توابع LSH آگاه از پرس و جو معکوس را توسعه داد. آنها دو طرح هش را برای جستجوی c – AFN با ابعاد بالا در حافظه خارجی پیشنهاد کردند. لیو و همکاران [ ۱۷ ] یک الگوریتم تقریبی با تضمین نظری برای جست‌وجوی c -AFN با ابعاد بالا در حافظه خارجی ایجاد کرد. کرتین و همکاران [ ۶ ] الگوریتمی با تضمین تقریب مطلق برای جستجوی FN در فضای با ابعاد بالا پیشنهاد کرد. برای تخمین دشواری مشکل جستجوی FN، یک معیار نظری اطلاعاتی از سختی ارائه شد [ ۶ ]]. پرس و جوهای دورترین مکان غالب (FDL) در [ ۲۶ ] پیشنهاد شد. یک پرس و جو FDL مکان را بازیابی می کند به طوری که فاصله تا نزدیک‌ترین شی غالب آن در P با توجه به مجموعه‌ای از نقاط داده P با ویژگی‌های فضایی و غیر مکانی، مجموعه‌ای L از مکان‌های کاندید، و بردار شایستگی طراحی به حداکثر می‌رسد. برای L. _ گائو و همکاران [ ۷ ] پرس و جوهای کل دورترین همسایه k (AkFN ) را که با توابع تجمع، مانند min، max، و sum تعریف می شوند، مورد مطالعه قرار دادند و الگوریتم های MB و BF را بر اساس درخت R ارائه کردند [ ۲۳ ، ۲۴ ] . یک پرس و جو A k FN، k نقاط داده را در P با بیشترین فاصله جمعی تا تمام نقاط پرس و جو در Q با توجه به مجموعه ای از نقاط داده P و مجموعه ای از نقاط پرس و جو Q ، بازیابی می کند . در شبکه‌های فضایی، راه‌حل‌های مؤثری برای پرسش‌های A k FN پیشنهاد شد [ ۱۱ ].

با توجه به تفاوت در ویژگی‌های بین کوتاه‌ترین فاصله مسیر و فاصله اقلیدسی، راه‌حل‌های موجود مبتنی بر فضای اقلیدسی را نمی‌توان مستقیماً برای پاسخگویی به جستارهای پیوستن k FN در شبکه‌های فضایی استفاده کرد. راه‌حل‌های موجود برای جستجوی نزدیک‌ترین همسایه [ ۲۷ ، ۲۸ ، ۲۹ ] نمی‌توانند به راحتی برای رسیدگی به مشکلات جستجوی دورترین همسایه به دلیل ویژگی‌های فاصله متفاوت بین دور و نزدیک استفاده شوند. اگرچه محاسبات گروهی پرس و جوهای فضایی توجه قابل توجهی را به خود جلب کرده است [ ۱۹ , ۲۷ , ۳۰ , ۳۱ , ۳۲ , ۳۳ , ۳۴]، محاسبات گروهی برای k جستارهای پیوستن FN برای شبکه های فضایی اعمال نشده است. برای پردازش موثر k پرس و جوهای پیوستن FN در شبکه های فضایی، الگوریتم های پیچیده جدیدی باید توسعه داده شوند. اول، اتصال k FN طبق تعریف یک عملیات پرهزینه است. دوم، جستجوی دورترین همسایه دشوارتر از جستجوی نزدیکترین همسایه است. در نهایت، طراحی ساختارهای شاخص که به طور موثر از جستجوی FN برای شبکه‌های فضایی پشتیبانی می‌کنند، دشوار است. از نظر حوزه فضا، نوع پرس و جو و نوع داده، جدول ۱ سناریوی مشکل ما را با مطالعات موجود مقایسه می کند.

۲٫۲٫ علامت گذاری و تشریح مشکل رسمی

نقاط پرس و جو و داده در یک شبکه فضایی G قرار می گیرند و این نقاط نشان دهنده نقاط مورد علاقه (POI) هستند، همانطور که در شکل ۱ نشان داده شده است. با توجه به دو نقطه q و p ، طول کوتاه ترین مسیر بین q و p در G است. جدول ۲ نمادهای مورد استفاده در این مطالعه را خلاصه می کند.

تعریف ۱٫

جستجوی kFN [ ۶ ، ۷ ، ۸ ، ۹ ، ۱۰ ، ۱۱ ، ۱۳ ، ۱۴ ]. با در نظر گرفتن یک عدد صحیح مثبت k، یک نقطه پرس و جو q، و یک مجموعه P از نقاط داده، نقطه پرس و جو q مجموعه ای از k نقطه داده را برمی گرداند که به صورت نشان داده می شوند. ، به طوری که نگه می دارد برای و .

تعریف ۲٫

kFN ملحق شود. با در نظر گرفتن یک عدد صحیح مثبت k، مجموعه ای از نقاط پرس و جو Q، و مجموعه ای از نقاط داده P، پرس و جو پیوستن kFN، به عنوان نشان داده شده است. ، جفت های مرتب شده از هر نقطه پرس و جو q را در Q و مجموعه ای از k نقطه داده دورتر از q را برمی گرداند. برای سادگی، به اختصار به ، که به طور رسمی توسط . توجه داشته باشید که اتصالات kFN جابجایی نیستند، به عنوان مثال، .

تعریف ۳٫

شبکه فضایی [ ۳۲ ، ۳۳ ، ۳۶ ، ۳۷ ، ۳۸ ]. یک نمودار وزنی بدون جهت برای نمایش یک شبکه فضایی استفاده می شود که در آن V، E و W به ترتیب مجموعه راس، مجموعه یال و ماتریس فاصله لبه را نشان می دهند. هر لبه دارای وزن غیر منفی است که فاصله شبکه را نشان می دهد.

تعریف ۴٫

راس های تقاطع، میانی و انتهایی. رئوس را می توان بر اساس درجه آنها به سه دسته تقسیم کرد: (۱) اگر درجه یک راس بزرگتر یا مساوی ۳ باشد، راس به عنوان راس تقاطع شناخته می شود. (۲) اگر درجه ۲ باشد، راس یک راس میانی است. (۳) اگر درجه ۱ باشد، راس یک راس انتهایی است.

تعریف ۵٫

دنباله رأس، بخش پرس و جو و بخش داده. یک دنباله رأس نشان دهنده مسیری بین دو رأس است، و ، به طوری که و یا یک راس تقاطع هستند یا یک راس انتهایی، و رئوس دیگر در مسیر، ، رئوس میانی هستند. یک بخش پرس و جو نشان دهنده بخش خطی است که نقاط پرس و جو را به هم متصل می کند و یک بخش داده نشان دهنده یک پاره خط است که نقاط داده را به هم متصل می کند . برای سادگی، و به اختصار به و به ترتیب برای کاهش سردرگمی.

۳٫ خوشه بندی نقاط و محاسبه فاصله ها

در بخش ۳٫۱ ، نقاط پرس و جو (نقاط داده) را با استفاده از اتصال شبکه فضایی گروه بندی می کنیم. ما حداکثر و حداقل فاصله بین یک نقطه مرزی و یک خوشه داده را در بخش ۳٫۲ محاسبه می کنیم.

۳٫۱٫ خوشه بندی پرس و جو و نقاط داده با استفاده از اتصال شبکه فضایی

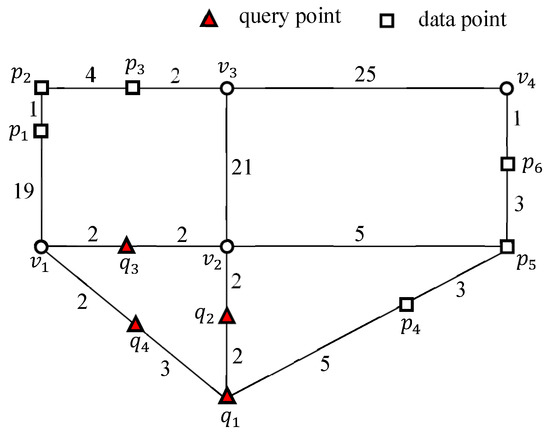
شکل ۲ نمونه ای از اتصال k FN را نشان می دهد ، جایی که ، ، و داده می شود. مثال K FN پرس و جو پیوستن مستلزم آن است که هر نقطه پرس و جو q در Q دو نقطه داده دورتر از q را پیدا کند.

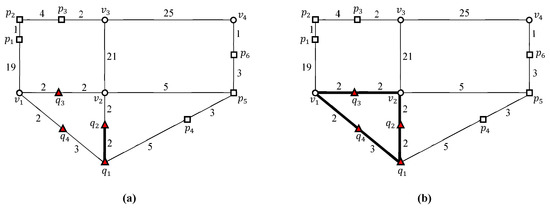
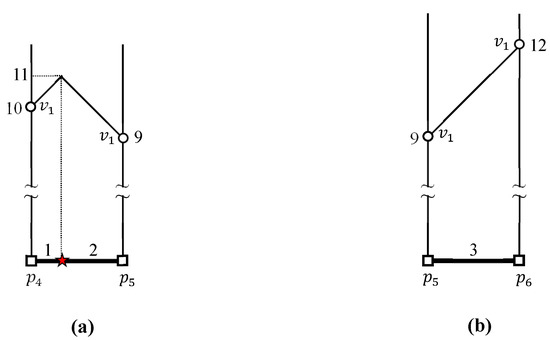
شکل ۳ نمونه‌ای از روش خوشه‌بندی دو مرحله‌ای را برای گروه‌بندی نقاط پرس و جوی نزدیک به خوشه‌های پرس و جو نشان می‌دهد. یک قطعه پرس و جو در مرحله اول با اتصال نقاط پرس و جو در یک دنباله راس ایجاد می شود. در شکل ۳ الف، نقاط پرس و جو و در یک دنباله راس متصل هستند تا تبدیل شوند . بنابراین، سه بخش پرس و جو ، ، و همانطور که در شکل ۳ الف نشان داده شده است، تولید می شوند. در مرحله دوم، از یک راس تقاطع برای اتصال بخش های پرس و جو مجاور برای تشکیل یک خوشه پرس و جو استفاده می شود. در شکل ۳ ب، راس تقاطع دو بخش پرس و جو را به هم متصل می کند و . به همین ترتیب، و توسط راس تقاطع به هم مرتبط می شوند . سرانجام، و توسط راس تقاطع به هم مرتبط می شوند . در نتیجه، سه بخش پرس و جو ، ، و برای تشکیل یک خوشه پرس و جو پیوند داده شده اند . توجه داشته باشید که یک خوشه پرس و جو مجموعه ای از بخش های پرس و جو است. طبیعتا مجموعه ای از نقاط پرس و جو به مجموعه ای از خوشه های پرس و جو تبدیل می شود . اجازه دهید یک نقطه مرزی برای یک خوشه پرس و جو تعریف کنیم . هنگامی که یک خوشه پرس و جو و خوشه nonquery آن در یک نقطه ملاقات کنید، آن نقطه به عنوان نقطه مرزی نامیده می شود . در این مثال، سه نقطه مرزی ، ، و برای یافت می شوند . بنابراین، مجموعه ای از نقاط مرزی از توسط .

شکل ۴ نمونه ای از روش خوشه بندی دو مرحله ای را برای گروه بندی نقاط داده مجاور در خوشه های داده نشان می دهد. قابل ذکر است که پرس و جو و نقاط داده با استفاده از روش دو مرحله ای یکسان خوشه بندی می شوند. در مرحله اول، نقاط داده ، ، و در یک دنباله راس برای تبدیل شدن به یک بخش داده متصل می شوند . به طور مشابه، نقاط داده و در یک دنباله راس برای تشکیل یک بخش داده پیوند داده شده اند . در نتیجه، سه بخش داده ، ، و همانطور که در شکل ۴ الف نشان داده شده است، تولید می شوند. در مرحله دوم، دو بخش داده و توسط یک راس تقاطع به هم می پیوندند برای تشکیل یک خوشه داده . در نتیجه مجموعه ای از نقاط داده به مجموعه ای از خوشه های داده تبدیل می شود .

۳٫۲٫ محاسبه حداکثر و حداقل فاصله از یک نقطه مرزی تا یک خوشه داده

حداکثر و حداقل فاصله بین یک نقطه مرزی و یک خوشه داده در این بخش محاسبه می شوند. حداقل و حداکثر فاصله بین و به طور رسمی توسط و ، به ترتیب. حداقل فاصله بین و را می توان به راحتی محاسبه کرد جایی که نقطه مرزی یک خوشه داده است . حداکثر فاصله بین و را می توان توسط جایی که حداکثر فاصله بین است و یک بخش داده که در .

یک مثال برای نشان دادن نحوه محاسبه حداکثر و حداقل فاصله بین یک نقطه مرزی استفاده می شود و یک خوشه داده . توجه داشته باشید که پرس و جو پیوستن k FN به عنوان مثال دارای سه نقطه مرزی و دو خوشه داده است، به عنوان مثال، و . در این بخش حداکثر و حداقل فاصله بین و محاسبه می شوند، جایی که و . توجه داشته باشید که محاسبات از ، ، ، ، ، و به ترتیب در شکل ۵ ، شکل ۶ ، شکل ۷ ، شکل ۸ ، شکل ۹ و شکل ۱۰ نشان داده شده است.

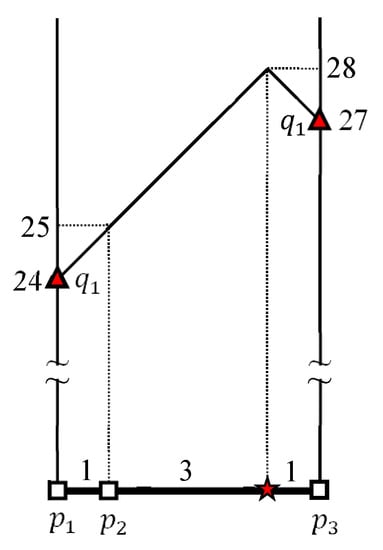
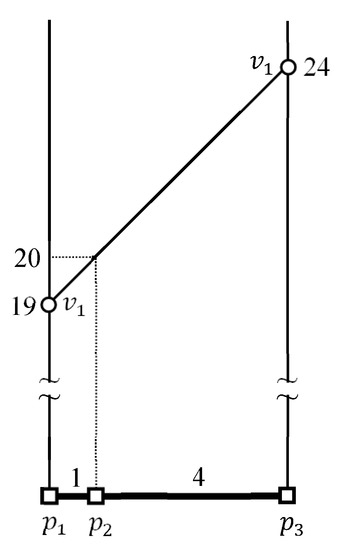
شکل ۵ محاسبات را نشان می دهد . اول، فواصل از به نقاط پایانی و از ارزیابی به و ، به ترتیب. یک نقطه p را در نظر بگیرید . زیرا p در آن نهفته است ، که طول آن است ، فاصله بین و p توسط . اجازه دهید برای . سپس، ما داریم زیرا . می توانیم بازنویسی کنیم برای . همانطور که در شکل ۵ نشان داده شده است ، حداکثر و حداقل فاصله بین و است و ، به ترتیب. برای راحتی، نماد ستاره (★) در شکل ۵ برای نشان دادن مشخص شده است .

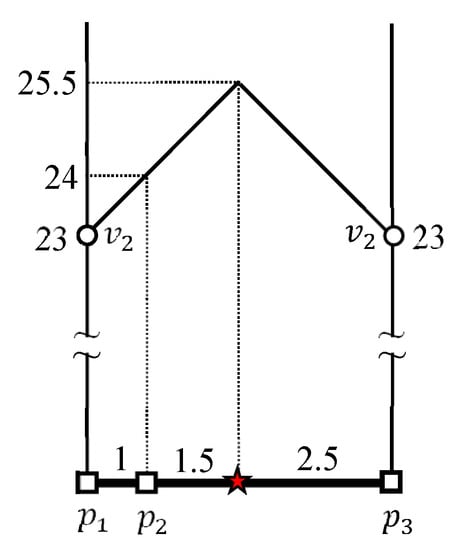
حداکثر فاصله بین یک نقطه مرزی و یک خوشه داده توسط . محاسبات از و به ترتیب در شکل ۶ a,b نشان داده شده است. فواصل از به نقاط پایانی و هستند و ، به ترتیب. حداکثر و حداقل فاصله از به در شکل ۶ الف به صورت نشان داده شده است و ، به ترتیب. فواصل از به نقاط پایانی و از هستند و ، به ترتیب. حداکثر و حداقل فاصله از به محاسبه می شود و به ترتیب، همانطور که در شکل ۶ ب نشان داده شده است. بنابراین حداکثر و حداقل فاصله بین و هستند و ، به ترتیب.

شکل ۷ محاسبات را نشان می دهد و . فواصل از به نقاط پایانی و از هستند و ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب.

شکل ۸ محاسبات را نشان می دهد و . حداکثر فاصله بین و محاسبه می شود . محاسبات از و به ترتیب در شکل ۸ a,b نشان داده شده است. فواصل از به نقاط پایانی و از هستند و ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و به ترتیب، همانطور که در شکل ۸ a نشان داده شده است، جایی که نماد ستاره (★) برای نشان دادن علامت گذاری شده است. . فواصل از به نقاط پایانی و از هستند و ، به ترتیب. همانطور که در شکل ۸ ب نشان داده شده است، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب.

شکل ۹ محاسبات را نشان می دهد و . فواصل از به نقاط پایانی و از هستند ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب. توجه داشته باشید که علامت ستاره (★) در شکل ۹ برای نشان دادن علامت گذاری شده است .

شکل ۱۰ محاسبات را نشان می دهد و . حداکثر فاصله بین و محاسبه می شود . محاسبات از و به ترتیب در شکل ۱۰ a,b نشان داده شده است. فواصل از به نقاط پایانی و از هستند و ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب، همانطور که در شکل ۱۰ نشان داده شده است. فواصل از به نقاط پایانی و از هستند و ، به ترتیب. بنابراین، حداکثر و حداقل فاصله بین و هستند و به ترتیب، همانطور که در شکل ۱۰ نشان داده شده است. بنابراین، حداکثر و حداقل فاصله بین و هستند و ، به ترتیب.

جدول ۳ حداکثر و حداقل فاصله بین نقاط مرزی را خلاصه می کند و خوشه های داده در .

۴٫ الگوریتم پیوستن حلقه تودرتو برای شبکه های فضایی

الگوریتم CNLJ در بخش ۴٫۱ توضیح داده شده است . بخش ۴٫۲ k پرس و جوهای FNs را در نقاط مرزی خوشه های پرس و جو ارزیابی می کند. در نهایت، مثال K FNs Join Query در بخش ۴٫۳ ارزیابی می‌شود .

۴٫۱٫ الگوریتم پیوستن حلقه تودرتو به خوشه

الگوریتم CNLJ در الگوریتم ۱ توضیح داده شده است که شامل دو مرحله است. روش خوشه بندی دو مرحله ای (خطوط ۲-۴)، که در بخش ۳٫۱ توضیح داده شده است، برای گروه بندی نقاط پرس و جو در نزدیکی (نقاط داده) به خوشه های پرس و جو (خوشه های داده) در مرحله اول استفاده می شود. در مرحله دوم، اتصال k FN برای هر خوشه پرس و جو انجام می شود (خطوط ۵-۸). در نهایت، نتیجه پیوستن k FN هنگامی که پیوستن k FN برای هر خوشه پرس و جو تکمیل شود، به کاربر پرس و جو برگردانده می شود (خط ۹).

الگوریتم ۱ CNLJ( ).

ورودی: k : تعداد FN برای q ، Q : مجموعه نقاط پرس و جو، و P : مجموعه نقاط داده
خروجی: : مجموعه ای از جفت های مرتب شده از هر نقطه پرس و جو q در Q و مجموعه ای از k FN برای q ، به عنوان مثال، .

۱:: // مجموعه نتایج به مجموعه خالی مقدار دهی اولیه می شود.
۲:: // مرحله ۱: پرس و جو و نقاط داده خوشه بندی می شوند که در بخش ۳٫۱ ارائه شده است .
۳:: // نقاط پرس و جو در خوشه های پرس و جو گروه بندی می شوند.
۴:: // نقاط داده در خوشه های داده گروه بندی می شوند.
۵:: // مرحله ۲: اتصال k FN برای هر خوشه پرس و جو انجام می شود که در الگوریتم ۲ ارائه شده است.
۶:: برای هر خوشه پرس و جو انجام دادن
۷:: // .
۸:: // نتیجه پیوستن k FN برای به اضافه می شود .
۹:: برگشت // پس از پیوستن k FN برای هر خوشه پرس و جو برگردانده می شود کامل است.

الگوریتم ۲ الگوریتم پیوستن k FN را برای یک خوشه پرس و جو توصیف می کند . ابتدا k پرس و جوهای FN در نقاط مرزی ارزیابی می شوند برای جمع آوری نقاط داده کاندید برای نقاط پرس و جو در (خطوط ۴-۷)، که در الگوریتم ۳ توضیح داده شده است. سپس، هر پرس و جو نقطه q در k FN ها را برای q در میان نقاط داده کاندید در بازیابی می کند (خطوط ۸-۱۱)، که در الگوریتم ۴ به تفصیل آمده است. در نهایت، نتیجه پیوستن k FN برای نقاط پرس و جو در بعد از هر نقطه پرس و جو q in برگردانده می شود k FN را برای q از نقاط داده کاندید بازیابی می کند (خط ۱۲).

الگوریتم ۲ .

ورودی: k : تعداد FN برای q ، : خوشه پرس و جو و : مجموعه ای از خوشه های داده
خروجی: : مجموعه ای از جفت های مرتب شده از هر نقطه پرس و جو q in و مجموعه ای از k FN برای q ، به عنوان مثال،

۱:: // مجموعه نتیجه برای نقاط پرس و جو در به مجموعه خالی مقدار دهی اولیه می شود.
۲:: // توجه داشته باشید که .
۳:: // l حداکثر فاصله بین نقاط مرزی را نشان می دهد .
۴:: // مرحله ۱: k پرس و جو FN در هر نقطه مرزی ارزیابی می شود که در
۵:: برای هر نقطه مرزی انجام دادن
۶:: // k پرس و جو FN در ارزیابی می شود که در الگوریتم ۳ به تفصیل آمده است.
۷:: // نقاط داده کاندید را برای نقاط پرس و جو جمع آوری می کند .
۸:: // مرحله ۲: هر نقطه پرس و جو q k FN را در بین نقاط داده کاندید در آن بازیابی می کند .
۹:: برای هر نقطه پرس و جو انجام دادن
۱۰:: // مجموعه ای از نقاط داده کاندید برای q است.
۱۱:
۱۲:: برگشت // هنگامی که جستجوی k FN برای هر نقطه پرس و جو انجام شود ، برگردانده می شود .

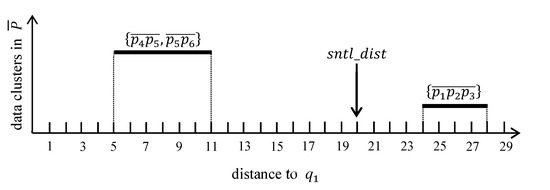
الگوریتم ۳ الگوریتم پردازش پرس و جو k FN را برای یافتن نقاط داده کاندید در یک نقطه مرزی توصیف می کند. برای یک خوشه پرس و جو توجه داشته باشید که نتیجه پرس و جو k FN برای شامل نقاط داده کاندید برای نقاط پرس و جو در . مجموعه k FN برای ، ، به مجموعه خالی مقدار دهی اولیه می شود (خط ۱). آرگومان سوم l حداکثر فاصله بین نقاط مرزی را نشان می دهد ، یعنی . فاصله نگهبان به مقدار دهی اولیه می شود و تعیین می کند که آیا یک نقطه داده p یک نقطه نامزد برای آن است یا خیر . حداکثر و حداقل فاصله از به خوشه های داده در همانطور که در بخش ۳٫۲ توضیح داده شد، محاسبه می شوند . سپس خوشه های داده به ترتیب کاهش حداکثر فاصله آنها مرتب می شوند . به طور طبیعی، خوشه های داده مرتب شده به صورت متوالی بررسی می شوند. اگر حداکثر فاصله از به خوشه داده برای کاوش بعدی کوچکتر از فاصله نگهبان است، به عنوان مثال، ، نیازی به بررسی خوشه های داده ناشناخته باقیمانده نیست زیرا نقاط داده در این خوشه های داده می توانند نقاط داده کاندید برای هیچ نقطه پرس و جو باشند. . در غیر این صورت (یعنی )، هر نقطه داده p in باید بررسی شود تا مشخص شود آیا p یک نقطه کاندید برای نقاط پرس و جو است یا خیر . برای این، محاسبه می شود. اگر درونش است ، سپس فاصله از به p به سادگی با استفاده از یک الگوریتم جستجوی نمودار مانند الگوریتم Dijkstra [ ۳۹ ] محاسبه می شود. در غیر این صورت (یعنی اگر بیرون است )، فاصله به ارزیابی می شود . توجه داشته باشید که نقطه مرزی است و نقطه مرزی است . این به این دلیل است که اگر بیرون است ، کوتاه ترین مسیر از به p باید از یک نقطه مرزی عبور کند از ، یعنی . اگر ، سپس p به آن اضافه می شود به عنوان یک نقطه داده کاندید برای . نقاط داده اضافی p ممکن است در آن گنجانده شود و باید از آنها حذف شوند . بنابراین، هر نقطه داده p در برای تأیید اینکه p واجد شرایط بودن یک نقطه داده کاندید است، بررسی می شود، به عنوان مثال، . اگر p واجد شرایط نباشد، از آن حذف می شود . در نهایت، اگر حداکثر فاصله از به خوشه داده کوچکتر از فاصله نگهبان است (خطوط ۱۰-۱۲) یا اگر هر خوشه داده بررسی شود، نتیجه پرس و جو k FN برای ، ، برگردانده می شود.

الگوریتم ۳ .

ورودی: k : تعداد FN برای q ، l : حداکثر فاصله بین نقاط مرزی در ، : نقطه مرزی ، و : مجموعه ای از خوشه های داده
خروجی: : مجموعه ای از k FN برای

۱:: // مجموعه ای از k FN برای یک نقطه مرزی ، ، به مجموعه خالی مقدار دهی اولیه می شود.
۲:: // t = فاصله نگهبان به ۰ مقداردهی اولیه می شود.
۳:: // حداکثر و حداقل فاصله از به خوشه های داده در همانطور که در بخش ۳٫۲ توضیح داده شد محاسبه می شوند .
۴:: برای هر خوشه داده انجام دادن
۵:: محاسبه کنید و
۶:: // خوشه های داده در به ترتیب کاهش حداکثر فاصله آنها تا مرتب شده اند
۷:: ) // شامل خوشه های داده مرتب شده برای .
۸:: // خوشه های داده به صورت متوالی بررسی می شوند.
۹:: برای هر خوشه داده مرتب شده انجام دادن
۱۰:: اگر سپس
۱۱:: // توجه داشته باشید که همانطور که در خط ۲۴ نشان داده شده است به روز می شود.
۱۲:: به خط ۲۶ بروید // این بدان معنی است که دیگر خوشه های داده نیازی به کاوش ندارند.
۱۳:: // هر نقطه داده p in به طور متوالی برای یافتن k FN برای .
۱۴:: برای هر نقطه داده انجام دادن
۱۵:: // با استفاده از دو حالت زیر محاسبه می شود. و .
۱۶:: اگر درونش است سپس
۱۷:: به سادگی با استفاده از یک الگوریتم جستجوی نمودار مانند الگوریتم Dijkstra [ ۳۹ ] محاسبه می شود.
۱۸:: دیگر
۱۹:: // توجه داشته باشید که مسیر از به p است .
۲۰:: // p به اضافه می شود اگر .
۲۱:: اگر سپس
۲۲:: // نقاط داده کاندید را برای نقاط پرس و جو جمع آوری می کند .
۲۳:: // p به اضافه می شود .
۲۴:: // k امین FN فعلی است .
۲۵:: // نقاط داده اضافی p حذف می شوند زیرا آنها می توانند k FN بدون نقطه پرس و جو باشند
۲۶:: برای هر نقطه داده انجام دادن
۲۷:: اگر سپس
۲۸:: // p هیچ نقطه داده کاندیدایی برای آن نیست و از آن حذف می شود .
۲۹:: برگشت // پس از جمع آوری نقاط داده کاندید برای نقاط پرس و جو در آن بازگردانده می شود .

الگوریتم ۴ توضیح می دهد که یک نقطه پرس و جو q در k FN را برای q در بین نقاط داده کاندید در بازیابی می کند . اولین، به مجموعه خالی مقدار دهی اولیه می شود. فاصله بین q و نقطه داده کاندید p با استفاده از دو حالت زیر محاسبه می شود: و . اگر p داخل باشد ، یعنی سپس فاصله q تا p به سادگی با استفاده از الگوریتم جستجوی نمودار [ ۳۹ ] محاسبه می شود. در غیر این صورت (یعنی )، فاصله به ارزیابی می شود . این به این دلیل است که کوتاه ترین مسیر از q تا p باید از یک نقطه مرزی عبور کند از ، یعنی . چه زمانی محاسبه می شود، دو شرط زیر برای تعیین اینکه آیا نقطه داده p به آن اضافه شده است بررسی می شود : اگر کاردینالیته از کوچکتر از k است، یعنی، ، سپس p به سادگی به آن اضافه می شود . به علاوه، اگر p از q دورتر از k th FN فعلی باشد از q ، یعنی، ، سپس p به آن اضافه می شود و از حذف می شود . در نهایت، هنگامی که کاوش هر نقطه داده کاندید کامل شد، نتیجه پرس و جو k FN برای q ، ، برگردانده می شود.

الگوریتم ۴ .

ورودی: k : تعداد FN برای q ، q : نقطه پرس و جو در ، : مجموعه ای از نقاط داده کاندید برای خروجی q :
: مجموعه ای از k FN برای q

۱:: // به مجموعه خالی مقدار دهی اولیه می شود.
۲:: // مجموعه ای از نقاط داده کاندید برای q است.
۳:: برای هر نقطه داده کاندید انجام دادن
۴:: اگر p داخل باشد سپس
۵:: به سادگی با استفاده از یک الگوریتم جستجوی نمودار مانند الگوریتم Dijkstra محاسبه می شود [ ۳۹ ]
۶:: دیگر
۷:: //توجه داشته باشید که در الگوریتم ۳ محاسبه شد.
۸:: // p به اضافه می شود اگر یکی از دو شرط زیر را برآورده کند.
۹:: اگر سپس
۱۰:
۱۱:: دیگر اگر و سپس
۱۲:: // توجه داشته باشید که k th FN فعلی q است.
۱۳:
۱۴:: برگشت

لم ۱ ثابت می کند که یک نقطه پرس و جو q در یک خوشه پرس و جو می تواند k FN را برای q در بین نقاط داده کاندید در بازیابی کند .

لم ۱٫

هر نقطه پرس و جو q در یک خوشه پرس و جو می تواند k FN را برای q در بین نقاط داده کاندید در بازیابی کند .

اثبات

لم ۱ با تناقض ثابت می شود. برای این، فرض کنید که یک نقطه داده واجد شرایط p در وجود دارد و آن p به آن تعلق ندارد ، یعنی و . نقطه داده واجد شرایط p از q دورتر از k امین FN است نقطه مرزی از ، که به این معنی است . با توجه به الگوریتم ۳، آن را حفظ می کند و ، جایی که . بنابراین فاصله q تا p از طریق کوچکتر از فاصله از به ، یعنی . این بخاطر این است که و داده می شود. به وضوح، دلالت دارد . این منجر به تناقض با این فرض می شود که . بنابراین، هر پرس و جو نقطه q در یک خوشه پرس و جو می تواند k FN را برای q در بین نقاط داده کاندید در بازیابی کند . □

همانطور که در جدول ۴ نشان داده شده است، الگوریتم های CNLJ و اتصال غیر خوشه ای برای شبکه های فضایی پیچیدگی های زمانی متفاوتی دارند . قابل توجه است که الگوریتم CNLJ متعامد به الگوریتم های پردازش پرس و جو k FN است که به راحتی می تواند در الگوریتم CNLJ گنجانده شود. راه حل ساده برای یافتن k FN برای یک نقطه پرس و جو در این تحلیل برای سادگی استفاده می شود. پیچیدگی زمانی پردازش پرس و جو k FN است . الگوریتم CNLJ حداکثر ارزیابی می کند k جستارهای FN، که در آن M حداکثر تعداد نقاط مرزی یک خوشه پرس و جو است ، یعنی . الگوریتم پیوستن غیر خوشه ای به سادگی ارزیابی می کند k پرس و جوهای FN زیرا k پرس و جوهای FN برای نقاط پرس و جو باید به صورت متوالی ارزیابی شوند. بنابراین، پیچیدگی‌های زمانی الگوریتم‌های پیوستن CNLJ و غیر خوشه‌ای هستند و ، به ترتیب. نتایج نظری نشان می دهد که الگوریتم CNLJ سریعتر از الگوریتم پیوستن غیر خوشه ای اجرا می شود، به ویژه زمانی که ، به عنوان مثال، نقاط پرس و جو به طور متراکم خوشه ای هستند. علاوه بر این، نتایج حاکی از آن است که الگوریتم CNLJ عملکردی مشابه الگوریتم پیوستن غیر خوشه‌ای را نشان می‌دهد. ، یعنی نقاط پرس و جو خوشه بندی نشده اند.

۴٫۲٫ ارزیابی k پرس و جوهای FN در نقاط مرزی

الگوریتم CNLJ k پرس و جوهای FN را در نقاط مرزی خوشه های پرس و جو ارزیابی می کند. . برای مثال K FN Join Query، الگوریتم CNLJ k پرس و جوهای FN را در نقاط مرزی ارزیابی می کند. ، ، و ، به جای نقاط پرس و جو ، ، ، و . ابتدا کوئری k FN در یک نقطه مرزی ارزیابی می شود . حداکثر و حداقل فاصله بین و هر خوشه داده در محاسبه می شوند و خوشه های داده بر اساس حداکثر فاصله آنها به ترتیب نزولی مرتب می شوند . همانطور که در شکل ۱۱ نشان داده شده است ، دو خوشه داده و با استفاده از حداکثر فاصله آنها مرتب شده اند به شرح زیر است: . این بخاطر این است که و همانطور که در جدول ۳ توضیح داده شده است. نقطه مرزی بررسی می کند به دنبال . در پی کاوش در ، انتخاب می کند و به عنوان دو FN به دلیل ، ، و همانطور که در شکل ۵ نشان داده شده است، محاسبه می شوند . فاصله نگهبان برای است . این به این دلیل است که حداکثر فاصله l بین نقاط مرزی در است ، در حالی که فاصله از به FN دوم خود است . بنابراین، مجموعه ای از نقاط داده کاندید برای نقاط پرس و جو در است . این بخاطر این است که ، ، و . به وضوح، دیگر خوشه داده دیگر را بررسی نمی کند . این بخاطر این است که بزرگتر از جایی که همانطور که در جدول ۳ نشان داده شده است. در نهایت، مجموعه ای از نقاط داده کاندید برای نقاط پرس و جو در است .

در سایر نقاط مرزی و ، می توانیم به طور مشابه k پرس و جوهای FN را ارزیابی کنیم. دو FN از هستند و همانطور که در شکل ۷ و شکل ۸ نشان داده شده است. بنابراین، مجموعه ای از داده های نامزد به نشان می دهد است زیرا فاصله نگهبان برای است . به طور مشابه، دو FN از هستند و همانطور که در شکل ۹ و شکل ۱۰ نشان داده شده است. بنابراین، مجموعه ای از داده های نامزد به نشان می دهد است زیرا فاصله نگهبان برای است . جدول ۵ مجموعه ای از نقاط داده کاندید را برای نقاط مرزی خلاصه می کند ، ، و و فاصله نگهبان آنها

۴٫۳٫ ارزیابی یک مثال k FN Join Query

الگوریتم CNLJ برای هر نقطه پرس و جو، k FN را بازیابی می کند در میان نقاط داده کاندید در . این مثال k پرس و جو پیوستن FN به دو FN برای هر نقطه پرس و جو نیاز دارد، به عنوان مثال، ، و مجموعه ای از نقاط داده کاندید است . هر کدام از ، ، ، و دو FN خود را در بین نقاط داده کاندید بازیابی می کند ، ، و . دو FN از ابتدا دو FN از بعد تعیین می شوند و غیره. اجازه دهید دو FN برای آن پیدا کنیم در میان نقاط داده نامزد ، ، و . فواصل از به ، ، و باید با استفاده از این واقعیت محاسبه شود که کوتاهترین مسیر از به یک نقطه داده کاندید باید از یک نقطه مرزی عبور کند . در نتیجه طول کوتاه ترین مسیر از به برابر است با . فاصله از به ارزیابی می کند . فاصله از به ارزیابی می کند . بدین ترتیب، و دو FN برای که مجموعه نتایج آن است . بعد، دو FN برای در میان نقاط داده کاندید بازیابی می شوند ، ، و . برای این، فواصل از به ، ، و باید محاسبه شود. همانطور که در جدول ۶ نشان داده شده است ، فواصل از به ، ، و ارزیابی به ، ، و ، به ترتیب. بدین ترتیب، و دو FN برای ، که مجموعه نتایج آن است . به طور مشابه، دو FN برای و را می توان در میان نقاط داده کاندید بازیابی کرد ، ، و . جدول ۶ فاصله یک نقطه پرس و جو q تا یک نقطه داده کاندید p را محاسبه می کند و دو FN برای q در بین نقاط داده کاندید بازیابی می کند. و . در نهایت، نتیجه پیوستن k FN مجموعه اتحادیه نتایج جستجوی k FN برای نقاط پرس و جو در Q به شرح زیر است: .

۵٫ ارزیابی عملکرد

الگوریتم CNLJ و رقبای آن به صورت تجربی در این بخش تحت شرایط مختلف مقایسه شده اند. بخش ۵٫۱ شرایط آزمایشی را شرح می دهد و بخش ۵٫۲ نتایج آزمایش را گزارش می کند.

۵٫۱٫ تنظیمات آزمایشی

جدول ۷ دو نقشه راه واقعی [ ۴۰ ] را توصیف می کند که در آزمایش ها استفاده شد. این نقشه‌های راه واقعی اندازه‌های مختلفی دارند و بخشی از شبکه جاده‌ای ایالات متحده هستند. برای راحتی، جهان داده به یک مربع واحد از صفحه نرمال شد. نقاط پرس و جو و داده برای تقلید از توزیع های بسیار اریب POI در دنیای واقعی ایجاد شدند. اول، مرکزها به طور تصادفی در داخل جهان داده انتخاب شدند، جایی که m تعداد کل مرکزها را نشان می دهد و بین ۱ تا ۱۰ متغیر است. پرس و جو و نقاط داده در اطراف هر مرکز توزیع نرمال را نشان می دهند، با میانگین نشان دهنده مرکز و انحراف استاندارد تنظیم شده است. . جدول ۸ تنظیمات پارامترهای آزمایشی را نشان می دهد. ما در هر آزمایش یک پارامتر واحد را در محدوده تغییر دادیم در حالی که پارامترهای دیگر را در مقادیر پیش‌فرض پررنگ حفظ کردیم.

الگوریتم پایه، که یک الگوریتم اتصال غیر خوشه‌ای برای محاسبه متوالی k FNs هر نقطه پرس و جو در Q است، به عنوان معیاری برای ارزیابی الگوریتم CNLJ استفاده شد. ما دو نسخه از راه حل پیشنهادی خود، یعنی CNLJ را پیاده سازی و ارزیابی کردیم و CNLJ . نسخه ساده لوح به نام CNLJ از الگوریتم CNLJ نقاط پرس و جو را در بخش های پرس و جو گروه بندی می کند، همانطور که در شکل ۳ الف نشان داده شده است. بنابراین، CNLJ حداکثر دو k پرس و جو FN را برای یک بخش پرس و جو ارزیابی می کند. نسخه بهینه شده به نام CNLJ از الگوریتم CNLJ، نقاط پرس و جو را با استفاده از روش خوشه بندی دو مرحله ای، همانطور که در شکل ۳ ب نشان داده شده است، در خوشه های پرس و جو گروه بندی می کند. توجه داشته باشید که کدهای منبع برای ارزیابی تجربی این مطالعه از طریق سایت GitHub در https://github.com/Hyung-Ju-Cho/ (در ۸ فوریه ۲۰۲۱ قابل دسترسی است). در محیط توسعه Microsoft Visual Studio 2019، همه الگوریتم‌های Join در C++ پیاده‌سازی شدند. همه زیربرنامه های رایج الگوریتم ها برای کارهای مشابه مجددا استفاده شدند. آزمایش ها بر روی یک کامپیوتر رومیزی با سیستم عامل ویندوز ۱۰ با ۳۲ گیگابایت رم و یک پردازنده ۸ هسته ای (i9-9900) با فرکانس ۳٫۱ گیگاهرتز انجام شد. همانطور که در چندین مطالعه موجود [ ۳۶ ، ۴۱] برای خدمات نقشه آنلاین، این مطالعه تجربی فرض می‌کند که تمام ساختارهای نمایه‌سازی الگوریتم‌ها در حافظه اصلی برای ارزیابی سریع جستارهای پیوستن k FN باقی می‌مانند. میانگین زمان مورد نیاز برای پاسخ دادن به k پرس و جوهای پیوستن FN از طریق آزمایش های مکرر با استفاده از k پرس و جوهای پیوستن FN محاسبه شد. در نهایت، فاصله شبکه بین دو نقطه را به سرعت با استفاده از روش TNR محاسبه کردیم [ ۴۲ ]. این به این دلیل است که روش TNR پیاده سازی آسان است و عملکرد قابل مقایسه با سایر الگوریتم های کوتاه ترین فاصله را نشان می دهد [ ۳۸ ، ۴۱ ، ۴۳ ، ۴۴ ، ۴۵ ].

۵٫۲٫ نتایج تجربی

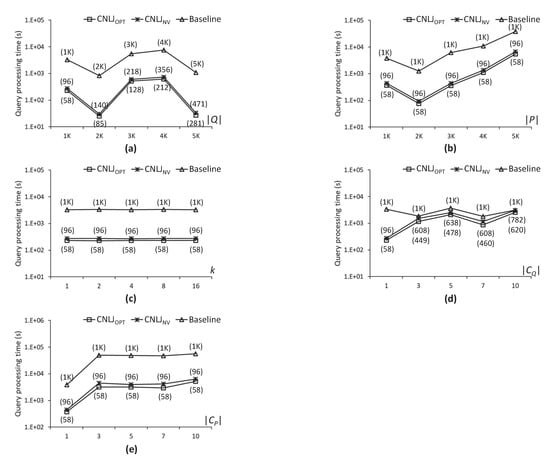
CNLJ پیشنهادی ، CNLJ و الگوریتم های پایه در نقشه راه NA در شکل ۱۲ مقایسه شده اند . هر نمودار زمان پردازش پرس و جو پیوستن k FN و تعداد k پرس و جوهای FN مورد نیاز برای ارزیابی جستار k FN را نشان می دهد. تعداد k پرس و جوهای FN مورد نیاز CNLJ ، CNLJ و الگوریتم های پایه برای پاسخ به جستار پیوستن k FN در پرانتز در شکل ۱۲ ، شکل ۱۳ و شکل ۱۴ نشان داده شده است. توجه داشته باشید که CNLJ الگوریتم k پرس و جوهای FN را در نقاط مرزی خوشه های پرس و جو، CNLJ ارزیابی می کند. الگوریتم k پرس و جوهای FN را در نقاط انتهایی بخش های پرس و جو ارزیابی می کند، و الگوریتم پایه، k پرس و جوهای FN را در نقاط پرس و جو ارزیابی می کند. در نتیجه، الگوریتم پایه همان تعداد k پرس‌و‌جوی FN را به عنوان عدد ارزیابی می‌کند از نقاط پرس و جو در Q شکل ۱۲ a زمان پردازش پرس و جو CNLJ را نشان می دهد ، CNLJ و الگوریتم های پایه زمانی که تعداد نقاط پرس و جو بین ۱۰۰۰ تا ۵۰۰۰ تغییر کند، به عنوان مثال، . در تمام موارد در ، CNLJ الگوریتم سریعتر از CNLJ است و الگوریتم های پایه چه زمانی ، CNLJ ، CNLJ ، و الگوریتم های پایه به ترتیب ۲۸۱، ۴۷۱ و ۵۰۰۰ k پرس و جوهای FN را ارزیابی می کنند و بنابراین CNLJ الگوریتم ۱٫۲ و ۳۶٫۷ برابر سریعتر از CNLJ است و به ترتیب الگوریتم های پایه. شکل ۱۲ ب زمان های پردازش پرس و جو را نشان می دهد که تعداد نقاط داده از ۱۰۰۰ به ۵۰۰۰ تغییر می کند، به عنوان مثال، . صرف نظر از مقدار، CNLJ ، CNLJ ، و الگوریتم های پایه به ترتیب ۵۸، ۹۶ و ۱۰۰۰ k پرس و جوهای FN را ارزیابی می کنند. بنابراین، زمانی که ، CNLJ الگوریتم از CNLJ بهتر عمل می کند و الگوریتم های پایه به ترتیب ۱٫۲ و ۱۵٫۶ برابر. شکل ۱۲ c زمان های پردازش پرس و جو را نشان می دهد که تعداد FN های مورد نیاز بین ۱ و ۱۶ تغییر می کند، به عنوان مثال، . برای همه موارد در k ، CNLJ الگوریتم از CNLJ بهتر عمل می کند و الگوریتم های پایه به ترتیب ۱٫۲ و ۱۳٫۴ برابر. CNLJ ، CNLJ و زمان های پردازش پرس و جو الگوریتم های پایه تحت تأثیر مقدار k قرار نمی گیرند . این به این دلیل است که ارزیابی پرس و جو k FN فاصله یک نقطه پرس و جو تا خوشه های داده را بدون توجه به مقدار k محاسبه می کند و سپس خوشه های داده را با استفاده از فواصل تا نقطه پرس و جو مرتب می کند. شکل ۱۲ d زمان‌های پردازش پرس و جو را نشان می‌دهد که تعداد سانتروئیدها برای نقاط پرس و جو در Q بین ۱ تا ۱۰ تغییر می‌کند، به عنوان مثال، . به عنوان مقدار افزایش می یابد، تفاوت بین زمان پردازش پرس و جو همه الگوریتم ها کاهش می یابد. CNLJ الگوریتم ۱۳٫۳، ۱٫۳، ۱٫۶، ۱٫۷ و ۱٫۱ برابر سریعتر از الگوریتم پایه است که به ترتیب ۱، ۳، ۵، ۷ و ۱۰٫ دلیل آن این است که به عنوان مقدار افزایش می یابد، نقاط پرس و جو به طور گسترده ای پراکنده می شوند و تعداد خوشه های پرس و جو افزایش می یابد، و سرعت CNLJ را کاهش می دهد. زمان پردازش پرس و جو الگوریتم شکل ۱۲ e زمان‌های پردازش پرس و جو را نشان می‌دهد که تعداد سانتروئیدها برای نقاط داده در P بین ۱ تا ۱۰ تغییر می‌کند، به عنوان مثال، . زمان پردازش پرس و جو k FN با افزایش می یابد مقدار. این به این دلیل است که به عنوان مقدار افزایش می‌یابد، نقاط داده به طور گسترده پراکنده می‌شوند و تعداد خوشه‌های داده‌ای که باید با جست‌وجوهای k FN بررسی شوند نیز افزایش می‌یابد. به طور خلاصه، CNLJ الگوریتم از CNLJ بهتر عمل می کند و الگوریتم های پایه در همه موارد. این تایید می کند که CNLJ الگوریتم از خوشه بندی نقاط پرس و جوی نزدیک و بازیابی سریع نقاط داده کاندید در یک بار برای آن نقاط پرس و جو سود می برد.

در نقشه راه SJ، شکل ۱۳ عملکرد CNLJ را مقایسه می کند ، CNLJ و الگوریتم های پایه. توجه داشته باشید که نتایج تجربی با استفاده از نقشه راه SJ الگوهای عملکردی مشابهی را با آنهایی که از نقشه راه NA استفاده می کنند نشان می دهد. شکل ۱۳ a زمان های پردازش پرس و جو را نشان می دهد که . CNLJ الگوریتم ۱٫۲ و ۶٫۰ برابر سریعتر از CNLJ است و الگوریتم های پایه زمانی که ، به ترتیب. شکل ۱۳ ب زمان های پردازش پرس و جو را نشان می دهد که . CNLJ الگوریتم ۱٫۲ و ۴٫۵ برابر سریعتر از CNLJ است و الگوریتم های پایه زمانی که ، به ترتیب. را مقدار زمان پردازش پرس و جو را در همه الگوریتم ها افزایش می دهد. شکل ۱۳ ج زمان های پردازش پرس و جو را نشان می دهد که . CNLJ الگوریتم ۱٫۲ و ۳٫۵ برابر سریعتر از CNLJ است و به ترتیب الگوریتم های پایه. زمان پردازش پرس و جو بدون توجه به مقدار k تقریباً ثابت است. شکل ۱۳ d زمان های پردازش پرس و جو را نشان می دهد که . CNLJ الگوریتم ۳٫۵، ۲٫۴، ۱٫۸، ۱٫۴ و ۱٫۴ برابر سریعتر از الگوریتم پایه است که = به ترتیب ۱، ۳، ۵، ۷ و ۱۰٫ توزیع نقاط پرس و جو بر زمان پردازش پرس و جو CNLJ تأثیر دارد الگوریتم، همانطور که در این نتیجه نشان داده شده است. زمان پردازش پرس و جو CNLJ الگوریتم با تعداد خوشه های پرس و جو افزایش می یابد زیرا نقاط پرس و جو به طور گسترده پراکنده هستند. شکل ۱۳ e زمان های پردازش پرس و جو را نشان می دهد که . CNLJ الگوریتم ۲٫۸، ۴٫۰، ۳٫۵، ۲٫۹ و ۳٫۰ برابر سریعتر از الگوریتم پایه است که = به ترتیب ۱، ۳، ۵، ۷ و ۱۰٫

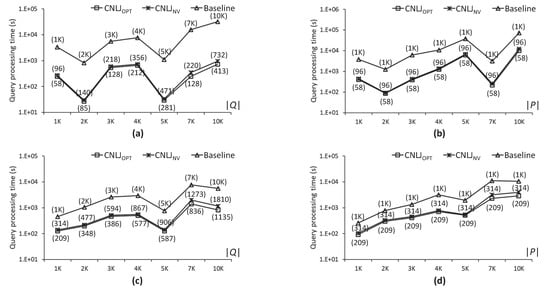
شکل ۱۴ عملکرد CNLJ را مقایسه می کند ، CNLJ و الگوریتم های پایه در حالی که تعداد نقاط پرس و جو و داده بین ۱۰۰۰ تا ۱۰۰۰۰ تغییر می کند، به عنوان مثال، و ، برای تأیید مقیاس پذیری CNLJ الگوریتم همانطور که در شکل ۱۴ a,c نشان داده شده است، CNLJ الگوریتم سریعتر از CNLJ اجرا می شود و الگوریتم های پایه برای همه موارد در . تفاوت عملکرد بین آنها معمولا با افزایش می یابد . به طور خاص، زمانی که ، CNLJ الگوریتم ۳۶٫۶ و ۵٫۳ برابر سریعتر از الگوریتم پایه برای نقشه های راه NA و SJ اجرا می شود. همانطور که در شکل ۱۴ نشان داده شده است ب، د، CNLJ نشان داده شده است الگوریتم سریعتر از CNLJ اجرا می شود و الگوریتم های پایه برای همه موارد در . به طور خاص، زمانی که ، CNLJ الگوریتم ۶٫۴ و ۳٫۰ برابر سریعتر از الگوریتم پایه برای نقشه های راه NA و SJ اجرا می شود. نتایج تجربی تایید می کند که CNLJ الگوریتم با هر دو مقیاس بهتری دارد و نسبت به CNLJ و الگوریتم های پایه

۶٫ بحث و نتیجه گیری

پرس و جو پیوستن k FN یک جفت از هر نقطه پرس و جو در Q را با k FN های آن در P بازیابی می کند ، با یک عدد صحیح k مثبت ، مجموعه ای از نقاط پرس و جو Q ، و مجموعه ای از نقاط داده P. پرس و جو پیوستن k FN کاربردهای واقعی مختلفی از جمله سیستم های توصیه گر و هندسه محاسباتی دارد [ ۶ ، ۷ ، ۸ ، ۹ ، ۱۰ ، ۱۱ ، ۱۲ ، ۱۳ ، ] . به طور خاص، پردازش کارآمد از kجستارهای پیوستن FN می تواند به انتخاب مکان تأسیساتی که دورترین مکان از امکانات ناخوشایند مانند زباله سوزها، کوره های آدم سوزی، و کارخانه های شیمیایی است کمک کند. یک الگوریتم اتصال حلقه تو در تو (CNLJ) در این مطالعه ساخته شد تا به طور موثر به k پیوستن FN بر روی نقاط پرس و جو که به طور یکنواخت در منطقه پراکنده شده اند پاسخ دهد. به جستارهای پیوستن k FN برای شبکه‌های فضایی ساخته شد. تا جایی که ما می دانیم، این اولین تلاش برای مطالعه kFN به پرس و جوها در شبکه های فضایی ملحق می شود. الگوریتم CNLJ نقاط پرس و جو (نقاط داده) را به خوشه های پرس و جو (خوشه های داده) تبدیل می کند. سپس نقاط داده کاندید را برای نقاط پرس و جوی خوشه ای به یکباره بازیابی می کند و نیاز به جستجوی نقاط داده کاندید برای هر نقطه پرس و جو را به طور جداگانه از بین می برد. با استفاده از نقشه‌های راه واقعی در شرایط مختلف، زمان‌های پردازش پرس و جو الگوریتم‌های پیوستن CNLJ و معمولی به صورت تجربی مقایسه شدند. نتایج تجربی نشان داد که الگوریتم CNLJ تا ۵۰٫۸ برابر سریع‌تر از الگوریتم‌های اتصال معمولی اجرا می‌شود و الگوریتم CNLJ نیز با تعداد داده‌ها و نقاط پرس و جو بهتر از الگوریتم‌های اتصال معمولی مقیاس می‌شود. متأسفانه، الگوریتم CNLJ عملکرد مشابهی با الگوریتم‌های اتصال مرسوم نشان می‌دهد. به ویژه هنگامی که نقاط پرس و جو به طور یکنواخت در منطقه قرار دارند. ما در نظر داریم راه حل پیشنهادی را در زمینه های مختلف در آینده اعمال کنیم. هنگامی که مجموعه داده در حافظه اصلی قرار نمی گیرد، ابتدا ساختارهای شاخص را در حافظه خارجی ایجاد می کنیم. دوم، ما یک مطالعه تجربی برای شبیه سازی سناریوهای زندگی واقعی با استفاده از مجموعه داده های واقعی انجام خواهیم داد. سوم، ما الگوریتم CNLJ را برای پردازش کارآمد بهبود خواهیم داد

منابع

گفت، ع. کیل، بی. جین، بی جی; Albayrak, S. افزایش تنوع از طریق دورترین توصیه مبتنی بر همسایه. در مجموعه مقالات کارگاه بین المللی تنوع در بازیابی اسناد، سیاتل، WA، ایالات متحده آمریکا، ۱۲ فوریه ۲۰۱۲; صص ۱-۴٫ [ Google Scholar ]
گفت، ع. فیلدز، بی. جین، بی جی; Albayrak، S. ارزیابی کاربر محور یک الگوریتم توصیه‌گر فیلتر مشارکتی k – دورترین همسایه. در مجموعه مقالات کنفرانس بین‌المللی کار تعاونی و محاسبات اجتماعی با پشتیبانی رایانه، سن آنتونیو، تگزاس، ایالات متحده آمریکا، ۲۳ تا ۲۷ فوریه ۲۰۱۳٫ صص ۱۳۹۹–۱۴۰۸٫ [ Google Scholar ]
وینمن، سی جی; Reinders، MJT; Backer, E. الگوریتم خوشه واریانس حداکثر. IEEE Trans. الگوی مقعدی ماخ هوشمند ۲۰۰۲ ، ۲۴ ، ۱۲۷۳-۱۲۸۰٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Defays, D. یک الگوریتم کارآمد برای یک روش پیوند کامل. محاسبه کنید. J. ۱۹۷۷ , ۲۰ , ۳۶۴-۳۶۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
واسيلوگلو، ن. گری، AG; اندرسون، DV یادگیری چندگانه نیمه معین مقیاس پذیر. در مجموعه مقالات کارگاه آموزشی IEEE در مورد یادگیری ماشین برای پردازش سیگنال، کانکون، مکزیک، ۱۶-۱۹ اکتبر ۲۰۰۸٫ صص ۳۶۸-۳۷۳٫ [ Google Scholar ]
کرتین، RR; اچائوز، ج. گاردنر، AB بهره برداری از ساختار جستجوی دورترین همسایه برای نتایج تقریبی سریع. Inf. سیستم ۲۰۱۹ ، ۸۰ ، ۱۲۴-۱۳۵٫ [ Google Scholar ] [ CrossRef ]
گائو، ی. شو، ال. چن، ک. Chen, G. جستارهای دورترین همسایه را روی داده های مکانی جمع کنید. در مجموعه مقالات کنفرانس بین المللی سیستم های پایگاه داده برای کاربردهای پیشرفته، هنگ کنگ، چین، ۲۲-۲۵ آوریل ۲۰۱۱٫ صص ۱۴۹-۱۶۳٫ [ Google Scholar ]
لیو، جی. چن، اچ. فیروس، ک. کیتاگاوا، H. یک الگوریتم کارآمد برای پرس و جوهای دلخواه معکوس دورترین همسایه. در مجموعه مقالات کنفرانس وب آسیا و اقیانوسیه در زمینه فناوری‌ها و برنامه‌های وب، کونمینگ، چین، ۱۱ تا ۱۳ آوریل ۲۰۱۲٫ صص ۶۰-۷۲٫ [ Google Scholar ]
لیو، دبلیو. یوان، ی. ایده های جدید برای جستارهای FN/RFN بر اساس نزدیکترین نمودار Voronoi. در مجموعه مقالات کنفرانس بین المللی محاسبات الهام گرفته از زیستی: نظریه ها و کاربردها، هوانگشان، چین، ۱۲ تا ۱۴ ژوئیه ۲۰۱۳٫ ص ۹۱۷-۹۲۷٫ [ Google Scholar ]
Tran، QT; تانیار، د. Safar، M. معکوس k نزدیکترین همسایه و معکوس دورترین همسایه در شبکه های فضایی. ترانس. داده های بزرگ مقیاس-دانش.-سنت. سیستم ۲۰۰۹ ، ۱ ، ۳۵۳-۳۷۲٫ [ Google Scholar ]
وانگ، اچ. ژنگ، ک. سو، اچ. وانگ، جی. صادق، جنوب; Zhou، X. پردازش پرس و جو از دورترین همسایه جمعی کارآمد در شبکه های جاده ای. در مجموعه مقالات کنفرانس پایگاه داده استرالیا در مورد نظریه و کاربردهای پایگاه های داده، بریزبن، استرالیا، ۱۴ تا ۱۶ ژوئیه ۲۰۱۴٫ صص ۱۳-۲۵٫ [ Google Scholar ]
شیائو، ی. لیو، بی. هائو، ز. کائو، L. رویکرد مبتنی بر دورترین همسایه برای توصیف داده‌های بردار پشتیبانی . Appl. هوشمند ۲۰۱۴ ، ۴۱ ، ۱۹۶-۲۱۱٫ [ Google Scholar ] [ CrossRef ]
خو، X.-J. بائو، J.-S. یائو، بی. ژو، J.-Y. تانگ، F.-L. Guo، M.-Y. خو، جی.-کیو. پرس و جوی دورترین همسایگان در شبکه های جاده ای را معکوس کنید. جی. کامپیوتر. علمی تکنولوژی ۲۰۱۷ ، ۳۲ ، ۱۵۵-۱۶۷٫ [ Google Scholar ] [ CrossRef ]
یائو، بی. لی، اف. Kumar، P. دورترین همسایگان را در پایگاه‌های داده فضایی معکوس کنید. در مجموعه مقالات کنفرانس بین المللی مهندسی داده، شانگهای، چین، ۲۹ مارس تا ۲ آوریل ۲۰۰۹٫ صص ۶۶۴-۶۷۵٫ [ Google Scholar ]
دوتا، بی. کارماکار، ا. روی، S. مشکل مکان یابی تسهیلات بهینه در زمین های چند وجهی با استفاده از مسیرهای نزولی. نظریه. محاسبه کنید. علمی ۲۰۲۰ ، ۸۴۷ ، ۶۸-۷۵٫ [ Google Scholar ] [ CrossRef ]
گائو، ایکس. پارک، سی. چن، ایکس. زی، ای. هوانگ، جی. ژانگ، دی. مکان های بهینه تاسیسات در سطح جهانی برای مشکلات مکان یابی تاسیسات در فضای پیوسته. Appl. علمی ۲۰۲۱ ، ۱۱ ، ۷۳۲۱٫ [ Google Scholar ] [ CrossRef ]
لیو، دبلیو. وانگ، اچ. ژانگ، ی. کین، ال. ژانگ، W. الگوریتم کارآمد I/O برای ج-تقریبی جستجوی دورترین همسایه در فضای با ابعاد بالا. در مجموعه مقالات کنفرانس بین المللی سیستم های پایگاه داده برای برنامه های پیشرفته، ججو، کره، ۲۴ تا ۲۷ سپتامبر ۲۰۲۰؛ ص ۲۲۱-۲۳۶٫ [ Google Scholar ]
هوانگ، Q. فنگ، جی. نیش، Q. Ng, W. دو طرح هش کارآمد برای جستجوی دورترین همسایه با ابعاد بالا. IEEE Trans. بدانید. مهندسی داده ۲۰۱۷ ، ۲۹ ، ۲۷۷۲-۲۷۸۵٫ [ Google Scholar ] [ CrossRef ]
لیو، ی. گونگ، ایکس. کنگ، دی. هائو، تی. Yan, X. یک گروه مبتنی بر Voronoi معکوس k روش جستجوی دورترین همسایه در فضای مانع. دسترسی IEEE ۲۰۲۰ ، ۸ ، ۵۰۶۵۹–۵۰۶۷۳٫ [ Google Scholar ] [ CrossRef ]
پاغ، ر. سیلوستری، اف. سیورتسن، جی. Skala، M. دورترین همسایه در ابعاد بالا. در مجموعه مقالات کنفرانس بین المللی جستجوی شباهت و کاربردها، گلاسکو، انگلستان، ۱۲ تا ۱۴ اکتبر ۲۰۱۵٫ صص ۳-۱۴٫ [ Google Scholar ]
کورن، اف. Muthukrishnan، S. مجموعه های نفوذ بر اساس پرس و جوهای معکوس نزدیکترین همسایه. در مجموعه مقالات کنفرانس بین المللی مدیریت داده ها، دالاس، تگزاس، ایالات متحده آمریکا، ۱۶-۱۸ می ۲۰۰۰٫ ص ۲۰۱-۲۱۲٫ [ Google Scholar ]
وانگ، اس. Cheema، MA; لین، ایکس. ژانگ، ی. لیو، دی. محاسبه کارآمد k دورترین همسایگان معکوس. در مجموعه مقالات کنفرانس بین المللی مهندسی داده، هلسینکی، فنلاند، ۱۶-۲۰ مه ۲۰۱۶٫ صص ۱۱۱۰–۱۱۲۱٫ [ Google Scholar ]
بکمن، ن. کریگل، اچ.-پی. اشنایدر، آر. Seeger, B. R*-tree: یک روش دسترسی کارآمد و قوی برای نقاط و مستطیل ها. در مجموعه مقالات کنفرانس بین المللی مدیریت داده ها، آتلانتیک سیتی، نیوجرسی، ایالات متحده آمریکا، ۲۳-۲۵ مه ۱۹۹۰٫ صص ۳۲۲-۳۳۱٫ [ Google Scholar ]
Guttman، A. R-trees: ساختار شاخص پویا برای جستجوی فضایی. در مجموعه مقالات کنفرانس بین المللی مدیریت داده ها، بوستون، MA، ایالات متحده آمریکا، ۱۸-۲۱ ژوئن ۱۹۸۴٫ ص ۴۷-۵۷٫ [ Google Scholar ]
هوانگ، Q. فنگ، جی. Fang, Q. درهم‌سازی حساس به موقعیت مکانی آگاهانه معکوس برای جستجوی دورترین همسایه با ابعاد بالا. در مجموعه مقالات کنفرانس بین المللی مهندسی داده، سن دیگو، کالیفرنیا، ایالات متحده آمریکا، ۱۹ تا ۲۲ آوریل ۲۰۱۷؛ صص ۱۶۷-۱۷۰٫ [ Google Scholar ]
لو، اچ. Yiu, ML در محاسبه دورترین مکان های تحت سلطه. IEEE Trans. بدانید. مهندسی داده ۲۰۱۱ ، ۲۳ ، ۹۲۸-۹۴۱٫ [ Google Scholar ] [ CrossRef ]
چو، اچ.-جی. پردازش اجرای مشترک کارآمد k- نزدیکترین همسایه در شبکه های جاده ای. اوباش Inf. سیستم ۲۰۱۸ ، ۲۰۱۸ ، ۵۵–۶۶٫ [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
او، دی. وانگ، اس. ژو، ایکس. Cheng, R. GLAD: یک چارچوب شبکه و برچسب‌گذاری با زمان‌بندی برای پرسش‌های knn آگاه از تعارض. IEEE Trans. بدانید. مهندسی داده ۲۰۲۱ ، ۳۳ ، ۱۵۵۴-۱۵۶۶٫ [ Google Scholar ] [ CrossRef ]
یانگ، آر. نیو، ب. جست‌وجوهای پیوسته نزدیک‌ترین همسایه بر روی جریان‌های داده‌های متنی-مکانی مقیاس بزرگ. ISPRS Int. J. Geo-Inf. ۲۰۲۰ ، ۹ ، ۶۹۴٫ [ Google Scholar ] [ CrossRef ]
چو، اچ.-جی. Attique، M. پردازش گروهی پرس و جوهای متعدد k- دورترین همسایه در شبکه های جاده ای. دسترسی IEEE ۲۰۲۰ ، ۸ ، ۱۱۰۹۵۹–۱۱۰۹۷۳٫ [ Google Scholar ] [ CrossRef ]
رضا، ر.م. علی، من هاشم، تی. پردازش گروهی پرس و جوهای کوتاه ترین مسیر همزمان در شبکه های جاده ای. در مجموعه مقالات کنفرانس بین المللی مدیریت داده های تلفن همراه، پیتسبورگ، PA، ایالات متحده آمریکا، ۱۵-۱۸ ژوئن ۲۰۱۵٫ صص ۱۲۸-۱۳۳٫ [ Google Scholar ]
ژانگ، ام. لی، ال. هوآ، دبلیو. ژو، ایکس. پردازش دسته ای کارآمد پرس و جوهای کوتاه ترین مسیر در شبکه های جاده ای. در مجموعه مقالات کنفرانس بین المللی مدیریت داده های تلفن همراه، هنگ کنگ، چین، ۱۰ تا ۱۳ ژوئن ۲۰۱۹؛ صص ۱۰۰-۱۰۵٫ [ Google Scholar ]
ژانگ، ام. لی، ال. هوآ، دبلیو. ژو، X. پردازش دسته‌ای از کوتاه‌ترین مسیرها در شبکه‌های جاده‌ای. در مجموعه مقالات کنفرانس پایگاه داده استرالیا در مورد نظریه و کاربردهای پایگاه داده، سیدنی، استرالیا، ۲۹ ژانویه تا ۱ فوریه ۲۰۱۹؛ صص ۳-۱۶٫ [ Google Scholar ]
رضا، ر.م. علی، من Cheema، MA مسیر و توقف های بهینه برای گروهی از کاربران در یک شبکه جاده ای. در مجموعه مقالات کنفرانس بین المللی پیشرفت در سیستم های اطلاعات جغرافیایی، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، ۷ تا ۱۰ نوامبر ۲۰۱۷؛ صص ۱-۱۰٫ [ Google Scholar ]
کیم، تی. چو، اچ.-جی. هنگ، اچ جی; نام، اچ. چو، اچ. انجام دهید، GY; Jeon, P. پردازش کارآمد k -دورترین همسایه پرس و جو برای شبکه های جاده ای. J. Korea Soc. محاسبه کنید. Inf. ۲۰۱۹ ، ۲۴ ، ۷۹–۸۹٫ [ Google Scholar ]
Abeywickrama، T. Cheema، MA; Taniar, D. k -نزدیکترین همسایگان در شبکه های جاده ای: سفری در آزمایش و پیاده سازی در حافظه. در مجموعه مقالات کنفرانس بین المللی پایگاه های داده بسیار بزرگ، دهلی نو، هند، ۵ تا ۹ سپتامبر ۲۰۱۶؛ صص ۴۹۲-۵۰۳٫ [ Google Scholar ]
لی، KCK; لی، W.-C. ژنگ، بی. Tian، Y. ROAD: یک چارچوب جدید جستجوی شی فضایی برای شبکه های جاده ای. IEEE Trans. بدانید. مهندسی داده ۲۰۱۲ ، ۲۴ ، ۵۴۷-۵۶۰٫ [ Google Scholar ] [ CrossRef ]
ژونگ، آر. لی، جی. تان، K.-L. ژو، ال. Gong, Z. G-tree: یک شاخص کارآمد و مقیاس پذیر برای جستجوی فضایی در شبکه های جاده ای. IEEE Trans. بدانید. مهندسی داده ۲۰۱۵ ، ۲۷ ، ۲۱۷۵-۲۱۸۹٫ [ Google Scholar ] [ CrossRef ]
کورمن، تی. Leiserson، CE; Rivest، RL; Stein, C. Introduction to Algorithms , ۳rd ed.; MIT Press and McGraw-Hill: Cambridge, MA, USA, 2009; صص ۶۴۳-۶۸۳٫ [ Google Scholar ]
مجموعه داده های واقعی برای پایگاه های داده فضایی. در دسترس آنلاین: https://www.cs.utah.edu/~lifeifei/SpatialDataset.htm (در ۴ اکتبر ۲۰۲۱ قابل دسترسی است).
وو، ال. شیائو، ایکس. دنگ، دی. کنگ، جی. زو، AD; ژو، اس. پرسش های کوتاه ترین مسیر و فاصله در شبکه های جاده ای: یک ارزیابی تجربی. در مجموعه مقالات کنفرانس بین المللی پایگاه های داده بسیار بزرگ، استانبول، ترکیه، ۲۷ تا ۳۱ اوت ۲۰۱۲٫ ص ۴۰۶-۴۱۷٫ [ Google Scholar ]
باست، اچ. فونکه، اس. Matijevic, D. Query های کوتاه ترین مسیر فوق سریع از طریق گره های حمل و نقل. در مجموعه مقالات کارگاه بین المللی در مورد مشکل کوتاه ترین مسیر، Piscataway، NJ، ایالات متحده، ۱۳-۱۴ نوامبر ۲۰۰۶٫ صص ۱۷۵-۱۹۲٫ [ Google Scholar ]
گیزبرگر، آر. سندرز، پی. شوتس، دی. Delling، D. سلسله مراتب انقباض: مسیریابی سلسله مراتبی سریعتر و ساده تر در شبکه های جاده ای. در مجموعه مقالات کارگاه بین المللی الگوریتم های تجربی، کیپ کد، MA، ایالات متحده آمریکا، ۳۰ مه تا ۲ ژوئن ۲۰۰۸٫ صص ۳۱۹-۳۳۳٫ [ Google Scholar ]
لی، ز. چن، ال. Wang, Y. G*-tree: یک شاخص فضایی کارآمد در شبکه های جاده ای. در مجموعه مقالات کنفرانس بین المللی مهندسی داده، ماکائو، چین، ۸ تا ۱۱ آوریل ۲۰۱۹؛ صص ۲۶۸-۲۷۹٫ [ Google Scholar ]
صامت، ح. سانکارانارایانان، ج. البرزی، ح. مرور از راه دور شبکه مقیاس پذیر در پایگاه داده های فضایی. در مجموعه مقالات کنفرانس بین المللی مدیریت داده ها، ونکوور، BC، کانادا، ۹-۱۲ ژوئن ۲۰۰۸٫ صص ۴۳-۵۴٫ [ Google Scholar ]

شکل ۱٫ مثالی از اتصال k FN ، جایی که و .

شکل ۲٫ مثالی از اتصال k FN در یک شبکه فضایی

شکل ۳٫ روش خوشه بندی دو مرحله ای برای گروه بندی نقاط پرس و جو در نزدیکی به خوشه های پرس و جو: ( الف ) تبدیل نقاط پرس و جو به بخش های پرس و جو. ( ب ) تبدیل بخش های پرس و جو به خوشه های پرس و جو.

شکل ۴٫ روش خوشه‌بندی دو مرحله‌ای برای گروه‌بندی نقاط داده نزدیک به یک خوشه داده: ( الف ) تبدیل نقاط داده به بخش‌های داده. ( ب ) تبدیل بخش های داده به خوشه های داده.